【算法基础】二分图（染色法 匈牙利算法）
相关文章：
【算法基础】二分图（染色法 匈牙利算法）
一、二分图 1. 染色法 一个图是二分图，当且仅当，图中不含奇数环。在判别一个图是否为二分图⑩，其实相当于染色问题，每条边的两个点必须是不同的颜色，一共有两种颜色，如果染色过程中出现矛盾，则说明不是二分图。 for i = 1 to n:if i 未染色DFS(i, 1); //将i号点染色未…...
Caputo 分数阶微分方程-慢扩散方程初边值问题基于L1 逼近的空间二阶方法及其Matlab程序实现
2.3.3 Caputo 分数阶一维问题基于 L1 逼近的空间二阶方法 考虑如下时间分数阶慢扩散方程初边值问题 { 0 C D t α u ( x , t ) = u...
 GPIO驱动)
I.MX6ULL_Linux_驱动篇(29) GPIO驱动
Linux 下的任何外设驱动，最终都是要配置相应的硬件寄存器。所以本篇的 LED 灯驱动最终也是对 I.MX6ULL 的 IO 口进行配置，与裸机实验不同的是，在 Linux 下编写驱动要符合 Linux 的驱动框架。I.MX6U-ALPHA 开发板上的 LED 连接到 I.MX6ULL 的 …...
jupyter的安装和使用
目录 ❤ Jupyter Notebook是什么？ notebook jupyter 简介 notebook jupyter 组成 网页应用 文档 主要特点 ❤ jupyter notebook的安装 notebook jupyter 安装有两种途径 1.通过Anaconda进行安装 2.通过pip进行安装 启动jupyter notebook ❤ jupyter …...
Springboot新手开发 Cloud篇
前言： 👏作者简介：我是笑霸final，一名热爱技术的在校学生。 📝个人主页：个人主页1 || 笑霸final的主页2 📕系列专栏：后端专栏 📧如果文章知识点有错误的地方，…...
Linux:函数指针做函数参数
#include <stdio.h> #include <stdlib.h> //创建带有函数指针做参数的函数框架api //调用者要先实现回调函数 //调用者再去调用函数框架 //所谓的回调是指 调用者去调用一个带有函数指针做参数的函数框架，函数框架反过来要调用调用者提供的回调函数 …...
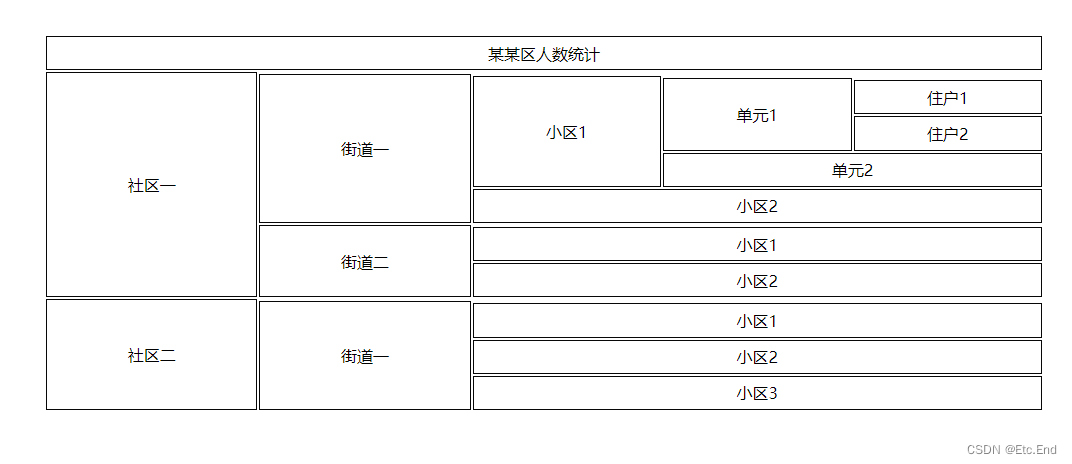
Vue3(递归组件) + 原生Table 实现树结构复杂表格
一、递归组件 什么是递归，Javascript中经常能接触到递归函数。也就是函数自己调用自己。那对于组件来说也是一样的逻辑。平时工作中见得最多应该就是菜单组件，大部分系统里面的都是递归组件。文章中我做了按需引入的配置，所以看不到我引用组…...
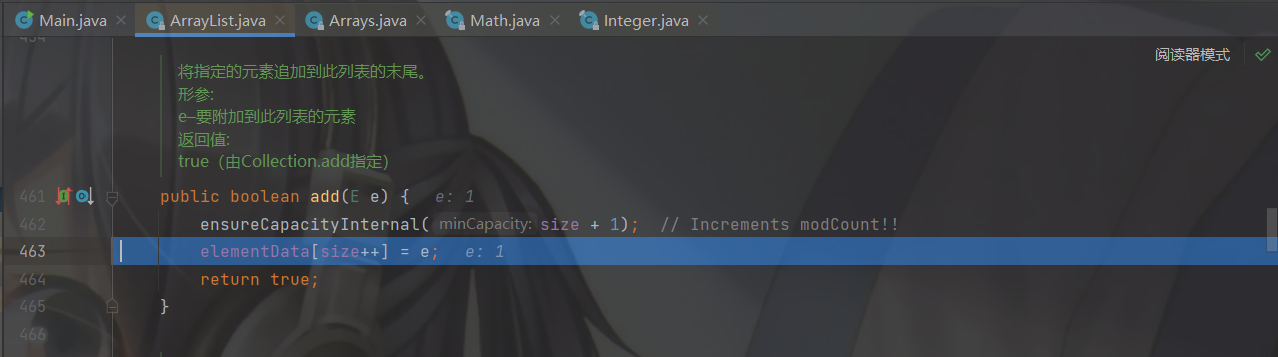
ArrayList底层源码解析
Java源码系列：下方连接 http://t.csdn.cn/Nwzed 文章目录前言一、**ArrayList底层结构和源码分析**无参构造调用创建ArrayList集合无参构造总结：发文3个工作日后 up 会把总结放入前言部分，但也诚邀读者总结，可放入评论区有参构造…...
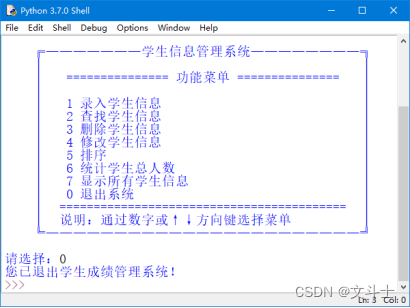
python：DIY字符画的程序使用说明.doc
目录开发环境要求运行方法具体的操作步骤如下：代码示例源码及运行程序下载地址开发环境要求 本系统的软件开发及运行环境具体如下。 操作系统：Windows 7、Windows 10。 Python版本：Python 3.7.0。 开发工具：Python IDLE。 …...
【Python/Opencv】图像权重加法函数：cv2.addWeighted()详解
【Python/Opencv】图像权重加法函数：cv2.addWeighted()详解 文章目录【Python/Opencv】图像权重加法函数：cv2.addWeighted()详解1. 介绍2. API3. 代码示例与效果3.1 代码3.2 效果4. 参考1. 介绍 在OpenCV图像加法cv2.add函数详解详细介绍了图像的加法运…...
容器的老祖宗LXC和Docker的关系
一、什么是LXC？ LXC（Linux Container的缩写）是一个基于Linux内核的容器虚拟化技术，它提供了一种轻量级、快速、简便的方式来创建和管理系统容器。与传统虚拟化技术不同，LXC并不会模拟硬件，而是利用Linux内…...
Webpack迁移Rspack速攻实战教程（前瞻版）
前言 rspack 即将开源，但社区中不乏有已经落地的 case ，比如 rspack-migration-showcase 、 modern.js 等。 基于此，本文将介绍如何迁移一个近似于 CRA（ create-react-app ） 的项目到 rspack 。 在阅读本文前&#…...
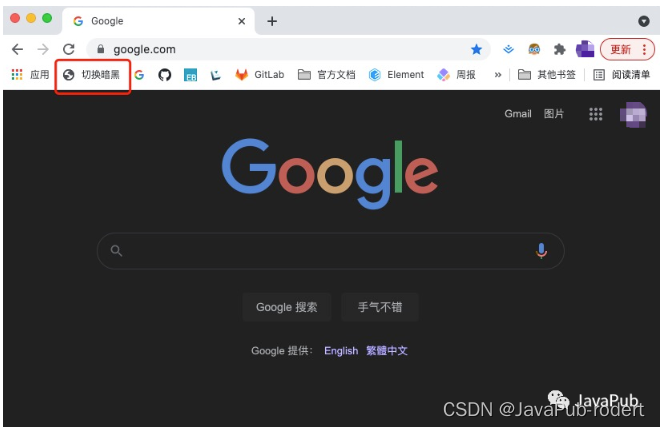
一行代码“黑”掉任意网站
文章目录只需一行代码，轻轻一点就可以把任意网站变成暗黑模式。 首先我们先做一个实验，在任意网站中，打开浏览器开发者工具(F12)，在 C1onsole 控制台输入如下代码并回车： document.documentElement.style.filterinve…...
51单片机入门 -驱动 8x8 LED 点阵屏
硬件型号、软件版本、以及烧录流程 操作系统：Windows 10 x84-64单片机：STC89C52RC编译器：SDCC烧录软件：stcgal 1.6开发板：普中51单片机开发板A2套件（2022） 在 VS Code 中新建项目到烧录的过程…...
Xinlinx zynq7045国产替代 FMQL45T900全国产化 ARM 核心板+扩展板
TES745D 是一款基于 FMQL45T900 的全国产化 ARM 核心板。该核心板将 FMQL45T900（与XC7Z045-2FFG900I 兼容）的最小系统集成在了一个 87*117mm 的核心板上，可以作为一个核心模块，进行功能性扩展，能够快速的搭建起一个信号…...
硬刚ChatGPT！文心一言能否为百度止颓？中国版ChatGPT“狂飙”的机会在哪儿？
文章目录目录产品背景发展历程科技简介主要功能合作伙伴结语文心一言 （英文名：ERNIE Bot） *是百度基于文心大模型技术推出的生成式对话产品，被外界誉为“中国版ChatGPT”，将于2023年3月份面向公众开放。 [40] 百度在人…...
Python 异步: 在非阻塞子进程中运行命令（19）
动动发财的小手，点个赞吧！ 我们可以从 asyncio 执行命令。该命令将在我们可以使用非阻塞 I/O 写入和读取的子进程中运行。 1. 什么是 asyncio.subprocess.Process asyncio.subprocess.Process 类提供了由 asyncio 运行的子进程的表示。它在 asyncio 程序…...
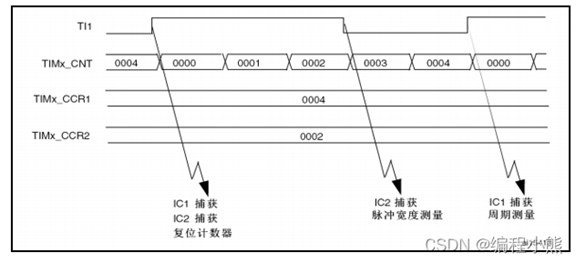
蓝桥杯嵌入式第五课--输入捕获
前言输入捕获的考题十分明确，就是测量输入脉冲波形的占空比和频率，对我们的板子而言，就是检测板载的两个信号发生器产生的信号：具体来说就是使用PA15和PB4来做输入捕获。输入捕获原理简介输入捕获能够对输入信号的上升沿和下降沿进…...
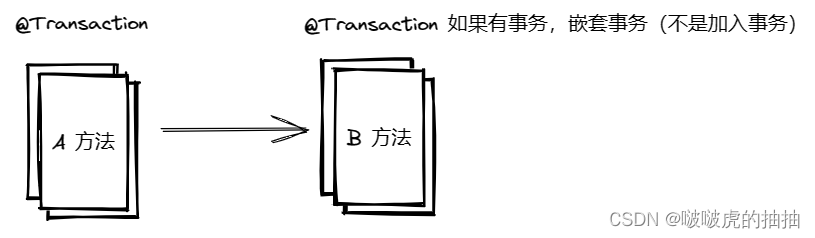
Spring事务和事务传播机制
目录 Spring中事务的实现 1、通过代码的方式手动实现事务 2、通过注解的方式实现声明式事务 2.1、Transactional作用范围 2.2、Transactional参数说明 2.3、注意事项 2.4、Transactional工作原理 事务隔离级别 1、事务特性 2、Spring中设置事务隔离级别 2.1、MySQL事…...
基于OpenCV+CUDA实时视频抠绿、背景合成以及抠绿算法小结
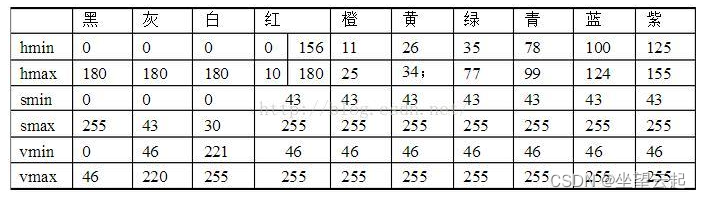
一、关于抠绿 百度百科上描述抠绿“抠绿是指在摄影或摄像时，以绿色为背景进行拍摄，在后期制作时使用特技机的“色键”将绿色背景抠去，改换其他更理想的背景的技术。”绿幕的使用已经非常普遍，大到好莱坞大片，小到自媒体的节目，一些商业娱乐场景，几乎都用使用。但是很多非…...
【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道（多模态 OCR → 语义检索 → 答案渲染）、两级检索（倒排 BM25 向量 HNSW）并以大语言模型兜底”的整体框架： 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后，分别用…...
Cursor实现用excel数据填充word模版的方法
cursor主页：https://www.cursor.com/ 任务目标：把excel格式的数据里的单元格，按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例，…...
ES6从入门到精通：前言
ES6简介 ES6（ECMAScript 2015）是JavaScript语言的重大更新，引入了许多新特性，包括语法糖、新数据类型、模块化支持等，显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用，可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器，能够帮助开发者更好地管理复杂的依赖关系，而 GraphQL 则是一种用于 API 的查询语言，能够提…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
macOS多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台（Launchpad）多出来了：Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显，都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
【AI学习】三、AI算法中的向量
在人工智能（AI）算法中，向量（Vector）是一种将现实世界中的数据（如图像、文本、音频等）转化为计算机可处理的数值型特征表示的工具。它是连接人类认知（如语义、视觉特征）与…...
【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例，模拟20个网页的爬取，每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程：允许程序同时执行多个任务，提高IO密集型任务（如网络请求）的效率…...
Device Mapper 机制
Device Mapper 机制详解 Device Mapper（简称 DM）是 Linux 内核中的一套通用块设备映射框架，为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程，并配以详细的…...
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...