算法小抄6-二分查找
二分查找,又名折半查找,其搜索过程如下:
- 从数组中间的元素开始,如果元素刚好是要查找的元素,则搜索过程结束
- 如果搜索元素大于或小于中间元素,则排除掉不符合条件的那一半元素,在剩下的数组中进行查找
- 由于每次需要排除掉一半不符合要求的元素,这需要数组是已经排好序的或者是有规律可循的
在二分查找中,对于每一个反馈,我们能过滤掉一半的数据,因此二分查找相对于普通遍历是一个高效的查找算法,其时间复杂度为O(logn),虽然二分查找的思想很简单,然而二分查找的细节可不少,这里根据力扣的题型给出两种二分查找的写法
二分查找基础版

题目链接
使用二分查找的方式在一个升序的数组中找到指定的值并且返回,其代码框架如下:
定义left为左指针,right为右指针,搜索的区域在[left,right]中
搜索目标值为targtwhile(left<=right){//得到查找的中点mid=(left+right)/2//对于升序数组当前值小于目标值,目标值应该在当前值的右侧if(mid<target){左指针右移,如今搜索区域变为[mid,right]}else if(mid>target){右指针左移,如今搜索区域变为[left,mid]}else{只剩下等于的情况了,直接返回结果找到了目标值}
}
代码如下:
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:mid = (right - left) // 2 + leftnum = nums[mid]if num < target:left = mid + 1elif num > target:right = mid - 1else:return midreturn -1注意,重点来了!!!注意代码中的几个关键点:
- while循环中的条件是left<=right,这意味着在搜索不到答案退出循环时left=right+1,而在二分查找中我们查找的是[left,right]这个区间,这说明所有的数都被搜索到了,记住这一点,以下我们统称left<=right的这种写法为写法一
- mid=(right-left)//2+left这个写法其实与mid=(left+right)/2效果是一致的,这么写的目的是为了防止整形溢出的情况,因为left+right相加如果大于整形最大值的话会导致结果异常
- 在移动左右指针时使用的是right=mid-1和left=mid+1,这是因为mid的值已经在上一轮循环中搜索过了,不需要再进行一次搜索
二分查找进阶版--寻找左右边界
为了引出二分查找的第二种写法,这里给出一道非力扣题型的二分查找
寻找左侧边界
例如对于数组[1,2,2,2,3],查找目标为2,我们需要返回最左边的2的下标1,如果使用写法一我们的代码看起来是下面这样的:
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:mid = (right - left) // 2 + leftnum = nums[mid]if num < target:left = mid + 1elif num > target:right = mid - 1else:right = mid - 1if(left >= len(nums) || nums[left] != target): return -1return left这段代码有两个注意点:
- 由于要找到最左侧的边界,在else条件里(num=target), 我们不再直接返回结果,而是继续的收缩右边界,直到right越界或者找到最左边界坐标
- 是不是决定很奇怪,为什么最后返回的是left,而且是对left做越界判定,记不记得我在之前说过left<=right的退出条件是left=right+1,我们复盘一下最后一轮循环的情况,你就知道为什么最后返回的是left而且也是对left进行越界的判断了
- 复盘最后一轮循环的过程,对于数组[1,2,2,2,3],target为2,假设当前mid为1,循环也接近了极限,也就是left=mid=right=1,根据代码,在num=target=2的时候,根据代码right=mid-1,那么最后right是否一定不指向正确的结果1,而left指针还没有被移动,依然指向mid,所以我们最后应该返回left
- 再来看一种情况对于数组[1,2,2,2,3]如果我们查找的是数字4,由于数组中的数字都小于target,我们会不断的缩小左边界,直到退出循环left=right+1,此时left一定是越界的,因为right从头到尾都没动过,而left=right+1保证了left越界
- 再来看一种情况对于数组[1,2,2,2,3]如果查找的是数字0,由于数组中的数字都大于target,我们会不断的缩小右边界,直到退出循环left=right+1,由于我们最后判断的是left指针,即使right指针越界了,left=right+1也能保证left刚好在下标0的位置,所以是不需要考虑左侧越界的情况的
讲到这里是不是觉得写法一来解决这样的问题真的很复杂,所以我们接下来要说写法二
写法二
使用写法二来解决左侧边界问题,代码如下:
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left < right:mid = (right - left) // 2 + leftnum = nums[mid]if num < target:left = mid + 1else:right = midreturn left注意点如下:
- while循环结束的条件是left<right,这说明循环退出的条件是left==right==mid,最后的返回值我们这里返回的是left,其实返回right也是可以的,因为循环退出的条件是left==mid==right嘛
- 可以看到另一个不同在于在else条件里我们偏移右指针的时候写的是right=mid,我们合并了num>target和num=target的条件,所以为什么是写成right=mid而不是right=mid-1呢?
left=mid+1和right=mid
- 对于left=mid+1可以这么理解,mid此时的值一定不是我们需要的值,所以我们可以直接越过.举个例子对于数组[1,2,3,4,4,5,5],如果要搜索数字5,我们第一个搜索到的数字mid=(left+right)/2=nums[3]=4,此时4<target,那么是否一定不是我们需要的结果,那么我们可以直接越过
- 对于right=mid,mid的值可能是我们需要的值,但是在当前循环中我们无法判断出来,所以我们进行保留,举个列子,对于数组[1,5,5,5],如果要搜索数字5,我们第一个搜索到的数字mid=nums[1]=5,此时的5是下标为1的5,并且也是最终我们需要找到的最左侧边界,此时right=mid这行代码就能帮助我们把结果保留了,而后等待left不断右移知道left==right就能退出循环返回最终结果了
寻找右侧边界
学会了寻找左侧边界,那么右侧边界是否也很容易理解了,其实这里有一个小坑,还需要填一下,这里先给出寻找右侧边界的代码
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left < right:mid = (right - left + 1) // 2 + leftnum = nums[mid]if num > target:right = mid - 1else:left = midreturn right
- 相信你已经发现了,在取mid的时候我们在括号里加上了一个1,这是因为程序语言中除法操作后下标向下取整(例如(1+2)/2=1),而在寻找右侧边界的过程中,这个操作会导致死循环,永远退不出循环,举个列子:
- 两者相除,向下取整,这个操作是不是说明mid在有些情况下会向左偏向,我们在寻找左侧边界的时候,需要它向左偏向因此能退出循环,而在寻找右侧边界时,需要它向右收缩边界,此时是否就和向下取整这个情况矛盾了,此时一左一右就会导致永远进入死循环了,因此需要mid=(right-left+1)//2+left这个操作来打破这个死循环
总结
这里很重要哦,如果理解了这里,就离彻底理解二分写法不远了
- 写法一适合用于在[left,right]这个范围内找到值,例如最基础的二分写法,这种写法需要判断最后返回的是left还是right,要分析最后一次循环后造成的结果
- 写法二适合用于在[left,right]这个区间内排除值,然后在left=right=mid的时候找到最后的答案,因此写法二的if条件里写的是target值一定不存在的情况
- 在写法二中如果else条件里是left=mid这个条件(趋向是收缩左边界和向下取整相反),需要修改mid为(right-left+1)//2+left来避免死循环情况的出现
二分搜索代码很简单,但细节是魔鬼,如果觉得自己理解了可以使用写法二做做这一题,题目链接
相关文章:

算法小抄6-二分查找
二分查找,又名折半查找,其搜索过程如下: 从数组中间的元素开始,如果元素刚好是要查找的元素,则搜索过程结束如果搜索元素大于或小于中间元素,则排除掉不符合条件的那一半元素,在剩下的数组中进行查找由于每次需要排除掉一半不符合要求的元素,这需要数组是已经排好序的或者是有…...
大学四年..就混了毕业证的我,出社会深感无力..辞去工作,从头开始
时间如白驹过隙,一恍就到了2023年,今天最于我来说是一个值得纪念的日子,因为我收获了今年的第一个offer背景18年毕业,二本。大学四年,也就将就混了毕业证和学位证。毕业后,并未想过留在湖南,就回…...

C语言数据结构初阶(6)----链表常见OJ题
CSDN的uu们,大家好!编程能力的提高不仅需要学习新的知识,还需要大量的练习。所以,C语言数据结构初阶的第六讲邀请uu们一起来看看链表的常见oj题目。移除链表元素原题链接:203. 移除链表元素 - 力扣(Leetcod…...

关键字 const
目录 一、符号常量与常变量 二、const的用法 2.1 const常用方法 2.2 const用于指针 2.2.1 p指针所指的对象值不能改变,但是p指针的指向可以改变 2.2.2 常指针p的指向不能改变,但是所指的对象的值可以改变 2.2.3 p所指对象的指向以及对象的值都不可…...
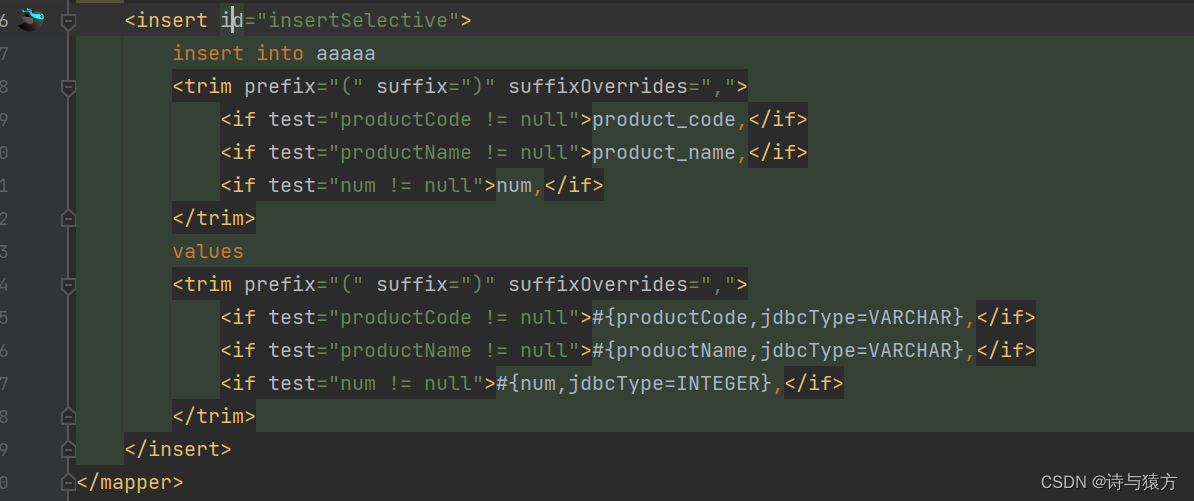
MybatisPlus------MyBatisX插件:快速生成代码以及快速生成CRUD(十二)
MybatisPlus------MyBatisX插件(十二) MyBatisX插件是IDEA插件,如果想要使用它,那么首先需要在IDEA中进行安装。 安装插件 搜索"MyBatisX",点击Install,之后重启IDEA即可。 插件基本用途&…...
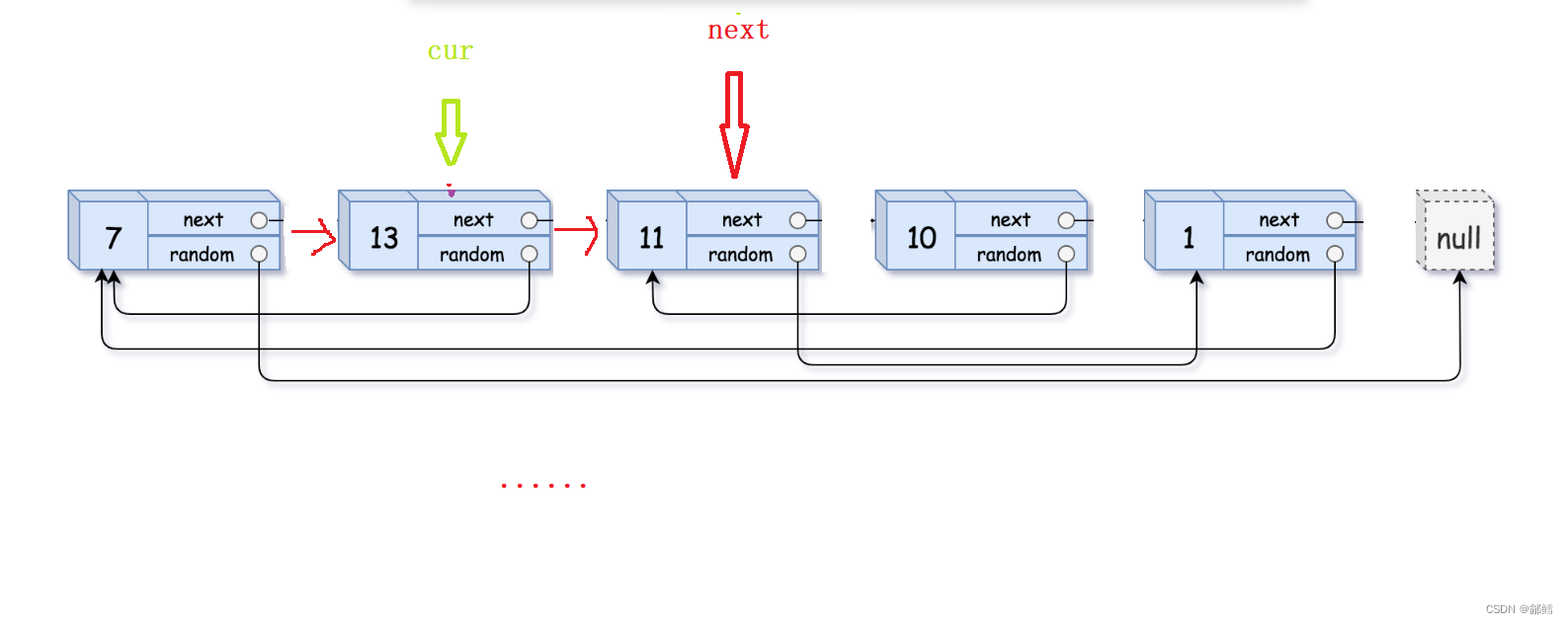
Leetcode138. 复制带随机指针的链表
复制带随机指针的链表 第一步 拷贝节点链接在原节点的后面 第二步拷贝原节点的random , 拷贝节点的 random 在原节点 random 的 next 第三步 将拷贝的节点尾插到一个新链表 ,并且将原链表恢复 从前往后遍历链表 ,将原链表的每个节点进行复制,并l链接到原…...
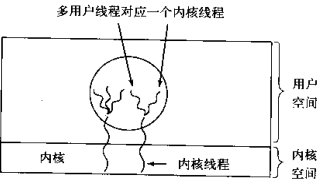
python并发编程多线程
在传统操作系统中,每个进程有一个地址空间,而且默认就有一个控制线程 线程顾名思义,就是一条流水线工作的过程,一条流水线必须属于一个车间,一个车间的工作过程是一个进程 车间负责把资源整合到一起,是一个…...

使用Maven实现Servlet程序
创建Maven项目我们打开idea的新建项目,选中里面Maven即可,如下图:创建完成之后,会看到这样的目录结构其中,main目录存放业务代码,其中的java目录存放的就是java代码,而resources目录存放是程序中依赖的文件,比如:图片,视频等.然后是 test目录,test目录存放的是测试代码.最后一个…...
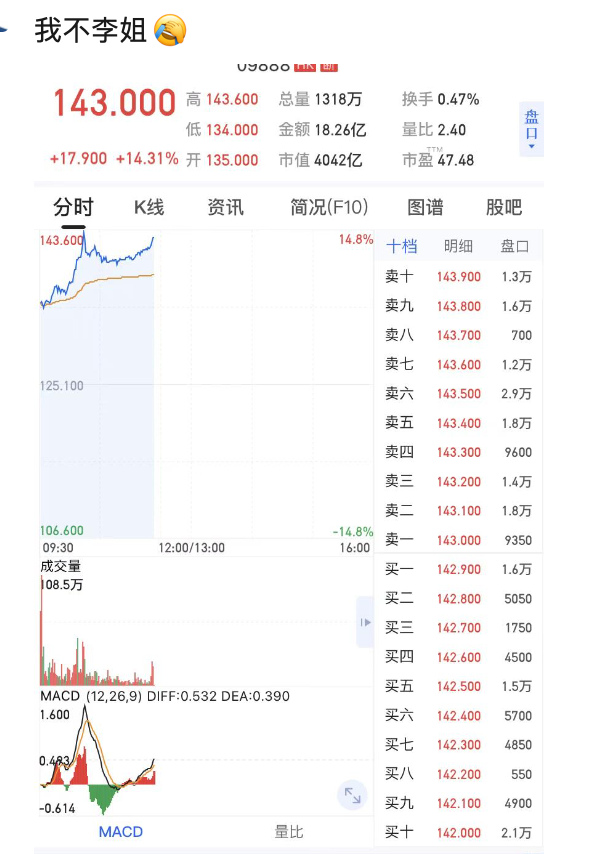
百度的文心一言 ,没有想像中那么差
robin 的演示 我们用 robin 的演示例子来对比一下 文心一言和 ChatGPT 的真实表现(毕竟发布会上是录的)。 注意,我使用的 GPT 版本是 4.0 文学创作 1 三体的作者是哪里人? 文心一言: ChatGPT: 嗯&a…...

文心一言发布的个人看法
文心一言发布宣传视频按照发布会上说的,文心一言并非属于百度赶工抄袭Chat-GPT的作品,而是十几年一直布局AI产业厚积薄发的成果,百度在芯片,机器学习,自然语言处理,知识图谱等方面均有相对深厚的积累。 国…...

【C5】111
文章目录bmc_wtd:syscpld.c中wd_en和wd_kick节点对应寄存器,crontab,FUNCNAMEAST2500/2600 WDT切换主备:BMC用WDT2作为主备切换的watchdog控制器AC后读取:bmc处于主primary flash(设完后:实际主…...

静态成员,友元函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
:函数)
数学分析课程笔记(张平):函数
01 函数 \quad作为数学分析的第一节课,首先深入了解一下函数。 \quad翻看一些教材可以发现,有些教材将“函数”与“映射”区分为两个概念,有些教材(尤其是前苏联时期的一些教材)则将其视为一个概念。实际上,…...

spring事务 只读此文
文章目录一. 事务概述1.1. MySQL 数据库事务1.2 spring的事务支持:1.2.1 编程式事务:1.2.2 声明式事务1.2.3 事务传播行为:1.2.4 事务隔离级别1.2.5 事务的超时时间1.2.6 事务的只读属性1.2.7 事务的回滚策略二. spring事务(注解 Transaction…...
真实的软件测试日常工作是咋样的?
最近很多粉丝问我,小姐姐,现在大环境不景气,传统行业不好做了,想转行软件测试,想知道软件测试日常工作是咋样的?平常的工作内容是什么? 别急,今天跟大家细细说一下一个合格的软件测…...
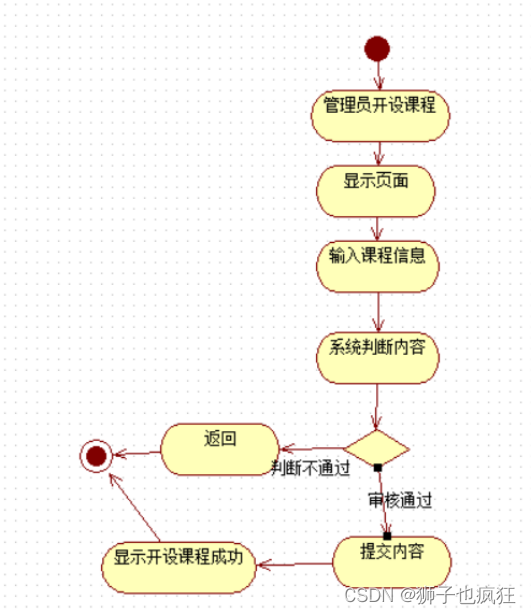
【UML】软件需求说明书
目录🦁 故事的开端一. 🦁 引言1.1编写目的1.2背景1.3定义1.4参考资料二. 🦁 任务概述2.1目标2.2用户的特点2.3假定和约束三. 🦁 需求规定3.1 功能性需求3.1.1系统用例图3.1.2用户登录用例3.1.3学员注册用例3.1.4 学员修改个人信息…...

面试官:html里面哪个元素可以让文字换行展示
在HTML中,可以使用 <br> 元素来强制换行,也可以使用CSS的 word-break 或 white-space 属性来实现自动换行。以下是这些方法的具体说明: 1.使用 <br> 元素 <br> 元素可以在文本中插入一个换行符,使文本从该位置…...

XGBoost和LightGBM时间序列预测对比
XGBoost和LightGBM都是目前非常流行的基于决策树的机器学习模型,它们都有着高效的性能表现,但是在某些情况下,它们也有着不同的特点。 XGBoost和LightGBM简单对比 训练速度 LightGBM相较于xgboost在训练速度方面有明显的优势。这是因为Ligh…...
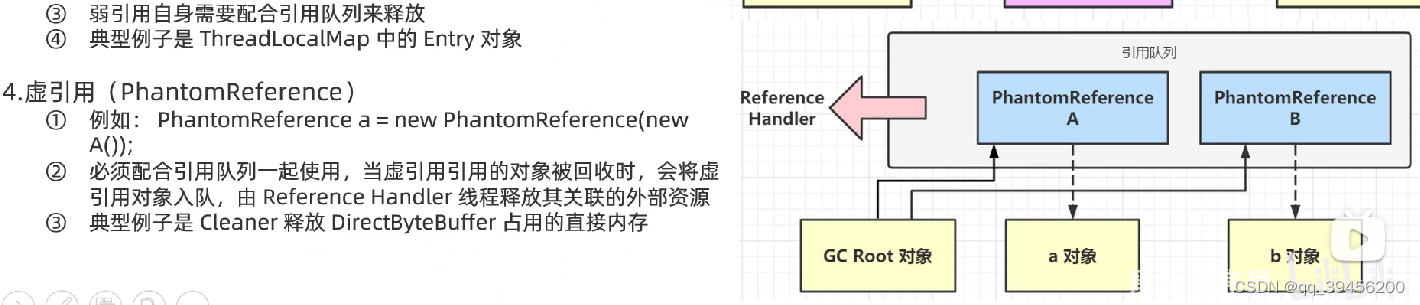
JVM高频面试题
1、项目中什么情况下会内存溢出,怎么解决? (1)误用固定大小线程池导致内存溢出 Excutors.newFixedThreadPool内最大线程数是21亿(2) 误用带缓冲线程池导致内存溢出最大线程数是21亿(3)一次查询太多的数据,导致内存占用…...
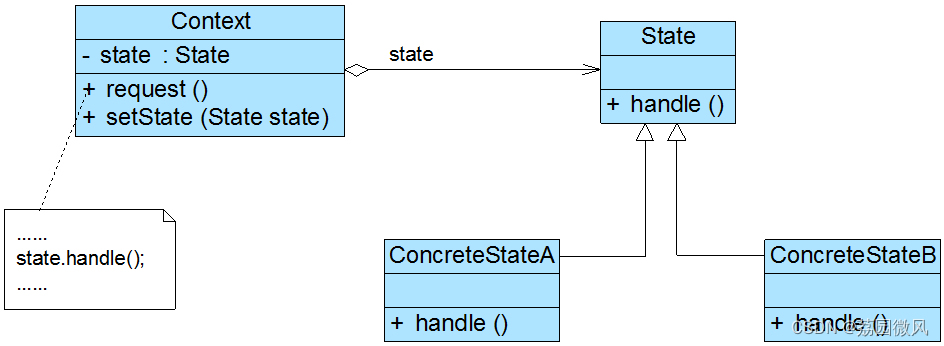
Windows环境下实现设计模式——状态模式(JAVA版)
我是荔园微风,作为一名在IT界整整25年的老兵,今天总结一下Windows环境下如何编程实现状态模式(设计模式)。不知道大家有没有这样的感觉,看了一大堆编程和设计模式的书,却还是很难理解设计模式,无…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
