数学分析课程笔记(张平):函数
01 函数
\quad 作为数学分析的第一节课,首先深入了解一下函数。
\quad 翻看一些教材可以发现,有些教材将“函数”与“映射”区分为两个概念,有些教材(尤其是前苏联时期的一些教材)则将其视为一个概念。实际上,“函数”也的确就是“映射”。
\quad 在高中阶段,我们认为函数的概念为:若给定集合 X,YX,YX,Y,存在一个对应法则 fff,使得
∀x∈X,∃!y∈Ys.t.y=f(x),\forall ~ x \in X,~\exists ~ !y \in Y \quad s.t.\quad y=f(x), ∀ x∈X, ∃ !y∈Ys.t.y=f(x),
则称 f:X⟶Yf:X\longrightarrow Yf:X⟶Y 为 函数。简单来说,函数可以是“一对一”,亦可以是“多对一”,但绝不可以是“一对多”!
\quad 步入分析学的领域后,函数的概念需要进行拓广!
函数:若给定集合 X,YX,YX,Y,存在一个对应法则 fff,使得
∀x∈X,∃y∈Ys.t.y=f(x),\forall ~ x \in X,~\exists ~ y \in Y \quad s.t.\quad y=f(x), ∀ x∈X, ∃ y∈Ys.t.y=f(x),
则称 f:X⟶Yf:X\longrightarrow Yf:X⟶Y 为 函数。进行拓广后,函数也可以是“一对多”了。
\quad 复变函数就是典型的“一对多”函数。
\quad 设 f:X⟶Yf:X\longrightarrow Yf:X⟶Y 为函数,即:
X→fY∀x∈X↦y∈Y,y=f(x)\begin{aligned} X &\xrightarrow{f}Y \\ \forall x\in X &\mapsto y\in Y,y=f\left( x \right) \end{aligned} X∀x∈XfY↦y∈Y,y=f(x)
则:
f(X):={y∈Y∣∃x((x∈X)∧(y=f(x)))}f(X):=\{y \in Y\mid \exists ~ x ((x \in X)\land(y=f(x)))\} f(X):={y∈Y∣∃ x((x∈X)∧(y=f(x)))}
称为函数的 值域。
\quad 其中,XXX 称为 定义域,YYY 称为 到达域。
\quad 显然,定义一个函数(或者说是映射),需要知晓:
- 定义域 XXX;
- 对应法则 fff;
- 到达域 YYY.
\quad 微积分主要研究的是 可微函数,实变函数主要研究 可测函数。通常我们研究的函数形式为 f:X⟶Yf:X \longrightarrow Yf:X⟶Y,X,Y⊂RnX,Y \subset \mathbb{R}^{n}X,Y⊂Rn. 而研究这种函数,首先就要先认识 Rn\mathbb{R}^{n}Rn 或者 R\mathbb{R}R.
\quad R\mathbb{R}R 是什么东西?中学我们便接触它了,它就是 实数集。但实际上,正如我们会使用计算机,但不清楚其构造原理一般,我们缺乏对实数集 R\mathbb{R}R 的真正认识!
参考:
- 张平. 数学分析课程.
相关文章:
:函数)
数学分析课程笔记(张平):函数
01 函数 \quad作为数学分析的第一节课,首先深入了解一下函数。 \quad翻看一些教材可以发现,有些教材将“函数”与“映射”区分为两个概念,有些教材(尤其是前苏联时期的一些教材)则将其视为一个概念。实际上,…...

spring事务 只读此文
文章目录一. 事务概述1.1. MySQL 数据库事务1.2 spring的事务支持:1.2.1 编程式事务:1.2.2 声明式事务1.2.3 事务传播行为:1.2.4 事务隔离级别1.2.5 事务的超时时间1.2.6 事务的只读属性1.2.7 事务的回滚策略二. spring事务(注解 Transaction…...
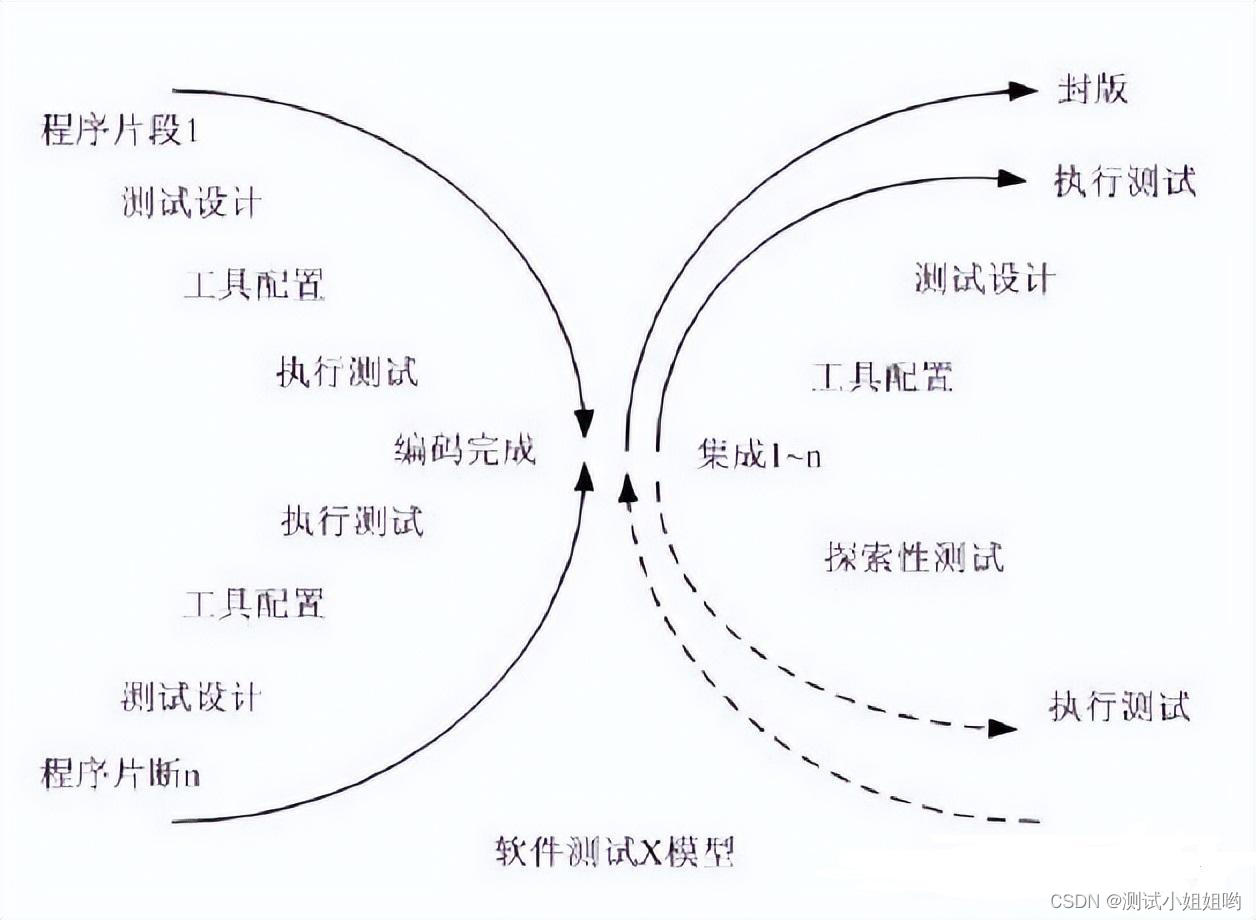
真实的软件测试日常工作是咋样的?
最近很多粉丝问我,小姐姐,现在大环境不景气,传统行业不好做了,想转行软件测试,想知道软件测试日常工作是咋样的?平常的工作内容是什么? 别急,今天跟大家细细说一下一个合格的软件测…...
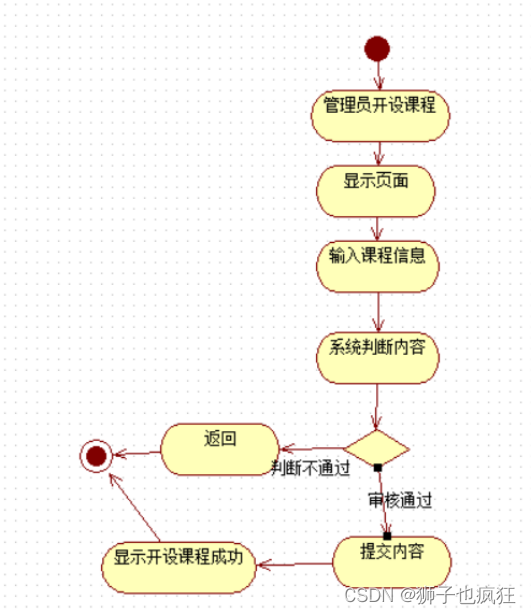
【UML】软件需求说明书
目录🦁 故事的开端一. 🦁 引言1.1编写目的1.2背景1.3定义1.4参考资料二. 🦁 任务概述2.1目标2.2用户的特点2.3假定和约束三. 🦁 需求规定3.1 功能性需求3.1.1系统用例图3.1.2用户登录用例3.1.3学员注册用例3.1.4 学员修改个人信息…...

面试官:html里面哪个元素可以让文字换行展示
在HTML中,可以使用 <br> 元素来强制换行,也可以使用CSS的 word-break 或 white-space 属性来实现自动换行。以下是这些方法的具体说明: 1.使用 <br> 元素 <br> 元素可以在文本中插入一个换行符,使文本从该位置…...

XGBoost和LightGBM时间序列预测对比
XGBoost和LightGBM都是目前非常流行的基于决策树的机器学习模型,它们都有着高效的性能表现,但是在某些情况下,它们也有着不同的特点。 XGBoost和LightGBM简单对比 训练速度 LightGBM相较于xgboost在训练速度方面有明显的优势。这是因为Ligh…...
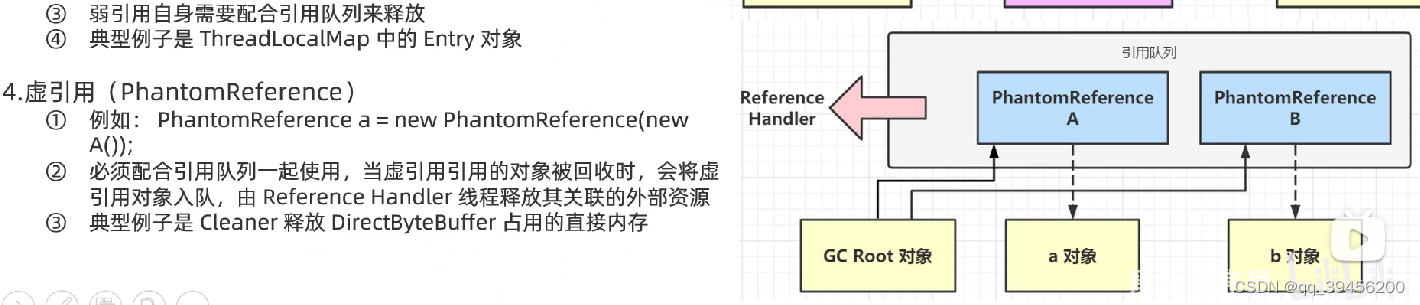
JVM高频面试题
1、项目中什么情况下会内存溢出,怎么解决? (1)误用固定大小线程池导致内存溢出 Excutors.newFixedThreadPool内最大线程数是21亿(2) 误用带缓冲线程池导致内存溢出最大线程数是21亿(3)一次查询太多的数据,导致内存占用…...
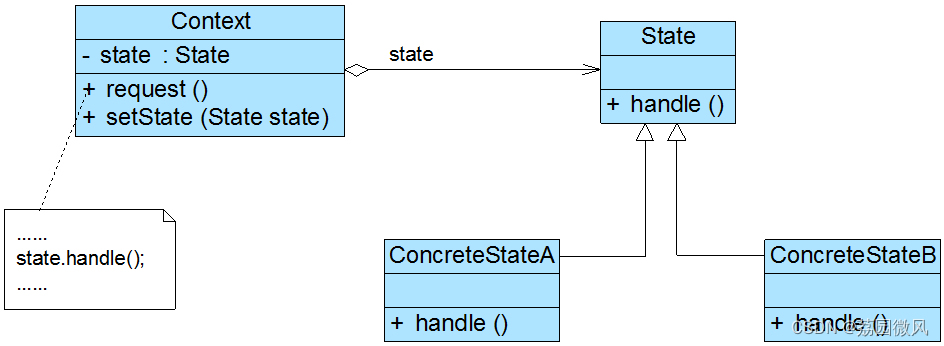
Windows环境下实现设计模式——状态模式(JAVA版)
我是荔园微风,作为一名在IT界整整25年的老兵,今天总结一下Windows环境下如何编程实现状态模式(设计模式)。不知道大家有没有这样的感觉,看了一大堆编程和设计模式的书,却还是很难理解设计模式,无…...
)
【总结】多个条件排序(pii/struct/bool)
目录 pii struct bool pii 现在小龙同学要吃掉它们,已知他有n颗苹果,并且打算每天吃一个。 但是古人云,早上金苹果,晚上毒苹果。由此可见,早上吃苹果和晚上吃苹果的效果是不一样的。 已知小龙同学在第 i 天早上吃苹果能…...
基于stm32mp157 linux开发板ARM裸机开发教程Cortex-A7 开发环境搭建(连载中)
前言:目前针对ARM Cortex-A7裸机开发文档及视频进行了二次升级持续更新中,使其内容更加丰富,讲解更加细致,全文所使用的开发平台均为华清远见FS-MP1A开发板(STM32MP157开发板)针对对FS-MP1A开发板ÿ…...

最适合游戏开发的语言是什么?
建议初学者学习主流的开发技术 主流开发技术有大量成熟的教程、很多可以交流的学习者、及时的学习反馈等;技术的内里基本都是相同的,学习主流技术的经验、知识可以更好更快地疏通学习新知识和技术。 因此,对C#或者C二选一进行学习较好。 Un…...

C语言刷题(7)(字符串旋转问题)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容依旧是复习之前的知识点,那么,就是做一道小小的题目啦,下面,让我们进入C语言的世界吧 实现一个函数,可以左旋字符串中的k个字符。 例如: A…...
有趣且重要的JS知识合集(18)浏览器实现前端录音功能
1、主题描述 兼容多个浏览器下的前端录音功能,实现六大录音功能: 1、开始录音 2、暂停录音 3、继续录音 4、结束录音 5、播放录音 6、上传录音 2、示例功能 初始状态: 开始录音: 结束录音: 录音流程 …...
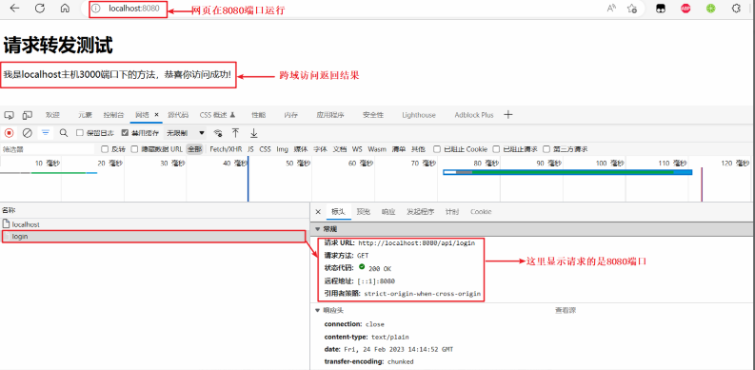
面试官:聊聊你知道的跨域解决方案
跨域是开发中经常会遇到的一个场景,也是面试中经常会讨论的一个问题。掌握常见的跨域解决方案及其背后的原理,不仅可以提高我们的开发效率,还能在面试中表现的更加游刃有余。 因此今天就来和大家从前端的角度来聊聊解决跨域常见的几种方式。…...
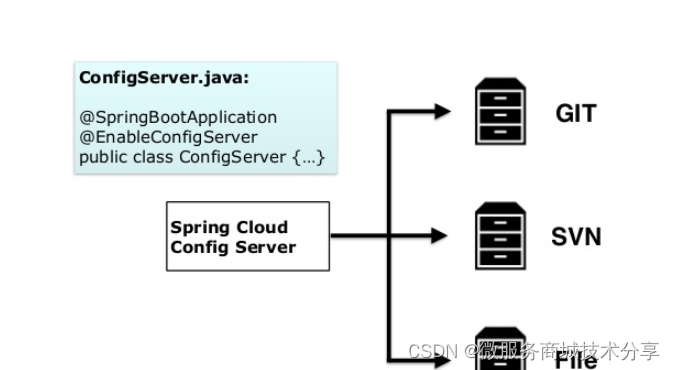
SpringCloud五大核心组件
Consul 等,提供了搭建分布式系统及微服务常用的工具,如配置管理、服务发现、断路器、智能路由、微代理、控制总线、一次性token、全局锁、选主、分布式会话和集群状态等,满足了构建微服务所需的所有解决方案。 服务发现——Netflix Eureka …...
)
Verilog HDL语言入门(二)
强烈建议用同步设计2.在设计时总是记住时序问题3.在一个设计开始就要考虑到地电平或高电平复位、同步或异步复位、上升沿或下降沿触发等问题,在所有模块中都要遵守它4.在不同的情况下用if和case,最好少用if的多层嵌套(1层或2层比较合适&#…...
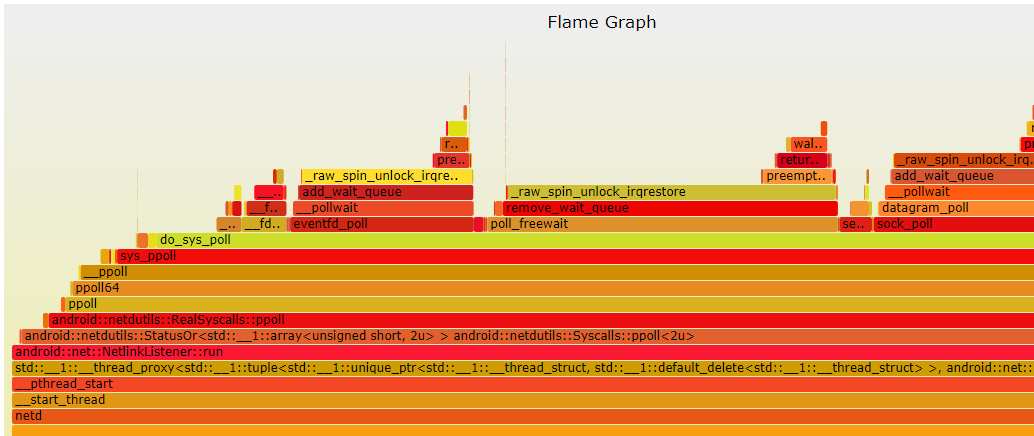
Simpleperf详细使用
一、Simpleperf介绍 Simpleperf是一个强大的命令行工具,它包含在NDK中,可以帮助我们分析应用的CPU性能。Simpleperf可以帮助我们找到应用的热点,而热点往往与性能问题相关,这样我们就可以分析修复热点源。 如果您更喜欢使用命令…...

【算法基础】二分图(染色法 匈牙利算法)
一、二分图 1. 染色法 一个图是二分图,当且仅当,图中不含奇数环。在判别一个图是否为二分图⑩,其实相当于染色问题,每条边的两个点必须是不同的颜色,一共有两种颜色,如果染色过程中出现矛盾,则说明不是二分图。 for i = 1 to n:if i 未染色DFS(i, 1); //将i号点染色未…...

Caputo 分数阶微分方程-慢扩散方程初边值问题基于L1 逼近的空间二阶方法及其Matlab程序实现
2.3.3 Caputo 分数阶一维问题基于 L1 逼近的空间二阶方法 考虑如下时间分数阶慢扩散方程初边值问题 { 0 C D t α u ( x , t ) = u...
 GPIO驱动)
I.MX6ULL_Linux_驱动篇(29) GPIO驱动
Linux 下的任何外设驱动,最终都是要配置相应的硬件寄存器。所以本篇的 LED 灯驱动最终也是对 I.MX6ULL 的 IO 口进行配置,与裸机实验不同的是,在 Linux 下编写驱动要符合 Linux 的驱动框架。I.MX6U-ALPHA 开发板上的 LED 连接到 I.MX6ULL 的 …...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
