【总结】多个条件排序(pii/struct/bool)
目录
pii
struct
bool
pii
现在小龙同学要吃掉它们,已知他有n颗苹果,并且打算每天吃一个。
但是古人云,早上金苹果,晚上毒苹果。由此可见,早上吃苹果和晚上吃苹果的效果是不一样的。
已知小龙同学在第 i 天早上吃苹果能获得的愉悦值为 ai ,晚上吃苹果能获得的愉悦值为 bi 。
但是为了饮食均衡,小龙同学决定必须能选择恰好k天晚上吃苹果。
剩下的 n−k天早上吃苹果,他想知道他能够获得最大的愉悦值是多少。
输入描述:
第一行两个正整数 n,k 表示小龙同学有 nnn 个苹果,n 天吃完,他要选择其中 k 天在晚上吃苹果。
接下来 n 行,每行两个整数 ai,bi 表示小龙同学在第 iii 天早上吃苹果能获得的愉悦值为 ai ,晚上吃苹果能获得的愉悦值为 bi 。
输出描述:
输出一行一个整数表示答案。
示例1
输入
复制
4 3
3 1
4 5
2 3
1 5
输出
复制
16
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;typedef long long LL;
typedef pair<int,int> pii;const int N = 200010;pii a[N];
int n,k;bool cmp(pii a,pii b){return (a.second-a.first)>(b.second-b.first);
}int main(){cin>>n>>k;for(int i=0;i<n;i++){int x=0,y=0;cin>>x>>y;a[i]={x,y};}sort(a,a+n,cmp);int sum=0;for(int i=0;i<k;i++){sum+=a[i].second;}for(int i=k;i<n;i++){sum+=a[i].first;}cout<<sum;return 0; }
struct
小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当 两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。
例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位 之和 13 。
又如, 6 排在 2022 前面, 因为它们的数位之和相同, 而 6 小于 2022 。
给定正整数 �,�n,m, 请问对 1 到 �n 采用这种方法排序时, 排在第 �m 个的元 素是多少?
输入格式
输入第一行包含一个正整数 �n 。
第二行包含一个正整数 �m 。
输出格式
输出一行包含一个整数, 表示答案。
样例输入
13
5样例输出
3#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;typedef long long LL;const int N = 2000010;int n,x;struct st{int m;int sum;
}a[N];int ssum(int n){int s=0;while(n>0){s+=n%10;n/=10;}return s;
}bool cmp(st a,st b){if(a.sum==b.sum) return a.m<b.m;return a.sum<b.sum;
}int main(){cin>>n>>x;for(int i=1;i<=n;i++){a[i].m=i;int t=a[i].m;a[i].sum=ssum(t);} sort(a+1,a+n+1,cmp);cout<<a[x].m;return 0; }bool
#include<iostream>
#include<algorithm>
#include<cstring>using namespace std;typedef long long LL;const int N = 2000010;int n;
int m;
int a[N];int sum(int a){int s=0;while(a>0){s+=a%10;a/=10;}return s;}bool cmp(int a,int b){if(sum(a)<sum(b)) return true;else if(sum(a)>sum(b)) return false;else if(sum(a)==sum(b)) {if(a<b) return true;else return false;}
}int main(){cin>>n>>m;int idx=0;for(int i=0;i<n;i++){a[idx++]=i+1;}sort(a,a+n,cmp);cout<<a[m-1];return 0; }相关文章:
)
【总结】多个条件排序(pii/struct/bool)
目录 pii struct bool pii 现在小龙同学要吃掉它们,已知他有n颗苹果,并且打算每天吃一个。 但是古人云,早上金苹果,晚上毒苹果。由此可见,早上吃苹果和晚上吃苹果的效果是不一样的。 已知小龙同学在第 i 天早上吃苹果能…...
基于stm32mp157 linux开发板ARM裸机开发教程Cortex-A7 开发环境搭建(连载中)
前言:目前针对ARM Cortex-A7裸机开发文档及视频进行了二次升级持续更新中,使其内容更加丰富,讲解更加细致,全文所使用的开发平台均为华清远见FS-MP1A开发板(STM32MP157开发板)针对对FS-MP1A开发板ÿ…...

最适合游戏开发的语言是什么?
建议初学者学习主流的开发技术 主流开发技术有大量成熟的教程、很多可以交流的学习者、及时的学习反馈等;技术的内里基本都是相同的,学习主流技术的经验、知识可以更好更快地疏通学习新知识和技术。 因此,对C#或者C二选一进行学习较好。 Un…...

C语言刷题(7)(字符串旋转问题)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容依旧是复习之前的知识点,那么,就是做一道小小的题目啦,下面,让我们进入C语言的世界吧 实现一个函数,可以左旋字符串中的k个字符。 例如: A…...
有趣且重要的JS知识合集(18)浏览器实现前端录音功能
1、主题描述 兼容多个浏览器下的前端录音功能,实现六大录音功能: 1、开始录音 2、暂停录音 3、继续录音 4、结束录音 5、播放录音 6、上传录音 2、示例功能 初始状态: 开始录音: 结束录音: 录音流程 …...
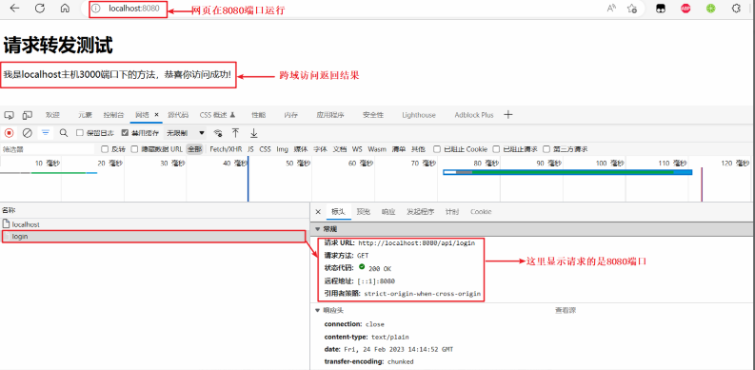
面试官:聊聊你知道的跨域解决方案
跨域是开发中经常会遇到的一个场景,也是面试中经常会讨论的一个问题。掌握常见的跨域解决方案及其背后的原理,不仅可以提高我们的开发效率,还能在面试中表现的更加游刃有余。 因此今天就来和大家从前端的角度来聊聊解决跨域常见的几种方式。…...
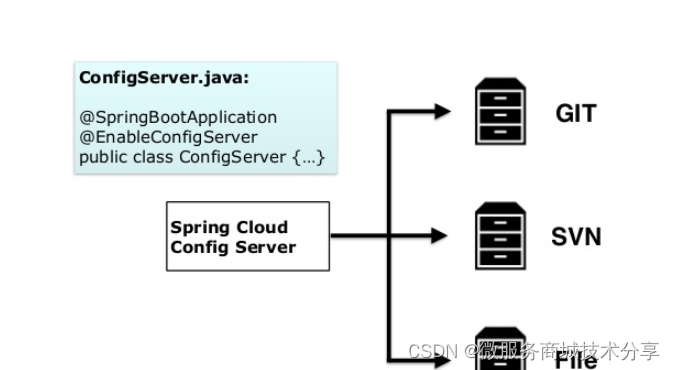
SpringCloud五大核心组件
Consul 等,提供了搭建分布式系统及微服务常用的工具,如配置管理、服务发现、断路器、智能路由、微代理、控制总线、一次性token、全局锁、选主、分布式会话和集群状态等,满足了构建微服务所需的所有解决方案。 服务发现——Netflix Eureka …...
)
Verilog HDL语言入门(二)
强烈建议用同步设计2.在设计时总是记住时序问题3.在一个设计开始就要考虑到地电平或高电平复位、同步或异步复位、上升沿或下降沿触发等问题,在所有模块中都要遵守它4.在不同的情况下用if和case,最好少用if的多层嵌套(1层或2层比较合适&#…...
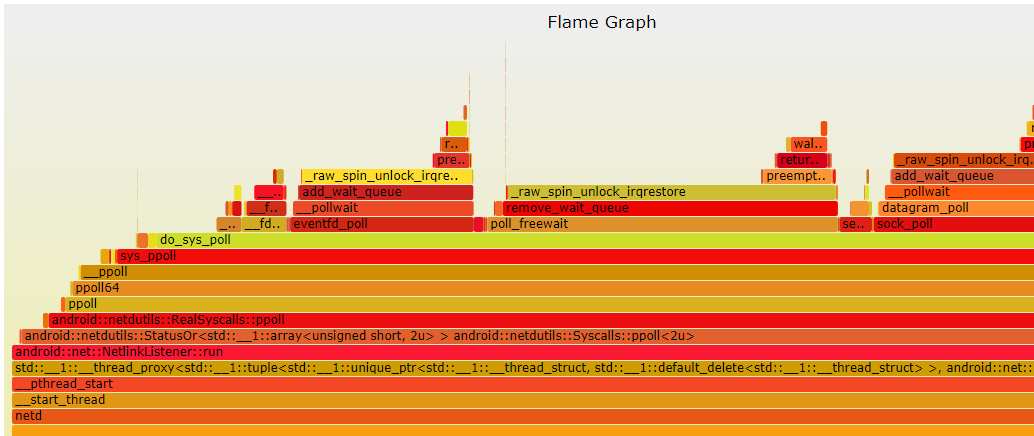
Simpleperf详细使用
一、Simpleperf介绍 Simpleperf是一个强大的命令行工具,它包含在NDK中,可以帮助我们分析应用的CPU性能。Simpleperf可以帮助我们找到应用的热点,而热点往往与性能问题相关,这样我们就可以分析修复热点源。 如果您更喜欢使用命令…...

【算法基础】二分图(染色法 匈牙利算法)
一、二分图 1. 染色法 一个图是二分图,当且仅当,图中不含奇数环。在判别一个图是否为二分图⑩,其实相当于染色问题,每条边的两个点必须是不同的颜色,一共有两种颜色,如果染色过程中出现矛盾,则说明不是二分图。 for i = 1 to n:if i 未染色DFS(i, 1); //将i号点染色未…...

Caputo 分数阶微分方程-慢扩散方程初边值问题基于L1 逼近的空间二阶方法及其Matlab程序实现
2.3.3 Caputo 分数阶一维问题基于 L1 逼近的空间二阶方法 考虑如下时间分数阶慢扩散方程初边值问题 { 0 C D t α u ( x , t ) = u...
 GPIO驱动)
I.MX6ULL_Linux_驱动篇(29) GPIO驱动
Linux 下的任何外设驱动,最终都是要配置相应的硬件寄存器。所以本篇的 LED 灯驱动最终也是对 I.MX6ULL 的 IO 口进行配置,与裸机实验不同的是,在 Linux 下编写驱动要符合 Linux 的驱动框架。I.MX6U-ALPHA 开发板上的 LED 连接到 I.MX6ULL 的 …...

jupyter的安装和使用
目录 ❤ Jupyter Notebook是什么? notebook jupyter 简介 notebook jupyter 组成 网页应用 文档 主要特点 ❤ jupyter notebook的安装 notebook jupyter 安装有两种途径 1.通过Anaconda进行安装 2.通过pip进行安装 启动jupyter notebook ❤ jupyter …...

Springboot新手开发 Cloud篇
前言: 👏作者简介:我是笑霸final,一名热爱技术的在校学生。 📝个人主页:个人主页1 || 笑霸final的主页2 📕系列专栏:后端专栏 📧如果文章知识点有错误的地方,…...

Linux:函数指针做函数参数
#include <stdio.h> #include <stdlib.h> //创建带有函数指针做参数的函数框架api //调用者要先实现回调函数 //调用者再去调用函数框架 //所谓的回调是指 调用者去调用一个带有函数指针做参数的函数框架,函数框架反过来要调用调用者提供的回调函数 …...
Vue3(递归组件) + 原生Table 实现树结构复杂表格
一、递归组件 什么是递归,Javascript中经常能接触到递归函数。也就是函数自己调用自己。那对于组件来说也是一样的逻辑。平时工作中见得最多应该就是菜单组件,大部分系统里面的都是递归组件。文章中我做了按需引入的配置,所以看不到我引用组…...
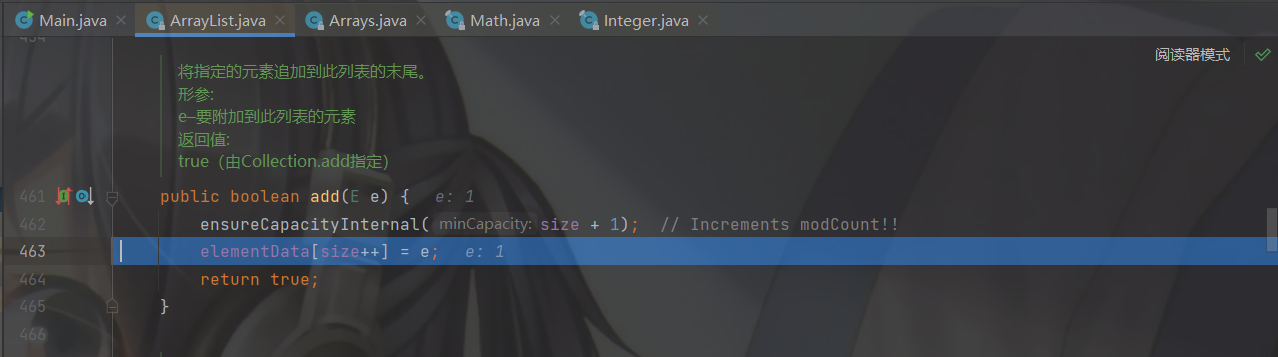
ArrayList底层源码解析
Java源码系列:下方连接 http://t.csdn.cn/Nwzed 文章目录前言一、**ArrayList底层结构和源码分析**无参构造调用创建ArrayList集合无参构造总结:发文3个工作日后 up 会把总结放入前言部分,但也诚邀读者总结,可放入评论区有参构造…...
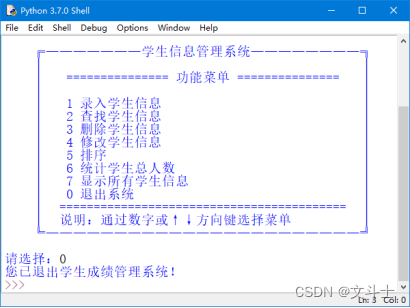
python:DIY字符画的程序使用说明.doc
目录开发环境要求运行方法具体的操作步骤如下:代码示例源码及运行程序下载地址开发环境要求 本系统的软件开发及运行环境具体如下。 操作系统:Windows 7、Windows 10。 Python版本:Python 3.7.0。 开发工具:Python IDLE。 …...

【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解
【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解 文章目录【Python/Opencv】图像权重加法函数:cv2.addWeighted()详解1. 介绍2. API3. 代码示例与效果3.1 代码3.2 效果4. 参考1. 介绍 在OpenCV图像加法cv2.add函数详解详细介绍了图像的加法运…...

容器的老祖宗LXC和Docker的关系
一、什么是LXC? LXC(Linux Container的缩写)是一个基于Linux内核的容器虚拟化技术,它提供了一种轻量级、快速、简便的方式来创建和管理系统容器。与传统虚拟化技术不同,LXC并不会模拟硬件,而是利用Linux内…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
