数据结构:二叉搜索树(简单C++代码实现)
目录
前言
1. 二叉搜索树的概念
2. 二叉搜索树的实现
2.1 二叉树的结构
2.2 二叉树查找
2.3 二叉树的插入和中序遍历
2.4 二叉树的删除
3. 二叉搜索树的应用
3.1 KV模型实现
3.2 应用
4. 二叉搜索树分析
总结
前言
本文将深入探讨二叉搜索树这一重要的数据结构。二叉搜索树不仅是一个功能强大的数据结构,而且在实际应用中展现出了极高的实用性。它以其独特的组织方式,使得查找、插入和删除操作都能在平均对数到线性时间内完成,从而大大提高了数据处理的效率。为了更好地理解二叉搜索树的工作原理,我们使用C++语言实现了一个简单的二叉搜索树。
1. 二叉搜索树的概念
二叉搜索树(Binary Search Tree),也称二叉排序树,是一种特殊的二叉树。二叉搜索树可以为空树。如果不为空树,有以下的性质:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 左子树和右子树也都是二叉搜索树。

2. 二叉搜索树的实现
2.1 二叉树的结构
先自定义一个二叉树结点的类,该类将使用模版。一般来说,有两种类型的二叉搜索树。
- K模型:K模型即只有key作为关键码,自定义结点类型中只需要存储Key即可。
- KV模型:每一个关键码key,都有与之对应的值Value,即<Key,Value>键值对。
下面的代码是两种模型自定义类的实现,把下面的代码放到BSTree.h文件下。分别封装到key和keyValue的命名空间中。我们先实现K模型的二叉树成员函数。再如法炮制实现第二种模型的成员函数。
-
#pragma once #include <iostream> using namespace std;namespace key {template<class K>struct BSTNode{BSTNode(const K& key = K()):_key(key), _left(nullptr), _right(nullptr){}K _key;BSTNode<K>* _left;BSTNode<K>* _right;};template<class K>class BSTree{typedef BSTNode<K> Node;//...private:Node* root;} }namespace keyValue {template<class K, class V>struct BSTNode{BSTNode(const K& key = K(), const V& value = V()):_key(key),_value(value), _left(nullptr), _right(nullptr){}K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;};template<class K, class V>class BSTree{typedef BSTNode<K, V> Node;//...private:Node* root;} }
2.2 二叉树查找
二叉搜索树的查找操作比较简单。
- 函数的返回值是个布尔值。查找成功返回true,失败返回false。
- 从根开始比较关键码,进行查找。如果关键码比根的大往右边查找,比根的小就往左边查找。
- 最多会查找这颗二叉树的高度次,如果走到空,说明这个值不存在。
bool Find(const K& key)
{Node* cur = _root;//如果为空,说明这个值不存在while (cur){//比较关键值大小if (cur->_key < key){cur = cur->right;}else if (cur->_key > key){cur = cur->left;}else{return true;}}return false;
}2.3 二叉树的插入和中序遍历

int arr[] = {11, 7, 18, 9, 14, 4, 23, 8, 16, 10};二叉树的插入操作其实步骤根查找类似,插入具体过程如下:
- 函数的返回值也是布尔值。插入成功返回true,插入失败返回false。
- 如果树为空,直接使用new创建新结点,赋值给root指针。
- 如果树不为空,使用while循环查找新结点的位置,如果找到某个节点存储的值,与插入的值相同,就不需要插入,返回false。此外,还要新定义一个二叉树结点类值,此值用来存储当前结点的父亲结点。因为需要判断新增结点是他的父亲结点左节点还是右节点。
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;
}二叉搜索树可以通过中序遍历得到有序的数据。在类中,定义一个中序遍历的子函数,再传入这棵树的根,进行遍历打印即可。
class BSTree
{//...
public://...void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;
};我们写一个测试函数,测试一下插入函数。
#include "BSTree.h"void Test1()
{int arr[] = { 11, 7, 18, 9, 14, 4, 23, 8, 16, 10 };key::BSTree<int> tree;for (auto& e : arr){tree.Insert(e);}tree.InOrder();tree.Insert(2);tree.Insert(13);tree.InOrder();
}运行结果如下:

2.4 二叉树的删除
二叉树的删除操作就有些麻烦。需要分几种情况:
- 待删除结点没有孩子结点。
- 待删除结点有一个孩子结点。
- 待删除结点有左右孩子结点。
待删除结点没有孩子结点,可以直接释放该节点,使其父亲结点指向空即可。

待删除结点只有一个孩子结点。如下图,14结点有一个右孩子,左孩子为空。先释放14结点,再将其父亲结点的左指针指向16结点即可。如果待删除结点有一个左孩子,操作也是类似。
不过这个有极端情况,如下面的第二张图,如果要删除的是根节点,并且根节点只有左孩子或者右孩子。此时,因为根结点没有父亲结点,所以直接释放根结点,让root指针指向他的孩子结点。


待删除结点有两个孩子结点的情况,就比较麻烦。如下图,思路是找到可以替换的结点,待删除结点的key值替换成该节点的key值,然后再释放这个替换结点,处理结点之间的连接关系。
- 第一步需要查找待删除结点,如果没有找到,返回false。找到待删除结点,进行删除操作。
- 待删除结点的左子树中的最右结点,是左子树中最大的结点,待删除结点的右子树中的最左结点是右子树中最小的结点。我们使用右子树中最左结点来替换待删除结点。
- 我们先定义一个rightMin结点指针变量,用来找右子树中最小的结点,定义一个rightMinP来记录rightMin指向结点的父亲结点。
- 其中rightMin一开始指向待删除结点的右孩子。rightMinP需要指向待删除节点,看第二张图片,如果右子树的最小结点就是待删除结点的右孩子,rightMInP不指向待删除节点,而是指向空,那么我们使用rightMinP这个空指针进行操作会有问题。


bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){ //查找待删除结点if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//删除操作{ // 0-1孩子if (cur->_left == nullptr){if (parent == nullptr)//删除根节点的情况{_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr)//删除根节点的情况{_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{//两个孩子的情况// 右子树的最小节点作为替代节点Node* rightMinP = cur;//不可为空,特殊情况会访问空指针Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;//需要判断右子树最小节点是父亲结点的左孩子还是右孩子if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;
}我们写一个测试函数,测试一些删除函数的功能:
void Test2()
{int arr[] = { 11, 7, 18, 9, 14, 4, 23, 8, 16, 10 };key::BSTree<int> tree;for (auto& e : arr){tree.Insert(e);}tree.InOrder();for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("第%-2d次:", i + 1);tree.Erase(arr[i]);tree.InOrder();}
}运行结果如下:

3. 二叉搜索树的应用
3.1 KV模型实现
上文有提到二叉搜索树有两种模型,其中在现实生活中比较常用的是KV模型。每个关键码key,都有对应的的值Value,即<Key,Value>键值对。
下面是KV模型的代码实现:
namespace keyValue
{template<class K, class V>struct BSTNode{BSTNode(const K& key = K(), const V& value = V()):_key(key),_value(value), _left(nullptr), _right(nullptr){}K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;};template<class K, class V>class BSTree{typedef BSTNode<K, V> Node;public:BSTree() = default;BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 0-1孩子if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{// 两个孩子的情况// 右子树的最小节点作为替代节点Node* rightMinP = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;cur->_value = rightMin->_value;if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << " ";_InOrder(root->_right);}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);}private:Node* _root = nullptr;};
};3.2 应用
二叉搜索树KV模型的应用有许多
- 最经典的就是双语词典,英汉词典中,每个英文都有对应的中文,构成<word, chinese>键值对。
- 中国公民每个人都有对象的身份证号码,即<中国人,身份证号码>键值对。
- 还可以用来统计词语出现的次数,词语和其出现的次数就构成<word,count>键值对。
void TestBsTree3()
{keyValue::BSTree<string, string> dict;dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("apple", "苹果");dict.Insert("sort", "排序");dict.Insert("love", "爱");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << "->" << ret->_value << endl;}else{cout << "重新输入" << endl;}}
}运行结果如下:

这是统计词语出现次数
void TestBSTree4()
{// 统计物品出现的次数string arr[] = { "书本", "笔", "书本", "笔", "书本", "书本", "笔", "书本", "橡皮", "书本", "橡皮" };keyValue::BSTree<string, int> countTree;for (const auto& str : arr){// 先查找物品在不在搜索树中// 1、不在,说明物品第一次出现,则插入<物品, 1>// 2、在,则查找到的节点中水果对应的次数++auto ret = countTree.Find(str);if (ret == NULL)countTree.Insert(str, 1);elseret->_value++;}countTree.InOrder();
}运行结果如下:

4. 二叉搜索树分析
二叉搜索树的插入和删除操作,都需要先进行查找。查找操作一般最多查找这颗树的高度次,如果二叉搜索树是一个满二叉树或者完全二叉树,效率很高。可当二叉树退化成下图中右边这颗二叉树,基本上像链表的形态,那么查找的速度比原来慢了很多。
- 最好的情况,二叉搜索树是接近一颗满二叉树,查找的时间复杂度是O(logN)。
- 最坏的情况,二叉搜索树退化成只有单链,像链表的形态,查找的时间复杂度是O(N)。
因此,在二叉搜索树的基础上,又出现了平衡二叉搜索树,如AVL树和红黑树,会调整二叉树成为接近满二叉树的形态。

总结
通过本文的阐述,相信你应该对二叉搜索树的基本概念、特性以及操作方法已经有了一定的了解。不过想要掌握这个数据结构,还需要亲自上手编写一个二叉搜索树的代码。通过编码实践,才能更深刻体会到内部的工作机制。
创作不易,希望这篇文章能给你带来启发和帮助,如果喜欢这篇文章,请留下你的三连,你的支持的我最大的动力!!!

相关文章:

数据结构:二叉搜索树(简单C++代码实现)
目录 前言 1. 二叉搜索树的概念 2. 二叉搜索树的实现 2.1 二叉树的结构 2.2 二叉树查找 2.3 二叉树的插入和中序遍历 2.4 二叉树的删除 3. 二叉搜索树的应用 3.1 KV模型实现 3.2 应用 4. 二叉搜索树分析 总结 前言 本文将深入探讨二叉搜索树这一重要的数据结构。二…...

深入理解Prompt工程
前言:因为大模型的流行,衍生出了一个小领域“Prompt工程”,不知道大家会不会跟小编一样,不就是写提示吗,这有什么难的,不过大家还是不要小瞧了Prompt工程,现在很多大模型把会“Prompt工程”作为…...
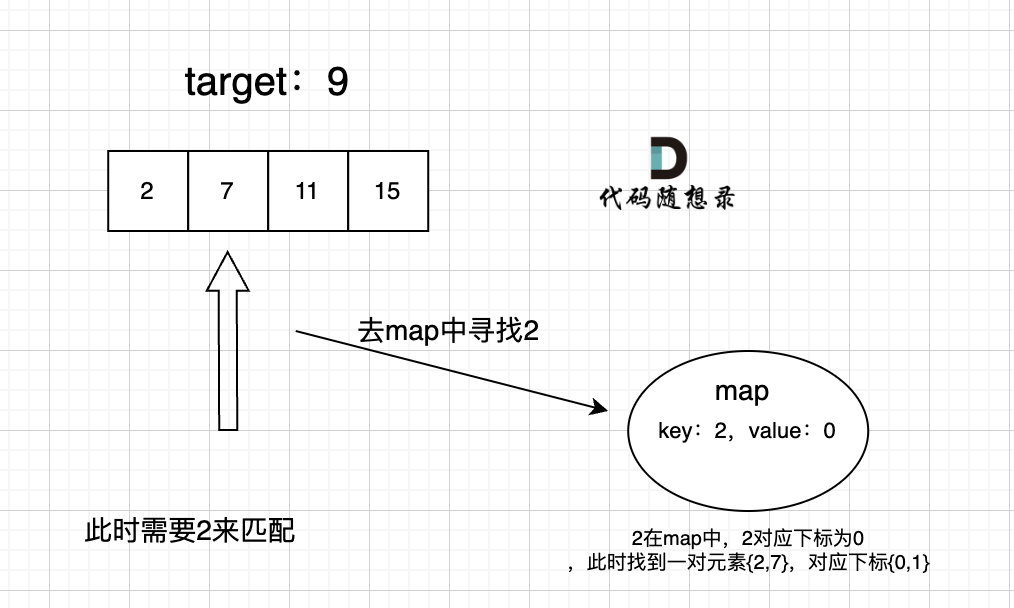
代码随想录算法训练营day6 | 242.有效的字母异位词、349. 两个数组的交集、202. 快乐数、1.两数之和
文章目录 哈希表键值 哈希函数哈希冲突拉链法线性探测法 常见的三种哈希结构集合映射C实现std::unordered_setstd::map 小结242.有效的字母异位词思路复习 349. 两个数组的交集使用数组实现哈希表的情况思路使用set实现哈希表的情况 202. 快乐数思路 1.两数之和思路 总结 今天是…...

vue3 vxe-table 点击行,不显示选中状态,加上设置isCurrent: true就可以设置选中行的状态。
1、上个图,要实现这样的: Vxe Table v4.6 官方文档 2、使用 row-config.isCurrent 显示高亮行,当前行是唯一的;用户操作点击选项时会触发事件 current-change <template><div><p><vxe-button click"sel…...

Linux没有telnet 如何测试对端的端口状态
前段时间有人问uos没有telnet,又找不到包。 追问了一下为什么非要安装telnet,答复是要测试对端的端口号。 这里简单介绍一下,测试端口号的方法有很多,telent只是在windows上经常使用,linux已很少安装并使用该命令&…...

花几千上万学习Java,真没必要!(二十九)
1、基本数据类型包装类: 测试代码1: package apitest.com; //使用Integer类的不同方法处理整数。 //将字符串转换为整数(parseInt)和Integer对象(valueOf), //将整数转换回字符串(…...

C#如何引用dll动态链接库文件的注释
1、dll动态库文件项目生成属性中要勾选“XML文档文件” 注意:XML文件的名字切勿修改。 2、添加引用时XML文件要与DLL文件在同一个目录下。 3、如果要是添加引用的时候XML不在相同目录下,之后又将XML文件复制到相同的目录下,需要删除引用&am…...

WordPress原创插件:自定义文章标题颜色
插件设置截图 文章编辑时,右边会出现一个标题颜色设置,可以设置为任何颜色 更新记录:从输入颜色css代码,改为颜色选择器,更方便! 插件免费下载 https://download.csdn.net/download/huayula/89585192…...

Unity分享:继承自MonoBehaviour的脚步不要对引用类型的字段在声明时就初始化
如果某些字段在每个构造函数中都要进行初始化,很多人都喜欢在字段声明时就进行初始化,对于一个非继承自MonoBehaviour的脚步,这样做是没有问题的,然而继承自MonoBehaviour后就会造成内存的浪费,为什么呢?因…...

.NET Core中如何集成RabbitMQ
在.NET Core中集成RabbitMQ主要涉及到几个步骤,包括安装RabbitMQ的NuGet包、建立连接、定义队列、发送和接收消息等。下面是一个简单的指南来展示如何在.NET Core应用程序中集成RabbitMQ。 目录 1. 安装RabbitMQ.Client NuGet包 2. 建立连接 3. 定义队列 4. 发…...

嵌入式C++、STM32、MySQL、GPS、InfluxDB和MQTT协议数据可视化:智能物流管理系统设计思路流程(附代码示例)
目录 项目概述 系统设计 硬件设计 软件设计 系统架构图 代码实现 1. STM32微控制器与传感器代码 代码讲解 2. MQTT Broker设置 3. 数据接收与处理 代码讲解 4. 数据存储与分析 5. 数据分析与可视化 代码讲解 6. 数据可视化 项目总结 项目概述 随着电子商务的快…...

.net core docker部署教程和细节问题
在.NET Core中实现Docker一键部署,通常涉及以下几个步骤:编写Dockerfile以定义镜像构建过程、构建Docker镜像、运行Docker容器,以及(可选地)使用自动化工具如Docker Compose或CI/CD工具进行一键部署。以下是一个详细的…...

php数据库链接
Php超全局变量 GET 和 POST 都创建一个数组(例如 array( key1 > value1, key2 > value2, key3 > value3, ...))。此数组包含键/值对,其中 键是表单控件的名称,…...

python+vue3+onlyoffice在线文档系统实战20240726笔记,左侧菜单实现和最近文档基本实现
解决右侧高度过高的问题 解决方案:去掉右侧顶部和底部。 实现左侧菜单 最近文档,纯粹文档 我的文档,既包括文件夹也包括文件 共享文档,别人分享给我的 基本实现代码: 渲染效果: 简单优化 设置默认菜…...

vue中的nexttrick
Vue.js 是一个用于构建用户界面的渐进式框架,它允许开发者通过声明式的数据绑定来构建网页应用。在 Vue 中,nextTick 是一个非常重要的 API,它用于延迟回调的执行,直到下次 DOM 更新循环之后。 为什么使用 nextTick? …...

【BUG】已解决:ModuleNotFoundError: No module named ‘requests‘
ModuleNotFoundError: No module named ‘requests‘ 目录 ModuleNotFoundError: No module named ‘requests‘ 【常见模块错误】 【解决方案】 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班出身&a…...

深入理解JS中的发布订阅模式和观察者模式
发布/订阅模式(Publish/Subscribe)和观察者模式(Observer Pattern)在概念上非常相似,都是用于实现对象之间的松耦合通信。尽管它们在实现细节和使用场景上有所不同,但核心思想是相通的。 观察者模式 直接通信:在观察者模式中,观察者(Observer)直接订阅主题(Subject…...

网站IPv6支持率怎么检测?
在当今数字化的时代,IPv6的推广和应用已经成为网络发展的重要趋势。IPv6拥有更大的地址空间、更高的安全性和更好的性能,对于满足日益增长的网络需求至关重要。对于网站所有者和管理员来说,了解其网站对IPv6的支持率是评估网站性能和兼容性的…...

react中简单的配置路由
1.安装react-router-dom npm install react-router-dom 2.新建文件 src下新建page文件夹,该文件夹下新建login和index文件夹用于存放登录页面和首页,再在对应文件夹下分别新建入口文件index.js; src下新建router文件用于存放路由配置文件…...

RocketMQ消息短暂而又精彩的一生(荣耀典藏版)
目录 前言 一、核心概念 二、消息诞生与发送 2.1.路由表 2.2.队列的选择 2.3.其它特殊情况处理 2.3.1.发送异常处理 2.3.2.消息过大的处理 三、消息存储 3.1.如何保证高性能读写 3.1.1.传统IO读写方式 3.2零拷贝 3.2.1.mmap() 3.2.2sendfile() 3.2.3.CommitLog …...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
