Wonder3D 论文学习
论文链接:https://arxiv.org/abs/2310.15008
代码链接:https://github.com/xxlong0/Wonder3D
解决了什么问题?
随着扩散模型的提出,3D 生成领域取得了长足进步。从单张图片重建出 3D 几何是计算机图形学和 3D 视觉的基础任务,在 VR、游戏、3D 内容生成、机器人领域有广泛的应用。由于该任务是不适定的,需要推理出可见和不可见区域的 3D 几何结构。该种能力的构建需要大量的 3D 世界的知识。
部分工作(如 DreamField, DreamFusion, Magic3D)需要通过 score distillation sampling 来蒸馏出 2D 图像扩散模型或视觉语言模型的知识,从文本或图像创建出 3D 模型。尽管效果不错,这些方法都面临着两个问题:效率和一致性。每个形状的优化通常需要几万次的迭代,这涉及到全图渲染和扩散模型的推理。因此,优化一个形状甚至会耗费数小时。此外,2D 先验模型在每次迭代时只考虑一个视角,使得每个视角都接近于输入图像,这会造成生成的 3D 形状不一致。
另一部分的工作则尝试通过网络推理来生成 3D 的几何结构如点云、meshes、神经场,避免耗时的优化。此类方法大多在 3D assets 上训练 3D 生成扩散模型。但是,由于现有的 3D 数据集规模有限,这些方法都缺乏足够的泛化性,只能生成特定类别的形状。
另一些方法如 SyncDreamer 和 MVDream 直接生成多视角 2D 图像。这些工作增强了图像生成的多视角一致性,能从生成的多视角 2D 图像中恢复出 3D 形状。本文方法也采用了多视角生成的机制,因为 2D 表征效率高、灵活性强。但是只依赖于彩色图像,生成形状的保真度就差一些,它们要么很难恢复几何细节,要么计算量惊人。
基于 score distillation sampling 的方法能够从 2D 的扩散先验信息中恢复出 3D 结构,但通常都非常耗时,生成的几何形状不一致。另一些工作则通过快速的网络推理来产生 3D 信息,但质量都比较差,缺乏几何细节信息。
提出了什么方法?

为了解决保真度、一致性、泛化性和效率的问题,本文提出了一个单视角 3D 重建方法,用一个跨域扩散模型来生成多视角、一致性的法线图和对应的彩色图像。核心思想是扩展 stable diffusion,对两个不同域(法线和色彩)的协同分布来建模。作者证明,可以通过一个 domain switcher 和跨域注意力机制来实现。Domain switcher 允许扩散模型生成法线图或彩色图,而跨域注意力机制则在这两个域之间传递信息,提升效率和质量。最后为了从生成视角中提取表面结构,作者提出了一个更加鲁棒的几何法线融合算法,能够重建出干净、高质量(如上图所示)的几何结构。
作者在 Google Scanned Object 数据集和各种不同风格的 2D 图像上做了实验。实验表明 Wonder3D 能够高效地恢复出高质量的几何结构。
1. Diffusion Models
扩散模型通过一个特殊的退化过程,逐步地恢复图像,它采用了一个前向马尔可夫链和反向马尔可夫链。给定一个来自于数据分布 p ( z ) p(z) p(z)的样本 z 0 z_0 z0,去噪扩散模型的前向计算会输出一个序列的加了噪声的数据 { z t ∣ t ∈ ( 0 , T ) } \{z_t | t\in(0,T)\} {zt∣t∈(0,T)},其中 z t = α t z 0 + σ t ϵ z_t = \alpha_t z_0 + \sigma_t \epsilon zt=αtz0+σtϵ, ϵ \epsilon ϵ 是从分布 N ( 0 , 1 ) \mathcal{N}(0,1) N(0,1)中随机选择的噪声, α t , σ t \alpha_t, \sigma_t αt,σt 是 noise schedule 的固定序列。逐步地对目标图像进行前向计算,直到图像变成完全的高斯噪声。然后使用逆马尔可夫链,逐步地去除图像上的噪声,通过预测添加的随机噪声 ϵ \epsilon ϵ,从 z t z_{t} zt 恢复出 z t − 1 z_{t-1} zt−1。
2. The Distribution of 3D assets
以前的工作使用了 3D 表征如点云和神经辐射场,作者认为,3D assets 的分布(记做 p a ( z ) p_{a}(\mathbf{z}) pa(z))可以建模成对应的 2D 多视角法线图和彩色图像之间的协同分布。特别地,给定一组相机 { π 1 , π 2 , . . . , π K } \{\pi_1, \pi_2, ..., \pi_K\} {π1,π2,...,πK} 以及一个条件输入图像 y y y,
p a ( z ) = p n c ( n 1 : K , x 1 : K ∣ y ) p_a(\mathbf{z})=p_{nc}(n^{1:K}, x^{1:K}|y) pa(z)=pnc(n1:K,x1:K∣y)
其中 p n c p_{nc} pnc 是图像 y y y 的法线图 n 1 : K n^{1:K} n1:K 和彩色图 x 1 : K x^{1:K} x1:K 的分布。在后续讨论中,作者省去了记号 y y y。因此,我们的目标是学习一个模型 f f f,合成不同相机姿态的多个法线图和彩色图,记做:
( n 1 : K , x 1 : K ) = f ( y , π 1 : K ) (n^{1:K}, x^{1:K}) = f(y, \pi_{1:K}) (n1:K,x1:K)=f(y,π1:K)
通过 2D 表征,我们的方法用 2D 扩散模型(基于几十亿张图像训练得到)构建,它具有很强的 zero-shot 泛化能力。另一方面,法线图描述了物体表面的起伏波动,编码了丰富的细节几何信息。我们可以从 2D 法线图提取高质量的 3D 几何信息。最后,我们可以将扩散机制的这个跨域协同分布表示成一个马尔可夫链:
p ( n T 1 : K , x T 1 : K ) ∏ t p θ ( n t − 1 1 : K , x t − 1 1 : K ∣ n t 1 : K , x t 1 : K ) p(n_T^{1:K}, x_T^{1:K}) \prod_t{p_{\theta}(n_{t-1}^{1:K}, x_{t-1}^{1:K} | n_{t}^{1:K}, x_{t}^{1:K})} p(nT1:K,xT1:K)t∏pθ(nt−11:K,xt−11:K∣nt1:K,xt1:K)
其中 p ( n T 1 : K , x T 1 : K ) p(n_T^{1:K}, x_T^{1:K}) p(nT1:K,xT1:K) 是高斯噪声。核心问题是描述出分布 p θ p_\theta pθ,这样我们就能从这个马尔可夫链中采样,生成出法线图和彩色图像。
3. 方法
本文提出了一个多视角跨域的扩散机制,在两个不同的域上运行,生成多视角一致的法线图和彩色图。整体架构如下图所示。首先,采用一个多视角扩散模型,生成多视角法线图和彩色图,使用多视角注意力要求不同的视角具有一致性。其次,domain switcher 允许扩散模型在多个域中运行,无需重新训练现有的 Stable Diffusion。因此,我们可以利用基础模型的泛化能力,它们一般是在大规模数据上训练得到。作者提出了一个跨域注意力,在法线域和彩色图像域之间传递信息,确保几何和视觉信息的一致性。最终,该几何法线融合方法能从 2D 法线图和彩色图像中恢复高质量的几何信息和外观信息。

3.1 Consistent Multi-view Generation
2D 扩散模型单独地生成每个图像,生成的图像在多个视角的视觉和几何上并非一致的。为了增强不同视角的一致性,像 SyncDreamer 和 MVDream 一样,作者利用了注意力机制来促进不同视角的信息传递,隐式地编码多视角图像之间的关系,如下图所示。

将原来的自注意力层扩展至全局范围,允许注意力层连接到其它视角的图像。不同视角的 keys 和 values 彼此连接,促进信息的传递。通过在注意力层共享不同视角的信息,扩散模型能够感知到多视角的关系,能够生成一致的多视角彩色图像和法线图。
3.2 Cross-Domain Diffusion
本文模型基于一个预训练的 2D stable diffusion 模型构建。但是,当前的 2D 扩散模型都是针对单个域设计的,那么挑战就是如何有效地将 stable diffusion 扩展至多个域。
Naive Solutions
为了实现此目的,作者探索了多个可能的设计。直接方案就是在 UNet 模块的输出增加四个通道,表示其它的域。因此,扩散模型能同时输出法线图和彩色图像。但是,我们注意到该设计收敛速度慢,泛化性差。这是因为通道扩张可能影响 stable diffusion 的预训练权重,造成灾难性的模型遗忘。
回到第一个等式,可以将协同分布拆分为两个条件分布:
q a ( z ) = q n ( n 1 : K ) ⋅ q c ( x 1 : K ∣ n 1 : K ) q_a(\mathbf{z}) = q_n(n^{1:K})\cdot q_c(x^{1:K} | n^{1:K}) qa(z)=qn(n1:K)⋅qc(x1:K∣n1:K)
我们可以一开始训练一个扩散模型来生成法线图,然后基于生成的法线图,训练另一个扩散模型来生成彩色图像。但是,这个双阶段框架会增加计算成本,也会造成表现退化的问题。
Domain switcher
为了克服这些问题,作者通过 domain switcher 设计了一个跨域的扩散机制,记做 s s s。Switcher s s s 是一个一维的向量,标记不同的域,将该 switcher 输进扩散模型作为额外的输入使用。因此,第二个等式就可以扩展成:
n 1 : K , x 1 : K = f ( y , π 1 : K , s n ) , f ( y , π 1 : K , s c ) n^{1:K}, x^{1:K} = f(y, \pi_{1:K}, s_n), f(y, \pi_{1:K}, s_c) n1:K,x1:K=f(y,π1:K,sn),f(y,π1:K,sc)
Switcher s s s 首先用 positional encoding 做编码,再和 time embedding 拼接到一起。然后注入 stable diffusion 的 UNet。实验表明,这个微小的变动不会改变预训练先验,而收敛速度会更快、鲁棒性和泛化性会更强。
Cross-domain Attention
有了 switcher 后,扩散模型能生成两个不同的域。但是要注意到,对于单个视角而言,彩色图像和法线图并不是几何一致的。为了解决这个问题,需要确保法线图和彩色图的一致性,于是作者加入了一个跨域注意力机制来促进信息在两个域之间传递。该机制的目的是确保生成的图像能在几何和外观上对齐。
该跨域注意力层与原版的自注意力层结构相同,位于 UNet 每个 transformer 模块的 cross-attention 层之前,如上图所示。在跨域注意力层,将法线域和彩色图像域的 keys 和 values 结合起来,经过注意力操作计算。该设计确保了生成的彩色图像和法线图紧密是关联的,增强二者的几何一致性。
3.3 Textured Mesh Extraction
为了从 2D 法线图和彩色图中直接提取 3D 几何结构,作者优化了一个 neural implicit signed distance field(SDF),融合生成的 2D 数据。不像其它的表征(如 meshes),SDF 更加简洁,判别度更强。
SDF 是一个函数,它为空间中的每个点返回一个值,表示该点到最近表面的距离。如果点在表面内部,返回负值;如果点在表面外部,返回正值。SDF函数通常定义为: f ( x ) = 距离 − ϵ f(x)=\text{距离}-\epsilon f(x)=距离−ϵ。其中 ϵ \epsilon ϵ 是一个小的正数,用于确保函数在表面上的值为零。利用神经网络来学习 SDF 函数的参数。这意味着神经网络通过训练,学习如何从输入数据(如图像或点云)中推断出距离场。
但是,无法使用现有的基于 SDF 的重建方法(如 NeuS)。这些方法都是为真实拍摄的图像设计的,需要密集的输入视角。然而,本文方法生成的视角相对稀疏,生成的法线图和彩色图像可能会有一些错误预测的像素。在几何优化时,这些错误可能会累加,造成几何结构的畸变或不完整。于是作者提出了一个几何优化机制。
Optimization Objectives
有了法线图 G 0 : N G_{0:N} G0:N和彩色图 H 0 : N H_{0:N} H0:N后,首先利用分割模型从法线图和彩色图中分割出物体的 masks M 0 : N M_{0:N} M0:N。随机选取一个 batch 的像素点和它们在世界空间 P = { g k , h k , m k , v k } P=\{g_k, h_k, m_k, \mathbf{v}_k\} P={gk,hk,mk,vk}对应的射线,其中 g k g_k gk是第 k k k个采样像素的法线值, h k h_k hk是第 k k k个像素的颜色值, m k ∈ { 0 , 1 } m_k\in \{0,1\} mk∈{0,1}是第 k k k个像素的 mask 值, v k \mathbf{v}_k vk是第 k k k个射线的方向。
整体的优化函数如下,
L = L n o r m a l + L r g b + L m a s k + R e i k + L s p a r s e + L s m o o t h \mathcal{L}=\mathcal{L}_{normal}+\mathcal{L}_{rgb}+\mathcal{L}_{mask}+\mathcal{R}_{eik}+\mathcal{L}_{sparse}+\mathcal{L}_{smooth} L=Lnormal+Lrgb+Lmask+Reik+Lsparse+Lsmooth
其中 L n o r m a l \mathcal{L}_{normal} Lnormal表示法线损失, L r g b \mathcal{L}_{rgb} Lrgb是 MSE 损失,计算渲染颜色 h ^ k \hat{h}_k h^k和生成颜色 h k h_k hk的损失。 L m a s k \mathcal{L}_{mask} Lmask是一个二元交叉熵损失,计算渲染 mask m ^ k \hat{m}_k m^k 和生成 mask m k m_k mk 的损失。 R e i k \mathcal{R}_{eik} Reik 表示 eikonal 正则项,促使 SDF 的梯度的级数为单位长度。 L s p a r s e \mathcal{L}_{sparse} Lsparse 是稀疏正则项。 L s m o o t h \mathcal{L}_{smooth} Lsmooth 是一个 3D 平滑正则项,迫使 SDF 梯度在 3D 空间平滑。
Eikonal 正则项是一种在数学和物理中用于描述波动现象的数学模型中常见的项。它与波动方程中的相位速度有关,尤其是在描述光波或其他类型的波的传播时。Eikonal 方程是一个非线性偏微分方程,通常用于描述波动现象中的相位波前。它的形式可以简化为 ∣ ∇ ϕ ∣ 2 = n 2 |\nabla \phi|^2=n^2 ∣∇ϕ∣2=n2,其中 ϕ \phi ϕ是相位函数, ∇ \nabla ∇是梯度算子, n n n是介质的折射率。在波动方程中,正则项是指那些描述波动传播的项。Eikonal 正则项特别关注波前的形状和传播速度。
Geometry-aware Normal Loss
由于 SDF 表征的本质不同,我们可以通过计算 SDF 的二阶导数获得优化后的 SDF 的法线值 g ^ \hat{g} g^。最大化 SDF g ^ \hat{g} g^ 的法线和生成法线 g g g 的相似度,提供 3D 几何监督信号。为了克服不同视角下法线的细微错误,作者提出了一个几何法线损失:
L n o r m a l = 1 ∑ w k ∑ w k ⋅ e k , e k = ( 1 − cos ( g k ^ , g k ) ) \mathcal{L}_{normal}=\frac{1}{\sum{w_k}}\sum{w_k \cdot e_k}, \quad e_k=(1-\cos{(\hat{g_k}, g_k)}) Lnormal=∑wk1∑wk⋅ek,ek=(1−cos(gk^,gk))
其中 e k e_k ek 是第 k k k个射线的 SDF 的法线 g ^ k \hat{g}_k g^k 和生成法线 g k g_k gk 之间的损失, cos ( ⋅ , ⋅ ) \cos(\cdot, \cdot) cos(⋅,⋅) 表示余弦函数, w k w_k wk 是几何权重:
w k = { 0 , cos ( v k , g k ) > ϵ , exp ( ∣ cos ( v k , g k ) ∣ ) , cos ( v k , g k ) ≤ ϵ w_k=\left\{ \begin{aligned} 0 &, & \cos(\mathbf{v}_k, \mathbf{g}_k)>\epsilon, \\ \exp{(|\cos(\mathbf{v}_k, \mathbf{g}_k)|)} &, & \cos(\mathbf{v}_k, \mathbf{g}_k)\leq \epsilon \end{aligned} \right. wk={0exp(∣cos(vk,gk)∣),,cos(vk,gk)>ϵ,cos(vk,gk)≤ϵ
其中 exp \exp exp表示指数函数, ∣ ⋅ ∣ |\cdot| ∣⋅∣ 表示绝对值函数, ϵ \epsilon ϵ 是接近于 0 0 0的负数阈值,我们计算生成法线 g k g_k gk 和第 k k k个射线的观测方向 v k \mathbf{v}_k vk的角度余弦值。
在计算机视觉中,射线的观察方向可以用于估计场景的深度和结构。例如,通过分析从不同视点发出的射线的交点,可以重建三维场景。
该方法的设计逻辑就是法线的朝向角,设定为面向外的,而观测方向是面向里的。这就确保了法线向量和观测射线的角度不低于 9 0 ∘ 90^\circ 90∘。如果偏离了这个评价标准,说明生成的法线不够准确。
而且,值得注意的是,从多个不同观测点都能看到优化后形状的 3D 点。因此,它会受到对应这些视角的多条法线影响。但是,如果多条法线无法展现完美的一致性,几何监督信号就会变得模楞两可,产生不准确的几何结构。为了解决这个问题,作者引入了一个加权机制,而非同等地看待这些法线。如果一条法线与观测射线有更大的夹角,则权重就更大。这增强了几何监督过程的准确率。
法线是一个向量,它在几何体的表面上的某一点与该表面垂直。在二维空间中,法线是一个垂直于曲线的直线;在三维空间中,法线是一个垂直于表面的平面。法线通常用向量表示。如果一个曲面由函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 定义,则该曲面上点 ( x , y , f ( x , y ) ) (x,y, f(x,y)) (x,y,f(x,y)) 的法线可以通过曲面的梯度向量 ∇ f \nabla{f} ∇f 来确定。
Outlier-dropping Losses
除了法线损失,mask 损失和颜色损失也用于优化几何结构和外观特征。但是,在彩色图像和 masks 中不可避免地会出现一些错误的点,在优化的过程中会逐步累加,产生异常的表面和空洞。于是作者提出了一个简单而有效的策略,叫做 outlier-dropping loss。以颜色损失计算为例,除了简单地将每一步的所有采样射线的颜色求和,作者首先以倒序的顺序将这些损失排序,舍弃损失最大的那部分。这是因为错误预测和其它视角之间缺乏足够的一致性。加入了该策略后,优化后的几何结构就剔除了错误的几何结构和畸变区域。

相关文章:

Wonder3D 论文学习
论文链接:https://arxiv.org/abs/2310.15008 代码链接:https://github.com/xxlong0/Wonder3D 解决了什么问题? 随着扩散模型的提出,3D 生成领域取得了长足进步。从单张图片重建出 3D 几何是计算机图形学和 3D 视觉的基础任务&am…...

【MySQL进阶之路 | 高级篇】显式事务和隐式事务
使用事务有两种方式:显式事务和隐式事务。 1. 显式事务 步骤1: START TRANSACTION或者BEGIN,作用是显式开启一个事务。 START TRANSACTION语句相较于BEGIN特别之处在于,后面能跟几个修饰符。比如: READ ONLY&…...

Ruby、Python、Java 开发者必备:Codigger之软件项目体检
在编程的广阔天地里,Ruby、Python 和 Java 开发者们各自凭借着独特的语言特性,构建着精彩纷呈的应用世界。然而,无论使用哪种语言,确保项目的高质量始终是至关重要的目标。而 Codigger 项目体检则成为了实现这一目标的得力助手&am…...

day05 Router、vuex、axios
配置 router和vuex需要在创建vue项目的时候,开始的时候选择Manually select features,于是就可以在下一个创建配置讯问中选择router和vuex。 axios则需要执行命令行: npm install axios -S 之后再在需要发送请求的view导入即可。 router…...

yolov5-7在opencv里跑自己的onnx模型
先把模型放在如下目录 运行如下代码 import cv2 import numpy as npclass Onnx_clf:def __init__(self, onnx:strdnn_model1/plane02.onnx, img_size640, classlist:list[plane]) -> None: func: 读取onnx模型,并进行目标识别para onnx:模型路径img_size:输出图片大小,和模…...

JVM 11 的优化指南:如何进行JVM调优,JVM调优参数有哪些
这篇文章将详细介绍如何进行JVM 11调优,包括JVM 11调优参数及其应用。此外,我将提供12个实用的代码示例,每个示例都会结合JVM启动参数和Java代码。 本文已收录于,我的技术网站 java-broke.site,有大厂完整面经&#x…...

nginx的配置和使用
一、nginx支持win和linux版本的下载,选择合适的版本进行安装 二、配置文件注解 重点的几个参数进行注释: 1、listen 要监听的服务的端口,符合这个端口的才会被监听 server_name要监听的服务地址,可能是ip,也可能是域名…...

mysql面试(六)
前言 本章节详细讲解了一下mysql执行计划相关的属性释义,以及不同sql所出现的不同效果 执行计划 一条查询语句经过mysql查询优化器的各种基于成本和各种规则优化之后,会生成一个所谓的 执行计划,这个执行计划展示了这条查询语句具体查询方…...

6.乳腺癌良性恶性预测(二分类、逻辑回归、PCA降维、SVD奇异值分解)
乳腺癌良性恶性预测 1. 特征工程1.1 特征筛选1.2 特征降维 PCA1.3 SVD奇异值分解 2. 代码2.1 逻辑回归、二分类问题2.2 特征降维 PCA2.3 SVD奇异值分解 1. 特征工程 专业上:30个人特征来自于临床一线专家,每个特征和都有医学内涵;数据上&…...
)
Vue3响应式高阶用法之markRaw()
Vue3响应式高阶用法之markRaw() 文章目录 Vue3响应式高阶用法之markRaw()一、简介二、使用场景2.1 避免性能开销2.2 防止意外修改 三、基本使用3.1 标记对象 四、功能详解4.1 markRaw与reactive的区别4.2 markRaw与ref的区别 五、最佳实践及案例5.1 使用大型第三方库对象5.2 静…...
免费SSL证书的安全性与获取指南
SSL证书是一种数字凭证,用于加密用户与网站之间的信息交换,以确保传输的数据不被第三方窃取。它像是一个数字版的密封印章,为数据的传输过程提供了一层保护膜。 免费的SSL证书通常由CA机构提供,它们同样可以提供基础数据的加密服…...

【CN】Argo 持续集成和交付(一)
1.简介 Argo 英 [ˈɑ:ɡəu] 美 [ˈɑrˌɡo] Kubernetes 原生工具,用于运行工作流程、管理集群以及正确执行 GitOps。 Argo 于 2020 年 3 月 26 日被 CNCF 接受为孵化成熟度级别,然后于 2022 年 12 月 6 日转移到毕业成熟度级别。 argoproj.github.i…...

Unity3D 自定义Debug双击溯源问题详解
前言 在Unity3D的开发过程中,经常需要处理各种交互和事件,其中双击事件是常见的需求之一。然而,由于Unity自带的双击检测机制并不完善,开发者往往需要自定义实现以满足特定需求。本文将详细介绍如何在Unity3D中自定义Debug双击溯…...

环境搭建-Docker搭建ClickHouse
Docker搭建ClickHouse 一、前言二、ClickHouse安装2.1 拉取镜像运行ClickHouse服务 三、测试安装3.1 进入clickhouse容器3.2 命令补充说明 四、测试连接五、设置CK的用户名密码 一、前言 本文使用的Docker使用Windows搭建,Linux版本的搭建方式一样。 Windows系统搭…...
)
深入理解CSS中的变量(概念篇)
CSS变量,也称为自定义属性,是一种在CSS中定义和重用值的方式。它们允许开发者在一个地方定义样式值,然后在整个样式表中引用这些值,从而提高代码的可维护性和可读性。 1、定义和使用CSS变量 CSS变量的定义和使用非常简单。变量名以两个连字符开头,变量值为任何有效的CSS…...
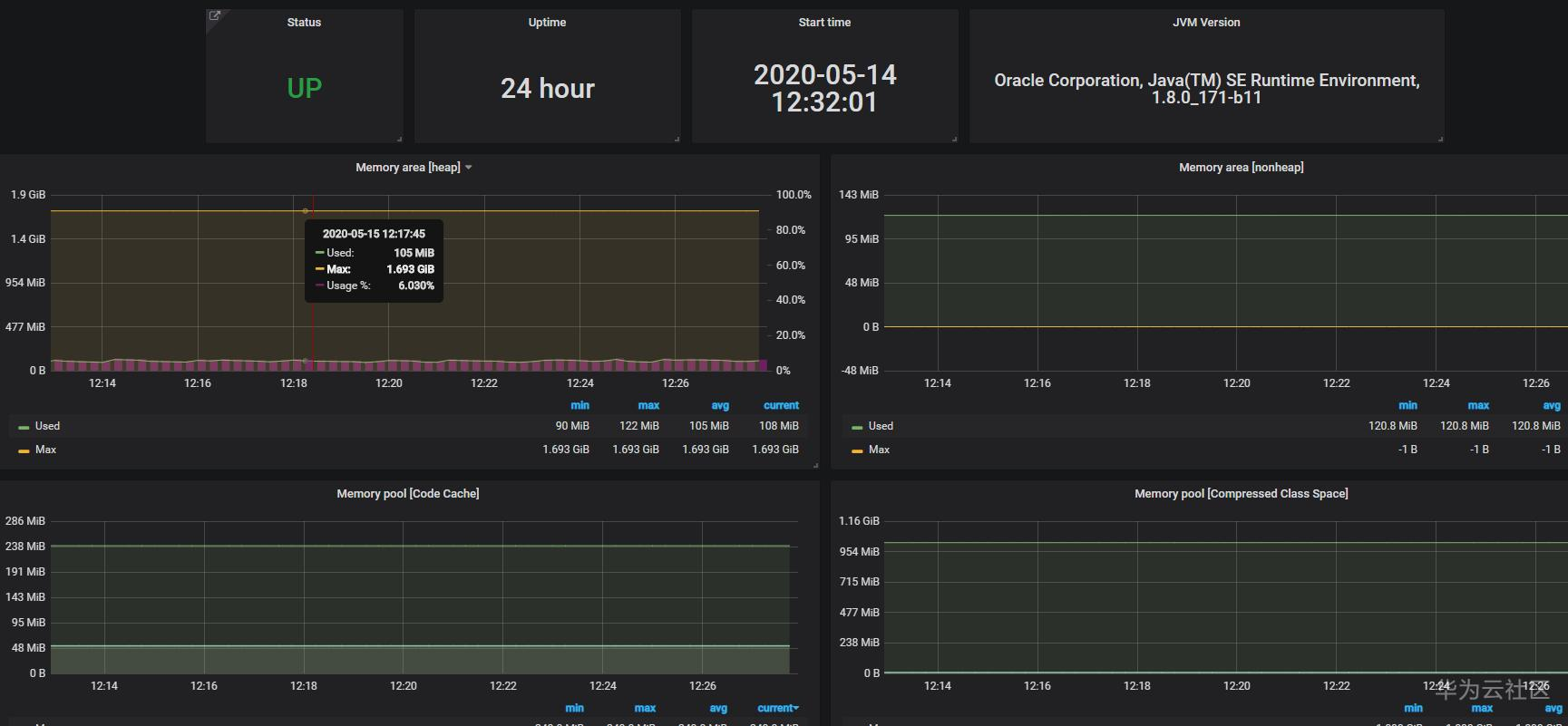
Prometheus 监控Tomcat等java应用的状态
5月应用服务出现问题,当别的小伙伴问我,有没有Tomcat等应用状态的监控的时候,我有点儿尴尬。所以赶紧抽空部署一下。 在配置之前,就当已经会安装jdk和tomcat了。 一、下载jmx_exporter #linux下 cd /usr/local/prometheus wget …...
和背包问题(Knapsack Problem))
c++中的斐波那契数列(Fibonacci Sequence)和背包问题(Knapsack Problem)
前言 hello,大家好啊,我是文宇,不是文字,是文宇哦。 斐波那契数列(Fibonacci Sequence) 斐波那契数列(Fibonacci Sequence)是一个经典的数学问题,其中每个数都是前两个…...

connect的非阻塞模式
本文参考:connect 函数在阻塞和非阻塞模式下的行为 一般情况下,在使用connect连接服务端时,需要等待一会儿才会函数才会返回,导致程序阻塞。为了降低阻塞的影响,我们可能会单独开个线程处理connect请求,例…...

jenkins面试题全集
1. 简述什么是Jenkins ? Jenkins是一个开源的持续集成的服务器,Jenkins开源帮助我们自动构建各类项目。 Jenkins强大的插件式,使得Jenkins可以集成很多软件,可以帮助我们持续集成我们的工程项目,对于我们测试来说&…...

Python中最好学和最实用的有哪些库和框架
Python拥有丰富的库和框架,这些库和框架覆盖了从数据处理、科学计算、Web开发到机器学习等多个领域。以下是一些值得学习的Python库和框架: 数据处理与科学计算 NumPy 描述:NumPy是Python中用于科学计算的一个库,它提供了一个强…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
