6.乳腺癌良性恶性预测(二分类、逻辑回归、PCA降维、SVD奇异值分解)
乳腺癌良性恶性预测
- 1. 特征工程
- 1.1 特征筛选
- 1.2 特征降维 PCA
- 1.3 SVD奇异值分解
- 2. 代码
- 2.1 逻辑回归、二分类问题
- 2.2 特征降维 PCA
- 2.3 SVD奇异值分解
1. 特征工程
- 专业上:30个人特征来自于临床一线专家,每个特征和都有医学内涵;
- 数据上:30个中可能有一些是冗余的。
1.1 特征筛选
- 从30个选出重要的,踢掉不重要的。
- 从数据的角度来讲,不建议进行特征筛选,做特征筛选可能只是为了解释性,给领导看看而已。因为再不重要的特征都有信息,筛选掉必然导致信息的丢失。
- 线性回归的系数代表该项特征的重要性,系数就代表权重。
- 使用协方差或皮尔逊系数判断两列特征的相关性。
1.2 特征降维 PCA
- 把原来30个特征中的核心信息中抽取出来,融合到新生成的几个特征中,新的特征不是原来的任何一个!
- PCA(Principal Component Analysis,主成分分析)
1.3 SVD奇异值分解
- SVD(奇异值分解)是一种在信号处理、统计学、机器学习等领域广泛应用的矩阵分解方法。
- 它可以将一个矩阵分解为三个特定的矩阵的乘积,这三个矩阵分别是:一个正交矩阵、一个对角矩阵(其元素为奇异值,且按从大到小排列)以及另一个正交矩阵的转置。
2. 代码
2.1 逻辑回归、二分类问题
y = F ( X ) = s i g m o i d ( x 0 w 0 + x 1 w 1 + x 2 w 2 + . . . + x 12 w 12 ) y=F(X)=sigmoid(x_0w_0+x_1w_1+x_2w_2+...+x_{12}w_{12}) y=F(X)=sigmoid(x0w0+x1w1+x2w2+...+x12w12)
from sklearn.datasets import load_breast_cancer
X,y=load_breast_cancer(return_X_y=True)
print(X.shape,y.shape) #:(569, 30) (569,)from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y)
# 逻辑回归,实际是二分类,就是线性回归加了一个激活函数 sigmoid
from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(max_iter=10000)
lr.fit(X_train,y_train)
pred=lr.predict(X_test)
acc=(pred==y_test).mean()
print(acc)
2.2 特征降维 PCA
# 特征降维 PCA(主成分分析)
from sklearn.decomposition import PCA
pca = PCA(n_components=20)
pca.fit(X_train)
X_train1 = pca.transform(X_train)
# 原始数据
lr = LogisticRegression(max_iter=10000)
lr.fit(X_train,y_train)
(lr.predict(X_test)==y_test).mean() #:0.965034965034965
# 10个特征
lr1 = LogisticRegression(max_iter=10000)
# 特征降维
# 1. 构建
pca=PCA(n_components=10)
# 2. 拟合
pca.fit(X_train)
# 3. 转换
X_train1 = pca.transform(X_train)
X_test1 = pca.transform(X_test)lr1.fit(X_train1,y_train)
(lr1.predict(X_test1)==y_test).mean() #:0.958041958041958
2.3 SVD奇异值分解
import numpy as np
from matplotlib import pyplot as plt
beauty = plt.imread(fname="beauty.jpg")
# [Height, Width, Channel]
print(beauty.shape) #:(627, 481, 3)
r=beauty[:,:,0]
plt.imshow(r,cmap='gray')

U, S, V = np.linalg.svd(a=r, full_matrices=False)
print(U.shape,S.shape, V.shape) #: (627, 481) (481,) (481, 481)
plt.plot(S)

"""降维之后的效果
"""
K = 20
restore = U[:,:K] @ np.diag(S[:K]) @ V[:K, :]
plt.imshow(X=restore, cmap="gray")

相关文章:

6.乳腺癌良性恶性预测(二分类、逻辑回归、PCA降维、SVD奇异值分解)
乳腺癌良性恶性预测 1. 特征工程1.1 特征筛选1.2 特征降维 PCA1.3 SVD奇异值分解 2. 代码2.1 逻辑回归、二分类问题2.2 特征降维 PCA2.3 SVD奇异值分解 1. 特征工程 专业上:30个人特征来自于临床一线专家,每个特征和都有医学内涵;数据上&…...
)
Vue3响应式高阶用法之markRaw()
Vue3响应式高阶用法之markRaw() 文章目录 Vue3响应式高阶用法之markRaw()一、简介二、使用场景2.1 避免性能开销2.2 防止意外修改 三、基本使用3.1 标记对象 四、功能详解4.1 markRaw与reactive的区别4.2 markRaw与ref的区别 五、最佳实践及案例5.1 使用大型第三方库对象5.2 静…...
免费SSL证书的安全性与获取指南
SSL证书是一种数字凭证,用于加密用户与网站之间的信息交换,以确保传输的数据不被第三方窃取。它像是一个数字版的密封印章,为数据的传输过程提供了一层保护膜。 免费的SSL证书通常由CA机构提供,它们同样可以提供基础数据的加密服…...

【CN】Argo 持续集成和交付(一)
1.简介 Argo 英 [ˈɑ:ɡəu] 美 [ˈɑrˌɡo] Kubernetes 原生工具,用于运行工作流程、管理集群以及正确执行 GitOps。 Argo 于 2020 年 3 月 26 日被 CNCF 接受为孵化成熟度级别,然后于 2022 年 12 月 6 日转移到毕业成熟度级别。 argoproj.github.i…...

Unity3D 自定义Debug双击溯源问题详解
前言 在Unity3D的开发过程中,经常需要处理各种交互和事件,其中双击事件是常见的需求之一。然而,由于Unity自带的双击检测机制并不完善,开发者往往需要自定义实现以满足特定需求。本文将详细介绍如何在Unity3D中自定义Debug双击溯…...

环境搭建-Docker搭建ClickHouse
Docker搭建ClickHouse 一、前言二、ClickHouse安装2.1 拉取镜像运行ClickHouse服务 三、测试安装3.1 进入clickhouse容器3.2 命令补充说明 四、测试连接五、设置CK的用户名密码 一、前言 本文使用的Docker使用Windows搭建,Linux版本的搭建方式一样。 Windows系统搭…...
)
深入理解CSS中的变量(概念篇)
CSS变量,也称为自定义属性,是一种在CSS中定义和重用值的方式。它们允许开发者在一个地方定义样式值,然后在整个样式表中引用这些值,从而提高代码的可维护性和可读性。 1、定义和使用CSS变量 CSS变量的定义和使用非常简单。变量名以两个连字符开头,变量值为任何有效的CSS…...
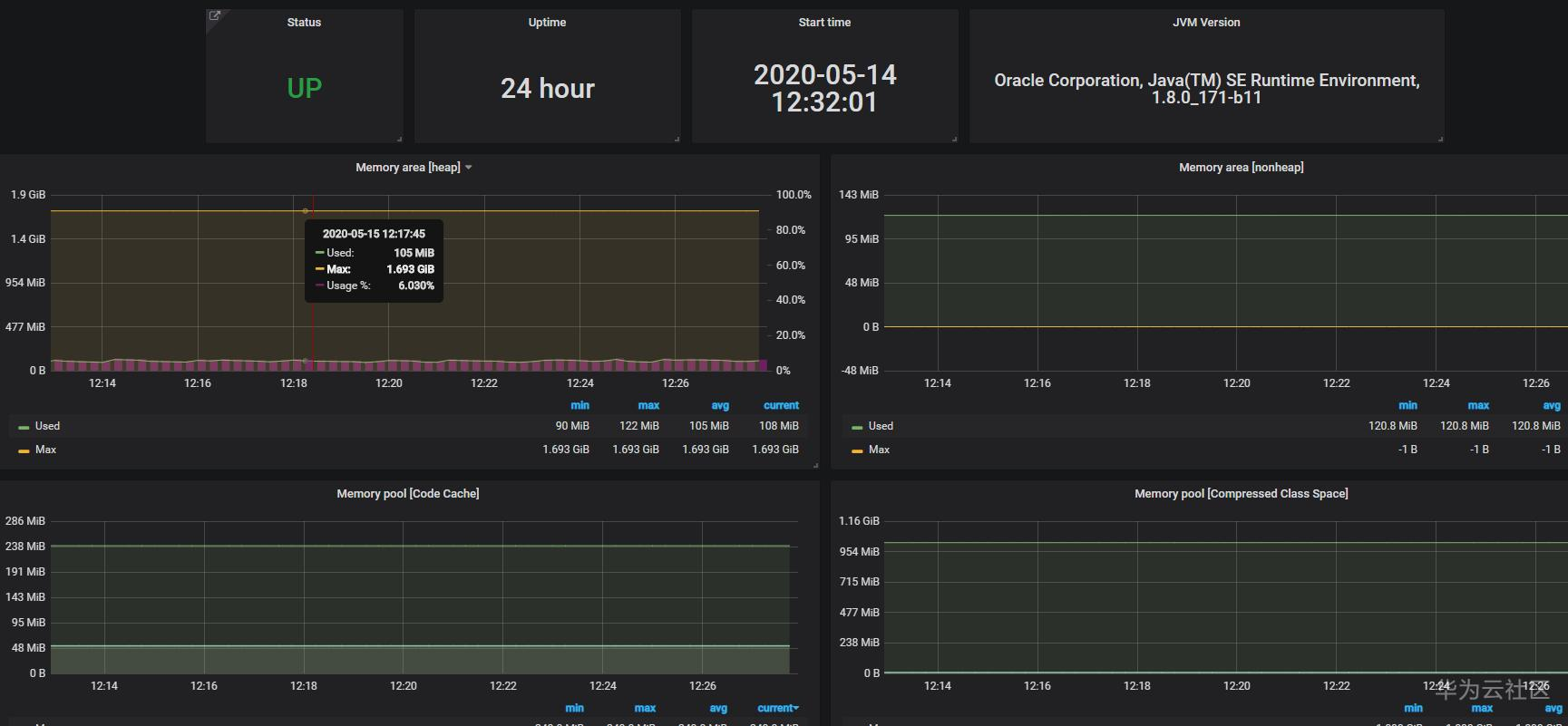
Prometheus 监控Tomcat等java应用的状态
5月应用服务出现问题,当别的小伙伴问我,有没有Tomcat等应用状态的监控的时候,我有点儿尴尬。所以赶紧抽空部署一下。 在配置之前,就当已经会安装jdk和tomcat了。 一、下载jmx_exporter #linux下 cd /usr/local/prometheus wget …...
和背包问题(Knapsack Problem))
c++中的斐波那契数列(Fibonacci Sequence)和背包问题(Knapsack Problem)
前言 hello,大家好啊,我是文宇,不是文字,是文宇哦。 斐波那契数列(Fibonacci Sequence) 斐波那契数列(Fibonacci Sequence)是一个经典的数学问题,其中每个数都是前两个…...

connect的非阻塞模式
本文参考:connect 函数在阻塞和非阻塞模式下的行为 一般情况下,在使用connect连接服务端时,需要等待一会儿才会函数才会返回,导致程序阻塞。为了降低阻塞的影响,我们可能会单独开个线程处理connect请求,例…...

jenkins面试题全集
1. 简述什么是Jenkins ? Jenkins是一个开源的持续集成的服务器,Jenkins开源帮助我们自动构建各类项目。 Jenkins强大的插件式,使得Jenkins可以集成很多软件,可以帮助我们持续集成我们的工程项目,对于我们测试来说&…...

Python中最好学和最实用的有哪些库和框架
Python拥有丰富的库和框架,这些库和框架覆盖了从数据处理、科学计算、Web开发到机器学习等多个领域。以下是一些值得学习的Python库和框架: 数据处理与科学计算 NumPy 描述:NumPy是Python中用于科学计算的一个库,它提供了一个强…...

文件解析的终极工具:Apache Tika
文件解析的终极工具:Apache Tika Apache Tika 简介 Apache Tika 是一个开源的、跨平台的库,用于检测、提取和解析各种类型文件的元数据。 它支持多种文件格式,包括文档、图片、音频和视频。 Tika是一个底层库,经常用于搜索引擎…...

Hadoop 重要监控指标
某安卓逆向课程打包下载(92节课) https://pan.quark.cn/s/53cec8b8055a 某PC逆向课程(100节课打包下载) https://pan.quark.cn/s/e38f2b24f36c Hadoop 是一个开源的分布式存储和计算框架,广泛应用…...

oracle 查询锁表
oracle 查询锁表 SELECT o.object_name, s.sid, s.serial#, p.spid, s.username, s.program FROM v l o c k e d o b j e c t l J O I N d b a o b j e c t s o O N l . o b j e c t i d o . o b j e c t i d J O I N v locked_object l JOIN dba_objects o ON l.object_id …...

进程概念(三)----- fork 初识
目录 前言1. pid && ppid2. forka. 为什么 fork 要给子进程返回 0, 给父进程返回子进程的 pid ?b. 一个函数是如何做到两次的?c. fork 函数在干什么?d. 一个变量怎么做到拥有不同的内容的?e. 拓展:…...

huawei 路由 RIP 协议中三种定时器的工作原理
RFC2453 定义的三种 RIP 协议定时器 更新定时器(Update Timer):用于触发更新报文的发送,超时时间为 30 秒。老化定时器(Age Timer):如果在老化时间内没有收到邻居发送的响应报文,则…...

HTML常见标签——超链接a标签
一、a标签简介 二、a标签属性 href属性 target属性 三、a标签的作用 利用a标签进行页面跳转 利用a标签返回页面顶部以及跳转页面指定区域 利用a标签实现文件下载 一、a标签简介 <a>标签用于做跳转、导航,是双标签,记作<a></a>&#…...

Python 爬虫入门(一):从零开始学爬虫 「详细介绍」
Python 爬虫入门(一):从零开始学爬虫 「详细介绍」 前言1.爬虫概念1.1 什么是爬虫?1.2 爬虫的工作原理 2. HTTP 简述2.1 什么是 HTTP?2.2 HTTP 请求2.3 HTTP 响应2.4 常见的 HTTP 方法 3. 网页的组成3.1 HTML3.2 CSS3.…...

Linux嵌入式学习——数据结构——概念和Seqlist
数据结构 相互之间存在一种或多种特定关系的数据元素的集合。 逻辑结构 集合,所有数据在同一个集合中,关系平等。 线性,数据和数据之间是一对一的关系。数组就是线性表的一种。 树, 一对多 图,多对多 …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
