算法竞赛必考算法——动态规划(01背包和完全背包)
动态规划(一)

目录
- 动态规划(一)
- 1.01背包问题
- 1.1题目介绍
- 1.2思路一介绍(二维数组)
- 1.3思路二介绍(一维数组) ==空间优化==
- 1.4思路三介绍(输入数据优化)
- 2.完全背包问题
- 2.1题目描述:
- 2.2思路一(朴素算法)
- 2.3思路二(将k优化处理掉)
- 2.4思路三(优化j的初始条件)
- 总结

1.01背包问题
1.1题目介绍

1.2思路一介绍(二维数组)

代码如下:
#include<iostream>
#include<algorithm>
using namespace std;const int N=1010;int v[N],w[N]; //v[N]是物品体积 w[N]是物品的价值int f[N][N]; //f[i][j]在体积不超j的前提下,从i个物品中选择最大值int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])//如果我们的背包容量j大于第i个物品的体积,我们在进行决策是否加入第i个物品f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;return 0;}
1.3思路二介绍(一维数组) 空间优化
为什么可以使用一维数组?
我们先来看一看01背包问题的状态转移方程,我们可以发现 f[i]只用到了f[i-1],其他的是没有用到的,我们可以用滚动数组来做。
还有一个原因就是我们在计算f[i] [j]的时候我们只用到了f[i-1] [j]和f[i-1] [j-v[i]],其中j和j-v[i]都是小于等于j的,在j的同一侧,所以我们综合以上两点原因就可以将二维优化到一维,即完成空间优化。

我们先来将二维和优化后的一维在关键算法代码上进行一下对比:
for(int i = 1; i <= n; i++) for(int j = m; j >= 0; j--){if(j < v[i]) f[i][j] = f[i - 1][j]; // 优化前f[j] = f[j]; // 优化后,该行自动成立,可省略。else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); // 优化前f[j] = max(f[j], f[j - v[i]] + w[i]); // 优化后}
实际上,只有当枚举的背包容量 >= v[i] 时才会更新状态,因此我们可以修改循环终止条件进一步优化。
for(int i=1;j<=n;i++)
{for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]);}
}

#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
int v[N], w[N];
int f[N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++ )for (int j = m; j >= v[i]; j -- )f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;
}
1.4思路三介绍(输入数据优化)
我们注意到在处理数据时,我们是一个物品一个物品,一个一个体积的枚举。因此我们可以不必开两个数组记录体积和价值,而是边输入边处理。
#include<bits/stdc++.h>using namespace std;const int MAXN = 1005;
int f[MAXN]; // int main()
{int n, m; cin >> n >> m;for(int i = 1; i <= n; i++) {int v, w;cin >> v >> w; // 边输入边处理for(int j = m; j >= v; j--)f[j] = max(f[j], f[j - v] + w);}cout << f[m] << endl;return 0;
}

2.完全背包问题
2.1题目描述:

2.2思路一(朴素算法)
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[n][m]<<endl;return 0;
}
上述朴素算法和01背包问题的朴素算法非常相似,但是会超时。所以我们接下来就会对这个算法进行优化处理。
2.3思路二(将k优化处理掉)

我们先来分析一下状态转移方程,我们发现方程一和方程二有一定的联系,我们先不看方程一红色圈出来的部分,我们比较方程一黄色的部分和方程二的内容,我们发现方程一就是比方程二每一项多了一个w,那么我们黄色圈出来的部分的最大值也就比方程二的最大值多w,那么我们其实就可以将方程一圈出来黄色的部分进行等价替换,替换成红色方框黄色字体的内容,我们最终得出最下方的结论,其实我们要求得最大值之和两个状态有关,比较它们的最大值即可。
我们发现好像最后的状态转移方程和k并没有关系了,那么我们就干脆去掉k的那次循环
所以我们对核心代码进行了优化:
for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{f[i][j] = f[i-1][j];//状态一,即不取第i个物品if(j-v[i]>=0)//判断是否可以加入第i个物品f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//状态二
}
完整代码如下:
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int n,m;
int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i]){f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}}cout<<f[n][m]<<endl;return 0;
}
我们来比较一个完全背包的核心代码和01背包核心代码的区别:
//01背包问题核心优化后代码
for(int i=1;i<=n;i++)
{for(int j=m;j>=v[i];j--){ f[i][j]=f[i-1][j];if(j>=v[i]){f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}}
}
//完全背包问题核心优化后代码
for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{f[i][j] = f[i-1][j];//状态一,即不取第i个物品if(j-v[i]>=0)//判断是否可以加入第i个物品f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);//状态二
}
我们发现其实本质也就是一句不同:注意i的下标

我们这个i的下标是根据两个不同的背包问题的状态转移方程得出来的,我们01背包问题因为要使用第i-1层的数据,所以我们枚举j的时候只能从后往前枚举,这样做是因为j-v[i]小于j,那么f[j-v[i]]的数据就会被改,那么我们使用的数据其实就是第i层的数据了,不满足状态转移方程,所以我们要从后往前枚举,但是完全背包问题使用的就是第i层的数据,所以不存在从前往后枚举就会在使用前数据就发生意外改变的这种情况,所以就在这个地方这两个核心算法略有差别。
2.4思路三(优化j的初始条件)
这个和01背包问题的优化方法是一样的,就不多赘述了。
核心代码如下:
for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++)//注意了,这里的j是从小到大枚举,和01背包不一样{f[j] = max(f[j],f[j-v[i]]+w[i]);}
完整代码如下:
#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{int n,m;cin>>n>>m;for(int i = 1 ; i <= n ;i ++){cin>>v[i]>>w[i];}for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++){f[j] = max(f[j],f[j-v[i]]+w[i]);}cout<<f[m]<<endl;
}
总结
本篇博客主要涉及动态规划背包问题的01背包问题和完全背包问题,给大家分享了实现的思路和代码模板,大家也可以看看yxc的背包九讲,图片转载于yxc,希望对大家有所帮助,后面会持续更新~
相关文章:

算法竞赛必考算法——动态规划(01背包和完全背包)
动态规划(一) 目录动态规划(一)1.01背包问题1.1题目介绍1.2思路一介绍(二维数组)1.3思路二介绍(一维数组) 空间优化1.4思路三介绍(输入数据优化)2.完全背包问题2.1题目描述:2.2思路一(朴素算法)2.3思路二(将k优化处理掉)2.4思路三(优化j的初始条件)总结1.01背包问题…...
基于深度学习的农作物叶片病害检测系统(UI界面+YOLOv5+训练数据集)
摘要:农作物叶片病害检测系统用于智能检测常见农作物叶片病害情况,自动化标注、记录和保存病害位置和类型,辅助作物病害防治以增加产值。本文详细介绍基于YOLOv5深度学习模型的农作物叶片病害检测系统,在介绍算法原理的同时&#…...
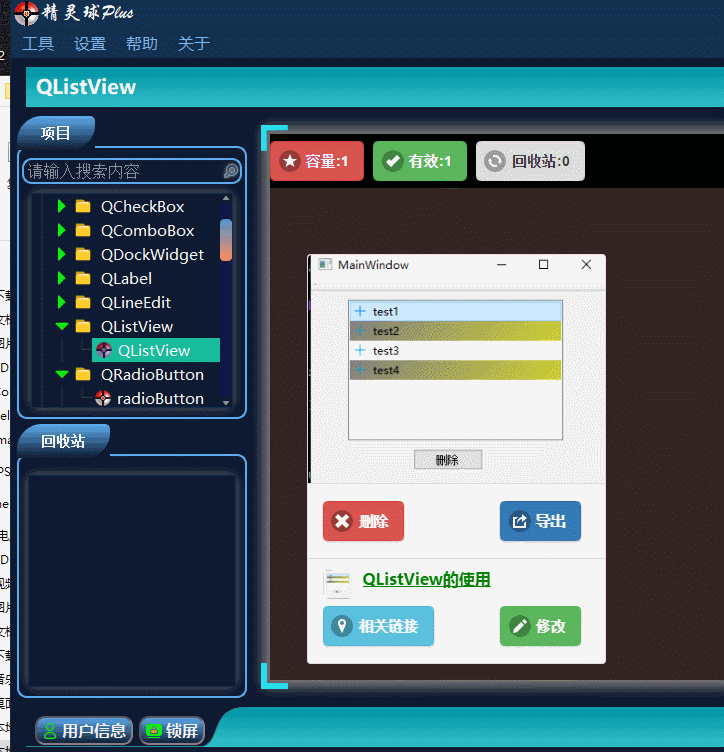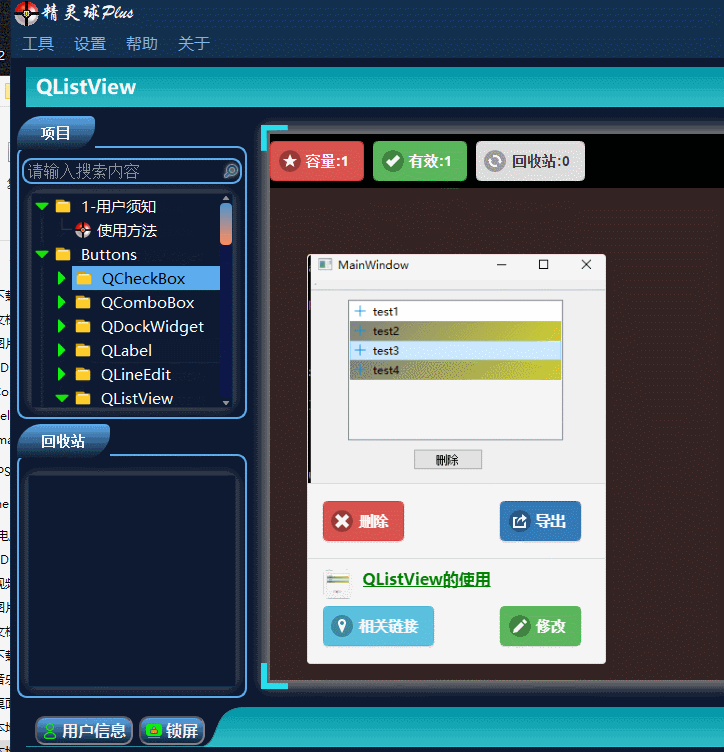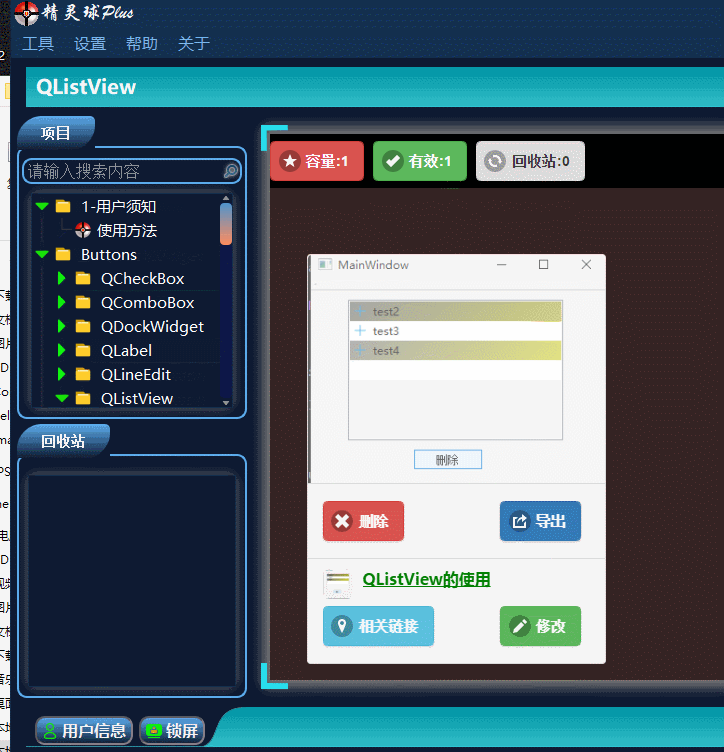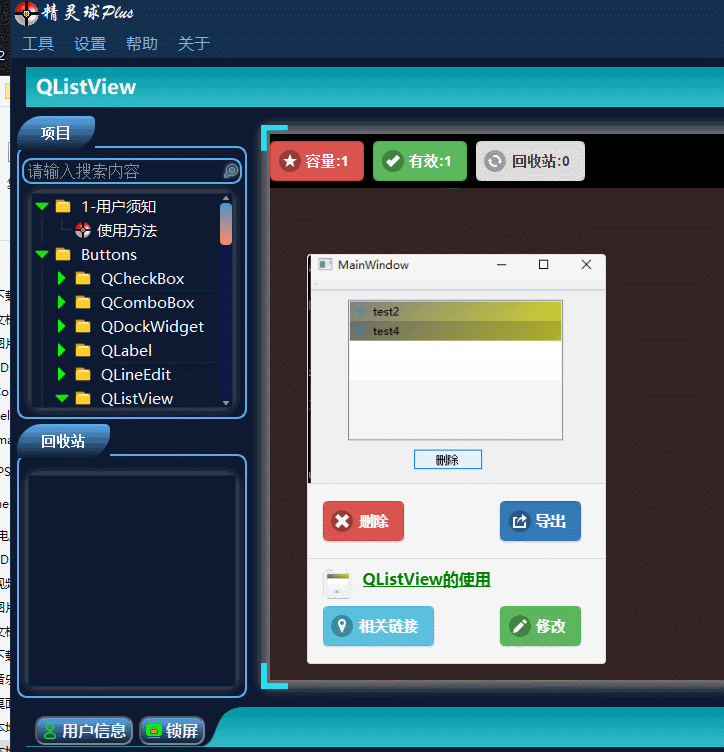
QT入门Item Views之QListView
目录 一、QListView界面相关 1、布局介绍 二、代码展示 1、创建模型,导入模型 2、 设置隔行背景色 3、删除选中行 三、源码下载 此文为作者原创,创作不易,转载请标明出处! 一、QListView界面相关 1、布局介绍 先看下界面…...
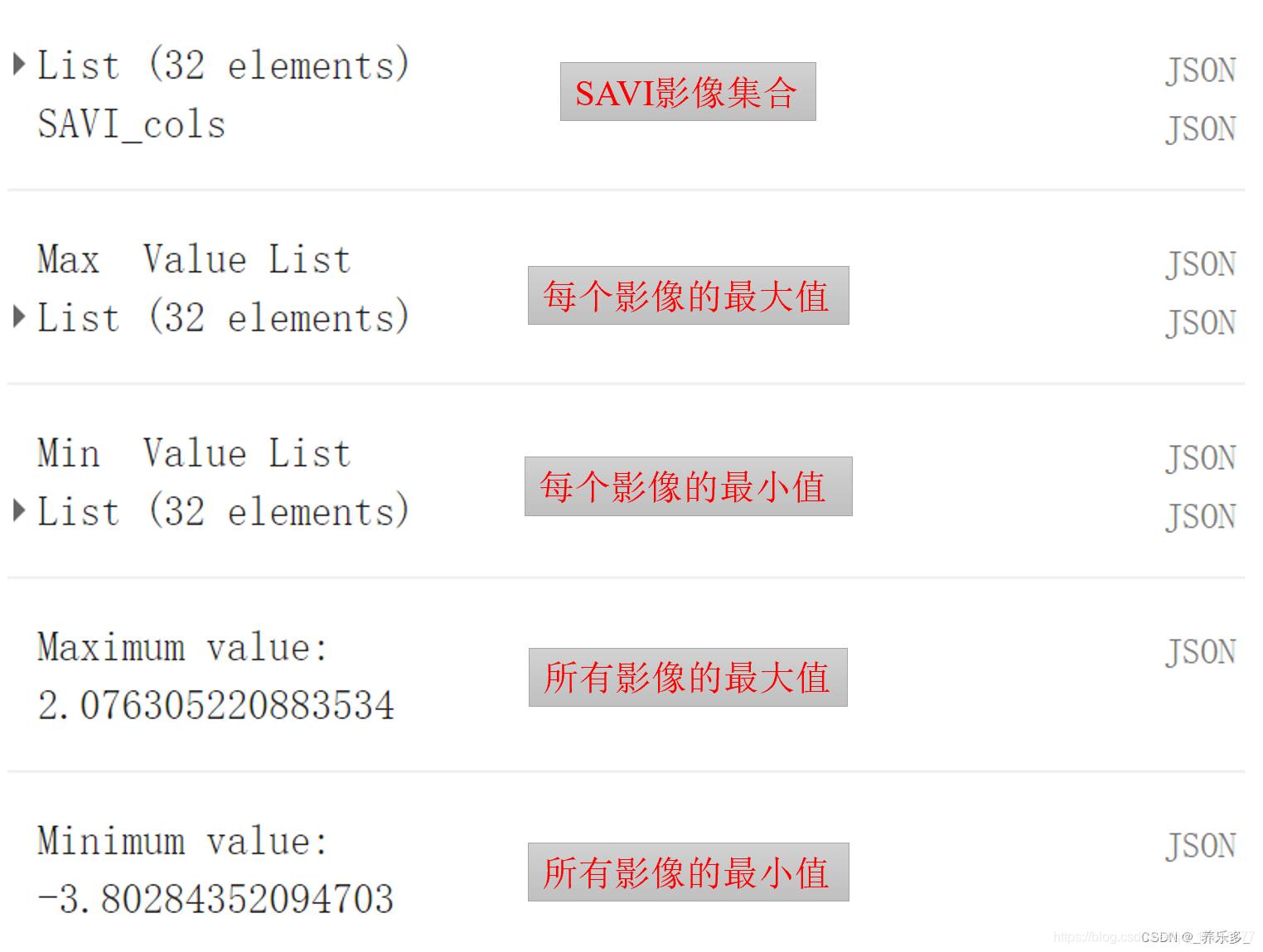
GEE:计算1990-2021年的指数最大值和最小值,并根据最大最小值对每一副影像归一化
本文记录了在GEE平台上计算影像集合中所有像素的最大值和最小值。并且根据该最大最小值对所有影像进行最大最小值归一化。以SAVI为例,记录了主要函数的使用方法和代码。 结果如图所示, 文章目录 一、计算每一副影像的最大值或者最小值,并将最值保存在 List 中二、计算 Lis…...

LeetCode KMP 算法
可以参考https://www.bilibili.com/video/BV1AY4y157yL/kmp 主要做的就是子串匹配,类似C程序的 strstr() 函数记录一下,也防止我自己忘记传统暴力求解算法是源串 ssssssssa 子串 sssa(下面暴力求解) 先 (子串从 0 位置匹配&#x…...

全面剖析OpenAI发布的GPT-4比其他GPT模型强在哪里
最强的文本生成模型GPT-4一、什么是GPT-4二、GPT-4的能力三、和其他GPT模型比较3.1、增加了图像模态的输入3.2、可操纵性更强3.3、复杂任务处理能力大幅提升3.4、幻觉、安全等局限性的改善3.6、风险和缓解措施改善更多安全特性3.7、可预测的扩展四、与之前 GPT 系列模型比较五、…...
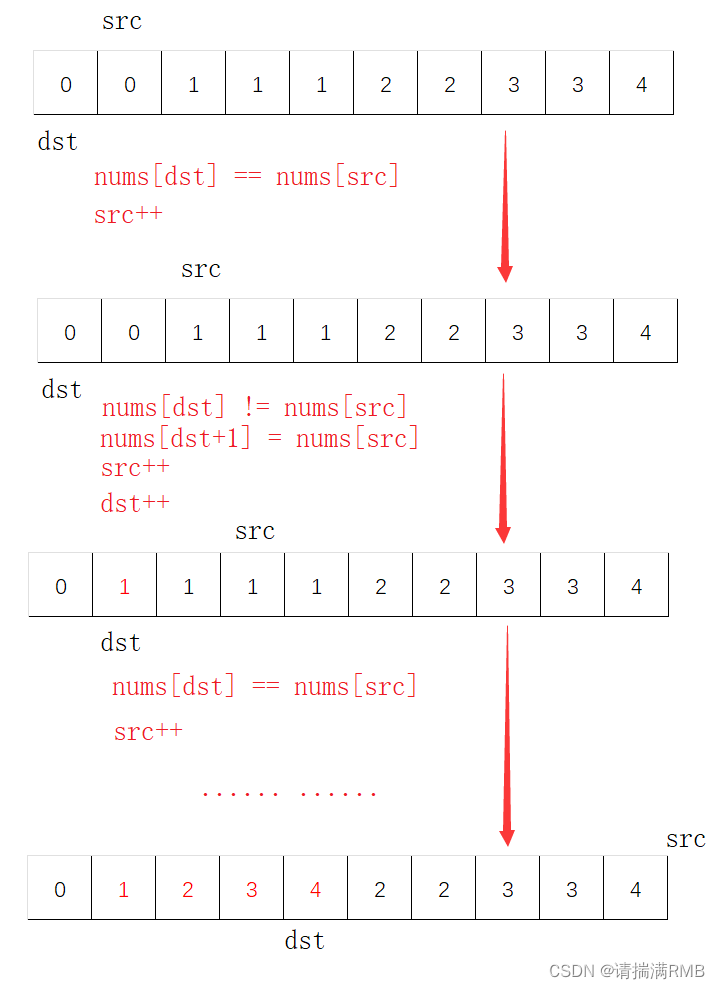
leetcode——26. 删除有序数组中的重复项
文章目录🐨1. 题目🏹2. 思路🪃3. 代码实现🐨1. 题目 给你一个升序排列的数组nums,请你原地删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。元素的相对顺序应该保持一致。 由…...
基于springboot垃圾分类网站设计实现【毕业论文、源码】
摘要本论文主要论述了如何使用JAVA语言开发一个垃圾分类网站,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述垃圾分类网站的当前背景以及系统开发的目的&#x…...
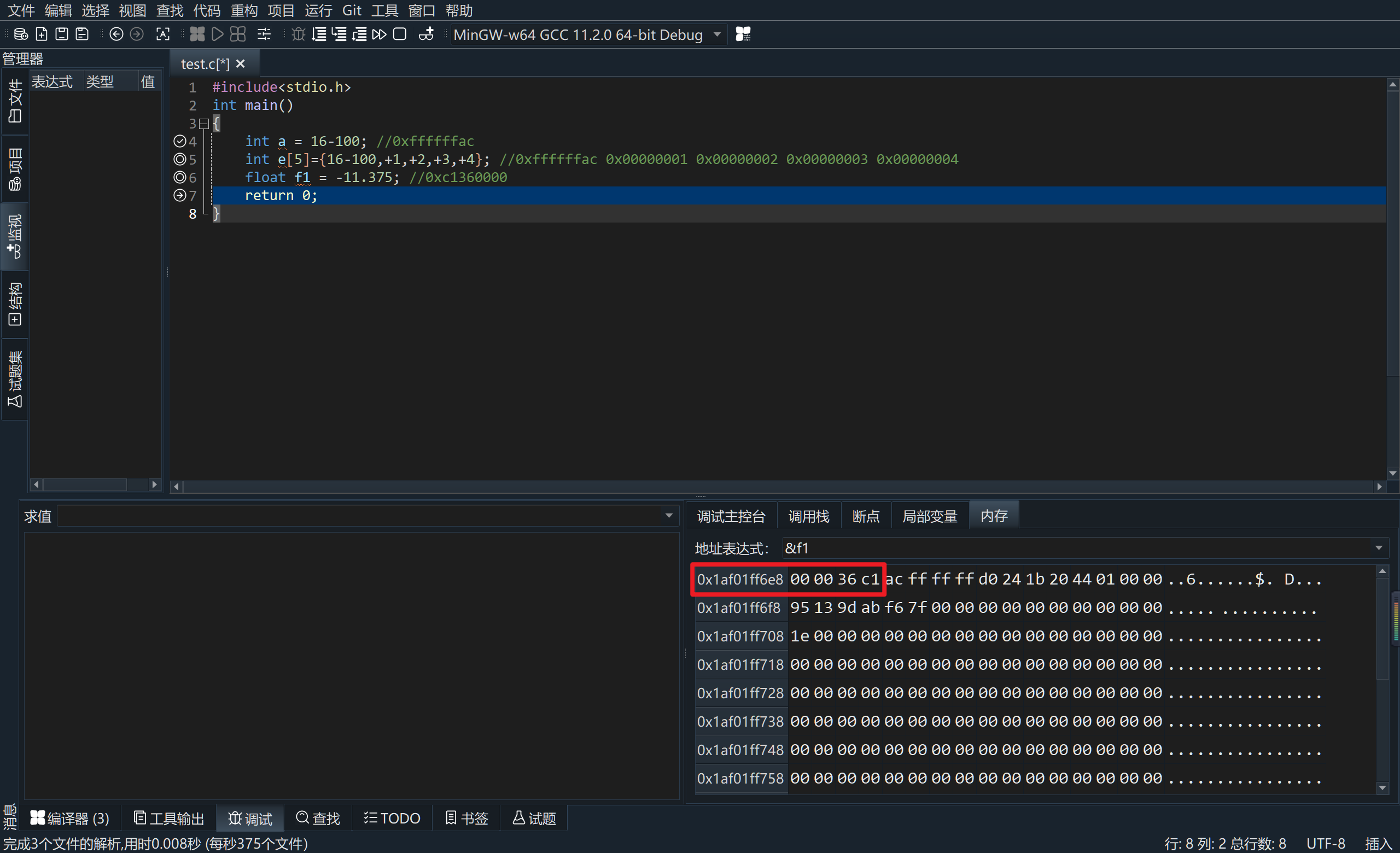
计算机组成原理实验一(完整)
在VC中使用调试功能将下列语句运行的内存存放结果截图,每运行一句需截图一次。 #include<stdio.h> int main() {int a 你的学号末两位-100; //0x????????&#x…...

【SSM】MyBatis(一.基础)
文章目录1.ORM2. 数据库表3. 入门程序3.1 创建项目3.2 开发3.3 一个比较完整规格的mybatis程序3.4 测试案例 junit3.5 对第一个mybatis使用junit测试3.6 集成日志框架logback3.7mybatis工具类编写1.ORM Object(JVM中的Java对象) Relational(关系型数据库) Mapping(映射) mybat…...
LInux指令之文件目录类
文章目录一、帮助指令二、文件目录类ls指令cd指令 (切换目录)mkdir指令(创建目录)rmdir指令(删除目录)touch指令(创建空文件)cp指令(拷贝文件)rm指令mv指令cat指令(查看)more指令les…...
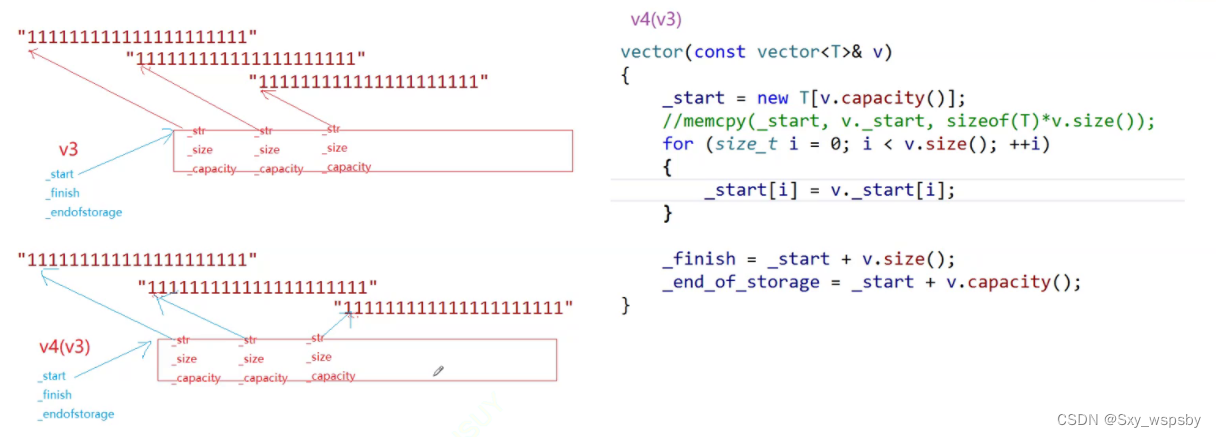
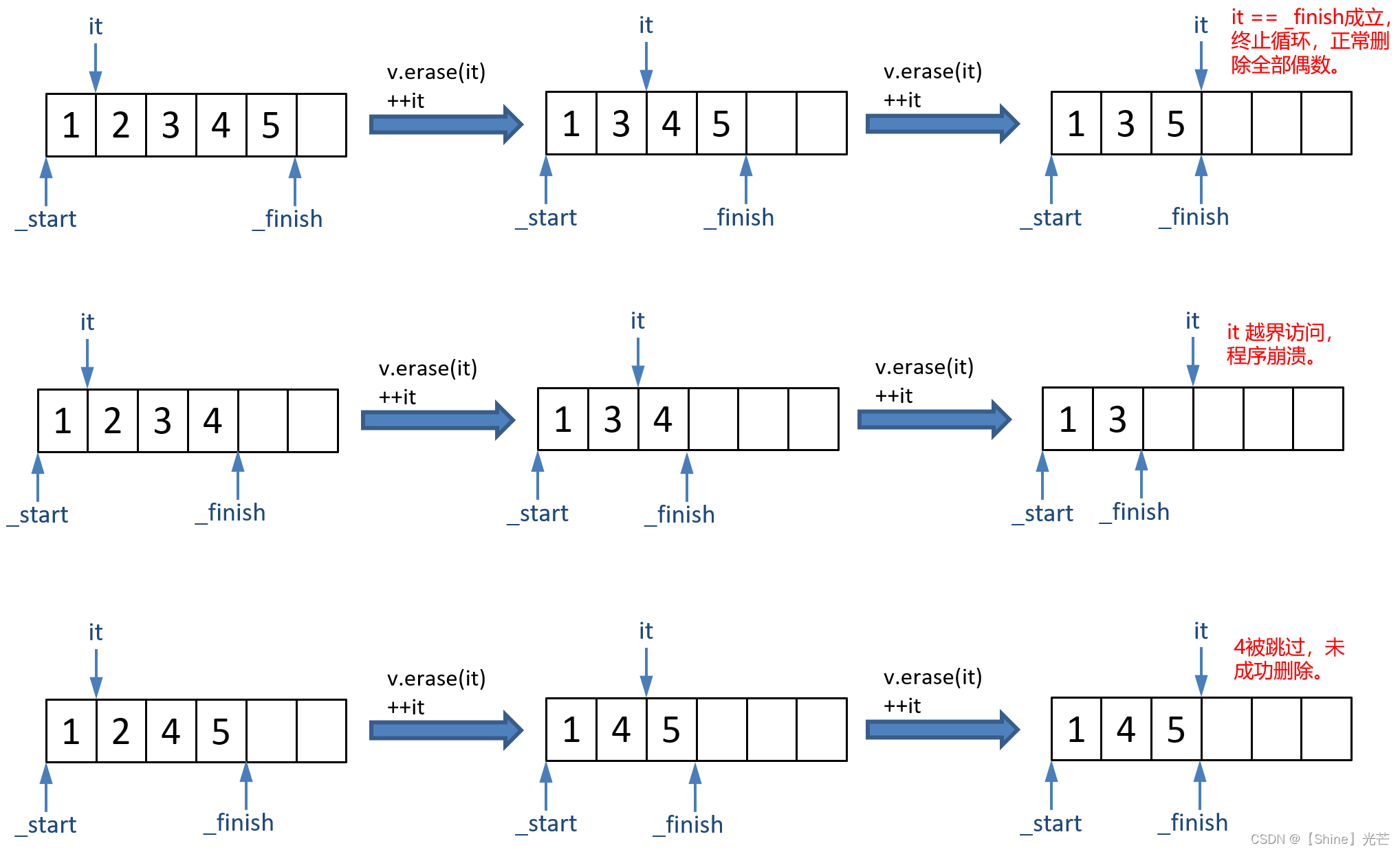
【c++】:STL中vector的模拟使用及模拟实现
文章目录 前言一.使用库中vector常用接口二.vector的模拟实现总结前言 上一篇我们讲解了STL中的string的使用和模拟实现,这次我们就来讲解STL中的vector,vector相对于string来说模拟实现会难一些,难点在于迭代器失效问题和深浅拷贝问题。 首…...
C++ STL:vector的使用方法及模拟实现
目录 一. vector概述 二. vector接口函数的使用方法和模拟实现 2.1 vector类模板的成员变量 2.2 构造函数的使用和模拟实现 2.2.1 构造函数的使用方法 2.2.2 构造函数的模拟实现 2.3 析构函数的模拟实现 2.4 赋值运算符重载函数的使用和模拟实现 2.4.1 函数的使用 2.…...

naive UI 的upload组件自定义手动上传图片的base64位
<template><n-upload ref"uploadRef" action"#" :default-upload"false" :custom-request"myUpload"><n-button>点击选择文件</n-button></n-upload><n-button click"submitUpload"> 上…...
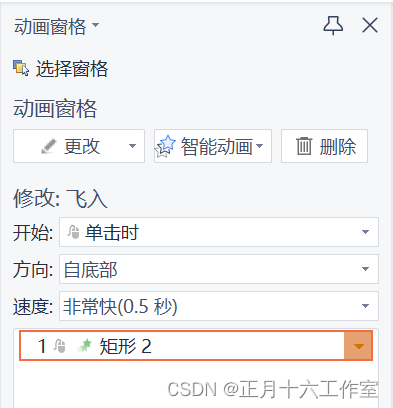
信创办公–基于WPS的PPT最佳实践系列(表格和图标常用动画)
信创办公–基于WPS的PPT最佳实践系列(表格和图标常用动画) 目录应用背景操作步骤图表常用动画效果:擦除效果表格常用动画效果:轮子效果应用背景 文不如表,表不如图。在平时用ppt做总结时,我们会经常用到图…...
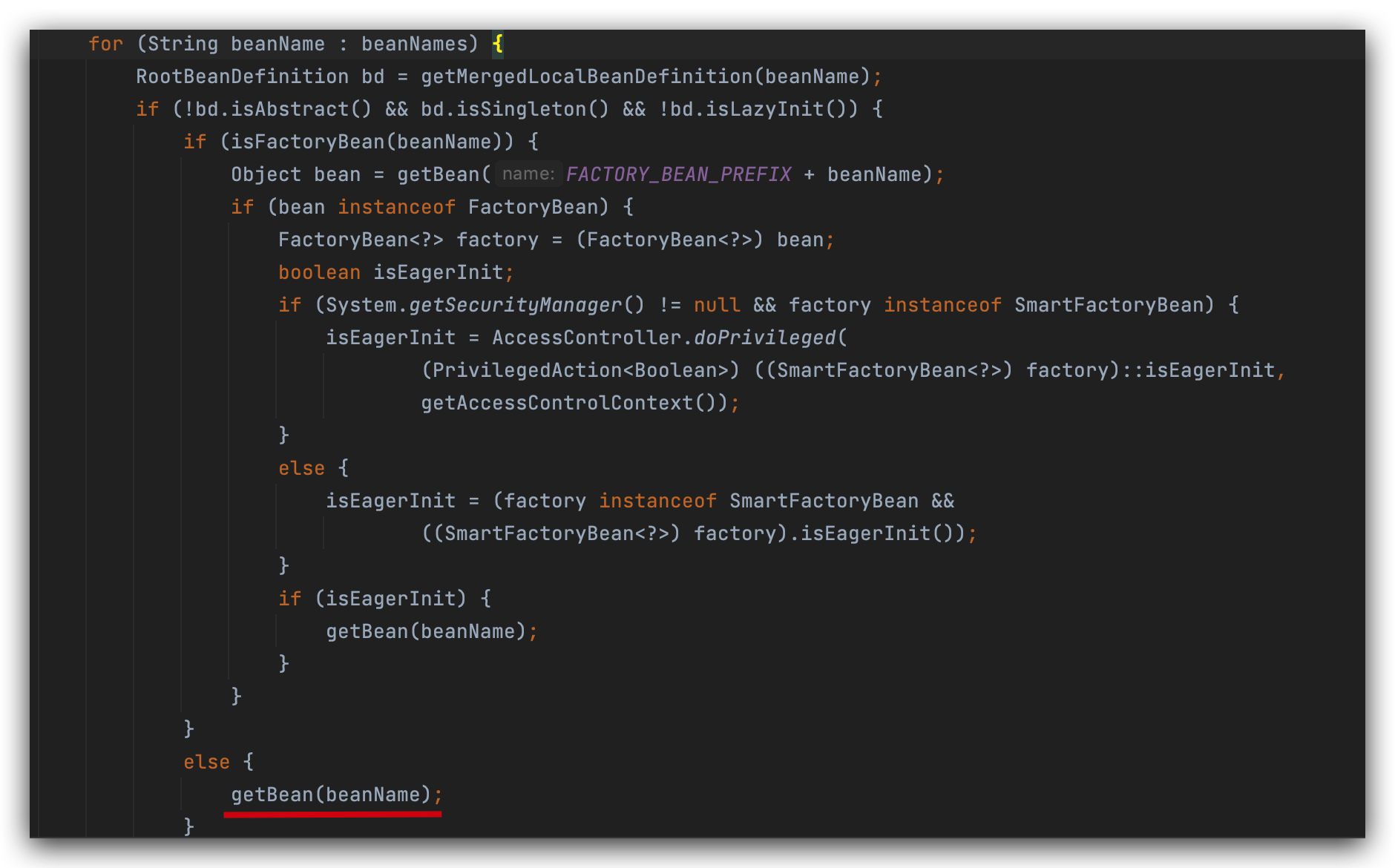
Spring Bean实例化和初始化的过程
承接上文Spring Bean生命周期应用程序在运行过程中能否去读取当前系统的环境变量或系统属性?这里涉及到一个非常重要的接口Environment,System.getenv,System.getProperties都是获取当前系统环境变量,Environment接口的实现类AbstractEnviro…...
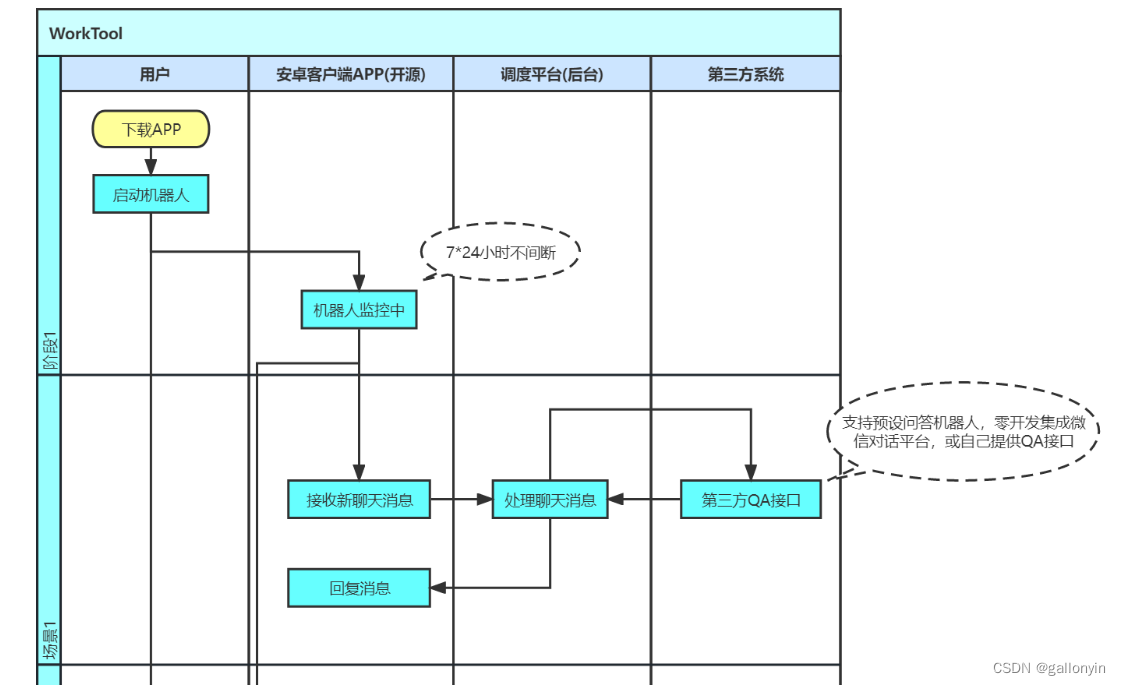
WorkTool企微机器人接入智能问答
一、前言 最新版的企微机器人已经集成 Chat ,无需开发可快速搭建智能对话机器人。 从官方介绍看目前集成版本使用模型为 3.5-turbo。 二、入门 创建 WorkTool 机器人 你可以通过这篇快速入门教程,来快速配置一个自己的企微机器人。 实现的流程如图&…...

C导入正则库问题
环境 操作系统:win11 专业版 gcc: gcc (x86_64-posix-seh-rev0, Built by MinGW-W64 project) 8.1.0 编辑器:vscode 要求 在c中使用正则表达式 遇到的问题以及解决思路 C标准中并没有正则表达式库 从其他地方下载正则表达式库即可。 http://gnuwin32.sourcefo…...
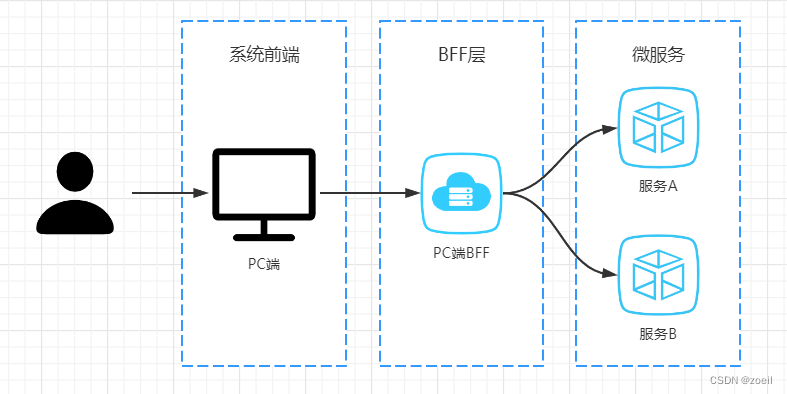
尚融宝05-Node.js入门
目录 一、Node.js的概念 1、JavaScript引擎 2、什么是Node.js 二、下载和安装 1、下载和安装 2、查看安装是否成功 三、初始Node.js程序 1、运行一个程序 常见问题 2、文件的读取 3、服务器端程序 三、Node.js的作用 1、Node.js的应用场景 2、BFF 解决什么问题 …...

「SAP ABAP」OPEN SQL(八)【WHERE语句大全】
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后端的开发语言A…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
