matlab仿真 模拟调制(下)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第五章内容,有兴趣的读者请阅读原书)



clear all
ts=0.001;
t=0:ts:10-ts;
fs=1/ts;
df=fs/length(t);
msg=randi([-3 3],100,1);
msg1=msg*ones(1,fs/10);
msg2=reshape(msg1.',1,length(t));
Pm=fft(msg2)/fs;
f=-fs/2:df:fs/2-df;
subplot(2,1,1)
plot(f,fftshift(abs(Pm)))
title('消息信号频谱')int_msg(1)=0;%消息信号积分(1)
for ii=1:length(t)-1int_msg(ii+1)=int_msg(ii)+msg2(ii)*ts;
endkf=50;
fc=250;%载波频率
Sfm=cos(2*pi*fc*t+2*pi*kf*int_msg);%(2)
Pfm=fft(Sfm)/fs;%FM信号频谱
subplot(2,1,2)
plot(f,fftshift(abs(Pfm)))%画出已调信号频谱
title('FM信号频谱')Pc=sum(abs(Sfm).^2)/length(Sfm)%已调信号功率
Ps=sum(abs(msg2).^2)/length(msg2)%消息信号功率fm=50;
betaf=kf*max(msg)/fm%调制指数
W=2*(betaf+1)*fm%调制信号带宽 代码中的注释(1)(2)为:
求调频指数的公式为:kf*Amax/fm,其中的Amax是振幅的最大值,这里可以理解为消息序列的最大绝对值


clear all
ts=0.001;
t=0:ts:5-ts;
fs=1/ts;
df=fs/length(t);
msg=randi([-3,3],10,1);
msg1=msg*ones(1,fs/2);
msg2=reshape(msg1.',1,length(t));
subplot(3,1,1)
plot(t,msg2)
title('消息信号')int_msg(1)=0;
for ii=1:length(t)-1int_msg(ii+1)=int_msg(ii)+msg2(ii)*ts;%调制信号中的对消息序列进行积分的部分
endkf=50;
fc=300;3
Sfm=cos(2*pi*fc*t+2*pi*kf*int_msg);%构建fm信号phase=angle(hilbert(Sfm).*exp(-j*2*pi*fc*t));%FM调制信号相位(1)
phi=unwrap(phase);%为了恢复相位,需要将相位卷绕解开
%unwrap函数的作用将相位信息进行平滑处理,使其在整个信号范围内保持连续性。dem=(1/(2*pi*kf)*diff(phi)/ts);%求相位微分,得到消息信号
dem(length(t))=0;
subplot(3,1,2)
plot(t,dem);
title('无噪声的解调信号')
y1=awgn(Sfm,20,'measured');%调制信号通过AWGN信道
y1(find(y1>1))=1;%调制信号限幅,限幅是为了减少寄生条幅的出现,提高信号的准确性
y1(find(y1<-1))=-1;
phase1=angle(hilbert(y1).*exp(-j*2*pi*fc*t));%信号解调
phi1=unwrap(phase1);
dem1=(1/(2*pi*kf)*diff(phi1)/ts);
dem1(length(t))=0;
subplot(3,1,3)
plot(t,dem1);
title('信噪比为20dB时的解调信号')(1):在求FM信号相位的过程中
因为复包络取相位就是信号的相位分量。

相关文章:

matlab仿真 模拟调制(下)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第五章内容,有兴趣的读者请阅读原书) clear all ts0.001; t0:ts:10-ts; fs1/ts; dffs/length(t); msgrandi([-3 3],100,1); msg1msg*ones(1,fs/10); msg2reshape(ms…...

RabbitMQ是什么?
RabbitMQ是一个开源的消息代理软件(Message Broker),它实现了高级消息队列协议(AMQP,Advanced Message Queuing Protocol),并支持多种消息传递协议。它最初由英国的Rabbit Technologies开发&…...

追问试面试系列:分布式id
hi 大家好,欢迎来到追问试面试系列:分布式id 面试中可能面试官不会直接问你分布式id问题,基本上都是因为你在某些面试题回答中提到了,所以就开始追问分布式id相关问题。 先看面试题 ● 面试官:什么是分布式id? ● 面试官:举个例子说说 ● 面试官:什么叫分库分表? ●…...

护网紧急情况应对指南:Linux 应急响应手册
继上一篇:护网紧急情况应对指南:Windows版v1.2全新升级版 之后 收到小伙伴后台要Linux应急手册,今天给大家安排上。 《Linux应急手册》是一本为Linux系统管理员和运维工程师量身打造的实用指南,旨在帮助他们快速应对各种突发状况…...

WEB攻防-通用漏洞-SQL 读写注入-MYSQLMSSQLPostgreSQL
什么是高权限注入 高权限注入指的是攻击者通过SQL注入漏洞,利用具有高级权限的数据库账户(如MYSQL的root用户、MSSQL的sa用户、PostgreSQL的dba用户)执行恶意SQL语句。这些高级权限账户能够访问和修改数据库中的所有数据,甚至执行…...
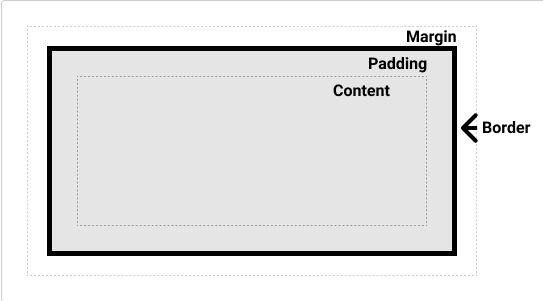
【前端学习笔记】CSS基础一
一、什么是CSS 1.CSS 介绍 CSS(Cascading Style Sheets,层叠样式表)是一种用来控制网页布局和设计外观的样式语言。它使得开发者可以分离网页的内容(HTML)和表现形式(样式),提高了…...
)
Github遇到的问题解决方法总结(持续更新...)
1.github每次push都需要输入用户名和token的解决方法 push前,执行下面命令 : git config --global credential.helper store 之后再输入一次用户名和token之后,就不用再输入了。 2.git push时遇到“fatal: unable to access https://githu…...

数字信封+数字签名工具类测试样例(Java实现)
加解密过程 加密: 生成加密方SM2密钥对用于签名使用生成的SM2私钥生成数字签名生成SM4对称密钥对明文进行对称加密使用与解密方提前约定好的SM2公钥对第三步中的SM4对称密钥进行非对称加密把【加密方SM2公钥】、【数字签名】、【SM4对称加密后的密文】和【SM2非对…...

The Schematic workflow failed. See above.
在使用 ng new 新建Angular项目的时候会报一个错误:The Schematic workflow failed. See above. 解决办法: 只需要在后面加上 --skip-install 参数,就不会报错了。 ng new myapp --skip-install...
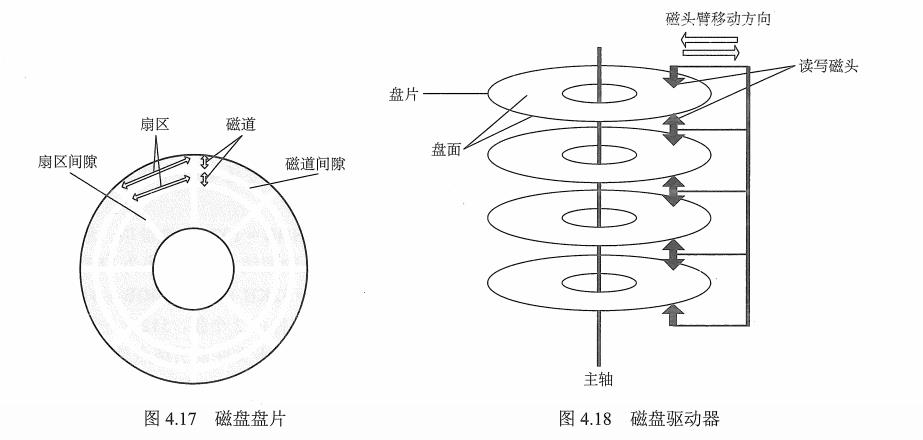
操作系统面试知识点总结4
#来自ウルトラマンメビウス(梦比优斯) 1 文件系统基础 1.1 文件的相关概念 文件是以计算机硬盘为载体的存储在计算机上的信息集合,可以是文本文档、图片、程序。 文件的结构:数据项、记录、文件(有结构文件、无结构式…...

Lua实现面向对象以及类的继承
0.简单前言 1、面向对象主要四个特征:封装,继承,多态,抽象 2、Lua是种简单精致小巧的语言,其本质是个表(table),变量和方法皆可看作为该表的元素。 P.S. 该博客和代码为个人编写习…...
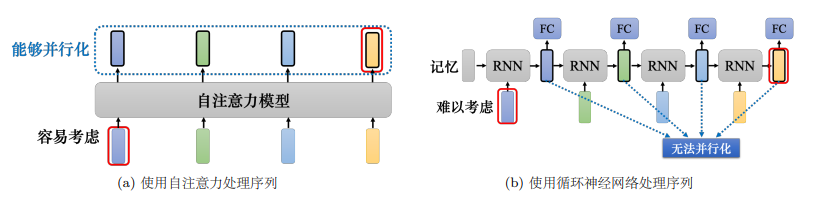
机器学习课程学习周报五
机器学习课程学习周报五 文章目录 机器学习课程学习周报五摘要Abstract一、机器学习部分1.1 向量序列作为模型输入1.1.1 文字的向量表达1.1.2 语音的向量表达 1.2 自注意力机制原理1.2.1 自注意力机制理论1.2.2 矩阵运算自注意力机制 1.3 多头自注意力1.4 位置编码1.5 截断自注…...

vue3.0学习笔记(二)——生命周期与响应式数据(ref,reactive,toRef,toRefs函数)
1. 组合API-setup函数 使用细节: setup 是一个新的组件选项,作为组件中使用组合API的起点。从组件生命周期来看,它的执行在组件实例创建之前vue2.x的beforeCreate执行。这就意味着在setup函数中 this 还不是组件实例,this 此时是…...

C++——QT:保姆级教程,从下载到安装到用QT写出第一个程序
登录官网,在官网选择合适的qt版本进行下载 这里选择5.12.9版本 点击exe文件下载,因为服务器在国外,国内不支持,所以可以从我的网盘下载 链接: https://pan.baidu.com/s/1XMILFS1uHTenH3mH_VlPLw 提取码: 1567 --来自百度网盘超级…...
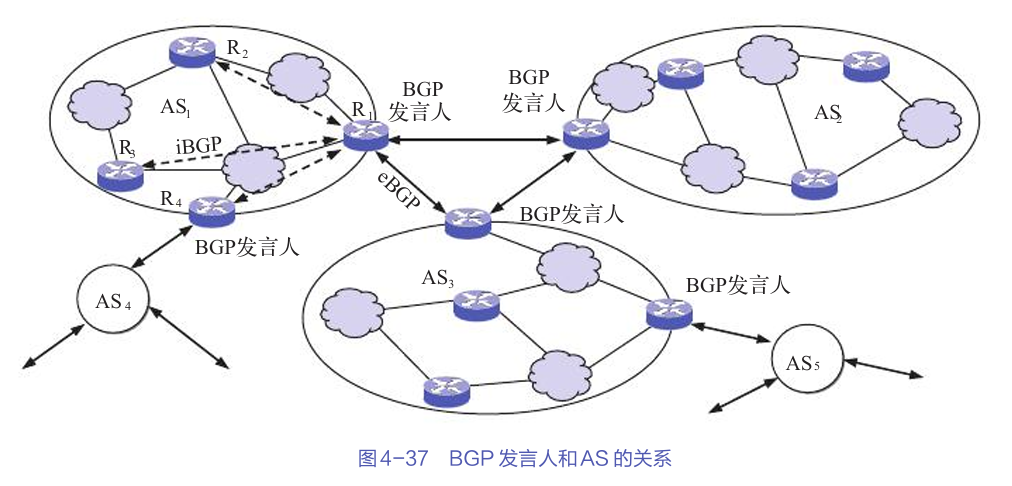
掌握互联网路由选择协议:从基础入门到实战
文章目录 路由选择协议的基本概念路由选择算法的分类分层次的路由选择协议路由信息协议(RIP)内部网关协议:OSPF外部网关协议:BGP互联网中的实际应用总结 互联网的路由选择协议是网络通信的核心,它决定了数据包如何在网…...

[笔记]ONVIF服务端实现[进行中...]
1.文档搜索: 从:https://www.cnblogs.com/liwen01/p/17337916.html 跳转到了:ONVIF协议网络摄像机(IPC)客户端程序开发(1):专栏开篇_onvif 许振坪-CSDN博客 1.1原生代码支持&…...

深度强化学习 ②(DRL)
参考视频:📺王树森教授深度强化学习 前言: 最近在学习深度强化学习,学的一知半解😢😢😢,这是我的笔记,欢迎和我一起学习交流~ 这篇博客目前还相对比较乱,后面…...
)
线性代数重要知识点和理论(下)
奇异值分解 奇异值分解非常重要且有趣。首先对于 n n n\times n nn对称矩阵 A A A,可以通过对角化得到其对角化形式 A P D P − 1 APDP^{-1} APDP−1,但是如果 A A A不是对称矩阵或者不是方阵,则不能进行对角化,但是可以通过奇…...

独立开发者系列(35)——python环境的理解
新手阶段,为了快速入门,基本都是直接开始写python代码实现自己想要的效果,类似搭建博客,写个web服务器,搭建简易聊天室,偶尔也写些爬虫,或者使用pygame写个简单小游戏,也有tk库做点简…...

中小企业常见的网络安全问题及防范措施
在数字化浪潮的推动下,我国中小企业的信息化建设取得了显著成就。然而,随着网络安全形势的日益严峻,中小企业在网络安全方面的短板逐渐暴露出来。本文将从中小企业网络安全现状出发,深入剖析其存在的问题,并提出针对性…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
