【学习笔记】子集DP
背景
有一类问题和子集有关。
给你一个集合 S S S,令 T T T 为 S S S 的超集,也就是 S S S 所有子集的集合,求 T T T 中所有元素的和。
暴力1
先预处理子集的元素和 A i A_i Ai,再枚举子集。
for(int s=0; s<(1<<n); s++)for(int i=0; i<(1<<n); i++)if(s&i) f[s]+=A[i];
时间复杂度 O ( n 4 ) O(n^4) O(n4)
暴力2
其实枚举子集有个小 trick
for(int s=0; s<(1<<n); s++)for(int i=s; i>0; i=(i-1)&s)f[s]+=A[i];
由二项式定理,时间复杂度为 O ( 3 n ) O(3^n) O(3n)
子集DP
令 g s , i g_{s,i} gs,i 为状态为 s s s,只考虑后 i i i 位转移的答案。
那么转移就是
g s , i = { g s , i − 1 s & ( 1 < < i ) = 0 g s , i − 1 + g s ⨁ ( 1 < < i ) , i − 1 o t h e r w i s e g_{s,i} = \begin{cases} g_{s,i-1} & s\&(1<<i)=0 \\g_{s,i-1} +g_{s\bigoplus(1<<i),i-1}&otherwise\end{cases} gs,i={gs,i−1gs,i−1+gs⨁(1<<i),i−1s&(1<<i)=0otherwise
这样可以做到不重不漏的转移。
推荐一篇blog,非常形象:https://www.cnblogs.com/maple276/p/17975253
可以发现,这个转移只和上一层有关,所以第二维是可以省略的。
前缀和(子集向超集转移)
for(int i=0; i<n; i++)
{for(int s=0; s<(1<<n); s++){if(s&_2)(f[s]+=f[s^_2])%(mod-1);}_2<<=1;
}
后缀和(超集向子集转移)
for(int i=0; i<n; i++)
{for(int s=0; s<(1<<n); s++){if(!(s&_2))(f[s]+=f[s^_2])%(mod-1);}_2<<=1;
}
差分
//后缀差分
for(int i=0; i<20; i++)
{for(int s=0; s<S; s++){if(!(s&_2))(f[s]-=f[s^_2])%=mod;}_2<<=1;
}
例题
CF165E
定义 x x x 和 y y y 相容为 x & y = 0 x\&y=0 x&y=0,给你一个序列 A A A,对于每个元素,在 A A A 中找到和它相容的元素。 ∣ A ∣ ≤ 1 0 6 , A i ≤ 4 × 1 0 6 |A|\leq 10^6,A_i\leq 4\times 10^6 ∣A∣≤106,Ai≤4×106
思路
x & y = 0 x\&y=0 x&y=0 等价于 x ˜ & y = y \~x\&y=y x˜&y=y,那么只需要对 A A A做类似前缀和的操作,加法改成覆盖即可。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int S=1<<22;
void O_o()
{int n;cin>>n;vector<int> f(S,-1),a(n+1);for(int i=1; i<=n; i++){cin>>a[i];f[a[i]]=a[i];}int _2=1;for(int i=0; i<=21; i++){for(int s=0; s<S; s++){if(!(s&_2)) continue;if(f[s^_2]!=-1)f[s]=f[s^_2];}_2<<=1;}int t=S-1;for(int i=1; i<=n; i++){cout<<f[t^a[i]]<<" ";}cout<<"\n";
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout<<fixed<<setprecision(2);int T=1;
// cin>>T;while(T--){O_o();}
}相关文章:

【学习笔记】子集DP
背景 有一类问题和子集有关。 给你一个集合 S S S,令 T T T 为 S S S 的超集,也就是 S S S 所有子集的集合,求 T T T 中所有元素的和。 暴力1 先预处理子集的元素和 A i A_i Ai,再枚举子集。 for(int s0; s<(1<…...

苦学Opencv的第十四天:人脸检测和人脸识别
Python OpenCV入门到精通学习日记:人脸检测和人脸识别 前言 经过了十三天的不懈努力,我们终于也是来到了人脸检测和人脸识别啦!相信大家也很激动吧。接下来我们开始吧! 人脸识别是基于人的脸部特征信息进行身份识别的一种生物识…...

PyTorch学习(1)
PyTorch学习(1) CIFAR-10数据集-图像分类 数据集来源是官方提供的: torchvision.datasets.CIFAR10()共有十类物品,需要用CNN实现图像分类问题。 代码如下:(CIFAR_10_Classifier_Self_1.py) import torch import t…...

三思而后行:计算机行业的决策智慧
在计算机行业,"三思而后行"这一原则显得尤为重要。在这个快速发展、技术不断更新换代的领域,每一个决策都可能对项目的成功与否产生深远的影响。以下是一篇关于在计算机行业中三思重要性的文章。 三思而后行:计算机行业的决策智慧 …...

Linux--Socket编程UDP
前文:Socket套接字编程 UDP协议特点 无连接:UDP在发送数据之前不需要建立连接,减少了开销和发送数据之前的时延。尽最大努力交付:UDP不保证可靠交付,主机不需要维持复杂的连接状态表。面向报文:UDP对应用层…...

《javaEE篇》--单例模式详解
目录 单例模式 饿汉模式 懒汉模式 懒汉模式(优化) 指令重排序 总结 单例模式 单例模式属于一种设计模式,设计模式就好比是一种固定代码套路类似于棋谱,是由前人总结并且记录下来我们可以直接使用的代码设计思路。 单例模式就是,在有…...

Java核心 - Lambda表达式详解与应用示例
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有疑问和建议,请私信或评论留言! 前言 Lambda表达式是…...

算法通关:006_1二分查找
二分查找 查找一个数组里面是否存在num主要代码运行结果 详细写法自动生成数组和num,利用对数器查看二分代码是否正确 查找一个数组里面是否存在num 主要代码 /*** Author: ggdpzhk* CreateTime: 2024-07-27*/ public class cg {//二分查找public static boolean …...

总结一些vue3小知识3
总结一些vue3小知识1:http://t.csdnimg.cn/C5vER 总结一些vue3小知识2:http://t.csdnimg.cn/sscid 1.限制时间选择器只能选择后面的日期 说明:disabled-date属性是一个用来判断该日期是否被禁用的函数,接受一个 Date 对象作为参…...

JAVAWeb实战(前端篇)
项目实战一 0.项目结构 1.创建vue3项目,并导入所需的依赖 npm install vue-router npm install axios npm install pinia npm install vue 2.定义路由,axios,pinia相关的对象 文件(.js) 2.1路由(.js) import {cre…...

axios请求大全
本文讲解axios封装方式以及针对各种后台接口的请求方式 axios的介绍和基础配置可以看这个文档: 起步 | Axios中文文档 | Axios中文网 axios的封装 axios封装的重点有三个,一是设置全局config,比如请求的基础路径,超时时间等,第二点是在每次…...

C# 简单的单元测试
文章目录 前言参考文档新建控制台项目新建测试项目添加引用添加测试方法测试结果(有错误)测试结果,通过正规的方法抛出异常 总结 前言 听说复杂的项目最好都要单元测试一下。我这里也试试单元测试这个功能。到时候调试起来也方便。 参考文档 C# 单元测试…...

Linux中Mysql5.7主从架构(一主多从)配置教程
🏡作者主页:点击! 🐧Linux基础知识(初学):点击! 🐧Linux高级管理防护和群集专栏:点击! 🔐Linux中firewalld防火墙:点击! ⏰️创作…...
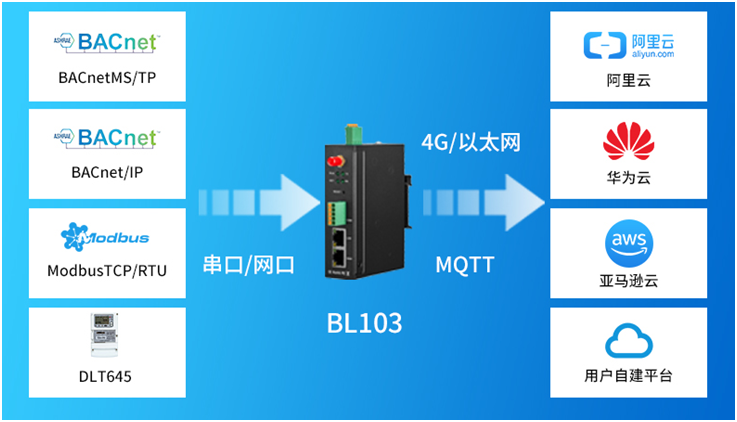
BACnet物联网关BL103:Modbus协议转BACnet/MSTP
随着物联网技术在楼宇自动化与暖通控制系统中的迅猛发展,构建一种既经济高效又高度可靠的协议转换物联网关成为了不可或缺的核心硬件组件。在此背景下,我们钡铼特别推荐一款主流的BAS(楼宇自动化系统)与BACnet物联网关——BL103&a…...

Go 语言条件变量 Cond
1.Cond 的使用方法 Go 标准库提供 Cond 同步原语的目的是为等待/通知场景下的并发操作提供支持。Cond 通常用于等待某个条件的一组 goroutine,当条件变为 true 时,其中一个或者所有的 goroutine 会被唤醒执行。 Cond 与某个条件相关,这个条件需要一组 goroutine 协作达到。当这…...

PostgreSQL 中如何重置序列值:将自增 ID 设定为特定值开始
我是从excel中将数据导入,然后再通过sql插入数据,就报错。 需要设置自增ID开始值 1、确定序列名称: 首先,需要找到与的增字段相关的序列名称。假设表名是 my_table 和自增字段是 id,可以使用以下查询来获取序列名称…...

Unity 之 【Android Unity 共享纹理】之 Android 共享图片给 Unity 显示
Unity 之 【Android Unity 共享纹理】之 Android 共享图片给 Unity 显示 目录 Unity 之 【Android Unity 共享纹理】之 Android 共享图片给 Unity 显示 一、简单介绍 二、共享纹理 1、共享纹理的原理 2、共享纹理涉及到的关键知识点 3、什么可以实现共享 不能实现共享…...

Go语言的数据结构
数据结构 数组 支持多维数组,属于值类型,支持range遍历 例子:随机生成长度为10整数数组 package main import ("fmt""math/rand" ) // 赋值 随机获取100以内的整数 func RandomArrays() {var array [10]int //声明var…...

python_在sqlite中创建表并写入表头
python_在sqlite中创建表并写入表头 import sqlite3def write_title_to_sqlite(tableName,titleList,dataTypeGroupsList,database_path):conn sqlite3.connect(database_path)# 创建游标cursor conn.cursor()#MEMO 长文本#create_table_bodycreate_table_body "序号 …...

1.c#(winform)编程环境安装
目录 安装vs创建应用帮助查看器安装与使用( msdn) 安装vs 安装什么版本看个人心情,或者公司开发需求需要 而本栏全程使用vs2022进行开发c#,着重讲解winform桌面应用开发 使用***.net framework***开发 那先去官网安装企业版的vs…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
