自动控制:带死区的PID控制算法
带死区的PID控制算法
在计算机控制系统中,为了避免控制动作过于频繁,消除因频繁动作所引起的振荡,可采用带死区的PID控制。带死区的PID控制通过引入一个死区,使得在误差较小的范围内不进行控制动作,从而减少控制系统的频繁调整,提高系统的稳定性。
理论基础
传统PID控制算法
传统PID控制器的控制律为:
u ( t ) = K p e ( t ) + K i ∫ e ( t ) d t + K d d e ( t ) d t u(t) = K_p e(t) + K_i \int e(t) \, dt + K_d \frac{d e(t)}{dt} u(t)=Kpe(t)+Ki∫e(t)dt+Kddtde(t)
其中:
- u ( t ) u(t) u(t) 是控制输入
- e ( t ) = r ( t ) − y ( t ) e(t) = r(t) - y(t) e(t)=r(t)−y(t) 是误差信号
- K p K_p Kp 是比例增益
- K i K_i Ki 是积分增益
- K d K_d Kd 是微分增益
带死区的PID控制算法
带死区的PID控制器通过在误差信号上引入一个死区 δ \delta δ,使得在误差 e ( t ) e(t) e(t) 的绝对值小于死区 δ \delta δ 时,控制输入 u ( t ) u(t) u(t) 不进行调整。其控制律为:
u ( t ) = { K p e ( t ) + K i ∫ e ( t ) d t + K d d e ( t ) d t if ∣ e ( t ) ∣ > δ 0 if ∣ e ( t ) ∣ ≤ δ u(t) = \begin{cases} K_p e(t) + K_i \int e(t) \, dt + K_d \frac{d e(t)}{dt} & \text{if } |e(t)| > \delta \\ 0 & \text{if } |e(t)| \leq \delta \end{cases} u(t)={Kpe(t)+Ki∫e(t)dt+Kddtde(t)0if ∣e(t)∣>δif ∣e(t)∣≤δ
其中:
- δ \delta δ 是死区的阈值
公式推导
带死区的PID控制算法可以通过以下步骤推导得到:
- 定义误差信号:
e ( t ) = r ( t ) − y ( t ) e(t) = r(t) - y(t) e(t)=r(t)−y(t)
- 判断误差是否在死区范围内:
∣ e ( t ) ∣ ≤ δ |e(t)| \leq \delta ∣e(t)∣≤δ
- 根据误差范围计算控制输入:
u ( t ) = { K p e ( t ) + K i ∫ e ( t ) d t + K d d e ( t ) d t if ∣ e ( t ) ∣ > δ 0 if ∣ e ( t ) ∣ ≤ δ u(t) = \begin{cases} K_p e(t) + K_i \int e(t) \, dt + K_d \frac{d e(t)}{dt} & \text{if } |e(t)| > \delta \\ 0 & \text{if } |e(t)| \leq \delta \end{cases} u(t)={Kpe(t)+Ki∫e(t)dt+Kddtde(t)0if ∣e(t)∣>δif ∣e(t)∣≤δ
Python代码示例
下面是一个实现带死区的PID控制器的Python代码示例。假设我们有一个简单的温度控制系统,通过带死区的PID控制器保持系统温度在期望值。
import numpy as np
import matplotlib.pyplot as plt# 定义系统参数
dt = 0.1 # 时间步长
t = np.arange(0, 20, dt) # 时间数组
n = len(t)# 初始化状态变量
temperature = np.zeros(n) # 系统温度
desired_temperature = np.zeros(n) # 期望温度
desired_temperature[100:] = 50 # 期望温度从时间t=10s开始为50
external_disturbance = np.sin(t) * 5 # 外界扰动# 控制器参数
Kp = 2.0 # 比例增益
Ki = 1.0 # 积分增益
Kd = 0.5 # 微分增益
delta = 1.0 # 死区阈值# 初始化误差变量
e_prev = 0 # 上一时刻的误差
integral = 0 # 误差积分# 模拟系统
for i in range(1, n):# 计算误差e = desired_temperature[i] - temperature[i-1]# 判断误差是否在死区范围内if abs(e) > delta:# 误差积分integral += e * dt# 误差微分derivative = (e - e_prev) / dt# PID控制器u = Kp * e + Ki * integral + Kd * derivativeelse:u = 0 # 在死区范围内,控制输入为0# 更新系统温度temperature[i] = temperature[i-1] + (u + external_disturbance[i]) * dt# 更新上一时刻的误差e_prev = e# 绘制结果
plt.figure(figsize=(10, 4))
plt.plot(t, desired_temperature, label='Desired Temperature')
plt.plot(t, temperature, label='Actual Temperature')
plt.plot(t, external_disturbance, label='External Disturbance')
plt.xlabel('Time [s]')
plt.ylabel('Temperature')
plt.legend()
plt.title('Dead Zone PID Control for Temperature System')
plt.grid(True)
plt.show()

代码解释
- 系统参数和时间数组:定义了时间步长
dt和时间数组t,用来模拟系统在一段时间内的行为。 - 状态变量初始化:初始化了系统温度
temperature、期望温度desired_temperature和外界扰动external_disturbance。 - 控制器参数:定义了带死区的PID控制器的比例增益
Kp、积分增益Ki、微分增益Kd和死区阈值delta。 - 误差变量初始化:初始化了上一时刻的误差
e_prev和误差积分integral。 - 系统模拟:通过迭代计算,在每个时间步长内根据带死区的PID控制律计算控制输入,并更新系统温度。
- 结果绘制:使用
matplotlib绘制系统温度、期望温度和外界扰动的变化曲线。
结论
带死区的PID控制器通过在误差信号上引入一个死区,有效减少了控制系统的频繁调整,避免了因频繁动作所引起的系统振荡,从而提高了系统的稳定性。在实际应用中,带死区的PID控制器适用于控制量需要频繁调整的场合,能够显著改善系统的动态特性。结合Python代码示例,可以更直观地理解带死区的PID控制器的基本原理和实现方法。
相关文章:

自动控制:带死区的PID控制算法
带死区的PID控制算法 在计算机控制系统中,为了避免控制动作过于频繁,消除因频繁动作所引起的振荡,可采用带死区的PID控制。带死区的PID控制通过引入一个死区,使得在误差较小的范围内不进行控制动作,从而减少控制系统的…...

橙单后端项目下载编译遇到的问题与解决
今天下载orange-admin项目,不过下载下来运行出现一些问题。 1、涉及到XMLStreamException的几个类都出现下面的错误 The package javax.xml.stream is accessible from more than one module: <unnamed>, java.xml ctrl-shift-t 可以找到这个引入是哪些包里…...

EasyExcel 初使用—— Java 实现多种写入 Excel 功能
前言 大家好,我是雪荷。之前有一篇博客(EasyExcel 初使用—— Java 实现读取 Excel 功能_java easyexcel.read-CSDN博客)介绍了 Java 如何读取 Excel 表格,那么此篇博客就和大家介绍下 Java 如何利用 EasyExcel 写入 Excel。 Ea…...

MySQL 和 SQL Server 中的连表更新 UPDATE JOIN 写法比较
MySQL 和 SQL Server 中的连表更新 UPDATE JOIN 写法比较 一、前言1. MySQL 写法1.1 解释 2. SQL Server 写法2.1 解释 二、总结 一、前言 在关系型数据库管理系统(RDBMS)中,使用 UPDATE 语句进行表格更新是非常常见的操作。特别是当需要根据…...

手把手教你FL Studio 24.1.1.4234中文破解安装激活图文激活教程
在数字化音乐制作的浪潮中,FL Studio 24.1.1.4234中文破解版的发布无疑又掀起了一股新的热潮。这款由Image-Line公司开发的数字音频工作站(DAW)软件,以其强大的功能和易用的界面,赢得了全球无数音乐制作人的青睐。本文…...

使用Spring Boot与Spire.Doc实现Word文档的多样化操作
博客主页: 南来_北往 系列专栏:Spring Boot实战 前言 使用Spring Boot与Spire.Doc实现Word文档的多样化操作具有以下优势: 强大的功能组合:Spring Boot提供了快速构建独立和生产级的Spring应用程序的能力,而Spire.Doc则…...

从食堂采购系统源码到成品:打造供应链采购管理平台实战详解
本篇文章,笔者将详细介绍如何从食堂采购系统的源码开始,逐步打造一个完备的供应链采购管理平台,帮助企业实现采购流程的智能化和高效化。 一、需求分析与规划 一般来说,食堂采购系统需要具备以下基本功能: 1.供应商…...

在window将Redis注册为服务
将redis注册为系统服务,开启自启动 安装服务 默认注册完之后会自动启动,在window中的服务看一下,如果启动类型为自动,状态是自动运行则启动完成。如果是手动,需要右键属性调整为自动,在点击启动,…...

PHP商城案例
http://www.e9933.com/...

Linux:bash在被调用时会读取哪些启动文件?
(本文基于5.1-6ubuntu1.1版本的bash) bash在被调用时会读取哪些启动文件?要回答这个问题,首先要弄清楚两个概念:login shell和interactive shell。 login shell login shell是指这样的shell: 第一个命令行参数(进程…...

帆软FineReport之替换函数
在日常帆软FineReport中经常会使用字符串替换函数,记录下来,方便备查。 一、字符串替换 第一种、指定文本替换 使用SUBSTITUTE函数,语法如下所示 SUBSTITUTE(text,old_text,new_text,instance_num) 字段…...

Redis的应用场景及类型
目录 一、Redis的应用场景 1、限流 2、分布式锁 3、点赞 4、消息队列 二、Redis类型的命令及用法 1、String类型 2、Hash类型 3、List类型 4、Set类型 5、Zset类型 6、Redis工具类 Redis使用缓存的目的就是提升读写性能 实际业务场景下,我们就可以把 Mys…...

【图像处理】不智能的目标识别
目录 目标识别的划分 识别入门 概念学习 滤波 模版 阈值化 形态学操作 开运算 闭运算 编程语言 示例 大家有没有想过在没有人工智能或者说没有机器学习的的时候,计算机是怎么做目标识别的? 计算机视觉时至今日也是急需人才的领域&…...

《500 Lines or Less》(5)异步爬虫
https://aosabook.org/en/500L/a-web-crawler-with-asyncio-coroutines.html ——A. Jesse Jiryu Davis and Guido van Rossum 介绍 网络程序消耗的不是计算资源,而是打开许多缓慢的连接,解决此问题的现代方法是异步IO。 本章介绍一个简单的网络爬虫&a…...

Transformer!自注意力机制的高层级理解Attention Is All You Need!
背景 最近在不断深入学习LLM的相关内容,那么transformer就是一个绕不开的话题。然而对于一个NLP门外汉来说,论文看得是真头疼,总览全网,我们似乎缺少一个至高而下的高层级理解。所以本文就来弥补此方面的缺失~ 本文并不讲解有关…...

关于使用Postman在请求https网址没有响应,但是用浏览器有响应的问题解决
一、问题描述 使用postman调用正式环境的公共接口,无需鉴权,但是产生了返回状态码200,但是data中却无数据,如下 {"code": "200","message": "操作成功","data": {"qr_c…...

【React 】开发环境搭建详细指南
文章目录 一、准备工作1. 安装 Node.js 和 npm2. 选择代码编辑器 二、创建 React 项目1. 使用 Create React App2. 手动配置 React 项目 三、集成开发工具1. ESLint 和 Prettier2. 使用 Git 进行版本控制 在现代前端开发中,React 是一个非常流行的框架,用…...
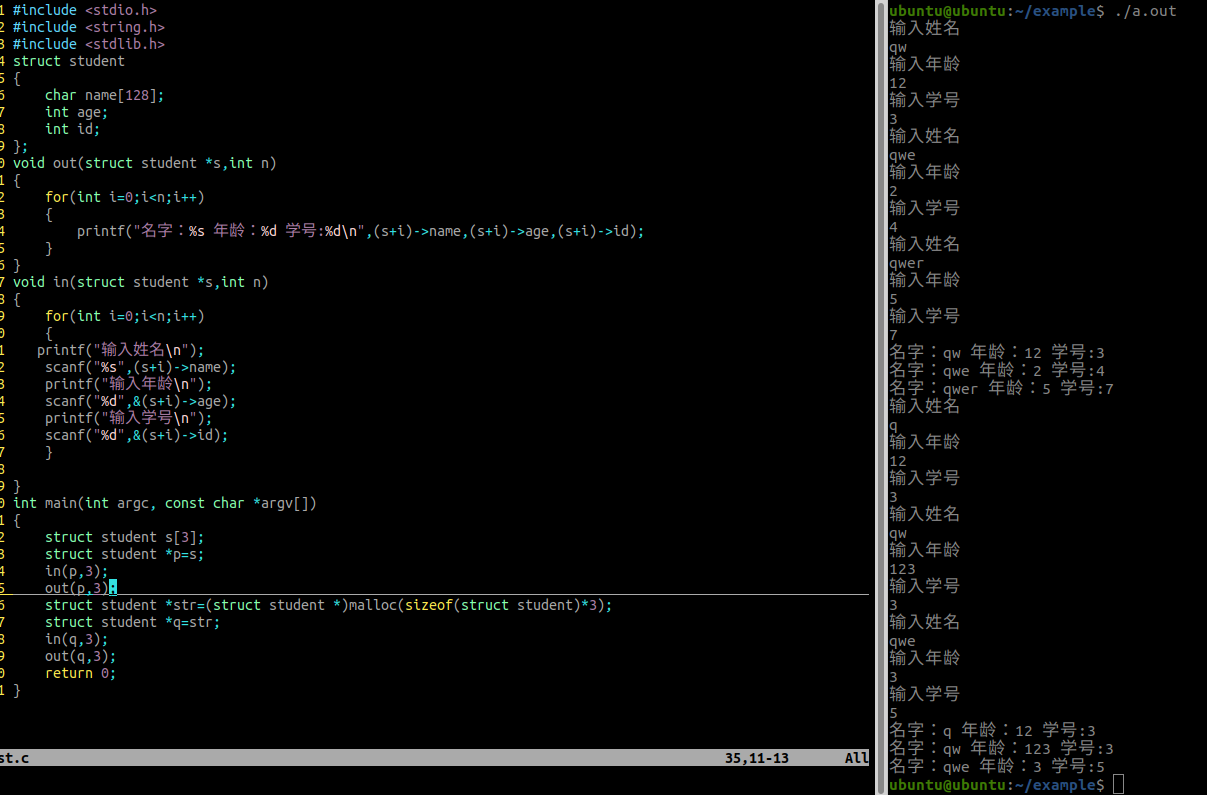
结构体笔记
结构体 C语言中的数据类型: 基本数据类型:char/int/short/double/float/long 构造数据类型:数组,指针,结构体,共用体,枚举 概念: 结构体是用户自定义的一种数据类型,…...

Elasticsearch:Golang ECS 日志记录 - zerolog
ECS 记录器是你最喜欢的日志库的格式化程序/编码器插件。它们可让你轻松地将日志格式化为与 ECS 兼容的 JSON。在本教程中,我将详述如何 编码器以 JSON 格式记录日志,并以 ECS 错误格式处理错误字段的记录。 默认情况下,会添加以下字段&…...

Ip2region - 基于xdb离线库的Java IP查询工具提供给脚本调用
文章目录 Pre效果实现git clone编译测试程序将ip2region.xdb放到指定目录使用改进最终效果 Pre OpenSource - Ip2region 离线IP地址定位库和IP定位数据管理框架 Ip2region - xdb java 查询客户端实现 效果 最终效果 实现 git clone git clone https://github.com/lionsou…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
