详解线段树 ---更新查询
目录
一.问题引入
二.线段树
1.什么是线段树
2.线段树的举例
三.构建线段树
1.思路分析
2.代码实现
四.更新
1.思路分析
2.代码实现
五.查询
1.思路分析
2.代码实现
一.问题引入
有n个整数的数组,我们要 求解下标从left到right的元素之和为多少(query操作),然后还需要更新下标为index的值改为val(update操作),这个时候的时间复杂度为多少.
方法一:对于第一个问题(query)直接相加,这样的时间复杂度为O(n),第二个问题(update)的时间复杂度为O(1)
方法二:如果我们需要多次的query操作,我们是否有方法可以将降低时间复杂度?这个时候最好的办法就是把这n个整数的前缀和数组求解出来,每一次只需要prefix[right]-prefix[left-1]即可求解出来答案,这样的时间复杂度就降到了O(1),但是这个时候update操作的时间复杂度就升到了O(n),因为我们需要对前缀和数组index之后都进行修改.具体可以参考这篇博客看前缀和相关的内容:Java之前缀和算法_java前缀和算法_允歆辰丶的博客-CSDN博客
因此当我们采用无论哪一种方法,对于一种操作的时间复杂度可能很低,但是对另外一种操作的时间复杂度是很高的,因此是否可以有一种方法,可能将两种操作的时间复杂度平均一下,当然有,就是我们接下来要介绍的线段树,对于两种操作的时间复杂度都为O(log n);
二.线段树
1.什么是线段树
线段树是一种经典的数据结构,用于处理区间查询问题,例如区间求和、区间最小值、区间最大值等。它的基本思想是将区间递归地划分为若干个子区间,并将每个子区间的信息保存在一个节点中,从而形成一棵树形结构,即线段树。
线段树的每个节点都代表一个区间,如果该节点表示的区间与待查询的区间有交集,那么该节点保存的信息就可能对查询有用。因此,在查询时,只需要访问与待查询区间相交的节点即可,而不需要访问整棵树。
线段树通常使用数组来实现,其空间复杂度为 O(n),其中n是区间的长度。线段树的建树复杂度为 O(n),单次查询复杂度为 O(\log n)。
2.线段树的举例
我们对数组arr(如下图)构建一颗线段树(如下下图),此时叶子结点就是数组下标为index的值,他们的根结点为叶子结点的之和,一层层向上,根结点为整个数组的和36(也就是index为0到5的和)
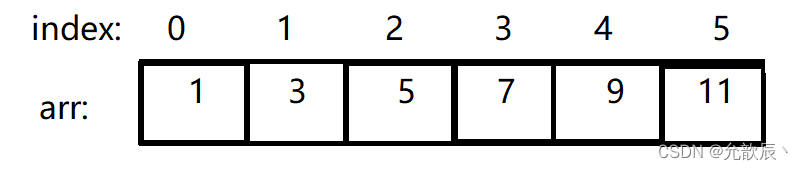

三.构建线段树
1.思路分析
构建一颗线段树可以用数组来模拟树的实现,知道根结点下标(也就是tree数组的node),这个时候它的左子节点为:node_left = node * 2 + 1;右子节点为:node_right = node * 2 + 2;node左节点的对应arr数组的下标范围为[start,mid],node右节点的对应arr数组的下标范围为[mid,end],这个时候我们进行递归创建这个tree数组,我们可以知道递归要到叶子结点,对叶子结点的下标进行赋值,然后再一步步回溯向上对上一层的父节点进行赋值,最后完成对根结点的赋值,所以我们递归的出口为递归到叶子结点,也就是start==end,这个时候赋值 tree[node] = arr[start];
2.代码实现
public static void buildTree(int[] arr, int[] tree, int node, int start, int end) {if (start == end) {tree[node] = arr[start];return;}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;buildTree(arr, tree, node_left, start, mid);buildTree(arr, tree, node_right, mid + 1, end);tree[node] = tree[node_left] + tree[node_right];}四.更新
1.思路分析
当我们需要对arr数组中的下标为index的元素进行数值的修改,这个时候也需要对线段树进行更新,例如将下标为3的数值修改为6,这个时候需要递归到下标范围为3的tree数组的下标,然后对值进行修改,然后一层层向上回溯对这半区的树值全部进行修改,我们只需要加上一个范围的判断,选择往左子树递归还是向右子树递归即可

2.代码实现
public static void updateTree(int[] arr, int[] tree, int node, int start, int end, int index, int val) {if (start == end) {arr[index] = val;tree[node] = val;return;}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;if (index >= start && index <= mid) {updateTree(arr, tree, node * 2 + 1, start, mid, index, val);} else {updateTree(arr, tree, node * 2 + 2, mid + 1, end, index, val);}tree[node] = tree[node_left] + tree[node_right];}五.查询
1.思路分析
查询代码实现起来是有一定的复杂,首先我们可以先判断返回值为0的情况,也就是需要求和的范围不在当前树的根结点所在的范围内的,一共有两种情况:一种当start>right,一种当left>end,这个时候直接返回0.

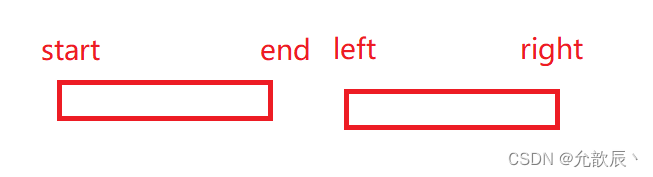
还有当出现如下图的情况时,直接返回当前结点的值,没必要继续向下递归,因为此时范围全部都符合了

这个时候最后我们需要把左边的符合范围的和 加上 右边符合范围的和 ,最终的结果就是我们需要求解的范围.
2.代码实现
/*** * @param arr 原数组* @param tree 构建的tree数组* @param node 根结点在tree数组的下标* @param start 原数组从start索引开始* @param end 原数组到end索引结束* @param left 求和从left索引开始* @param right 到right索引结束的和* @return*/public static int queryTree(int[] arr, int[] tree, int node, int start, int end, int left, int right) {if (right < start || end < left) {return 0;} else if (left <= start && right >= end) {return tree[node];}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;int sum_left = queryTree(arr, tree, node_left, start, mid, left, right);int sum_right = queryTree(arr, tree, node_right, mid + 1, end, left, right);return sum_left + sum_right;}
相关文章:

详解线段树 ---更新查询
目录 一.问题引入 二.线段树 1.什么是线段树 2.线段树的举例 三.构建线段树 1.思路分析 2.代码实现 四.更新 1.思路分析 2.代码实现 五.查询 1.思路分析 2.代码实现 一.问题引入 有n个整数的数组,我们要 求解下标从left到right的元素之和为多少(query操作),然后还…...

【C语言进阶:刨根究底字符串函数】strncpy、strncat、strncmp函数
再前几篇的博客中大家可能发现了,strcpy,strcat,strcmp 这三个函数在使用时对源字符串没有长度限制,几乎是将源字符串的内容全部进行操作。在VS编译器中的这些函数显得不安全了,因此VS会提醒你在其后加上 _s &#x…...

计算机面试常见问答题目
英语口语 自我介绍 Hello, teachers. My name is Wang Xu. I come from Ningxia. I graduated from the School of Computer Science, Xi an Jiaotong University, majoring in Internet of Things. Next, I will introduce myself from four aspects. First of all, I studi…...
mac pro m1:安装dump文件内存分析工具——MAT
0. 引言 本文主要针对mac m1下安装Jprofiler进行讲解,安装核心步骤同样适用于其他系统 1. 安装 如果使用的是eclipse可以在插件中直接安装MAT,因为我使用的是idea开发,所以选择独立安装MAT工具 1、下载地址:https://www.eclip…...
并发基础之线程池(Thread Pool)
目录前言何为线程池线程池优势创建线程池方式直接实例化ThreadPoolExecutor类JUC Executors 创建线程池线程池挖掘Executors简单介绍ThreadPoolExecutor核心类ThreadPoolExecutor 类构造参数含义线程池运行规则线程设置数量结语前言 相信大家都知道当前的很多系统架构都要求高…...
【C语言进阶】内存函数
天生我材必有用,千金散尽还复来。 ——李白 目录 前言 一.memcpy函数 1.实现memcpy函数 2.模拟实现memcpy函数 二.memmove函数 1.实现memmove函数 2.模拟实现memmove函数 三.memcpy函数和memmove函数的关系 四.memcm…...
Java开发 - ELK初体验
前言 前面我们讲过消息队列,曾提到消息队列也具有保存消息日志的能力,今天要说的EL看也具备这个能力,不过还是要区分一下功能的。消息队列的日志主要指的是Redis的AOF,实际上只是可以利用了消息队列来保存,却并不是消…...

AI_Papers周刊:第六期
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 2023.03.13—2023.03.19 文摘词云 Top Papers Subjects: cs.CL 1.UPRISE: Universal Prompt Retrieval for Improving Zero-Shot Evaluation 标题:UPRISE:改进零样本评估…...

JS运行环境、包管理、打包工具总结
🌳JS运行环境-node.js 运行环境就是代码解析和执行的程序,比如jvm等虚拟机,他们的主要工作就是根据设定的语法规则解析编译代码,然后运行代码。 js的语法规则遵循ES规范。 🍁node.js Node.Js官网 Node.js是一种基于Ch…...

day4网络编程(广播和组播)
1.广播 发送端(类似于客户端) 流程: 创建套接字 填充接收端(服务器)网络信息结构体 bind(非必须绑定) 设置允许广播 向接收端(服务器)发送数据 关闭套接字文件 #include <stdio.h> #in…...

Vue3 自动引入组件及函数、动态生成侧边栏路由
Vue3 自动引入组件及函数、动态生成侧边栏路由 1、安装依赖 npm install -D unplugin-auto-import unplugin-icons unplugin-vue-components插件使用说明 unplugin-auto-import 说明 —— 自动引入函数、组件 unplugin-vue-components 说明 —— 自动注册组件 unplugin-ic…...

人工智能交互系统界面设计
文章目录前言一、项目介绍二、项目准备三、项目实施1.导入相关库文件2.人脸信息验证功能3.语音交互与TCP数据通信4.数据信息可视化四、相关附件前言 在现代信息化时代,图形化用户界面(Graphical User Interface, GUI)已经成为各种软件应用和…...
蓝桥杯嵌入式第一课--创建工程
概述学习本节之前,必须要先安装好 keil5 以及 CubeMX 等软硬件环境,如果你已经安装完成,请告诉自己:考试现在开始!从CubeMX开始CubeMX是创建工程模板的软件,也是我们比赛时第一个要进行操作的软件。一、选择…...

Java面向对象:接口的学习
本文介绍了Java中接口的基本语法, 什么是接口, java中的接口 语法规则, 接口的使用,接口的特性,如何实现多个接口,接口间的继承,以及抽象类和接口的区别 Java接口的学习一.接口的概念二.Java中的接口1.接口语法规则2.接口的使用3.接口的特性4.实现多个接口5.接口间的继承三.抽象…...

西瓜视频登录页面
题目 代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>登录页面</title><style>td{width: 160px;height: 25px;}img{width: 20px;height: 20px;}.number, .password{background: rgba(0,0,0,.05);}.numbe…...

【springboot】常用快捷键:
Ctrl快捷键介绍Ctrl F在当前文件进行文本查找 (必备)Ctrl R在当前文件进行文本替换 (必备)Ctrl Z撤销 (必备)Ctrl Y删除光标所在行 或 删除选中的行 (必备)Ctrl X剪切光标所在行…...

宝塔控制面板常用Linux命令大全
宝塔面板是站长朋友们常见的一款服务器运维面板,可以通过 Web 端轻松管理服务器,提升运维效率。大家在服务器中安装宝塔面板会用到宝塔面板特定的脚本命令。今天这篇文章为大家整理汇总了宝塔面板常用Linux命令,这样方便大家收藏查找。 1、安…...
C语言实现单链表(超多配图,这下不得不学会单链表了)
目录 一:什么是链表? 二:创建源文件和头文件 (1)头文件 (2)源文件 三:实参和形参 四:一步步实现单向链表 (1)建立一个头指针并置空 (2)打印链表,便于…...
SQL编写优化技巧
一、底层原理 sql慢是因为没有走索引,因此需要添加索引然它走索引联合索引需要匹配最左匹配原则(索引回表)如果查询列超出索引的key, 会导致回表,回表数量多,则会走全表扫描 索引是分聚集索引、非聚集索引…...
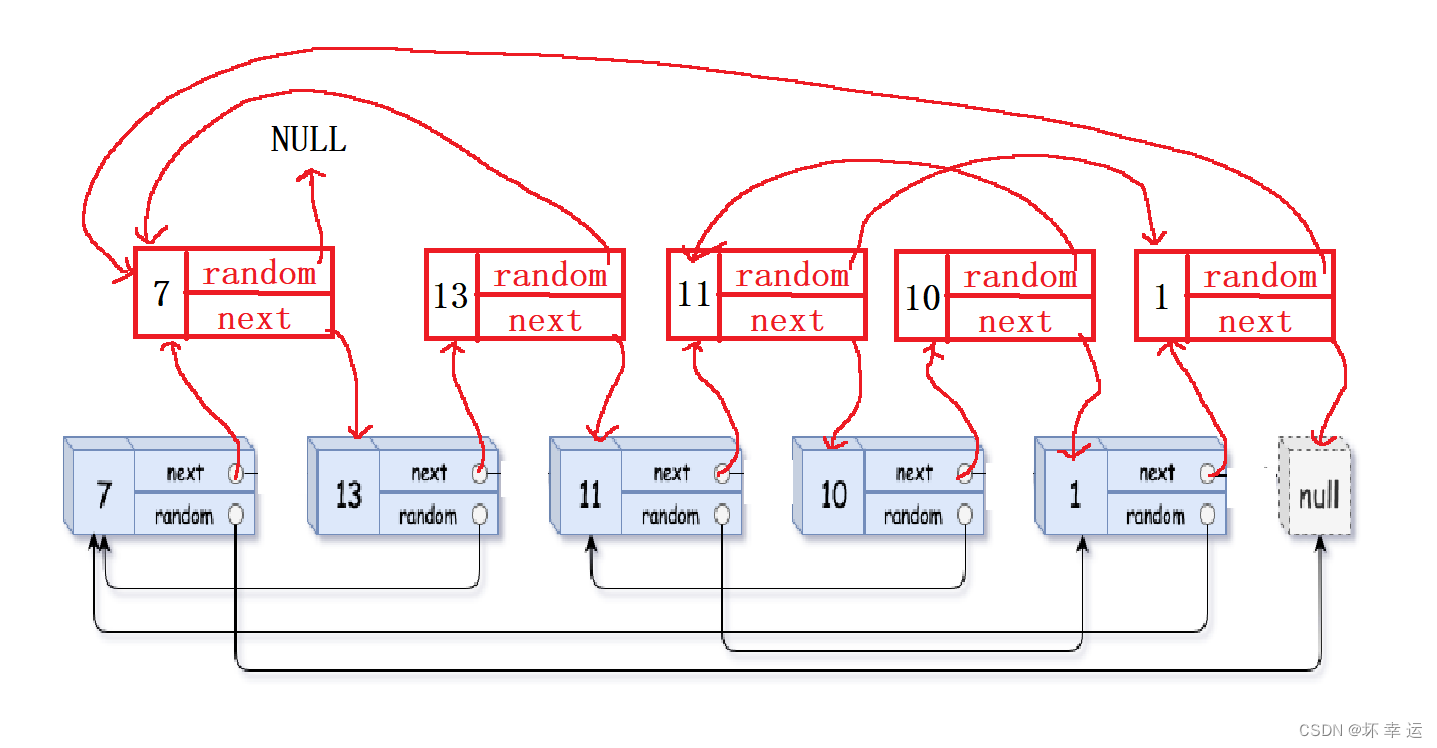
【基础算法】单链表的OJ练习(6) # 复制带随机指针的链表 #
文章目录🍇前言🍎复制带随机指针的链表🍑写在最后🍇前言 本章的链表OJ练习,是最后的也是最难的。对于本题,我们不仅要学会解题的思路,还要能够通过这个思路正确的写出代码,也就是思路…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
