基于深度学习的复杂策略学习
基于深度学习的复杂策略学习(Complex Strategy Learning)是通过深度学习技术,特别是强化学习和模仿学习,来开发和优化解决复杂任务的策略。这类技术广泛应用于自动驾驶、游戏AI、机器人控制和金融交易等领域。以下是对这一领域的系统介绍:
1. 任务和目标
复杂策略学习的主要任务和目标包括:
- 策略优化:开发高效的策略来解决复杂任务,例如导航、控制和决策等。
- 自适应学习:通过学习和适应环境变化,提升系统的智能化水平。
- 多目标优化:在多个目标之间进行权衡,找到最佳策略。
- 长时序依赖:处理具有长时序依赖性的任务,确保策略的长期有效性。
- 实时决策:在动态环境中进行实时决策,确保系统的响应速度和准确性。
2. 技术和方法
2.1 强化学习(Reinforcement Learning, RL)
强化学习是一种通过与环境交互来学习策略的技术,核心思想是通过试错法和奖励机制来优化策略。常用的强化学习算法包括:
- Q-learning:基于值函数的方法,通过更新状态-动作对的值来优化策略。
- 深度Q网络(DQN):将Q-learning与深度神经网络相结合,处理高维度的状态空间。
- 策略梯度方法(Policy Gradient Methods):直接优化策略,通过梯度提升策略的性能。
- REINFORCE:一种基本的策略梯度算法,通过采样轨迹来更新策略。
- 近端策略优化(PPO):一种稳定性更高的策略梯度算法,通过限制策略更新的幅度来提高训练效果。
- 演员-评论家方法(Actor-Critic Methods):结合值函数和策略优化的算法,通过同时更新策略和值函数来提升性能。
- 分层强化学习(Hierarchical Reinforcement Learning, HRL):将任务分解为多个子任务,通过学习子任务的策略来解决复杂任务。
2.2 模仿学习(Imitation Learning)
模仿学习通过学习专家的演示数据来开发策略,常用的方法包括:
- 行为克隆(Behavior Cloning, BC):通过监督学习直接模仿专家的行为。
- 逆强化学习(Inverse Reinforcement Learning, IRL):通过推断专家的奖励函数来优化策略。
- 生成对抗模仿学习(Generative Adversarial Imitation Learning, GAIL):结合生成对抗网络(GAN)和模仿学习,通过对抗训练来优化策略。
2.3 深度神经网络
深度神经网络在复杂策略学习中的应用主要包括:
- 卷积神经网络(CNN):用于处理图像和视频数据,提取高维特征。
- 循环神经网络(RNN):用于处理时间序列数据,捕捉长时序依赖。
- 长短期记忆网络(LSTM):一种特殊的RNN结构,擅长处理长序列数据。
- 变压器模型(Transformer):通过自注意力机制处理大规模数据,提高策略学习的效率和准确性。
3. 应用和评估
3.1 应用领域
基于深度学习的复杂策略学习在多个领域具有重要应用:
- 自动驾驶:开发自动驾驶车辆的导航和决策策略,提高驾驶安全性和效率。
- 游戏AI:开发智能游戏代理,提升游戏体验和挑战性。
- 机器人控制:优化机器人在复杂环境中的控制策略,提高任务完成的准确性和效率。
- 金融交易:开发高频交易策略,优化交易决策,提升投资收益。
- 智能家居:优化智能设备的控制策略,提高用户的生活质量。
3.2 评估指标
评估复杂策略学习系统性能的常用指标包括:
- 奖励值(Reward):衡量策略在任务中的表现,通过累计奖励值评估策略的效果。
- 成功率(Success Rate):衡量策略完成任务的成功率,评估策略的有效性。
- 学习效率(Learning Efficiency):衡量策略学习的速度和效率,通过收敛时间和样本效率评估。
- 鲁棒性(Robustness):衡量策略在不同环境和条件下的稳定性和适应性。
- 计算资源消耗(Resource Consumption):衡量策略学习和执行所需的计算资源,包括时间、内存和计算能力等。
4. 挑战和发展趋势
4.1 挑战
尽管基于深度学习的复杂策略学习取得了显著进展,但仍面临一些挑战:
- 高维度状态空间:处理高维度状态空间和动作空间,确保策略的高效性和准确性。
- 探索-利用权衡:在探索新策略和利用现有策略之间找到平衡,优化策略学习过程。
- 样本效率:提高策略学习的样本效率,减少所需的训练数据和时间。
- 多任务学习:在多任务环境中进行策略学习,提高策略的泛化能力和适应性。
- 安全性和可靠性:确保策略在实际应用中的安全性和可靠性,避免不良行为和决策。
4.2 发展趋势
- 多智能体强化学习(Multi-Agent Reinforcement Learning, MARL):研究多智能体环境中的策略学习,优化智能体之间的协作和竞争。
- 自监督学习(Self-Supervised Learning):通过自监督学习技术,提升策略学习的样本效率和泛化能力。
- 元学习(Meta-Learning):通过元学习技术,提升策略在新任务和新环境中的快速适应能力。
- 人机协作(Human-AI Collaboration):研究人机协作策略,优化智能系统与人类用户之间的交互和协作。
- 强化学习安全性(Safe Reinforcement Learning):研究强化学习的安全性,开发安全可靠的策略,确保实际应用中的安全性。
5. 未来发展方向
- 跨领域应用:将复杂策略学习技术应用于更多领域,如医疗诊断、环境保护和资源管理等。
- 融合多模态数据:结合视觉、听觉、触觉等多模态数据,提高策略学习的全面性和准确性。
- 可解释性研究:开发具有更高可解释性的策略学习模型,提升用户的信任和接受度。
- 高效计算平台:研究高效的计算平台和算法,加速策略学习和推理过程。
综上所述,基于深度学习的复杂策略学习在自动驾驶、游戏AI、机器人控制、金融交易和智能家居等领域具有广泛的应用前景,并且在高维度状态空间处理、探索-利用权衡、样本效率、多任务学习和安全性等方面面临重要挑战。通过多智能体强化学习、自监督学习、元学习、人机协作和安全性研究等新技术的引入,将进一步推动这一领域的发展和应用。
相关文章:

基于深度学习的复杂策略学习
基于深度学习的复杂策略学习(Complex Strategy Learning)是通过深度学习技术,特别是强化学习和模仿学习,来开发和优化解决复杂任务的策略。这类技术广泛应用于自动驾驶、游戏AI、机器人控制和金融交易等领域。以下是对这一领域的系…...
)
【Golang 面试 - 进阶题】每日 3 题(一)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...
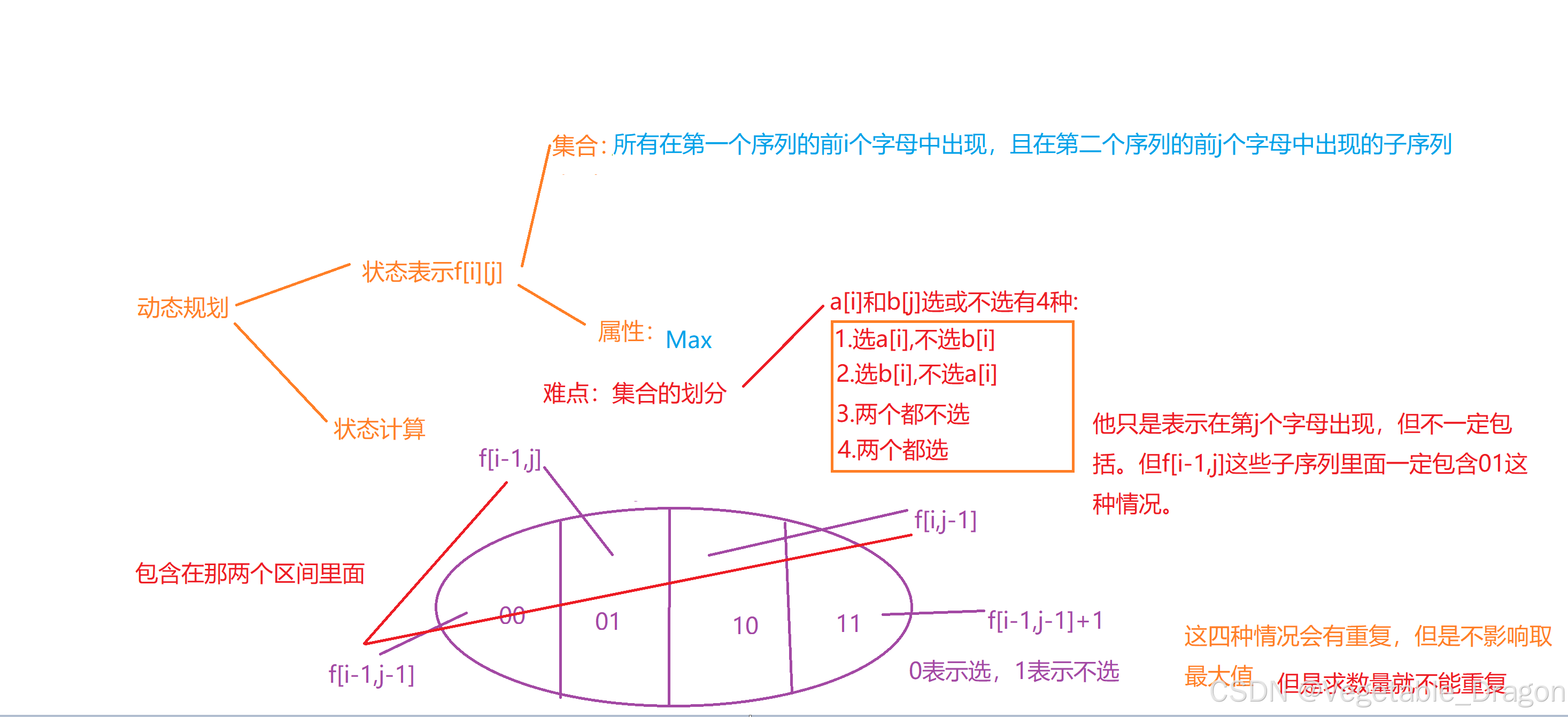
周报 Week 3:
补题链接: Week 3 DAY 1-CSDN博客 河南萌新联赛2024第(二)场:南阳理工学院-CSDN博客 Week 3 DAY 5:-CSDN博客 Week 3 DAY 6-CSDN博客 这周题单是动态规划——(背包问题,线性dp):…...

开源消息队列比较
目录 1. Apache Kafka 1.1安装步骤 1.1.1使用Docker安装 1.1.1手动安装 1.2 C#使用示例代码 1.2.1 安装Confluent.Kafka 1.2.2生产者代码示例 1.2.3消费者代码示例 1.3特点 1.4使用场景 2. RabbitMQ 2.1安装步骤 2.1.1使用Docker安装 2.1.2手动安装 2.2 C#使用示…...
【前端逆向】最佳JS反编译利器,原来就是chrome!
有时候需要反编译别人的 min.js。 比如简单改库、看看别人的 min,js 干了什么,有没有重复加载?此时就需要去反编译Javascript。 Vscode 里面有一些反编译插件,某某Beautify等等。但这些插件看人品,运气不好搞的话,反…...

微信小程序根据动态权限展示tabbar
微信小程序自定义 TabBar 后根据权限动态展示tabbar 在微信小程序开发中,自定义 TabBar 可以让应用更具灵活性和个性化。特别是在用户根据不同权限展示不同的 TabBar 内容时,正确的实现方法能够提升用户体验。本篇文章将分享如何使用事件总线实现权限变动时动态更新自定义 T…...
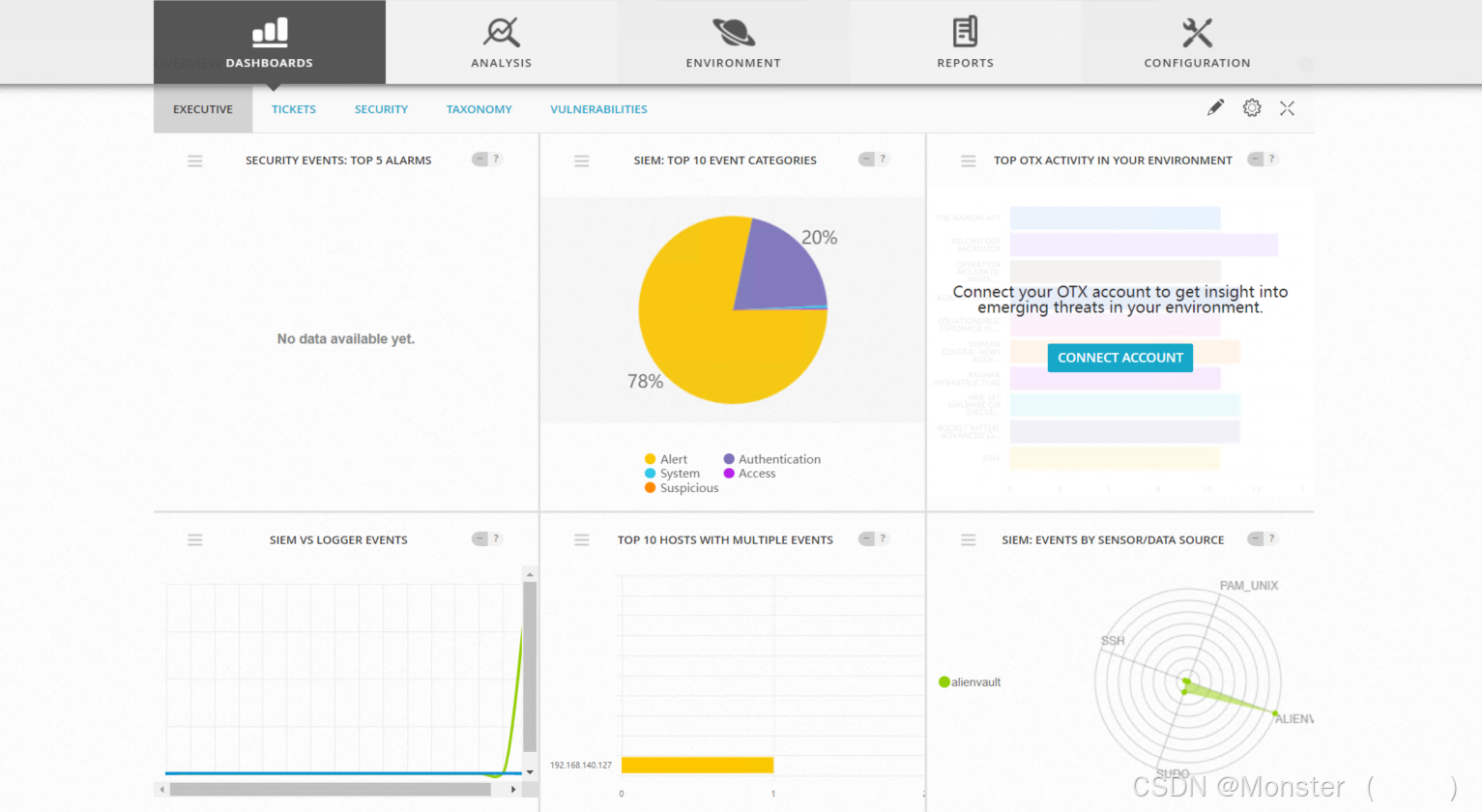
开源安全信息和事件管理(SIEM)平台OSSIM
简介 OSSIM,开源安全信息和事件管理(SIEM)产品,提供了经过验证的核心SIEM功能,包括事件收集、标准化和关联。 OSSIM作为一个开源平台,具有灵活性和可定制性高的优点,允许用户根据自己的特定需…...

【DP】01背包
算法-01背包 前置知识 DP 思路 01背包一般分为两种,不妨叫做价值01背包和判断01背包。 价值01背包 01背包问题是这样的一类问题:给定一个背包的容量 m m m 和 n n n 个物品,每个物品有重量 w w w 和价值 v v v,求不超过背…...

50、PHP 实现选择排序
题目: PHP 实现选择排序 描述: n个记录的文件的直接选择排序可经过n-1趟直接选择排序得到有序结果:(1)初始状态:无序区为R[1…n],有序区为空。(2)第1趟排序在无序区R[1…n]中选出关键字最小的记录R[k],将…...

17.延迟队列
介绍 延迟队列,队列内部是有序的,延迟队列中的元素是希望在指定时间到了以后或之前取出和处理。 死信队列中,消息TTL过期的情况其实就是延迟队列。 使用场景 1.订单在十分钟内未支付则自动取消。 2.新创建的店铺,如果十天内没…...

KCache-go本地缓存,支持本地缓存过期、缓存过期自维护机制。
GitHub - kocor01/kcache: go 本地缓存解决方案,支持本地缓存过期、缓存过期自维护机制。 最近系统并发很高,单接口10W的 QPS,对 redis 压力很大,大量的热KEY导致 redis 分片CPU资源经常告警。计划用 go 本地缓存缓解 redis 的压…...

斯坦福UE4 C++课学习补充 14:UMG-优化血量条
文章目录 一、优化执行效率二、简单脉冲动画 一、优化执行效率 绑定事件需要每一帧检查绑定对象是否有变化,势必造成CPU资源的浪费,因此优化执行效率的思路是:UI组件不再自行每帧查询血量,而是让血量自己在发生变化的同时通知UI进…...

在生信分析中大家需要特别注意的事情
在生信分析中大家需要特别注意的事情 标准的软件使用和数据分析流程 1. 先看我的b站教学视频 2. 先从我的百度网盘把演示数据集下载下来,先把要运行的模块的演示数据集先运行一遍 3. 前两步都做完了,演示数据集也运行成功了,并且知道了软件…...

Java工厂模式详解:方法工厂模式与抽象工厂模式
Java工厂模式详解:方法工厂模式与抽象工厂模式 一、引言 在Java开发中,设计模式是解决常见软件设计问题的一种有效方式。工厂模式作为创建型设计模式的一种,提供了灵活的对象创建机制,有助于降低代码的耦合度,提高系…...

springSecurity学习之springSecurity用户单设备登录
用户只能单设备登录 有时候在同一个系统中,只允许一个用户在一个设备登录。 之前的登陆者被顶掉 将最大会话数设置为1就可以保证用户只能同时在一个设备上登录 Override protected void configure(HttpSecurity http) throws Exception {http..anyRequest().aut…...

微信小程序实现聊天界面,发送功能
.wxml <scroll-view scroll-y"true" style"height: {{windowHeight}}px;"><view wx:for"{{chatList}}" wx:for-index"index" wx:for-item"item" style"padding-top:{{index0?30:0}}rpx"><!-- 左…...

【强化学习的数学原理】课程笔记--5(值函数近似,策略梯度方法)
目录 值函数近似一个例子TD 算法的值函数近似形式Sarsa, Q-learning 的值函数近似形式Deep Q-learningexperience replay 策略梯度方法(Policy Gradient)Policy Gradient 的目标函数目标函数 1目标函数 2两种目标函数的同一性 Policy Gradient 目标函数的…...

前端Long类型精度丢失:后端处理策略
文章目录 精度丢失的具体原因解决方法1. 使用 JsonSerialize 和 ToStringSerializer2. 使用 JsonFormat 注解3. 全局配置解决方案 结论 开发商城管理系统的品牌管理界面时,发现一个问题,接口返回品牌Id和页面展示的品牌Id不一致,如接口返回的…...

C++ | Leetcode C++题解之第300题最长递增子序列
题目: 题解: class Solution { public:int lengthOfLIS(vector<int>& nums) {int len 1, n (int)nums.size();if (n 0) {return 0;}vector<int> d(n 1, 0);d[len] nums[0];for (int i 1; i < n; i) {if (nums[i] > d[len])…...
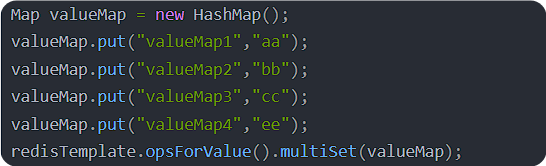
springboo 整合 redis
springBoot 整合 redis starter启动依赖。—包含自动装配类—完成相应的装配功能。 引入依赖 <!--引入了redis整合springboot 的依赖--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis&…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
