【C++的剃刀】我不允许你还不会AVL树

学习编程就得循环渐进,扎实基础,勿在浮沙筑高台
循环渐进Forward-CSDN博客
Hello,这里是kiki,今天继续更新C++部分,我们继续来扩充我们的知识面,我希望能努力把抽象繁多的知识讲的生动又通俗易懂,今天要讲的是C++AVL树~
目录
循环渐进Forward-CSDN博客
AVL树的概念
AVL树节点的定义
AVL树的插入
AVL树的旋转
AVL树的验证
AVL树的删除(了解)
AVL树的性能
AVL树的概念
二叉搜索树虽可以缩短查找的效率,但 如果数据有序或接近有序二叉搜索树将退化为单支树,查 找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种解决上述问题的方法: 当向二叉搜索树中插入新结点后,如果能保证每个结点的左右 子树高度之差的绝对值不超过 1( 需要对树中的结点进行调整 ),即可降低树的高度,从而减少平均搜索长度。
它的左右子树都是 AVL 树左右子树高度之差 ( 简称平衡因子 ) 的绝对值不超过 1(-1/0/1)

AVL树节点的定义
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子
};AVL树的插入
1. 按照二叉搜索树的方式插入新节点2. 调整节点的平衡因子
bool Insert(const T& data)
{
while (pParent){// 更新双亲的平衡因子if (pCur == pParent->_pLeft)pParent->_bf--;elsepParent->_bf++;// 更新后检测双亲的平衡因子if (0 == pParent->_bf){ break;}else if (1 == pParent->_bf || -1 == pParent->_bf){// 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲
为根的二叉树// 的高度增加了一层,因此需要继续向上调整pCur = pParent;pParent = pCur->_pParent;}else{if(2 == pParent->_bf){// ...}else{// ...}}}return true;
}AVL树的旋转



// 旋转之前,60的平衡因子可能是-1/0/1,旋转完成之后,根据情况对其他节点的平衡因子进
行调整
void _RotateLR(PNode pParent)
{PNode pSubL = pParent->_pLeft;PNode pSubLR = pSubL->_pRight;// 旋转之前,保存pSubLR的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节
点的平衡因子int bf = pSubLR->_bf;// 先对30进行左单旋_RotateL(pParent->_pLeft);// 再对90进行右单旋_RotateR(pParent);if(1 == bf)pSubL->_bf = -1;else if(-1 == bf)pParent->_bf = 1;
}
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑1. pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR1、当pSubR的平衡因子为1时,执行左单旋2、当pSubR的平衡因子为-1时,执行右左双旋2. pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL1、当pSubL的平衡因子为-1是,执行右单旋2、当pSubL的平衡因子为1时,执行左右双旋旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
AVL树的验证
1. 验证其为二叉搜索树1、如果中序遍历可得到一个有序的序列,就说明为二叉搜索树2. 验证其为平衡树1、每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)2、节点的平衡因子是否计算正确
int _Height(PNode pRoot);
bool _IsBalanceTree(PNode pRoot)
{// 空树也是AVL树if (nullptr == pRoot) return true;// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差int leftHeight = _Height(pRoot->_pLeft);int rightHeight = _Height(pRoot->_pRight);int diff = rightHeight - leftHeight;
// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != pRoot->_bf || (diff > 1 || diff < -1))return false;// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree(pRoot->_pLeft) && _IsBalanceTree(pRoot-
>_pRight);}AVL树的删除(了解)
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即$log_2 (N)$。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
学习编程就得循环渐进,扎实基础,勿在浮沙筑高台
相关文章:

【C++的剃刀】我不允许你还不会AVL树
学习编程就得循环渐进,扎实基础,勿在浮沙筑高台 循环渐进Forward-CSDN博客 Hello,这里是kiki,今天继续更新C部分,我们继续来扩充我们的知识面,我希望能努力把抽象繁多的知识讲的生动又通俗易懂,今天要…...

React搭建Vite项目及各种项目配置
1. 创建Vite项目 在操作系统的命令终端,输入以下命令: yarn create vite 输入完成以后输入项目名称、选择开发框架,选择开发语言,如下图所示,即可完成项目创建。 注意事项: 1. Node版本必须符合要求&…...

Linux Vim教程:多文件编辑与窗口管理
目录 1. 多文件编辑基础 1.1 缓冲区管理 1.2 标签页管理 1.3 分屏管理 2. 多文件编辑的高级技巧 2.1 同时编辑多个文件 2.2 使用会话 2.3 使用寄存器 3. 窗口管理的实用技巧 3.1 窗口调整 3.2 窗口排列 3.3 快速切换 4. 使用插件增强多文件编辑与窗口管理 4.1 NE…...

C语言进阶 11.结构体
C语言进阶 11.结构体 文章目录 C语言进阶 11.结构体11.1. 枚举11.2. 结构类型11.3. 结构与函数11.4. 结构中的结构11.5. 类型定义11.6. 联合11.7. PAT11-0. 平面向量加法(10)11-1. 通讯录的录入与显示(10) 11.1. 枚举 常量符号化: 用符号而不是具体的数字表示程序中的数字 cons…...

Vue--解决error:0308010C:digital envelope routines::unsupported
原文网址:Vue--解决error:0308010C:digital envelope routines::unsupported_IT利刃出鞘的博客-CSDN博客 简介 本文介绍如何解决node.js在运行Vue项目时的报错:error:0308010C:digital envelope routines::unsupported。 问题描述 使用node.js运行Vu…...

go-kratos 学习笔记(6) 数据库gorm使用
数据库是项目的核心,数据库的链接数据是data层的操作,选择了比较简单好用的gorm作为数据库的工具;之前是PHP开发,各种框架都是orm的操作;gorm还是很相似的,使用起来比较顺手 go-kratos官网的实例是ent&…...

记录:vite打包报错 error during build: Error: Parse error @:1:1
vant从3升级到4后,本地运行没问题, 但是打包就会报如下错误:error during build: Error: Parse error :1:1 一直以为是vant的问题,各种升级,替换插件,发现没什么用, 网上搜索了下,…...

Python 消费Kafka手动提交 批量存入Elasticsearch
一、第三方包选择 pip install kafka,对比了kafka和pykafka,还是选择kafka,消费速度更快pip install elasticsearch7.12.0(ES版本) 二、创建es连接对象 from elasticsearch import Elasticsearch from elasticsearch.helpers import bulkc…...

oracle 基础知识表的主键
一、表的约束条件 •约束条件是施加在表的字段上的一组限制条件,它使得只有符合限制条件要求的数据才能输入表。 •保证了表中的数据的正确性 i.约束条件包括了:非空和唯一和核对,即not null 和unique 和check null的含义:不确定 3个人去捡苹…...

opencascade AIS_MouseGesture AIS_MultipleConnectedInteractive源码学习
AIS_MouseGesture //! 鼠标手势 - 同一时刻只能激活一个。 enum AIS_MouseGesture { AIS_MouseGesture_NONE, //!< 无激活手势 // AIS_MouseGesture_SelectRectangle, //!< 矩形选择; //! 按下按钮开始,移动鼠标定义矩形&…...
Unity Apple Vision Pro 开发:如何把 PolySpatial 和 Play To Device 的版本从 1.2.3 升级为 1.3.1
XR 开发社区: SpatialXR社区:完整课程、项目下载、项目孵化宣发、答疑、投融资、专属圈子 📕教程说明 本教程将介绍如何把 Unity 的 PolySpatial 和 Play To Device 版本从 1.2.3 升级为 1.3.1。 📕Play To Device 软件升级 ht…...

大数据时代,区块链是如何助力数据开放共享的?
在大数据时代,区块链技术以其独特的优势,为数据开放共享提供了强有力的支持。以下是区块链助力数据开放共享的几个主要方面: 1. 增强数据安全性与隐私保护 加密安全:区块链技术采用先进的加密算法,如国密非对称加密技…...

睿抗2024省赛----RC-u4 章鱼图的判断
题目 对于无向图 G(V,E),我们将有且只有一个环的、大于 2 个顶点的无向连通图称之为章鱼图,因为其形状像是一个环(身体)带着若干个树(触手),故得名。 给定一个无向图,请你判断是不…...

py2exe,一个神奇的 Python 库
在众多Python打包工具中,py2exe无疑是一款出色的选择。它能够将Python脚本转换成可在Windows平台上独立运行的可执行文件,极大地方便了程序的分发与部署。本文将深入探讨py2exe的特性和使用方法,让你在创建桌面应用程序时更加游刃有余。 安装…...

博途PLC网络连接不上
博途PLC网络连接不上其中的一个原因就是网线接触不好,各种原因都试了,任然连接不上,大家可以把网线拔下,重新插拔或者直接更换一根网线。 1、无线网络网段和PLC连接网段冲突 。。。。...

哪个邮箱最安全最好用啊
企业邮箱安全至关重要,需保护隐私、防财务损失、维护通信安全、避免纠纷,并维持业务连续性。哪个企业邮箱最安全好用呢?Zoho企业邮箱,采用加密技术、反垃圾邮件和病毒保护,支持多因素认证,确保数据安全合规…...

企业微信开发智能升级:AIGC技术赋能,打造高效沟通平台
文章目录 一、AIGC在企业微信开发中的核心价值1. 智能化客服体验2. 自动化工作流程3. 个性化内容推荐4. 深度数据分析与洞察 二、使用AIGC进行企业微信开发的实践路径1. 需求分析与场景定义2. 技术选型与平台搭建3. 模型训练与调优4. 接口对接与功能集成5. 测试与优化 《企业微…...
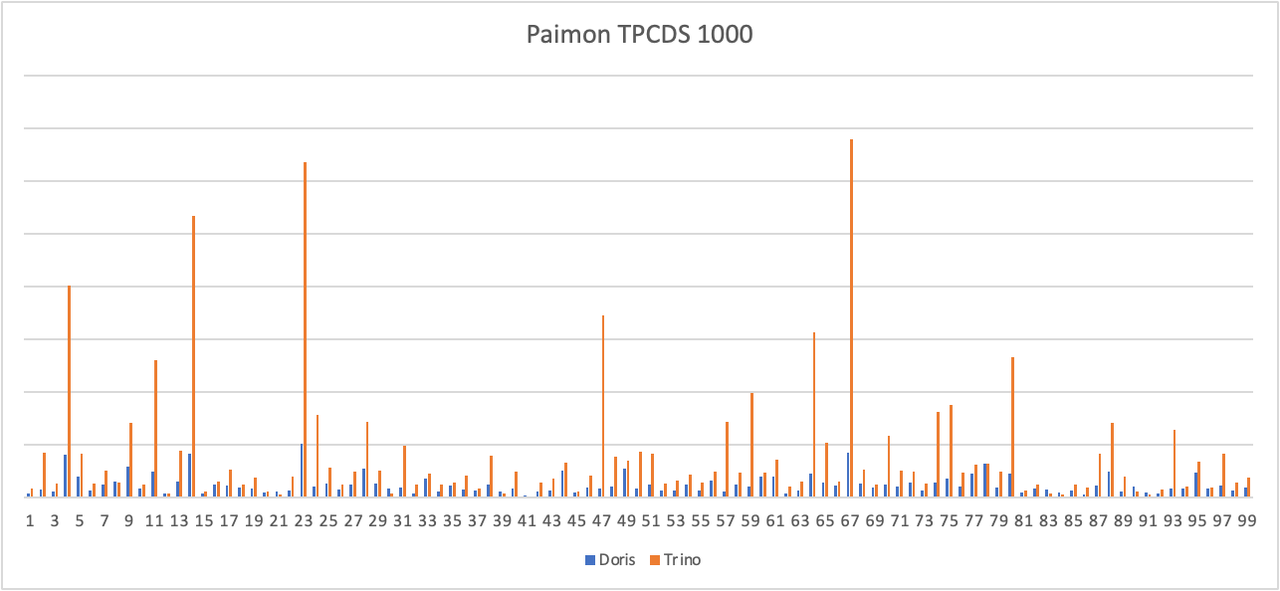
Apache Doris + Paimon 快速搭建指南|Lakehouse 使用手册(二)
湖仓一体(Data Lakehouse)融合了数据仓库的高性能、实时性以及数据湖的低成本、灵活性等优势,帮助用户更加便捷地满足各种数据处理分析的需求。在过去多个版本中,Apache Doris 持续加深与数据湖的融合,已演进出一套成熟…...

Inno setup pascal编码下如何美化安装界面支持带边框,圆角,透明阴影窗口
inno setup自带的安装界面太老套了,如何实现类似网易,微信那种带界面的安装?一般有两种思路:提供一个单独的下载器,然后通过下载器将你用innosetup 打包后的软件下载下来,然后,静默安装这个包&a…...

SQL语句(以MySQL为例)——单表、多表查询
笛卡尔积(或交叉连接): 笛卡尔乘积是一个数学运算。假设我有两个集合 X 和 Y,那么 X 和 Y 的笛卡尔积就是 X 和 Y 的所有可能组合,也就是第一个对象来自于 X,第二个对象来自于 Y 的所有可能。组合的个数即为两个集合中…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
