B4005 [GESP202406 四级] 黑白方块 【暴力枚举】【前缀和】
#include<bits/stdc++.h>
using namespace std;
int n,m,ans,tmp;
char mp[20][20];
int cheak(int a,int b,int c,int d){//a<=c b<=dint cnt=0;//枚举矩阵中的每个点 for(int i=a;i<=c;i++)for(int j=b;j<=d;j++)if(mp[i][j]=='1') cnt++;//统计黑格的个数 return 2*cnt==(c-a+1)*(d-b+1);//如果黑格子的数量为总数的一半,则为平衡矩阵
}int main(){cin>>n>>m;//输入二维矩阵没有空格,一定要用char[][] for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>mp[i][j];//不降原则枚举矩形的左上角(i,j)和右下角 (ii,jj)for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) {for (int ii = i; ii <= n; ii++) {for (int jj = j; jj <= m; jj++) {if (cheak(i, j, ii, jj)){//cheak检查当前矩阵是否是平衡矩阵 //利用 (ii - i + 1) * (jj - j + 1)求出矩阵中点的总数 ans = max(ans, (ii - i + 1) * (jj - j + 1));}}}}}cout << ans << endl;return 0;
}
以上为暴力枚举,以下为二维前缀和
#include<bits/stdc++.h>
using namespace std;
int n,m,ans,tmp,sum[20][20];
char mp[20][20];
int cheak(int a,int b,int c,int d){//a<=c b<=d //利用前缀和获得区间和(黑格子的数量) int cnt=sum[c][d]-sum[a-1][d]-sum[c][b-1]+sum[a-1][b-1];return 2*cnt==(c-a+1)*(d-b+1);//如果黑格子的数量为总数的一半,则为平衡矩阵
}int main(){cin>>n>>m;//输入二维矩阵没有空格,一定要用char[][] for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>mp[i][j];//求黑格子前缀和 for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){if(mp[i][j]=='1') sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+1;else sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+0;}//不降原则枚举矩形的左上角(i,j)和右下角 (ii,jj)for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) {for (int ii = i; ii <= n; ii++) {for (int jj = j; jj <= m; jj++) {if (cheak(i, j, ii, jj)){//cheak检查当前矩阵是否是平衡矩阵 //利用 (ii - i + 1) * (jj - j + 1)求出矩阵中点的总数 ans = max(ans, (ii - i + 1) * (jj - j + 1));}}}}}cout << ans << endl;return 0;
}相关文章:

B4005 [GESP202406 四级] 黑白方块 【暴力枚举】【前缀和】
#include<bits/stdc.h> using namespace std; int n,m,ans,tmp; char mp[20][20]; int cheak(int a,int b,int c,int d){//a<c b<dint cnt0;//枚举矩阵中的每个点 for(int ia;i<c;i)for(int jb;j<d;j)if(mp[i][j]1) cnt;//统计黑格的个数 return 2*cnt(c-a1…...

深度学习趋同性的量化探索:以多模态学习与联合嵌入为例
深度学习趋同性的量化探索:以多模态学习与联合嵌入为例 参考文献 据说是2024年最好的人工智能论文,是否有划时代的意义? [2405.07987] The Platonic Representation Hypothesis (arxiv.org) arxiv.org/abs/2405.07987 趋同性的量化表达 …...

决策树与随机森林:比较与应用场景分析
决策树与随机森林:比较与应用场景分析 引言 决策树和随机森林是机器学习中广泛使用的两种算法,因其简单性和强大的功能而被广泛采用。决策树是一种树形结构的决策模型,易于理解和解释。随机森林则是通过集成多棵决策树来提高预测性能的模型…...

C#用Aspose.Cells导出Excel,.NET导出Excel
ASP.NET MVC 控制器里面Action处理,下载文件,输出文件流 public async Task<ActionResult> ExportNewsAuthorFee(string deptId, DateTime? startDate, DateTime? endDate){if (startDate null){startDate DateTime.Parse(DateTime.Now.Year …...

天猫番茄品类TOP1,复购率超40%,「一颗大」如何策划极致产品力?
桔子要买什么品牌?桃子买什么品牌?土豆买什么品牌?过去人们购买农产品几乎没有品牌意识。但近年来可能某些人买猕猴桃时会考虑佳沛,这是一个在全球达到30%猕猴桃市场的新西兰品牌。与此类似,一个国产品牌「一颗大™」正…...

Docker搭建私有仓库harbor(docker 镜像仓库搭建)
Harbor介绍 Docker容器应用的开发和运行离不开可靠的镜像管理,虽然Docker官方也提供了公共的镜像仓库,但是从安全和效率等方面考虑,部署我们私有环境内的Registry也是非常必要的。Harbor是由VMware公司开源的企业级的Docker Registry管理项目…...

面试题:MySQL 索引
1. 谈一下你对于MySQL索引的理解?(为什么MySQL要选择B+树来存储索引) MySQL的索引选择B+树作为数据结构来进行存储,使用B+树的本质原因在于可以减少IO次数,提高查询的效率,简单来说就是可以保证在树的高度不变的情况下存储更多的数据: IO效率的提高:在MySQL数据库中,…...

云计算day13
一、Git 概述 Git 是一种分布式版本控制系统,用于跟踪和管理代码的变更。它是由 Linus Torvalds 创建的,最初被设计用于 Linux 内核的开发。Git 允许开发 人员跟踪和管理代码的版本,并且可以在不同的开发人员之间进行协作。 Github 用的就…...

2024年孝感中级职称报名开始了吗?
2024年孝感中级职称申报终于开始了,之前参加过水测的小伙伴们,开始准备评审了 2024年孝感本批次申报时间:中级、初级职称网上申报时间:2024年8月1日至8月31日。 注意:个人通过“湖北省职称评审管理信息系统”申报,须先…...

RAG技术之Router
Router有什么用? 在RAG应用中,Router可以帮助我们基于用户的查询意图来决定使用何种数据类型或数据源,比如是否需要进行语义检索、是否需要进行text2sql查询,是否需要用function call来进行API调用。 Router也可以根据用户的查询…...

linux系统通过修改sudo文件使普通用户拥有类似root用户权限
说明:普通用户要想拥有root权限,如果不在sudo文件里配置就算把该用户加到wheel组(root用户所在的组)也不行。 要想通过在命令前加上sudo使得该用户以root权限执行命令,需要修改/etc/sudoers文件。 (如果通…...
基于PyCharm在Windows系统上远程连接Linux服务器中Docker容器进行Python项目开发与部署
文章目录 摘要项目结构项目开发项目上线参考文章 摘要 本文介绍了如何在Windows 10系统上使用PyCharm专业版2024.1,通过Docker容器在阿里云CentOS 7.9服务器上进行Python项目的开发和生产部署。文章详细阐述了项目结构的搭建、PyCharm的使用技巧、以及如何将开发项…...

TypeScript学习篇-类型介绍使用、ts相关面试题
文章目录 基础知识基础类型: number, string, boolean, object, array, undefined, void(代表该函数没有返回值)enum(枚举): 定义一个可枚举的对象typeinterface联合类型: |交叉类型: &any 类型null 和 undefinednullundefined never类型 面试题及实战1. 你觉得使用ts的好处…...
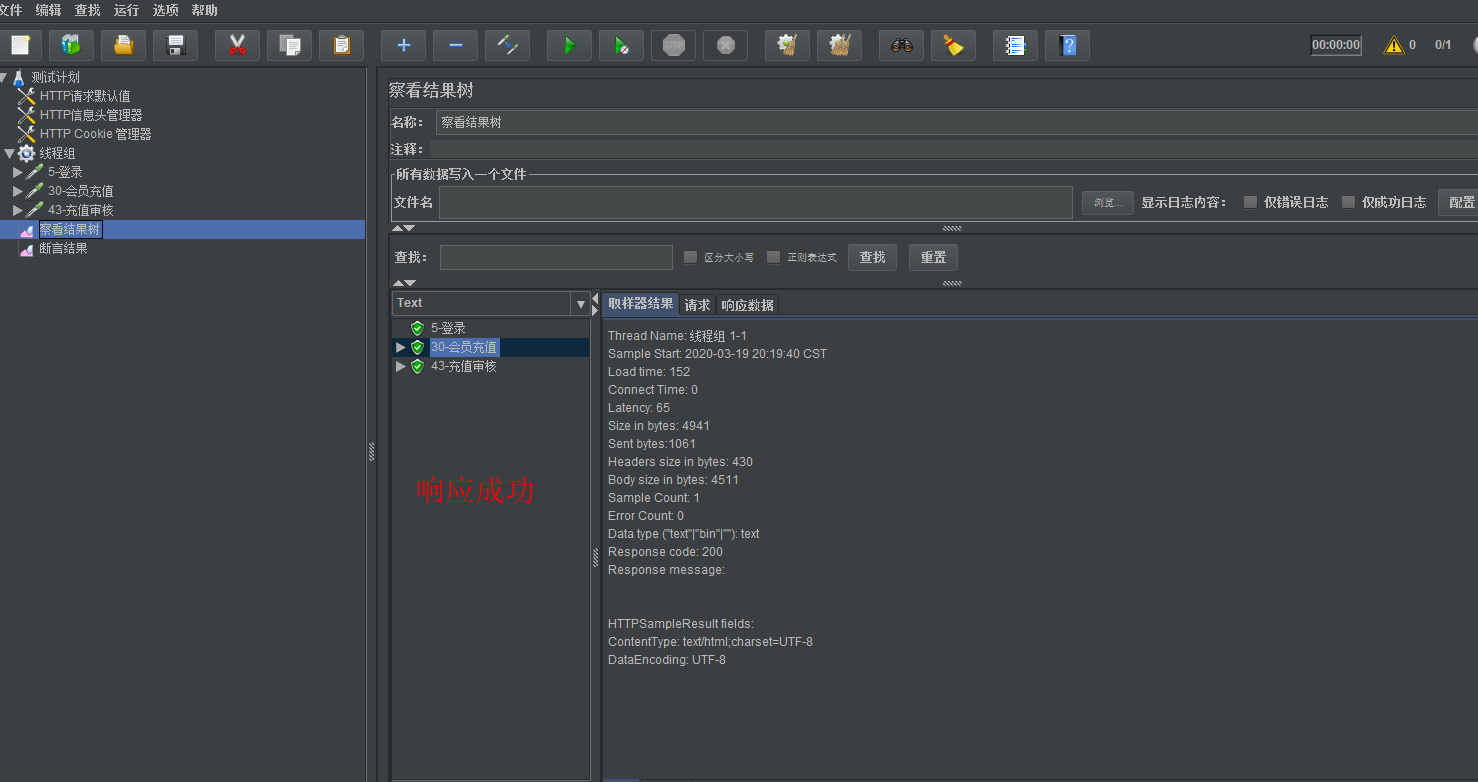
超详细!Jmeter性能测试
前言 性能测试是一个全栈工程师/架构师必会的技能之一,只有学会性能测试,才能根据得到的测试报告进行分析,找到系统性能的瓶颈所在,而这也是优化架构设计中重要的依据。 测试流程: 需求分析→环境搭建→测试计划→脚…...

C语言经典习题24
文件操作习题 一 编程删除从C盘home文件夹下data.txt文本文件中所读取字符串中指定的字符,该指定字符由键盘输入,并将修改后的字符串以追加方式写入到文本文件C:\home\data.txt中。 #include<stdio.h> main() { char s[100],ch; int i;…...
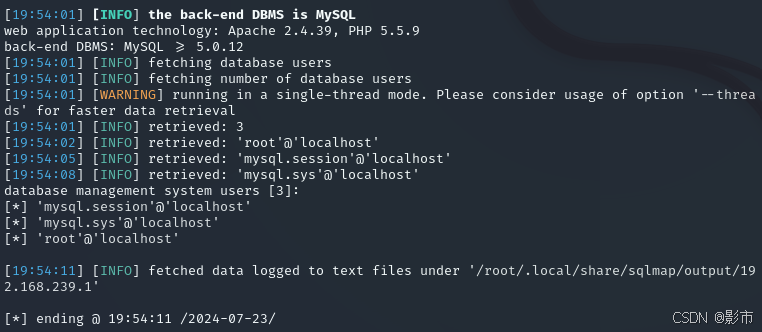
SQL labs-SQL注入(三,sqlmap使用)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。 引言: 盲注简述:是在没有回显得情况下采用的注入方式,分为布尔盲注和时间盲注。 布尔盲注:布尔仅有两种形式,ture&#…...
统一认证与单点登录:简明概述与应用
1. 统一认证概述 统一认证是一种身份验证机制,允许用户使用一个账户来访问多个系统和应用程序。它的主要目标是简化用户的登录过程,提高安全性,并减少管理开销。统一认证通过集中管理用户信息,使得用户只需一次认证即可访问不同的…...

MSPM0G3507学习笔记1:开发环境_引脚认识与点灯
今日速通一款Ti的单片机用于电赛:MSPM0G3507 这里默认已经安装好了Keil5_MDK 首先声明一下: 因为是速成,所以需要一定单片机学习基础,然后我写的也不会详细,这个专栏的笔记也就是自己能看懂就行的目标~~~ 文章提供测试代码解…...

使用法国云手机进行面向法国的社媒营销
在当今数字化和全球化的时代,社交媒体已经成为企业营销和拓展市场的重要工具。对于想进入法国市场的企业来说,如何在海外社媒营销中脱颖而出、抓住更多的市场份额,成为了一个关键问题。法国云手机正为企业提供全新的营销工具,助力…...
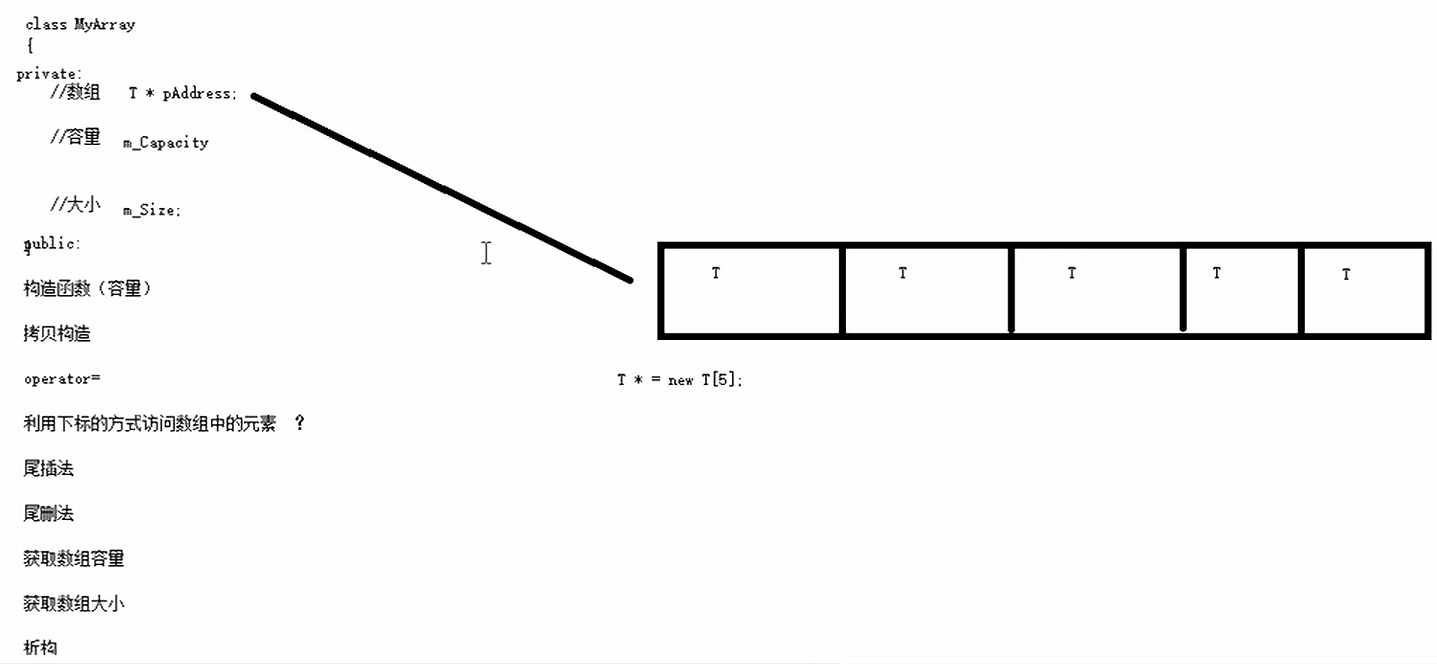
C++学习笔记——模板
学习视频 文章目录 模板的概念函数模板函数模板语法函数模板注意事项函数模板案例普通函数与函数模板的区别普通函数与函数模板的调用规则模板的局限性 类模板类模板与函数模板区别类模板中成员函数创建时机类模板对象做函数参数类模板与继承类模板成员函数类外实现类模板分文件…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
