Matlab arrayfun 与 bsxfun——提高编程效率的利器!
许多人知道 MATLAB 向量化编程,少用 for 循环 可以提高代码运行效率,但关于代码紧凑化编程, arrayfun 与 bsxfun 两个重要函数却鲜有人能够用好,今天针对这两个函数举例说明其威力。
Matlab arrayfun
概述
arrayfun 是 Matlab 中的一个强大函数,它允许用户对数组中的每个元素应用一个指定的函数,并返回一个新的数组,该数组包含了函数对每个元素应用后的结果。这使得对数组进行逐元素操作变得非常灵活和方便,无需编写循环语句。
测试目的
本测试文档旨在展示 arrayfun 函数的多种巧妙用法,包括基本用法、匿名函数的应用、多维数组的处理以及与其他函数的结合使用,以全面理解其功能和效率。
- 先看下面两个基本操作
A = 1:5;
B = arrayfun(@(x) x^2, A);
disp(B);A = -5:5;
B = arrayfun(@(x) x > 0, A);
disp(B);
这两个操作中,arrayfun 提供了便利的逐元素操作方式,但在处理大型数组时,直接利用 Matlab 的内置数组向量化操作(如 +, -, .*, ./ 等)通常会有更好的性能。
- 再看下面这个操作:
[J,I]=meshgrid(1:10);
al=arrayfun(@(ii,jj) integral2(@(u,v)sin(u).*sqrt(v),0,ii,0,jj),I,J);
这段代码在MATLAB环境中执行了一个二维数值积分的计算,具体地,它计算了函数
f ( u , v ) = s i n ( u ) ⋅ v f(u,v)=sin(u)⋅ \sqrt{v} f(u,v)=sin(u)⋅v
在由点 (0, 0) 到点 (ii, jj) 形成的矩形区域上的积分,其中 (ii, jj) 遍历了一个由 meshgrid 函数生成的 10x10 网格的坐标点。让我们逐步解释这段代码的各个部分:
al=arrayfun(@(ii,jj)integral2(@(u,v)sin(u).*sqrt(v),0,ii,0,jj),I,J);
这行代码是代码的核心,它使用了 arrayfun 函数来对 I 和 J 数组中的每个 (ii, jj) 对执行一个函数。这个函数是一个匿名函数,它本身调用了 integral2 函数来执行二维数值积分。
integral2(@(u,v)sin(u).*sqrt(v),0,ii,0,jj) 调用 integral2 来计算函数 f(u, v) = \sin(u) \cdot \sqrt{v} 在矩形区域 [0, ii] x [0, jj] 上的积分。这里,@(u,v)sin(u).*sqrt(v) 定义了被积分的函数,而 0, ii, 0, jj 指定了积分的边界。
arrayfun 函数将这个 integral2 调用应用到 I 和 J 数组的每一个 (ii, jj) 对上,并将结果存储在数组 al 中。因此,al 是一个 10x10 的数组,其中 al(i,j) 存储了函数 f(u, v) 在矩形区域 [0, I(i,j)] x [0, J(i,j)] 上的积分值。
灵活性:这种方法允许用户轻松地对不同区域的函数进行积分,而无需手动编写多个积分调用。通过改变 meshgrid 函数的参数,可以轻松地调整积分的区域大小和形状。
显然这段代码是向量化编程难以执行的,而靠 arrayfun 函数两行搞定.
bsxfun(binary singleton expansion function )
概述
bsxfun是MATLAB中的一个函数,它允许对两个数组进行逐元素操作,同时自动扩展(或广播)较小的数组以匹配较大数组的维度。这使得在不需要显式循环的情况下执行复杂的数组操作成为可能,提高了代码的效率和简洁性。
测试案例
bsxfun 简单的函数操作见帮助文档,这里我们给一个高级的测试案例,展示了bsxfun的妙用:
- 对两个二维数组每一行求差集
MATLAB 目前只能对一维数组求差集,高维的话用 for loop 效率偏低。对于下面这种两个数组每一列只有一个不同元素的矩阵,对每一列求差集,完全可以不用 for loop:
%例如下面对 A,B 每一行求差集
% A = [1,2,3,4,5; 8,4,7,9,6];
% B = [2,3; 4,9];
% mask = all(bsxfun(@ne,A,permute(B,[1 3 2])),3);
% At = A.'; %//'
% out = reshape(At(mask.'),[],size(A,1)).';% ---------------------------------------------------
%下面算例对两个矩阵每一列求差集
B=[4 4 7 7 7 7 6 6 6 6 6 63 9 9 5 9 8 2 9 4 4 9 89 2 3 9 4 4 9 5 9 8 7 71 1 1 1 3 9 1 1 2 9 5 9]';
A=[7 6 4 6 4 6 4 7 4 7 7 79 2 3 9 3 4 9 5 9 8 5 83 9 9 5 9 8 2 9 2 4 9 41 1 1 1 1 9 1 1 1 9 1 9]';
mask = all(bsxfun(@ne,A,permute(B,[1 3 2])),3);
At = A.'; %//'
out = reshape(At(mask.'),[],size(A,1))
- 再看下面这个:对比 bsxfun 与 repmat 运行效率:
n = 300;
k = 1; % Change to 100 for the second graph
a = ones(10,1);
rr = zeros(n,1);
bb = zeros(n,1);
ntt = 100;
tt = zeros(ntt,1);for i = 1:nr = rand(1, i * k);% Timing bsxfunfor it = 1:ntttic;x = bsxfun(@plus, a, r);tt(it) = toc;endbb(i) = median(tt);% Timing repmatfor it = 1:ntttic;y = repmat(a, 1, i * k) + repmat(r, 10, 1);tt(it) = toc;endrr(i) = median(tt);
endfigure;
plot(1:n, bb, 'b', 'DisplayName', 'bsxfun');
hold on;
plot(1:n, rr, 'r', 'DisplayName', 'repmat');
legend('bsxfun','repmat')
运行时间对比结果:

可见对于大矩阵操作 bsxfun 效率更高!
So, 当你的矩阵规模比较大时,想想能否用 bsxfun 代替 repmat 吧!
相关文章:

Matlab arrayfun 与 bsxfun——提高编程效率的利器!
许多人知道 MATLAB 向量化编程,少用 for 循环 可以提高代码运行效率,但关于代码紧凑化编程, arrayfun 与 bsxfun 两个重要函数却鲜有人能够用好,今天针对这两个函数举例说明其威力。 Matlab arrayfun 概述 arrayfun 是 Matlab …...
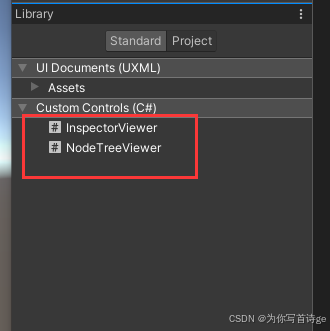
【Unity编辑器拓展】GraphView自定义可视化节点
1、创建节点区域脚本 其中的new class UxmlFactory,可以让该元素显示在UI Builder中,我们就可以在Library-Project中看到我们新建的这两个UI元素,就可以拖入我们的UI窗口编辑了 public class NodeTreeViewer : GraphView {public new class…...
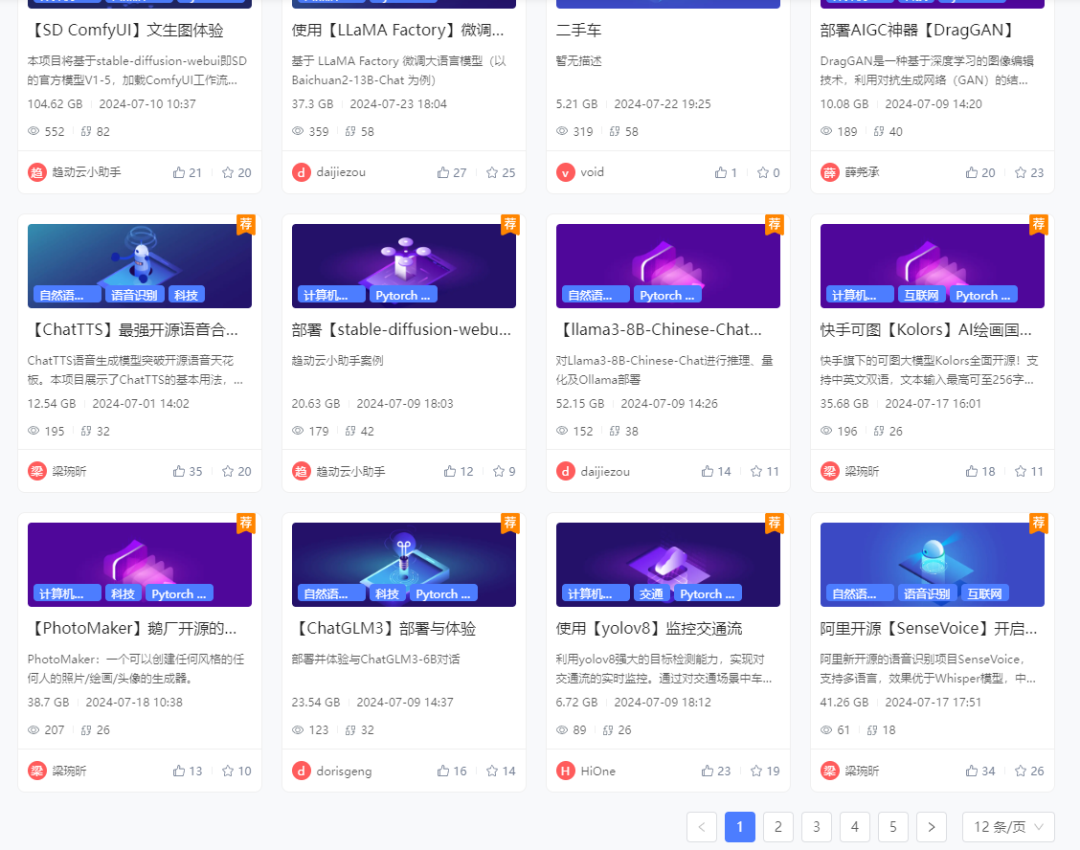
教程系列4 | 趋动云『社区项目』极速体验 LivePortrait 人脸表情“移花接木”大法
LivePortrait LivePortrait 由快手可灵大模型团队开源,只需 1 张原图就能生成动态视频。 LivePortrait 的核心优势在于其卓越的表情"迁移"技术,能够令静态图像中的人物瞬间焕发活力,无论是眨眼、微笑还是转头,皆栩栩如…...

WGS84、GCJ-02、BD09三大坐标系详解
文章目录 前言WGS84坐标系定义应用WGS84 Web 墨卡托投影 GCJ-02坐标系(火星坐标系)定义应用GCJ-02经纬度投影与Web墨卡托投影 BD09坐标系(百度坐标系)定义应用BD09经纬度投影与Web墨卡托投影 坐标系之间的区别与注意事项总结 前言…...

css上下动画 和淡化
.popup_hidden_bg { transition: opacity .5s ease-out; opacity: 0; pointer-events: none; /* 防止在隐藏时仍然能点击 */ } keyframes popupShop { from { transform: translateY(100%); opacity: 0; } to {transform: translateY(0);opacity: 1; }} keyframes popupHidd…...

深入解析C#中的URI和URL编码:理解EscapeDataString、EscapeUriString和UrlEncode的区别及字符编码错误处理
在C#中,处理URI(统一资源标识符)和URL(统一资源定位符)时,可以使用Uri.EscapeDataString、Uri.EscapeUriString和HttpUtility.UrlEncode(或WebUtility.UrlEncode)方法来编码字符串。…...

【CSS】给图片设置 max-width
.logo img{width:100%; /* 缩成父盒子的100% */max-width:100%; /* (谁小用谁的百分之百) *//* max-width:100%;【1】图片比盒子大,缩成父盒子的100%【2】图片比盒子小,图片自身的100%*/ }示例 设置样式 .el-image {width: 100%;max-width: 100%;max-…...
)
区块链——代码格式检查(prettier、solhint)
一、引入依赖 // 导入prettier prettier-plugin-solidity yarn add --dev prettier prettier-plugin-solidity yarn add --dev solhint二、创建.prettierrc文件 {"tabWidth": 2,"semi": false,"useTabs": false,"singleQuote": fals…...
搭建自动化 Web 页面性能检测系统 —— 部署篇
作为一个前端想去做全栈的项目时,可能第一个思路是 node vue/react。一开始可能会新建多个工程目录去实现,假设分别为 web 和 server,也许还有管理后台的代码 admin,那么就有了三个工程的代码。此时为了方便管理就需要在远程仓库…...
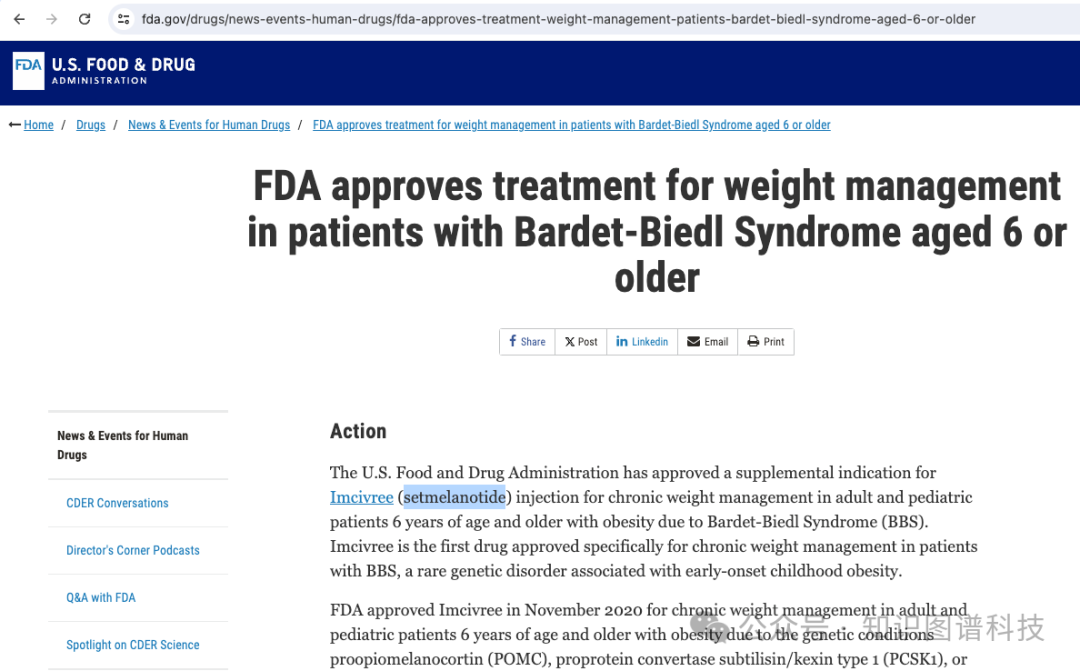
知识图谱增强的RAG(KG-RAG)详细解析
转自:知识图谱科技 这是一个与任务无关的框架,它将知识图谱(KG)的显性知识与大型语言模型(LLM)的隐含知识结合起来。这是该工作的arXiv预印本 https://arxiv.org/abs/2311.17330 。 我们在这里利用一个名为…...

python中list的深拷贝和浅拷贝
其实这还是涉及到python中的可变对象和不可变对象的概念。 https://www.cnblogs.com/poloyy/p/15073168.html # -*- coding: utf-8 -*-person [name, [savings, 100.00]] hubby person[:] # slice copy wifey list(person) # fac func copy a [id(x) for x in person] b …...

【LeetCode】字母异位词分组
题目描述: 给你一个字符串数组,请你将字母异位词组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”] 输出: [[“bat”…...

Golang | Leetcode Golang题解之第295题数据流的中位数
题目: 题解: type MedianFinder struct {nums *redblacktree.Treetotal intleft, right iterator }func Constructor() MedianFinder {return MedianFinder{nums: redblacktree.NewWithIntComparator()} }func (mf *MedianFinder) AddNum(…...

【C语言】C语言期末突击/考研--数据的输入输出
目录 一、printf()输出函数介绍 二、scanf读取标准输入 (一)scanf函数的原理 (二)多种数据类型混合输入 三、练习题 今天我们学习printf和scanf读取标准输入。下面我们开始正式的学习吧。 C语言中有很多内置函数,今…...

How can I fix my Flask server‘s 405 error that includes OpenAi api?
题意:解决包含OpenAI API的Flask服务器中出现的405错误(Method Not Allowed,即方法不允许) 问题背景: Im trying to add an API to my webpage and have never used any Flask server before, I have never used Java…...
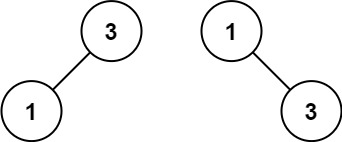
LeetCode Hot100 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确…...

【Linux】线程的控制
目录 线程等待 线程退出 线程的优缺点 线程独占和共享的数据 我们说Linux是用进程模拟的线程,所以Linux中只有轻量级进程的概念,但是,用户是只认线程的,所以我们有一个叫原生线程库的东西,它就负责把轻量级进程的系…...

Vue3自研开源Tree组件:人性化的拖拽API设计
针对Element Plus Tree组件拖拽功能API用的麻烦,小卷开发了一个API使用简单的JuanTree组件。拖拽功能用起来非常简单! 文章目录 使用示例allowDragallowDrop支持节点勾选支持dirty检测后台API交互 源码实现 使用示例 组件的使用很简单: 通过…...

MYSQL--触发器详解
触发器 1.触发器简介 触发器(trigger)是一个特殊的存储过程,它的执行不是由程序调用,也不是手工启动,而是由事件来触发,比如当对一个表进行操作( insert,delete, update…...

C++实用指南:Lambda 表达式的妙用
Lambda 表达式的灵活性和强大功能确实为编程提供了许多便利。但是我们发现许多开发者仍然无法灵活运用其便利,于是写了这篇文章。 Lambda 允许我们编写更简洁和灵活的代码。例如在处理网络请求时,我们经常需要确保响应与当前的状态或需求仍然相关。通过…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
