机器学习数学基础(2)--最大似然函数
声明:本文章是根据网上资料,加上自己整理和理解而成,仅为记录自己学习的点点滴滴。可能有错误,欢迎大家指正。
在机器学习和统计学领域中,似然函数(Likelihood Function)是一个至关重要的概念。它不仅是参数估计的基础,而且在模型选择、模型评估以及众多先进的算法和技术中都有着广泛的应用。
1. 似然VS概率
概率和似然是统计学中两个不同的概念,它们在概念上和应用上都有所区别。以下是通过一个具体例子来展示这两者之间的区别:
1.1 概率(Probability)
定义:概率是在给定的参数下,某个事件发生的可能性。它是未来事件发生的度量,通常用介于0和1之间的数值表示。
例子:假设我们有一个标准的六面骰子,每个面上有1到6的数字。当我们掷骰子时,得到数字6的概率是:𝑃(数字=6)=1/6
在这个例子中,参数是骰子的面数(6面),事件是掷出数字6,概率是已知的,并且是在掷骰子之前就确定的。这里的关键是,概率是在给定参数(骰子的公平性,即所有面出现概率相同)的情况下,事件发生的可能性。
1.2 似然(Likelihood)
定义:似然是在已知观测数据的情况下,这些数据对于不同参数值的支持程度。它不是数据发生的概率,而是在给定数据时参数值的相对合理性。
现在,假设我们不确定骰子是否公平,我们通过掷骰子20次,观察到数字6出现了5次。我们想要估计掷出数字6的真实概率 𝜃:
- 似然函数 表示为 𝐿(𝜃∣5次6),是 𝜃 的函数,表示在参数 𝜃下观测数据(5次6)的相对可能性。似然函数是: 𝐿(𝜃∣5次6)=
。
- 对𝜃的求解,可用最大似然方法,具体可看后面,这时求出的𝜃的值不一定是1/6。
对比上面的例子:
概率函数 给出了在给定参数下事件发生的可能性。在我们的例子中,它告诉我们在假设骰子公平的情况下,掷出6的概率是 1/6。
似然函数 用于在已知观测数据的情况下,评估不同参数值的合理性。在我们的例子中,它帮助我们根据观测到的5次6来估计 𝜃 的值。
1.3 两者区别:
- 概率是已知参数下事件的度量:在概率中,参数是已知的,我们计算的是某个事件发生的可能性。
- 似然是已知数据下参数的度量:在似然中,数据是已知的,我们评估的是不同参数值对数据的支持程度。
- 概率是绝对的:概率给出了在给定参数下事件发生的确切概率。
- 似然是相对的:似然比较了在已知数据下,不同参数值的相对合理性。
总结来说,概率关注的是在给定参数下事件发生的可能性,而似然关注的是在给定数据下参数值的合理性。这两者在统计分析中扮演着不同的角色。
2. 概率函数VS似然函数
2.1 概率函数(Probability Function, PF)
-
定义:概率函数是描述随机变量取各种可能值的概率。对于离散随机变量,它是一个定义在所有可能结果上的函数;对于连续随机变量,它是一个概率密度函数。
-
用途:概率函数用于计算在给定参数下,随机变量取特定值或处于某个区间的概率。
(1)概率函数
- 对于离散型随机变量,概率函数通常指的是概率质量函数(Probability Mass Function, PMF),它给出了随机变量取每个可能值的概率.
-
对于离散随机变量 X,概率函数可以表示为
,满足以下性质:。
- 非负性:对于所有的 𝑥x,有 𝑃(𝑋=𝑥)≥0。
- 归一性:所有可能的 𝑥x 上的概率之和为1,即:
- 对于连续随机变量 X
(2) 概率密度函数(Probability Density Function, PDF)
- 概率密度函数是用于描述连续型随机变量在某个值或某个区间内取值的概率的函数。
- 对于连续型随机变量 X,其概率密度函数
表示为
,其中
是累积分布函数满足以下性质:
- 非负性:对于所有的 𝑥,有 𝑓(𝑥)≥0。
- 归一性:𝑋的整个取值范围内,概率密度函数的积分总和为1,即:
2.2 似然函数(Likelihood Function, LF)
-
定义:似然函数是在已知观测数据的情况下,这些数据对于不同参数值的相对可能性。它是参数的函数,用于估计参数。
-
用途:似然函数用于参数估计,特别是在最大似然估计中,通过找到使似然函数最大化的参数值。
-
数学表示:对于简单随机样本,似然函数可以表示为观测数据的概率函数的乘积:
其中,𝜃 是参数,
是观测值,
是给定参数 𝜃下第 𝑖个观测值的概率密度函数或概率质量函数。
2.3 两者区别:
- 参数与数据的角色:在概率函数中,参数是已知的,数据是随机的;而在似然函数中,数据是已知的,参数是未知的。
- 目的:概率函数用于计算特定事件发生的概率,似然函数用于估计模型参数。
- 形式:概率函数通常与特定的概率分布相关联(如正态分布、二项分布等),而似然函数是观测数据对参数的函数。
例子:假设我们有一个骰子,并且想知道掷出6点的概率 𝜃。
- 概率函数:如果我们假设骰子是公平的,那么掷出6点的概率函数是 𝑃(6点)=𝜃=1/6。
- 似然函数:若我们掷了20次,观察到5次6点,似然函数将是
。我们通过最大化这个似然函数来估计 𝜃 的值。
3.最大似然估计
极大似然估计(Maximum Likelihood Estimation, MLE)是一种在已知观测数据的情况下估计概率模型参数的方法。它基于以下原则:
-
似然函数:首先定义似然函数,它是在给定参数值
下观测数据
的概率。对于独立同分布的观测数据
,似然函数可以表示为所有观测数据
的概率密度函数(对于连续型随机变量)或概率质量函数(对于离散型随机变量)的乘积:
-
最大化似然:然后,选择使似然函数达到最大值的参数
。这些参数值被称为极大似然估计值。
-
对数转换:为了简化计算,通常对似然函数取对数,因为对数是单调函数,可以将乘积转换为求和:
-
求解参数:对对数似然函数求导,并找到导数为零的点,这通常涉及到数值优化技术。
-
统计性质:在大样本情况下,极大似然估计具有一些良好的统计性质,如一致性(估计值随着样本量的增加而趋近于真实值)和渐近正态性(估计量的分布趋近于正态分布)。
仍然是上面的例子:现在,假设我们不确定骰子是否公平,我们通过掷骰子20次,观察到数字6出现了5次。我们想要估计掷出数字6的真实概率 𝜃:
写出似然函数:根据观测结果(例如,掷20次得到5次6),写出似然函数:
取对数:为了简化计算,通常对似然函数取对数,得到对数似然函数:
求导数:对 𝜃 求导,并找到导数为零的点,这通常通过设置导数等于零并解方程来完成:
解方程:解上述导数等于零的方程,得到 𝜃 的值:
,可得
得到最大似然估计:解得
或 0.25,这就是掷出数字6的最大似然估计概率。
如果骰子是完全公平的,我们期望 θ 接近 1/6,但由于我们的样本数据,我们得到的估计值是 1/4。这可能表明骰子存在偏差,或者仅仅是由于随机变异。
4. 似然比
似然比(Likelihood Ratio)是统计学中用于比较两个统计模型对同一数据集的拟合优度的量。它是两个似然函数值的比率,通常用于模型选择、假设检验和参数估计中。
定义:
似然比 𝜆λ 可以定义为两个模型的似然函数值的比值: 其中,
和
分别是参数 𝜃1和 𝜃2 下观测数据 𝑋 的似然函数值。
应用:
- 模型选择:在比较两个模型时,似然比可以用来评估哪个模型对数据的拟合更好。
- 似然比检验:一种统计假设检验方法,用于比较零假设(𝐻0H)和备择假设(𝐻1)下的似然函数值。
例子:假设我们有一个简单的数据集,由10个观测值组成,我们想要比较以下两个模型:
- 模型1(零假设 𝐻0): 假设观测值来自均值为
,标准差为
的正态分布。
- 模型2(备择假设 𝐻1): 假设观测值来自均值为
,标准差为
的正态分布。
假设我们观测到的数据是 X={2,3,4,5,6,7,8,9,10,11}。
计算似然函数:首先,我们为每个模型计算似然函数。假设
和
是已知的,我们只估计均值 𝜇。
模型1的似然函数(假设
):

模型2的似然函数(假设
):
计算似然比:
评估似然比:如果似然比 𝜆 接近1,说明两个模型对数据的拟合程度相似;如果 𝜆 显著大于1,模型1可能更合适;如果 𝜆显著小于1,模型2可能更合适。
似然比检验:在实际应用中,我们通常对数化似然比,并将其与特定的统计量进行比较,以决定是否拒绝零假设。
通过这个例子,我们可以看到似然比如何用于比较不同模型对同一数据集的拟合优度,并在模型选择和假设检验中发挥作用。
相关文章:
机器学习数学基础(2)--最大似然函数
声明:本文章是根据网上资料,加上自己整理和理解而成,仅为记录自己学习的点点滴滴。可能有错误,欢迎大家指正。 在机器学习和统计学领域中,似然函数(Likelihood Function)是一个至关重要的概念。…...

详解 @RequestHeader 注解在 Spring Boot 中的使用
个人名片 🎓作者简介:java领域优质创作者 🌐个人主页:码农阿豪 📞工作室:新空间代码工作室(提供各种软件服务) 💌个人邮箱:[2435024119@qq.com] 📱个人微信:15279484656 🌐个人导航网站:www.forff.top 💡座右铭:总有人要赢。为什么不能是我呢? 专栏导…...

C# 表达式树的简介与说明
文章目录 1. 表达式树是什么?2. 表达式树的基本组成3. 构建表达式树的步骤4. 表达式树的使用场景5. 示例代码6. 总结 在 C# 编程中,表达式树(Expression Tree)是一个强大的概念,它允许我们以代码的形式表示运行时的代码…...
【北京迅为】《i.MX8MM嵌入式Linux开发指南》-第三篇 嵌入式Linux驱动开发篇-第六十三章 输入子系统实验
i.MX8MM处理器采用了先进的14LPCFinFET工艺,提供更快的速度和更高的电源效率;四核Cortex-A53,单核Cortex-M4,多达五个内核 ,主频高达1.8GHz,2G DDR4内存、8G EMMC存储。千兆工业级以太网、MIPI-DSI、USB HOST、WIFI/BT…...

[补题记录]Leetcode 15. 三数之和
传送门:三数之和 思路 为了去重,需要先排序。 排序之后,显然每一个 n u m s [ i ] nums[i] nums[i] 就可以作为三数之中的第一个数。 因此,对于每一个 i i i,第二、三个数只能在 [ i 1 , n ] [i 1, n] [i1,n]…...

什么是sql注入攻击,如何预防介绍一下mysql中的常见数据类型
什么是sql注入攻击,如何预防 sql注入攻击指的是应用程序对用户输入数据的合法性没有判断或者过滤不严格,在sql语句中插入任意的恶意语句进行非法操作。 预防方式1:使用预编译语句比如PrepareStatement,用户输入的所有数据都以参数…...

史上最全的Seata教学并且连接springcloudAlibaba进行使用
来都来了点个赞收藏一下在走呗~~🌹🌹玫瑰 一、Seata是什么 Seata(Simple Extensible Autonomous Transaction Architecture,简单可扩展自治事务框架)是一种分布式事务解决方案,旨在解决分布式系统中的事务…...
InternLM Git 基础知识
提交一份自我介绍。 创建并提交一个项目。...

【Unity模型】古代亚洲建筑
在Unity Asset Store上,一款名为"Ancient Asian Buildings Pack"(古代亚洲建筑包)的3D模型资源包,为广大开发者和设计师提供了一个将古代亚洲建筑风格融入Unity项目的机会。本文将详细介绍这款资源包的特点、使用方式以…...

木马后门实验
实验拓扑 实验步骤 防火墙 配置防火墙—充当边界NAT路由器 边界防火墙实现内部 DHCP 分配和边界NAT需求,其配置如下 登录网页 编辑接口 配置e0/0 配置e0/1 编辑策略 测试:内部主机能获得IP,且能与外部kali通信 kali 接下来开启 kali 虚…...

【React】useState:状态更新规则详解
文章目录 一、基本用法二、直接修改状态 vs 使用 setState 更新状态三、对象状态的更新四、深层次对象的更新五、函数式更新六、优化性能的建议 在 React 中,useState 是一个非常重要的 Hook,用于在函数组件中添加状态管理功能。正确理解和使用 useState…...

C#中的异步编程:Task、Await 和 Async
public async void DoSth() {await Task.Run(() > {//...DoSth...}); } ①函数的返回类型前加上: async ②函数内加上: await Task.Run(() > { }); ③在上面{ ... } 内添加要处理的程序代码, 这样运行到 DoSth() 函数就…...
SSRF-labs-master靶场
目录 file_get_content.php sql_connect.php download.php dns-spoofing.php dns_rebinding.php 访问链接 http://127.0.0.1/SSRF/# file_get_content.php 在编程语言中,有一些函数可以获取本地保存文件的内容。这些功能可能能够从远程URL以及本地文件 如果没…...

HBuilder X中配置vue-cli项目和UI库
目录 一.前端项目结构 二.在HBuilder X中搭建vue-cli项目 1. 安装node.js前端环境 2. HBuilder X创建一个vue-cli项目 3. vue-cli项目结构 4. 如何运行前端项目 5. 创建组件 6. 组件路由(页面跳转) 6.1 创建router目录 6.2 使用路由 6.3 在main.js中配置路由 6.4 路…...
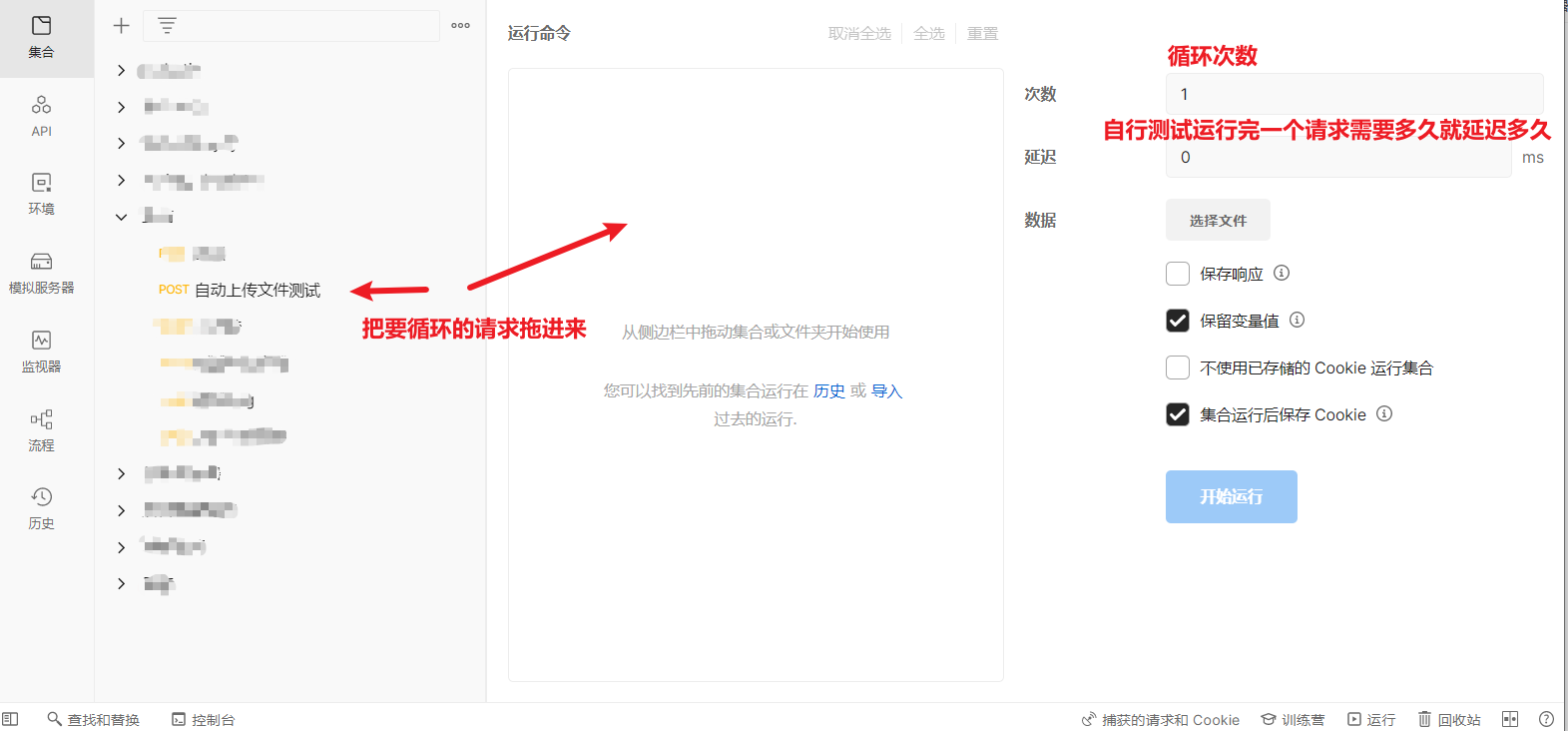
如何用PostMan按照规律进行循环访问接口
①设置动态变量 步骤一: 设置环境变量 1. 创建环境变量集合 在 Postman 左上角选择 "环境",然后点击 "添加" 来创建一个新的环境变量集合。给它起一个名称,比如 "uploadDemo". 2. 添加初始变量 在新创建的环境变量集…...
稳态准直太阳光模拟器仪器光伏电池组件IV测试
太阳能模拟器电池IV测试仪、单体测试仪,配备匹配标准的AAA Class稳态太阳能模拟器及相关测试附件,可对太阳能电池片的IV性能进行测量、分级分选等; 介绍 AAA class太阳光模拟器整合完整的IV测量系统,针对各种太阳能电池的性能&a…...
-代理Set和Map及ref原理)
vue3 reactive原理(二)-代理Set和Map及ref原理
Set和Map类型的数据也属于异质对象,它们有特定的属性和方法用来操作自身。因此创建代理时,针对特殊的方法需要特殊的对待。 Vue 的ref 是基于reactive函数实现的,它在其基础上,增加了基本类型的响应性、解决reactive在解构时丢失…...

Python自然语言处理库之NLTK与spaCy使用详解
概要 自然语言处理(NLP)是人工智能和数据科学领域的重要分支,致力于让计算机理解、解释和生成人类语言。在Python中,NLTK(Natural Language Toolkit)和spaCy是两个广泛使用的NLP库。本文将详细介绍NLTK和spaCy的特点、功能及其使用方法,并通过具体示例展示如何使用这两…...

Hive-内部表和外部表
区别 内部表实例 准备数据 查看数据 删除数据 外部表实例 准备数据 查看数据 删除数据 区别 内部表:管理元数据(记录数据的文件和目录的信息)和数据。当删除内部表时,会删除数据和表的元数据,所以当多个表关…...
)
Java并发编程(三)
Java并发编程 1、什么是 Executors 框架 Executors框架是一个根据一组执行策略调用,调度,执行和控制的异步任务的框架。 无限制的创建线程会引起应用程序内存溢出。所以创建一个线程池是个更好的的解决方案,因为可以限制线程的数量并且可以…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
