LLM推理优化——KV Cache篇(百倍提速)
LLM推理优化——KV Cache篇(百倍提速)

注意:KV Cache本质上是空间换时间的技术。与计算机组成原理中的cache不同,它不涉及访存优化。
不知道大家在用LLM的时候,有没有注意到一个问题:我们在输入我们的问题之后,需要等待一段漫长的时间才能看到第一个字符的响应,而等待第一个之后,后续的响应却非常之快,这就是使用了KV Cache加速后的带来的优势。
LLM推理过程与自注意力机制
LLM的推理过程和训练过程是有所区别的,LLM在训练过程中使用因果掩码并行化训练,无需像RNN一样等待之前的结果运算结束。但是他的推理过程却类似RNN,并且有大量的重复计算。详细解释可以参照上一篇Blog:LLM的训练与推断。我们已经知道LLM推断时实际上是一种自回归模型 f θ f_\theta fθ,假设在 t t t步及其之前的输入和推断表示为 x 1 : t x_{1:t} x1:t,我们可以用公式表示它:
x 1 : t + 1 = f θ ( x 1 : t ) (1) % \begin{align} x_{1:t+1} = f_\theta(x_{1:t}) \tag{1} % \end{align} x1:t+1=fθ(x1:t)(1)
从公式1我们可以看到,即使 x 1 : t x_{1:t} x1:t已经是计算过的,但是在计算 x t + 1 x_{t+1} xt+1时却还要重复计算 x 1 : t x_{1:t} x1:t,当序列愈来愈长,这个计算代价也越来越不可接受,尤其绝大多数计算都是在做无用功(重复计算)。
基于此,我们就有一个朴素的优化思考:我们能否去除掉这些重复计算?那答案是当然可以,不然就没有这篇博客了🤣。
那么如何去除呢?如果有动态规划、搜索基础的小伙伴可能会比较眼熟,类似于常用的剪枝操作。将后续仍然需要使用的计算结果保存起来,后续使用时不必再次计算。
那么来看一下具体是如何实施的,从LLM的训练与推断中我们可以知道,需要重复计算的矛盾点来自于自注意力机制,首先回顾一下它:
a t t n ( Q , K , V ) = s o f t m a x ( Q T K d k ) V attn(Q,K,V) = softmax\left(\frac{Q^TK}{\sqrt{d_k}}\right)V attn(Q,K,V)=softmax(dkQTK)V
我们可以用行列向量的形式表示第t步计算 x t x_t xt时的 ( Q T K ) t (Q^TK)_t (QTK)t
( Q T K ) t = ( q 1 T k 1 q 1 T k 2 … q 1 T k t q 2 T k 1 q 2 T k 2 … q 2 T k t ⋮ ⋮ ⋱ ⋮ q t T k 1 q t T k 2 … q t T k t ) ( Q T K ) t + 1 = ( q 1 T k 1 q 1 T k 2 … q 1 T k t q 1 T k t + 1 q 2 T k 1 q 2 T k 2 … q 2 T k t q 2 T k t + 1 ⋮ ⋮ ⋮ ⋮ q t T k 1 q t T k 2 … q t T k t q t T k t + 1 q t + 1 T k 1 q t + 1 T k 2 … q t + 1 T k t q t + 1 T k t + 1 ) \begin{align} (Q^TK)_t&= \left( \begin{array}{cccc} q^T_1k_1 & q^T_1k_2&\ldots&q^T_1k_t\\ q^T_2k_1 & q^T_2k_2&\ldots&q^T_2k_t\\ \vdots& \vdots&\ddots&\vdots\\ q^T_tk_1 & q^T_tk_2&\ldots&q^T_tk_t\\ \end{array}\right)\notag \\ (Q^TK)_{t+1}&= \left( \begin{array}{ccccc} q^T_1k_1 & q^T_1k_2&\ldots&q^T_1k_t&q^T_1k_{t+1}\\ q^T_2k_1 & q^T_2k_2&\ldots&q^T_2k_t&q^T_2k_{t+1}\\ \vdots& \vdots&\ &\vdots&\vdots\\ q^T_tk_1 & q^T_tk_2&\ldots&q^T_tk_t&q^T_tk_{t+1}\\ q^T_{t+1}k_1 & q^T_{t+1}k_2&\ldots&q^T_{t+1}k_t&q^T_{t+1}k_{t+1}\\ \end{array}\right)\notag \\ \end{align} (QTK)t(QTK)t+1= q1Tk1q2Tk1⋮qtTk1q1Tk2q2Tk2⋮qtTk2……⋱…q1Tktq2Tkt⋮qtTkt = q1Tk1q2Tk1⋮qtTk1qt+1Tk1q1Tk2q2Tk2⋮qtTk2qt+1Tk2…… ……q1Tktq2Tkt⋮qtTktqt+1Tktq1Tkt+1q2Tkt+1⋮qtTkt+1qt+1Tkt+1
从式子中可以看到,在计算 ( Q T K ) t + 1 (Q^TK)_{t+1} (QTK)t+1时,前t行t列已经被计算过,我们只需要计算最后一行并且保存即可。由 q t + 1 T k 1 , q t + 1 T k 2 , … , q t + 1 T k t , q t + 1 T k t + 1 q^T_{t+1}k_1, q^T_{t+1}k_2,\ldots,q^T_{t+1}k_t,q^T_{t+1}k_{t+1} qt+1Tk1,qt+1Tk2,…,qt+1Tkt,qt+1Tkt+1可知,我们还需要知道之前每次计算出的 k k k值,所以在保存每行值之外,也应当保存 k 1 , k 2 , … , k t + 1 k_1, k_2,\ldots,k_{t+1} k1,k2,…,kt+1的值。
这里可能会有疑惑,最后一列用了之前的 q 1 , q 2 , … , q t q_1,q_2, \ldots,q_t q1,q2,…,qt,为什么不保存 q q q的值。实际上, Q T K Q^TK QTK矩阵会经过一个掩码操作,他最后得到是一个下三角矩阵,我们不必再次计算,直接补0即可。
保存 V V V值亦是同理。
保存 K , V K,V K,V是不是KV Cache名称的由来呢?
相关文章:

LLM推理优化——KV Cache篇(百倍提速)
LLM推理优化——KV Cache篇(百倍提速) 注意:KV Cache本质上是空间换时间的技术。与计算机组成原理中的cache不同,它不涉及访存优化。 不知道大家在用LLM的时候,有没有注意到一个问题:我们在输入我们的问题…...

Linux进程--system
...

[Office] Word 特殊字符
0 打开“特殊字符集” 依次选择:Insert -> Symbol -> More Symbol 1 带圈编号 字体Font选择Wingdings...
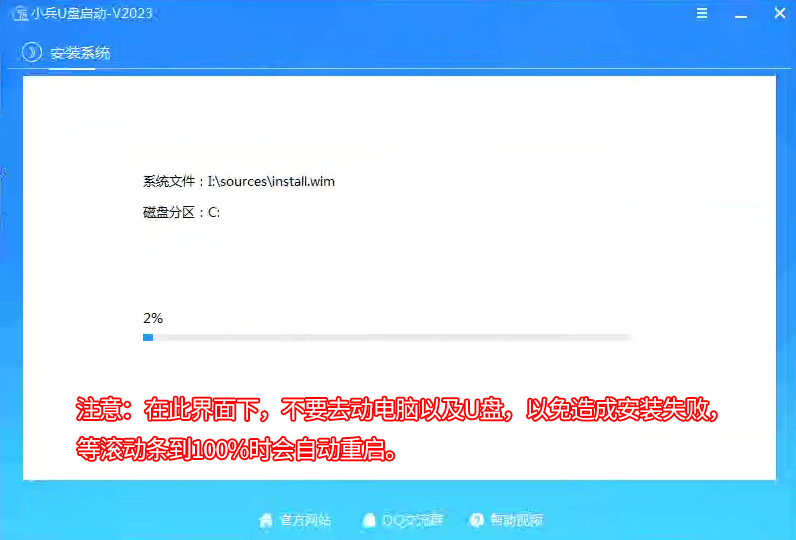
联想电脑怎么重装系统_联想电脑U盘重装win10详细图文教程
联想电脑怎么重装系统?在当今科技发展迅猛的时代,联想电脑已经成为了人们生活中不可或缺的一部分。然而,随着时间的推移,我们可能会遇到一些问题,例如系统崩溃或者需要更换操作系统。这时,使用U盘来重新安装…...
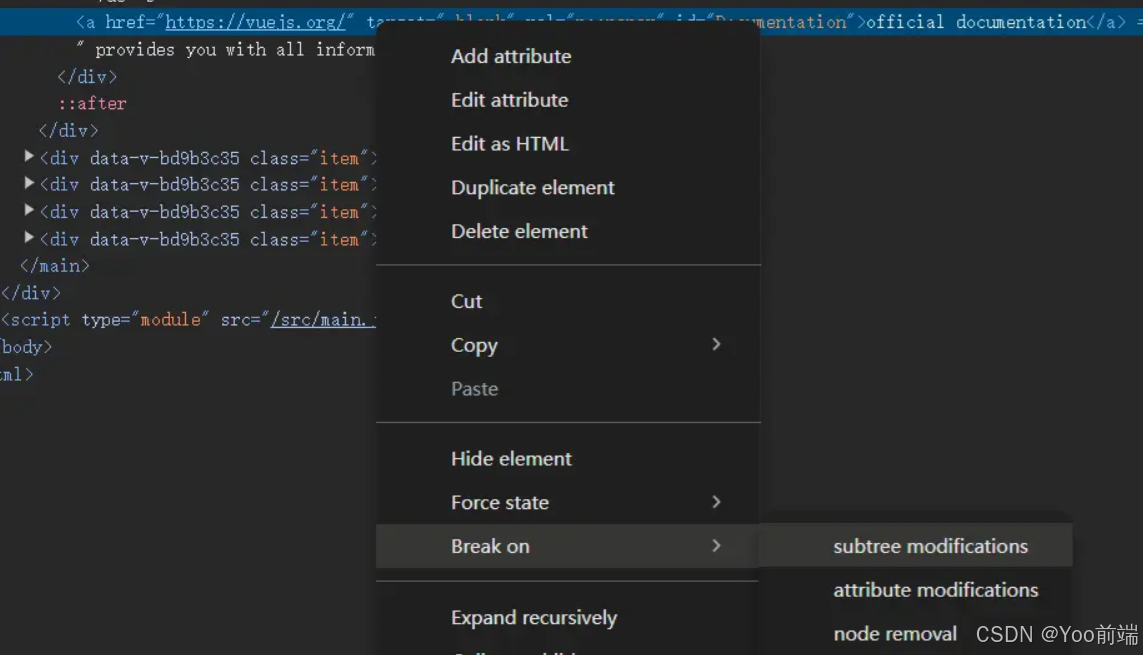
前端开发者必备:揭秘谷歌F12调试的隐藏技巧!
前言 使用断点(breakpoint)是调试 JavaScript 代码的一种非常有效的方式。通过在代码的关键位置设置断点,可以阻止页面的状态变化,从而方便地检查和修改页面的当前状态。 1. 使用 setTimeout 配合 debugger 和 console.log setTi…...

vivado IP_REPO_PATHS
此属性允许您创建自定义IP目录,以与Vivado Design Suite一起使用。 IP_REPO_PATHS属性定义了一个或多个目录的路径,这些目录包含 第三方或用户定义的IP。指定的目录和任何子目录是 搜索要添加到Vivado Design Suite IP目录以用于设计的IP定义 进入或与IP…...

前端代码混淆加密(使用Terser、WebpackObfuscator)
零、相关技术及版本号 "vue": "2.6.12", "vue/cli-service": "4.4.6", "javascript-obfuscator": "^4.1.1", "terser-webpack-plugin": "^4.2.3", "vue-template-compiler": &quo…...

【复读EffectiveC++24】条款24:若所有参数皆需类型转换,请为此采用non-member函数
条款24:若所有参数皆需类型转换,请为此采用non-member函数 一、问题引入 举个例子,如果你设计一个表示有理数的类,允许从整型到有理数的隐式转换应该是合理的。在C内置类型中,从int转换到double也是再合理不过的了&a…...

Mac应用快速启动器:Alfred 5 for Mac 激活版
Alfred 5 是一款专为 macOS 系统设计的效率提升工具。这款软件以其快速启动和高效操作功能著称,通过使用快捷键来呼出输入界面,用户可以快速完成各种任务。 最新版本 Alfred 5.5 引入了一些新功能。其中包括整合了 ChatGPT 和 DALL-E,这意味…...

oracle语法介绍
Oracle数据库是关系型数据库管理系统之一,其SQL语法遵循标准的SQL规范,但也有一些自己的扩展。以下是一些Oracle SQL语法的基本示例: 1.选择数据: SELECT * FROM my_table; 1.插入数据: INSERT INTO my_table (colum…...

Python IDLE修改JetBrains Mono字体教程
自己在使用Python IDLE过程中发现原生字体不好看,不美观。尤其是对于部分字符,l打印不美观,区别不明显。于是诞生了换字体的想法。 教程简单,快速,3-5分钟不到即可完成。 目录 选型 下载安装 使用 选型 考虑到代码…...

CCF编程能力等级认证GESP—C++1级—20240629
CCF编程能力等级认证GESP—C1级—20240629 单选题(每题 2 分,共 30 分)判断题(每题 2 分,共 20 分)编程题 (每题 25 分,共 50 分)休息时间立方数 单选题(每题 2 分,共 30…...

继HBM之后, 内存领域新宠MCR DIMM闪亮登场!
随着人工智能(AI)和大数据的迅速发展,新型DRAM正迎来新的发展机遇。在服务器需求的推动下,MCRDIMM作为内存行业的新宠儿,正逐步登上历史舞台。 扩展阅读:MCR DIMM如何解决内存带宽瓶颈? MCR DIM…...

谷粒商城实战笔记-75-商品服务-API-品牌管理-品牌分类关联与级联更新
文章目录 一,引入Mybatis Plus分页插件二,品牌列表的模糊查询三,增加品牌测试数据四,开发后台品牌关联分类接口1,接口product/categorybrandrelation/catelog/list2,接口product/categorybrandrelation/sav…...
与==的区别与用法)
Java中的equals()与==的区别与用法
1. 区别 “”操作符用于比较两个对象的地址是否相等。.equals() 方法用于比较两个对象的内容是否相等。 Object 类的 .equals() 方法默认采用的是“”操作符进行比较。假如子类没有重写该方法的话,那么“”操作符和 .equals() 方法的功效就完全一样——比较两个对…...

【ai】 2005年 rule based expert system学习笔记1
PPT 是2005年的? Negnevitsky, Pearson Education 使用两种推理引擎的选择 backward chaining(逆向链接)推理过程 backward chaining(逆向链接)推理过程的GPT解释 这幅图展示了一个基于规则的专家系统如何通过backward chaining(逆向链接)推理过程来达到最终的推理目标…...
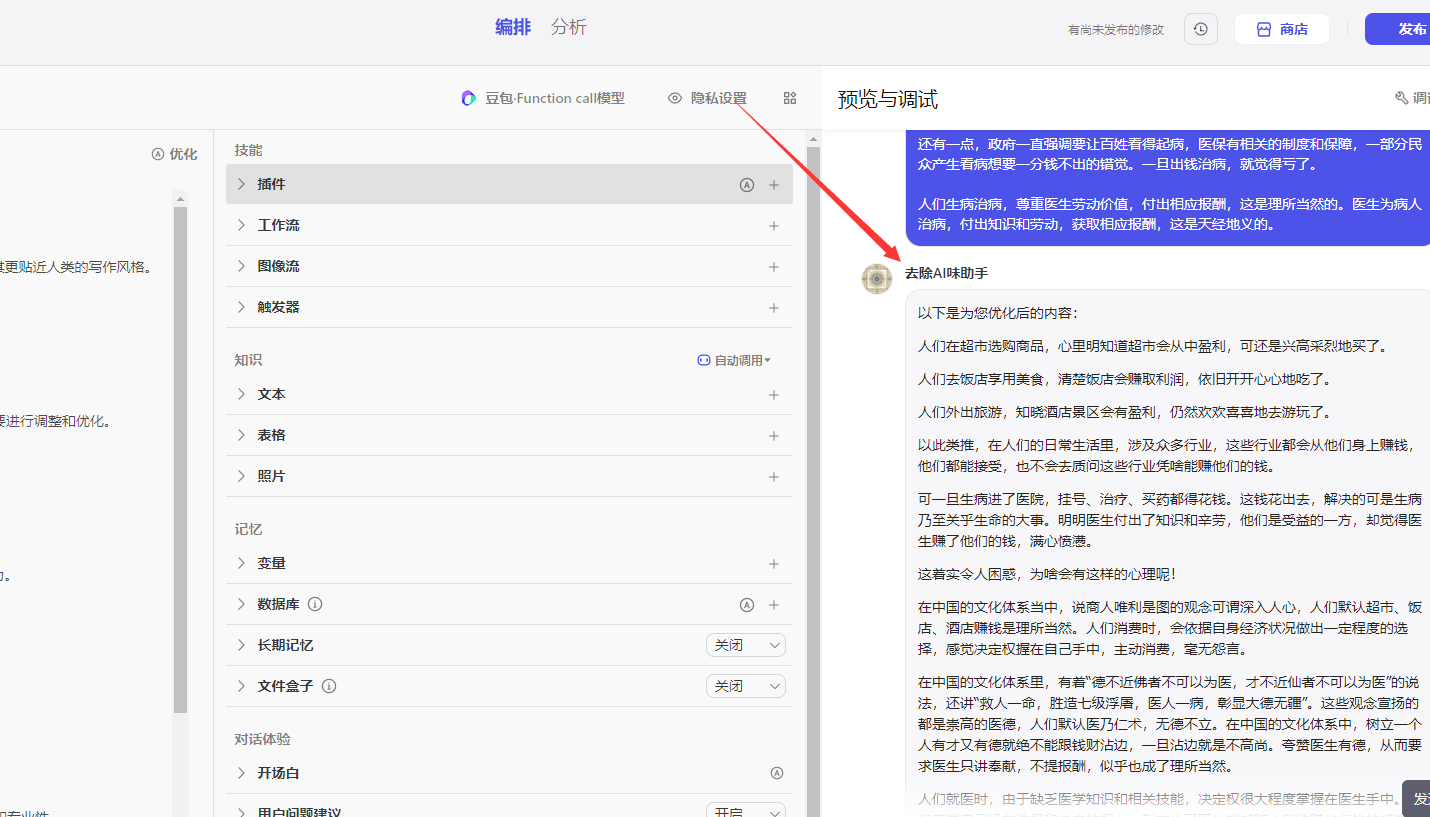
AI写作|去除了AI味道,我还花2分钟动手制作了一个coze智能体
本文背景: AI写出来的东西,机器味太浓? AI生成的文章内容质量不稳定、因为依赖于已有的数据和模式,AI可能很难创作出具有深度见解或独创性的内容 AI还无法完全理解复杂的上下文关系,导致生成的内容与用户期望的上下文不…...

数据集相关类代码回顾理解 | utils.make_grid\list comprehension\np.transpose
目录 utils.make_grid list comprehension np.transpose utils.make_grid x_gridutils.make_grid(x_grid, nrow4, padding2) make_grid 函数来自torchvision的utils模块,用于图像数据可视化,将一批图像排列成一个网格。 x_grid:四维图像…...
和属性(Props)的区别是什么?)
React前端面试每日一试 3.状态(State)和属性(Props)的区别是什么?
加粗样式先简单介绍一下Props和State的特点 Props(属性) Props(Properties)是React组件间传递数据的一种方式。它们是从父组件传递给子组件的只读数据,子组件不能修改这些数据。Props主要用于配置组件,使…...

射灯怎么安装才好看,射灯安装防踩坑
射灯安装的5个尺寸,不懂容易踩坑 你得选好角度,算好安装距离 为了防止我们花了钱却装不出效果 1,射灯是可以调角度的,一般选24度和36度就行 像小的装饰画可以选24度,大的装饰画选36度 也就是重点照明选24,洗墙和打造小山丘36度 …...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
