个人算法题精简导航整理(精炼汇总,含知识点、模板题、题单)
文章目录
- 前言
- 导航
- 注意事项
- 技巧类
- 自定义Pair
- 排序
- N维数组转一维
- 位运算
- 状态压缩
- 算法基础
- 枚举 √
- 指数型枚举
- 排列型枚举
- 组合型枚举
- 模拟 √
- 日期天数问题:平年闰年情况
- 递归&分治 √
- 贪心 √
- 货仓选址-模板题
- 排序 √
- 归并排序
- 前缀和&差分 √
- 前缀和
- 差分(一维、二维、三维)
- 二分 √
- 搜索
- DFS √
- BFS √
- IDA*
- 回溯
- 字符串
- KMP算法
- 动态规划 √
- 线性DP
- 背包DP
- 区间DP
- 树形DP
- 状态压缩DP
- 计数DP
- 数学 √
- 数论
- 算法基本定理
- 约数
- 最大公约数与公倍数
- 欧拉筛法(含朴素筛法、埃式筛法)
- 质数-欧拉筛
- 欧几里得与扩展欧几里得
- 辗转相除(含辗转相减法)
- 组合数学
- 容斥定理
- 快速幂
- 矩阵
- 数据结构
- 哈希表 √
- 树状数组 √
- 并查集
- 线段树 √
- 树上问题
- 树的直径
- 计算机几何
- 杂项
- 双指针 √
前言
本章节内容主要做一个全局算法题导航指引,含有代码基本模板、相对应习题以及相关知识点,所有题目围绕这个导航索引进行补充扩展,目前博主水平有限也在不断学习更新当前博客内容。
所有博客文件目录索引:博客目录索引(持续更新)
导航
OI Wiki:我愿称之为算法最全知识点合集!

对于Java的一些注意事项以及API可见:算法竞赛Java选手的语言快速熟悉指南
时间复杂度:
- n ∈ 1000:O(n2),dp
- n ∈ 10000:O(nlogn),二分、排序
- 210=1024,220=1048576(106),230=1073741824(109),240=1e12,250=1e15。【220约等于100万,231就爆一秒了】
- 10! = 362万,11! = 3900万,12! = 4亿,13! = 60亿
关于数据类型以及对应的内存范围:
- int:最大2147483647,20亿,2x1010
- long:占8个字节,64位,[-9223372036854775808到9223372036854775807] 百亿亿,9*219
- 1亿亿等于1兆,一百兆。
- 64MB:64MB最多可以开16777216个int
 ,相当于一千六百七十万个。
,相当于一千六百七十万个。
调试技巧:
①acwing官网问题
- 若是出现Segmentation fault,那么可以使用exit(0)来进行调试确定在哪一行出了错:
void func(){exit(0);
}//调用
func();
- 若是在func()放在当前行执行没有出现Segmentation fault,说明再此之前没有可能出现Segmentation fault,那么就可以将func放置到后面。
②关于输入输出
//输入、输出函数
static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
③自定义类及属性 > 定义一维数组效率。具体可见leetcode1235题
注意事项
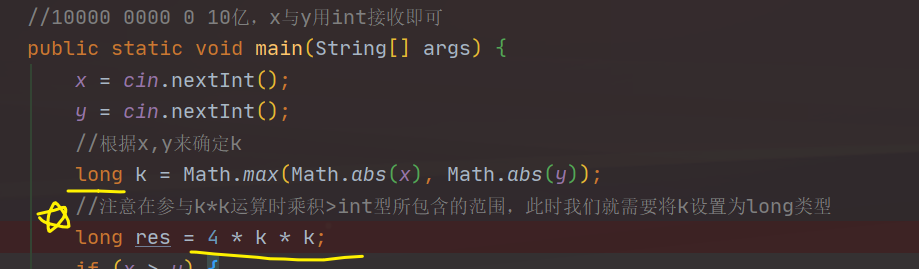
1、关于long res = 0; res = int * int出现精度问题
原因:int * int 得到的值会转为int类型,哪怕乘积是一个long类型,所以我们这边应该先将乘数先转为一个long类型才可。
案例1:1237. 螺旋折线,在java中对于这种k参与运算并且相乘结果超int范围的,必须将其本身也设置为long类型。
案例2:1814. 统计一个数组中好对子的数目

2、关于1e2问题
1e1就是10,若是有10个0,那么就是1e9情况。
技巧类
自定义Pair
自定义的键值对集合Pair:在acwing中需要自定义
static class Pair<K, V> {K x;V y;public Pair(K x, V y) {this.x = x;this.y = y;}
}
排序
①方式一:自定义类的话需要继承comparable接口,也就是实现compareTo方法
static class Node implements Comparable<Node> {public int ts;public int id;public Node(Integer ts, Integer id) {this.ts = ts;this.id = id;}public boolean equals(Node node) {return this.ts == node.ts && this.id == node.id;}@Overridepublic int compareTo(Node o) {if (this.ts == o.ts) return this.id - o.id;return this.ts - o.ts;}
}
②方式二:
//该接口是实现compare接口
Arrays.sort(list, (o1, o2)->{})
N维数组转一维
二维数组转一维:
int A, B;//A表示行数、B表示列数public int get(int i, int j) {return (i * B) + j;
}
三维数组转一维:
int A, B, C;public int get(int i, int j, int k) {return (i * B + j) * C + k;
}
位运算
与运算:
场景一:判断是偶数还是奇数
ch & 1 == 1 => 奇数 ch & 1 == 0 偶数
异或:
场景一:大写、小写字母转换,无需写if判断大小写来进行+32或-32,可直接进行ch ^= 1 << 5; 也就是异或32示例:https://leetcode.cn/problems/letter-case-permutation/
ch[i] ^= 1 << 5;//异或情况
a ^ b = c
a ^ c = b
状态压缩
5位状态:state = (1 << 5) - 1,此时即为11111
查看当前状态没有选择的:i = (1 << 5) - 1 - state
- 例如state=01100,最终i为10011。
当前状态补上新加的:state |= newState
- 例如state=00010,newState = 01100,最终结果为01110。
消除掉原先的一些状态:state = state & ~pack或者state ^ (state & pack),两个等价
- 例如state = 11111,消除目标pack = 01100,最终结果为10011。
算法基础
枚举 √
指数型枚举
模板题链接:92. 递归实现指数型枚举
题目:从 1∼n这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
复杂度分析:时间复杂度O(2n);空间复杂度O(n)
import java.util.*;class Main{private static int n;private static int[] arr;//0表示初始,1表示选,2表示不选public static void dfs(int u) {if (u == n) {//从选好的一组情况中来找到选的物品for (int i = 0; i < n; i++) {if (arr[i] == 1) {System.out.printf("%d ",i + 1);}}System.out.println();return;}//递归多种状态//选arr[u] = 1;dfs(u + 1);arr[u] = 0;//不选arr[u] = 2;dfs(u + 1);arr[u] = 0;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();arr = new int[n];dfs(0);}
}
排列型枚举
模板例题:94. 递归实现排列型枚举
示例:把 1∼n这n个整数排成一行后随机打乱顺序,输出所有可能的次序。
复杂度分析:时间复杂度为 O(n*n!);空间复杂度为O(n)
class Main {static int N = 9;static int n;//存储结果集private static int[] state = new int[N];//存储该路径是否访问过private static int[] vis = new int[N];//递归处理//dfs(0)开始public static void dfs (int u) {if (u == n) {//输出对应的方案for (int i = 0; i < n; i ++) {System.out.printf("%d", state[i]);}System.out.println();return;}//遍历枚举多种情况for (int i = 0; i < n; i ++) {if (!visited[i]) {visited[i] = true;state[u] = i + 1;//真实的值//递归dfs(u + 1);//恢复visited[i] = false;state[u] = 0;}}}}
组合型枚举
模板题目:93. 递归实现组合型枚举
介绍:在排列型中进行升级,原本给定3个数让你找到所有3个排列方案,而在这里有n个数,让你找对应m个( <= n)个数组合的排列情况。
复杂度分析:时间复杂度O(mn!)
class Main {static final int N = 15;static int n, m;//每个结果集都static int[] state = new int[N];public static void dfs(int u, int start) {//优化剪枝,提前结束if (u + (n - start) < m) return;//若是遍历的到终点个数个if (u == m) {//输出对应的方案for (int i = 0; i < n; i ++) {System.out.printf("%d ", state[i]);}System.out.println();}for (int i = start; i < n; i ++) {statue[u] = i + 1;dfs(u + 1, i + 1);statue[u] = 0;}}
}
模拟 √
日期天数问题:平年闰年情况
//平年28天,闰年为29天//判断闰年:不能被100整除,可以被4整除 或者 整除400
if (year % 100 != 0 && year % 4 == 0 || year % 400 == 0) static int[] months = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
//判断8位数是否是合法日期
public static boolean check(int d) {int year = d / 10000;int month = d % 10000 / 100;int day = d % 100;if (month > 12 || month == 0 || day > 31 || day == 0) return false;//闰年判断if (month != 2 && day > months[month]) return false;if (month == 2) {int leap = year % 4 == 0 && year % 100 != 0 || year % 400 == 0 ? 1 : 0;if (day > 28 + leap) return false;}return true;
}//判断日期的合法功能函数
public static boolean check(int year, int month, int day) {if (month > 12 || month == 0 || day > 31 || day == 0) return false;//闰年判断if (month != 2 && day > months[month]) return false;if (month == 2) {int leap = year % 4 == 0 && year % 100 != 0 || year % 400 == 0 ? 1 : 0;if (day > 28 + leap) return false;}return true;
}
日期时间点问题:
求 HH:mm:ss//获取到h小时m分钟s秒的总共秒数
public static int get_seconds(int h, int m, int s) {return h * 3600 + m * 60 + s;
} //将对应的总秒数去换算得到小时,分钟,秒数
int hour = time / 3600, minute = time % 3600 / 60, second = time % 60;
递归&分治 √
贪心 √
货仓选址-模板题
给你多个点,让你去确定在那个地点建仓库可以让来回距离最短:
将所有水平点存储到数组中对其进行排序,接着mid = (n + 1) / 2即可确定中间点,最后就是来进行求取距离。
- 若是有对应的公式推导成最终这个样子:|A1 - B| + |A2 - B| + |A3 - B| … + |An - B|,那么最后就是
ans += Math.abs(A[i] - A[mid])。
排序 √
归并排序
前缀和&差分 √
前缀和
一维前缀和:
s[i] = s[i - 1] + nums[i]
# 推导,其中nums的值需要从坐标1开始,若是默认给的从0开始则需要为s[i] = s[i - 1] + nums[i - 1]
s[1] = s[0] + nums[1]
s[2] = s[1] + nums[2] = nums[1] + nums[2]
s[3] = s[2] + nums[3] = nums[1] + nums[2] + nums[3]
# 计算范围:[1,3] s[3] - s[1 - 1] => [i, j] s[i] - s[j - 1]
二维前缀和:
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]# 计算范围 x1,y1 x2y2
sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]
差分(一维、二维、三维)
蓝桥杯三维差分题:AcWing 1232. 三体攻击
一维:
步骤一(反推b):b[i] = a[i] - a[i - 1]中间步骤(范围操作):
b[l] += c;
b[r + 1] -= c;步骤三:a[i] = a[i - 1] + b[i]
二维:
步骤一(反推b):b[i][j] = a[i][j] + a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1]中间步骤(范围操作):
b[x1][y1] += c
b[x2 + 1][y1] -= c
b[x1][y2 + 1] -= c
b[x2 + 1][y2 + 1] += c步骤三(反推a):a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j]
三维:
//步骤一:首先确定三维前缀和公式
b(x, y, z) = a(x, y, z) - a(x - 1, y, z) - a(x, y - 1, z) + a(x - 1, y - 1, z)- a(x, y, z - 1) + a(x - 1, y, z - 1) + a(x, y - 1, z - 1) - a(x - 1, y - 1, z - 1)中间步骤(范围操作):
二维正面(以z1为)
b[x1 ][y1 ][z1] += val
b[x1 ][y2 + 1][z1] -= val
b[x2 + 1][y1 ][z1] -= val
b[x2 + 1][y2 + 1][z1] += val
转为z2+1,且符号改变
b[x1 ][y1 ][z2 + 1] -= val
b[x1 ][y2 + 1][z2 + 1] += val
b[x2 + 1][y1 ][z2 + 1] += val
b[x2 + 1][y2 + 1][z2 + 1] -= val步骤三:最后反推求出a数组推导来进行计算
a(x, y, z) = b(x, y, z) + a(x - 1, y, z) + a(x, y - 1, z) - a(x - 1, y - 1, z)+ a(x, y, z - 1) - a(x - 1, y, z - 1) - a(x, y - 1, z - 1) + a(x - 1, y - 1, z - 1)
扩展:
1、前缀异或
相关题目:
- 第 314 场周赛—6201. 找出前缀异或的原始数组
二分 √
规律:一组单调递增或者递减情况(不限制于数字)情况时可以采用二分来进行优化。【O(n) -> O(logn)】
模板:
//第一类二分写法:check
int l = 0, r = n;
while (l < r) {int mid = l + r >> 1;if (mid >= target) l = mid + 1;else r = mid;
}int l = 0, r = n;
while (l < r) {int mid = (l + r + 1) >> 1;if (nums2[i] >= nums1[mid]) l = mid - 1;else r = mid;
}//第二种二分写法:
while (l != r) {int mid = l + ((r - l) >> 1);if (nums1[mid] < nums2[i]) l = mid + 1;else r = mid;
}
题单
蓝桥杯13届真题-求阶乘(算数基本定理、二分)
搜索
DFS √
题型:最大长度
模板:
void dfs(int step) //步长
{if(/*跳出循环的条件*/){return; //return十分关键,否则循环将会无法跳出}/*函数主体对功能进行实现*/for(/*对现有条件进行罗列*/){if(/*判断是否合理*/){//将条件修改dfs(/*新的step*/)/*!重中之重,当跳出那层循环后将数据全部归位*/} }
}
矩阵模板:
int f[4][2]={{0,1},{0,-1},{1,0},{-1,0}}; //用于判断下一步怎么走向几个方向走就是几个数据
void dfs(int x,int y){ //进入点的坐标if(/*跳出循环的条件*/){/*作出相应操作*/return; //不要忘了return}for(int i=0;i</*f的长度*/;i++){int x0=x+f[i][0]; /*此处是更新点的坐标,注意是直接让原来的点加上这个数据,不是直接等于*/int y0=y+f[i][1];if(/*用新坐标x0,y0判断是否符合条件*/){dfs(x0,y0); //用新的坐标进行递归}}
}
BFS √
题单
3、蓝桥杯13届真题-回忆迷宫(模拟、BFS)
模板
题型:最短路径。
模板:
1、二叉树:
class Solution {public static void main (String[] args) {Queue<TreeNode> queue = new LinkedList<>();queue.offer(xx);//添加root节点while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {//取出node结点进行操作TreeNode node = queue.poll();//放置左右子节点if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}res.add(1.0 * sum / size);}}
}
2、二维矩阵:
class Point {private int x;private int y;public Point(int x, int y) {this.x = x;this.y = y;}
}class Solution {public static void main (String[] args) {Queue<Point> queue = new LinkedList<>();queue.offer(new Point(1,2));//出发点while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {//取出Point结点进行操作Point point = queue.poll();//进行操作//放置四个方向的节点for (int d = 0; d < dicts.length; d++) {int x = point.x + dicts[d][0];int y = point.y + dicts[d][1];queue.offer(new Point(x, y))}}}}
}
3、坐标点写法:
class Solution {static final int N = 110;static int[] q = new int[N * N];static int hh, tt;//hh表示头指针(用于出队),tt表示入队指针//四个方向 (0, 1) (0, -1) (1, 0) (-1, 0)static int[] dx = {0, 0, 1, -1};static int[] dy = {1, -1, 0, 0};//矩阵static int[][] g = new int[N][N];static int H, W;//将二维坐标转为一个数字public static int get(int x, int y) {return x * (W + 1) + y;}public static void main (String[] args) {//bfs过程while (hh < tt) {int top = q[hh ++];int x = top / (W + 1);int y = top % (W + 1);//四个方向for (int k = 0; k < 4; k ++) {int xx = x + dx[k];int yy = y + dy[k];//搜索校验(边界情况 && 其他情况xxx)if (xx >= 1 && yy >= 1 && xx <= H && yy <= W) {//入队q[tt ++] = get(x, y);//相关动作xxx}}}}
}
IDA*
回溯
字符串
KMP算法
模板:
package com.changlu.string;public class KMP {public static void main(String[] args) {//APISystem.out.println("ababcabcaabbcdeabcdef".indexOf("abcaabb"));//手写System.out.println(kmp("ababcabcaabbcdeabcdef", "abcaabb"));}public static int kmp (String str, String sub) {int[] next = getNext(sub);for (int i = 0, j = 0; i < str.length(); i++) {while (j > 0 && str.charAt(i) != sub.charAt(j)) {j = next[j - 1];}if (str.charAt(i) == sub.charAt(j)) j++;//若是匹配到最后if (j == sub.length()) {return i - j + 1;}}return -1;}public static int[] getNext(String str) {int[] next = new int[str.length()];next[0] = 0;for (int i = 1, j = 0; i < str.length(); i ++) {while (j > 0 && str.charAt(i) != str.charAt(j)) {j = next[j - 1];}//若是当前字符相等if (str.charAt(i) == str.charAt(j)) {j++;}next[i] = j;}return next;}}
动态规划 √
线性DP
背包DP
区间DP
树形DP
状态压缩DP
计数DP
数学 √
数论
算法基本定理
知识点
算数基本定理
题单
蓝桥杯13届真题-求阶乘(算数基本定理、二分)
约数
约数个数及约数之和知识点(含公式)
最大公约数与公倍数
//最大公约数 greatest common divisor
int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);
}
//最小公倍数 Lowest Common Multiple
int lcm(int a, int b) {return a * b / gcd(a, b);
}
欧拉筛法(含朴素筛法、埃式筛法)
数论之欧拉筛法(含朴素筛选、埃式筛选详细代码)
质数-欧拉筛
模板:
//欧拉筛所需要数组
//flag表示合数数组,true为合数
static boolean[] flag = new boolean[N];
//存储质数
static int[] primes = new int[N];
static int cnt = 0;//欧拉筛
public static void getPrimes(int n) {//遍历所有情况for (int i = 2; i <= n; i++) {if (!flag[i]) primes[cnt++] = i;//枚举所有primes数组中的情况来提前构造合数for (int j = 0; j < cnt && primes[j] * i <= n; j ++) {int pre = primes[j] * i;flag[pre] = true;if (i % primes[j] == 0) break;}}
}//判断是否是质数(由于之前primes数组仅仅开了sqrt(20亿)也就只有50万,所以这里需要进行遍历一遍质数数组来进行判断校验)
public static boolean isPrime(int x) {//若是x在50万范围,直接从flag数组中判断返回即可if (x < N) return !flag[x];//若是>=50万,那么就进行遍历质数数组看是否有能够整除的,如果有那么直接返回for (int i = 0; primes[i] <= x / primes[i]; i++) {if (x % primes[i] == 0) return false;}return true;
}
欧几里得与扩展欧几里得
欧几里得与扩展欧几里得算法(含推导过程及代码)
辗转相除(含辗转相减法)
辗转相除以及辗转相减法
组合数学
容斥定理
容斥定理:能被 a 或 b 整除的数的个数 = 能够被 a 整除的数的个数 + 能够被 b 整除的数的个数 - 既能被 a 又能被 b 整除的数的个数。
题单
leetcode、878. 第 N 个神奇数字(困难)
快速幂
快速幂及矩阵快速幂分析及代码实现
模板:
private static final long MOD = 1000000007;/*** 递归快速幂* @param a 实数a* @param n 阶数n,三种情况,n=0,n=奇数,n=偶数* @return*/
public static long qpow(long a, long n){if (n == 0){return 1;}else if ((n & 1) == 1) { //奇数return qpow(a, n -1) * a % MOD;}else {long temp = qpow(a, n / 2) % MOD;return temp * temp % MOD;}
}/*** 非递归方式*/
public static long qpow2(long a, long n) {long ans = 1;while ( n != 0) {if ((n & 1) == 1) { //若是n为奇数ans *= a % MOD;ans %= MOD;//求模处理}a *= a % MOD; //这个就表示偶数情况a = a % MOD;//求模处理n = n >> 1;}return ans;
}
矩阵
数据结构
哈希表 √
树状数组 √
并查集
线段树 √
#图论 √
树上问题
树的直径
计算机几何
杂项
双指针 √
相关文章:

个人算法题精简导航整理(精炼汇总,含知识点、模板题、题单)
文章目录前言导航注意事项技巧类自定义Pair排序N维数组转一维位运算状态压缩算法基础枚举 √指数型枚举排列型枚举组合型枚举模拟 √日期天数问题:平年闰年情况递归&分治 √贪心 √货仓选址-模板题排序 √归并排序前缀和&差分 √前缀和差分(一维…...

Mac 和 Win,到底用哪个系统学编程?
今天来聊一个老生常谈的问题,学编程时到底选择什么操作系统?Mac、Windows,还是别的什么。。 作为一个每种操作系统都用过很多年的程序员,我会结合我自己的经历来给大家一些参考和建议。 接下来先分别聊聊每种操作系统的优点和不…...
文心一言---中国版的“ChatGPT”狂飙的机会或许要出现了
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三…...
2023最全Python+Selenium环境搭建教程-你绝对想不到有这么简单!
还有视频版本结合项目实战介绍,轻松学习! PythonSelenium自动化测试环境搭建Web自动化测试全套教程_哔哩哔哩_bilibiliPythonSelenium自动化测试环境搭建Web自动化测试全套教程共计180条视频,包括:1、Web自动化测试需求和挑战、2…...

JavaSe第10次笔记
1.Java中,static不能修饰局部变量。 2.构造代码块:可用于成员变量的赋值,但需要注意的是,构造代码块最先执行(比构造方法先)。 3.静态代码块(可用于静态成员变量赋值):写法如下 static { 静态成员操作; } (比构造…...
【C语言笔记】自定义类型全解
【C语言笔记】自定义类型全解一、结构体1、什么是结构体2、结构体的声明与定义2.1、结构体的声明2.2、对结构体成员的访问2.3、对结构体成员的初始化2.4、结构体的不完整声明2.5、结构体嵌套定义3、结构体的自引用3.1、错误的自引用3.2、正确的自引用4、结构体大小的计算4.1、结…...

文心一言硬刚ChatGPT。文心一言能否为百度止颓?中国版ChatGPT“狂飙”的机会在哪儿?
一.文心一言介绍 今天,3月16日消息,百度于北京总部召开新闻发布会,主题围绕新一代大语言模型、生成式AI产品文心一言。百度首席技术官王海峰现在详解了文心一言背后的文心大模型及技术特性。 文心一言是新一代知识增强大语言模型࿰…...
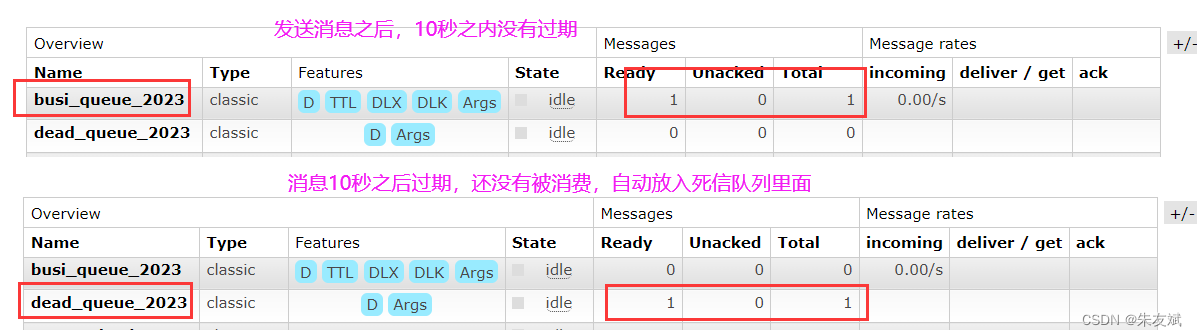
【RabbitMQ笔记10】消息队列RabbitMQ之死信队列的介绍
这篇文章,主要介绍消息队列RabbitMQ之死信队列。 目录 一、RabbitMQ死信队列 1.1、什么是死信队列 1.2、设置过期时间TTL 1.3、配置死信交换机和死信队列(代码配置) (1)设置队列过期时间 (2ÿ…...

Python04 数据序列-字符串
Python04 数据序列-字符串 4.1 字符串概念 字符串是 Python 中最常用的数据类型。我们可以使用引号( ’ 或 " )来创建字符串。 格式: 变量名 数据 / "数据" / """ 数据 """案例: a hello world b &q…...
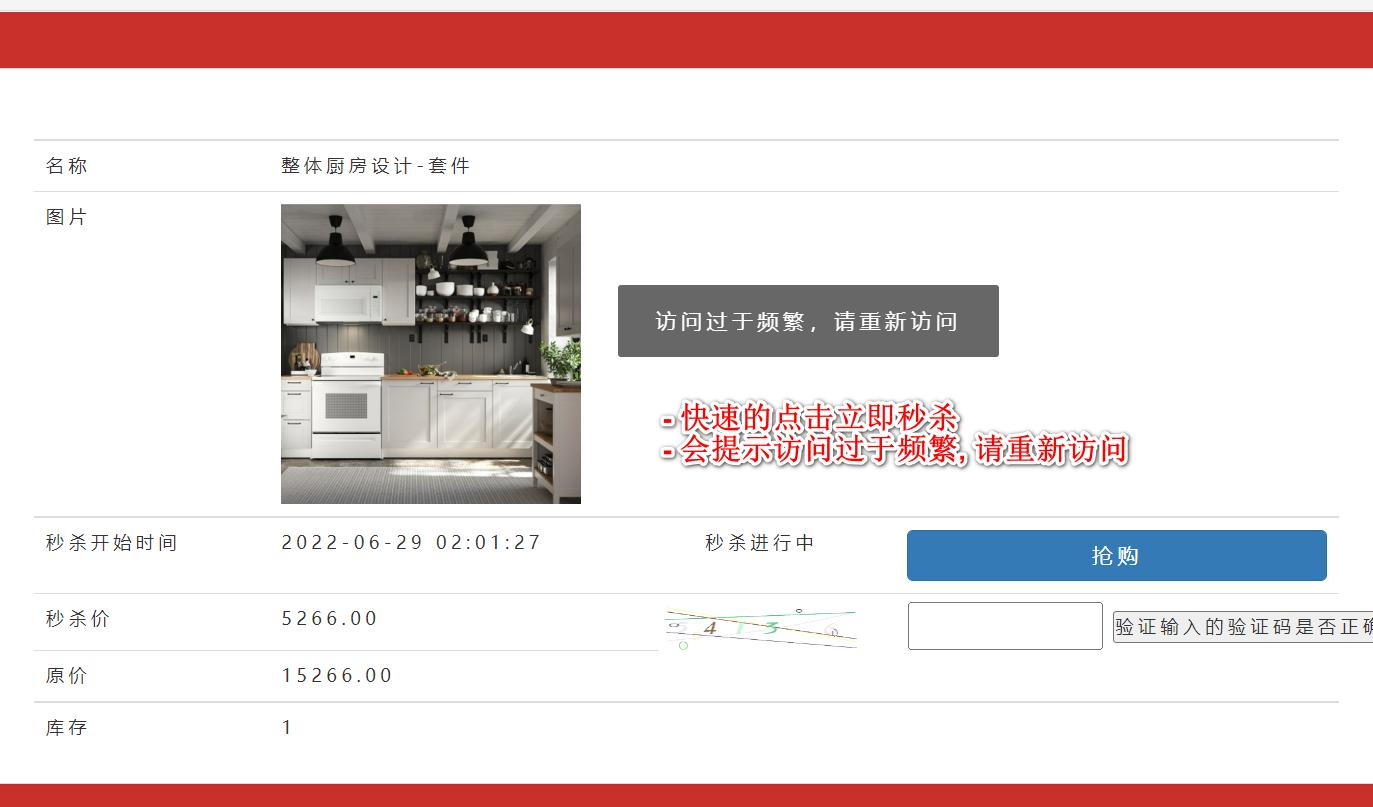
Redis限流接口防刷
Redis限流接口防刷 Redis 除了做缓存,还能干很多很多事情:分布式锁、限流、处理请求接口幂等性。。。太多太多了~ 大家好,我是llp,许久没有写博客了,今天就针对Redis实现接口限流做个记录。废话不多说&am…...
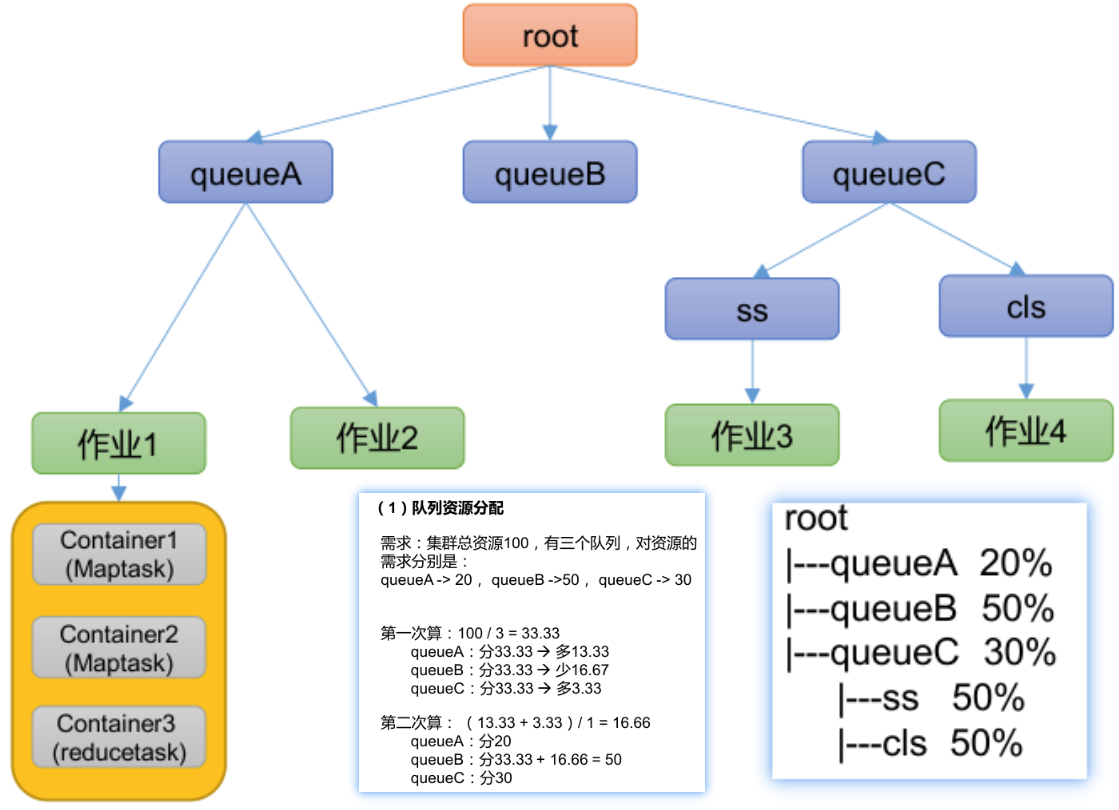
Yarn 资源调度器
Yarn 资源调度器:资源调度平台,负责为运算程序提供服务器运算资源 1 Yarn 基础架构 YARN 主要由 ResourceManager、NodeManager、ApplicationMaster 和 Container 等组件构成。 MR 程序提交到客户端所在的节点。YarnRunner 向 ResourceManager 申请一个…...
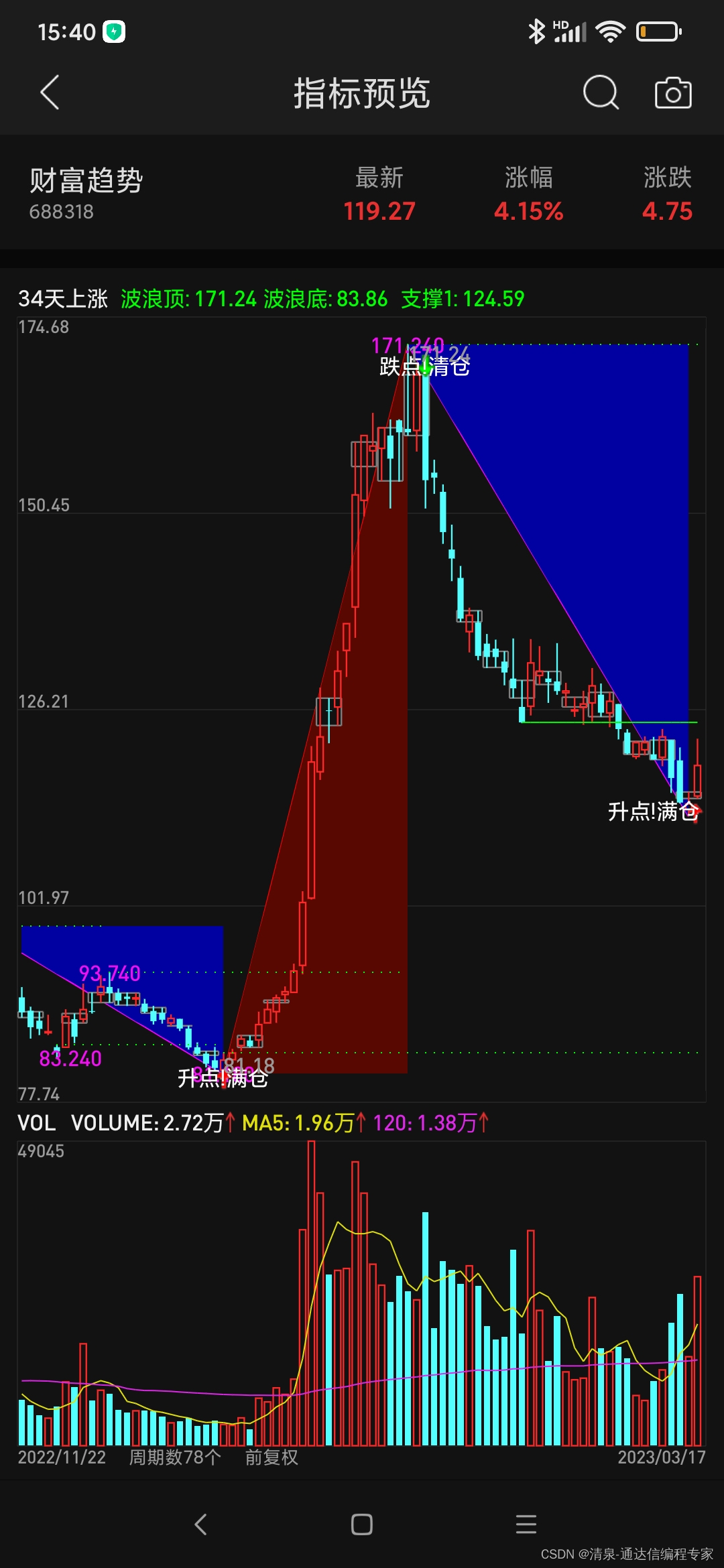
通达信 34日上升三角形主图源码
请先看效果图。 以下是编程源码,可以参考学习一下: N:34;{三角背景} 趋势下:DRAWLINE(HHHV(H,N),H,LLLV(L,N),L,0),LINETHICK2,COLORMAGENTA; SX:REF(趋势下,1)<趋势下; SS:DRAWLINE(SX,趋势下,REF(SX,1),REF(趋势下,1),1); DRAWBAND(SS,RGB(0,0,16…...
)
CSDN周赛第37期题解(Python版)
这期周赛题目和测试集还算完整,没有出现往期的bug。1、题目名称:幼稚班作业幼稚园终于又有新的作业了。 老师安排同学用发给同学的4根木棒拼接成一个三角形。 当然按照正常的逻辑,如果不能拼接成三角形。 必然要折断某个木棍来拼接三角形。 可…...

程序调试方法
调试思路 程序中一定要尽可能的做容错处理,可能会出错的地方,增加打印日志,这样在出问题时候才能最快的定位问题,所以这个属于前置工作,前置做的越多越好,后期调试越省力,程序也更健壮。学会看…...
【Android入门到项目实战--2.3】—— 活动的四种启动模式(standard、singleTop、singleTask、singleInstance)
目录 一、活动的启动模式 1、standard 2、singleTop 3、singleTask 4、singleInstance 本篇文章主要讲解活动的生命周期和活动的启动模式。 一、活动的启动模式 活动的启动模式共有4种,分别是standard、singleTop、singleTask和singleInstance; 可…...
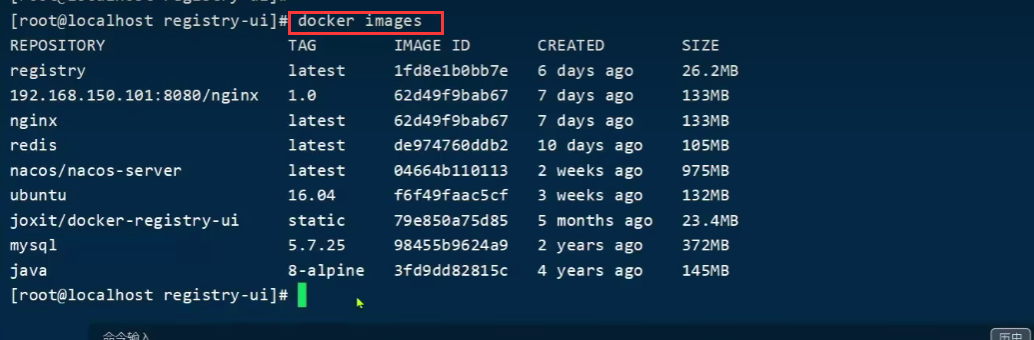
SpringCloud微服务技术栈.黑马跟学(三)
SpringCloud微服务技术栈.黑马跟学 三今日目标1.初识Docker1.1.什么是Docker1.1.1.应用部署的环境问题1.1.2.Docker解决依赖兼容问题1.1.3.Docker解决操作系统环境差异1.1.4.小结1.2.Docker和虚拟机的区别1.3.Docker架构1.3.1.镜像和容器1.3.2.DockerHub1.3.3.Docker架构1.3.4.…...

学习Java——集合类
目录 1.Collection和Collections区别 2.Set和List区别 3.ArrayList和LinkedList和Vector的区别 4.Set如何保证元素不重复 5.Arrays.asList获得的List使用时需要注意什么 1.Collection和Collections区别 Collection 是一个集合接口。 它提供了对集合对象进行基本操作的通用…...
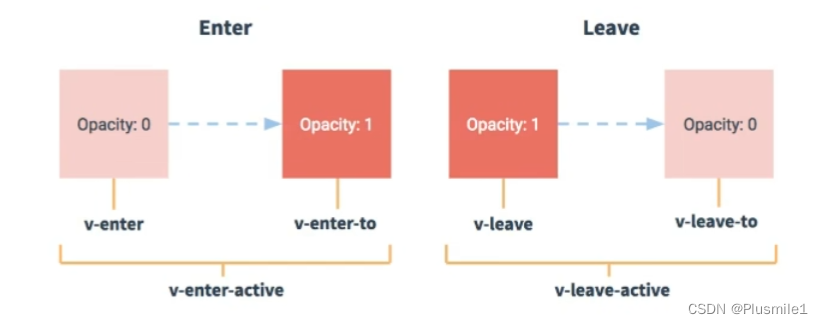
[前端笔记035]vue2之脚手架vue-cli
前言 本笔记参考视频,尚硅谷:BV1Zy4y1K7SH p61 - p95 简介 Vue 脚手架是 Vue 官方提供的标准化开发工具,vue-cli使用步骤 如果下载缓慢请配置 npm 淘宝镜像:npm config set registry http://registry.npm.taobao.org全局安装vue/cli&#…...

《Linux的权限》
本文主要对linux的一些基本权限进行讲解 文章目录前言Linux权限(1)权限的概念(2)linux下用户分类(root,普通)(3)linux的文件属性文件属性的分类文件权限修改文件权限1、chmod2、chown和chgrp3、fiile权限的三个重要的问题第一个问…...

js类型转换
类型转换 1.字符串转换 字符串转换在原来值的基础上加上 "" let num 1 num String(num) // "1"String(false) // "false"2.数字转换 在算数函数和表达式中,会自动进行数字转换。其自动完成的数字转换为隐式转换,也可…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
