【Unity3D】Shader常量、变量、结构体、函数
1 源码路径
Unity Shader 常量、变量、结构体、函数一般可以在 Unity Editor 安装目录下面的【Editor\Data\CGIncludes\UnityShader】目录下查看源码,主要源码文件如下:
- UnityCG.cginc
- UnityShaderUtilities.cginc
- UnityShaderVariables.cginc
2 Shader 常量
#define UNITY_PI 3.14159265359f
#define UNITY_TWO_PI 6.28318530718f
#define UNITY_FOUR_PI 12.56637061436f
#define UNITY_INV_PI 0.31830988618f
#define UNITY_INV_TWO_PI 0.15915494309f
#define UNITY_INV_FOUR_PI 0.07957747155f
#define UNITY_HALF_PI 1.57079632679f
#define UNITY_INV_HALF_PI 0.636619772367f3 Shader 变量
1)时间变量
// Time (t = time since current level load) values from Unity
float4 _Time; // (t/20, t, t*2, t*3)
float4 _SinTime; // sin(t/8), sin(t/4), sin(t/2), sin(t)
float4 _CosTime; // cos(t/8), cos(t/4), cos(t/2), cos(t)
float4 unity_DeltaTime; // dt, 1/dt, smoothdt, 1/smoothdt2)相机和光源的世界坐标
float3 _WorldSpaceCameraPos; // 相机的世界坐标
half4 _WorldSpaceLightPos0; // 光源的世界坐标3)投影参数
// x = 1 or -1 (-1 if projection is flipped)
// y = near plane
// z = far plane
// w = 1/far plane
float4 _ProjectionParams;4)屏幕参数
// x = width
// y = height
// z = 1 + 1.0/width
// w = 1 + 1.0/height
float4 _ScreenParams;5)MVP 矩阵
float4x4 UNITY_MATRIX_M, unity_ObjectToWorld; // [模型空间->世界空间]的变换矩阵M
float4x4 UNITY_MATRIX_V, unity_MatrixV; // [世界空间->观察空间]的变换矩阵V
float4x4 UNITY_MATRIX_P, glstate_matrix_projection; // [观察空间->裁剪空间]的变换矩阵P
float4x4 UNITY_MATRIX_MV, unity_MatrixMV; // [模型空间->观察空间]的变换矩阵MV
float4x4 UNITY_MATRIX_VP, unity_MatrixVP; // [世界空间->裁剪空间]的变换矩阵VP
float4x4 UNITY_MATRIX_MVP, unity_MatrixMVP; // [模型空间->裁剪空间]的变换矩阵MVP
float4x4 UNITY_MATRIX_I_V, unity_MatrixInvV; // V矩阵的逆矩阵
float4x4 UNITY_MATRIX_T_MV, unity_MatrixTMV; // MV矩阵的转置
float4x4 UNITY_MATRIX_IT_MV, unity_MatrixITMV; // MV矩阵的逆转矩阵
float4x4 unity_WorldToObject; // [世界空间->模型空间]的变换矩阵M
说明:unity_ObjectToWorld 与 unity_WorldToObject 互为逆矩阵。
4 Shader 结构体
1)appdata_base
struct appdata_base {float4 vertex : POSITION; // 局部坐标系下顶点坐标float3 normal : NORMAL; // 局部坐标系下法线向量float4 texcoord : TEXCOORD0; // 纹理坐标UNITY_VERTEX_INPUT_INSTANCE_ID
};2)appdata_tan
struct appdata_tan {float4 vertex : POSITION; // 局部坐标系下顶点坐标float4 tangent : TANGENT; // 局部坐标系下切线向量float3 normal : NORMAL; // 局部坐标系下法线向量float4 texcoord : TEXCOORD0; // 纹理坐标UNITY_VERTEX_INPUT_INSTANCE_ID
};3)appdata_full
struct appdata_full {float4 vertex : POSITION; // 局部坐标系下顶点坐标float4 tangent : TANGENT; // 局部坐标系下切线向量float3 normal : NORMAL; // 局部坐标系下法线向量float4 texcoord : TEXCOORD0; // 纹理坐标0float4 texcoord1 : TEXCOORD1; // 纹理坐标1float4 texcoord2 : TEXCOORD2; // 纹理坐标2float4 texcoord3 : TEXCOORD3; // 纹理坐标3fixed4 color : COLOR; // 顶点颜色UNITY_VERTEX_INPUT_INSTANCE_ID
};4)appdata_img
struct appdata_img
{float4 vertex : POSITION; // 局部坐标系下顶点坐标half2 texcoord : TEXCOORD0; // 纹理坐标UNITY_VERTEX_INPUT_INSTANCE_ID
};5)v2f_img
struct v2f_img
{// 作为顶点着色器输出时, pos指裁剪坐标系下的坐标; 作为片元着色器输入时, pos指屏幕坐标系下的坐标float4 pos : SV_POSITION;half2 uv : TEXCOORD0; // 纹理坐标UNITY_VERTEX_INPUT_INSTANCE_IDUNITY_VERTEX_OUTPUT_STEREO
};说明:作为顶点着色器输出时, pos指裁剪坐标系下的坐标; 作为片元着色器输入时, pos指屏幕坐标系下的坐标。
5 Shader 函数
5.1 基础函数
1)数值计算
sign(x)、abs(x) // 符号、绝对值
min(a, b)、max(a, b) // 最值函数
ceil(x)、floor(x)、round(x) // 取整函数
frac(x) // 取小数部分
fmod(x, y) // 取余数
rap(x) // 倒数(1/x)
sqrt(x)、pow(x) // 幂函数
exp(x)、exp2(x) // 指数函数(e^x、2^x)
log(x)、log10(x)、log2(x) // 对数函数
degrees(x)、radians(x) // 角度转换函数
sin(x)、cos(x)、tan(x)、asin(x)、acos(x)、atan(x) // 三角函数
sinh(x)、cosh(x)、tanh(x) // 双曲线函数
saturate(x) // 将x约束在0和1之间, 超过边界就取边界值
clamp(x, min, max) // 将x约束在min和max之间, 超过边界就取边界值
smoothstep (min, max, x) // 平滑比例, 公式: k=saturate((x-min)/(max-min)), y=k*k*(3-2*k)
lerp(a, b, f) // 插值, 公式: y=x+f*(y-x), a、b可以是向量2)向量计算
all(vec) // 如果vec中每个分量都是非零的则返回true, 否则返回false
any(vec) // 如果vec中存在一个分量是非零的则返回true, 否则返回false
distance(pos1, pos2) // 计算pos1与pos2之间的距离
length(vec) // 计算向量的模长
normalize(vec) // 计算向量的单位向量
dot(vec1, vec2) // 向量点乘
cross(vec1, vec2) // 向量叉乘
reflect(i, n) // 根据入射向量和法线向量计算反射向量3)矩阵计算
mul(M, N)、mul(M, v), mul(v, M) // M*N、M*v、M'*v
determinant(M) // 计算矩阵的行列式
transpose(M) // 矩阵转置4)纹理计算
tex2D(sampler2D, uv_Tex) // 查询纹理坐标对应的纹理值
UnpackNormal(color) // 根据法线纹理解析法线向量5.2 坐标和向量变换
1)坐标变换
// 模型空间->观察空间
float3 UnityObjectToViewPos(float3 pos) // mul(UNITY_MATRIX_MV, float4(pos, 1.0)).xyz
float3 UnityObjectToViewPos(float4 pos) // UnityObjectToViewPos(pos.xyz)
// 模型空间->裁剪空间
float4 UnityObjectToClipPos(float3 pos) // mul(UNITY_MATRIX_MVP, float4(pos, 1.0))
float4 UnityObjectToClipPos(float4 pos) // UnityObjectToClipPos(pos.xyz)
// 世界空间->观察空间
float3 UnityWorldToViewPos(float3 pos) // mul(UNITY_MATRIX_V, float4(pos, 1.0)).xyz
// 世界空间->裁剪空间
float4 UnityWorldToClipPos(float3 pos) // mul(UNITY_MATRIX_VP, float4(pos, 1.0))
// 观察空间->裁剪空间
float4 UnityViewToClipPos(float3 pos) // mul(UNITY_MATRIX_P, float4(pos, 1.0))2)向量变换
// 局部空间->世界空间
float3 UnityObjectToWorldDir(float3 dir) // normalize(mul((float3x3)unity_ObjectToWorld, dir))
// 世界空间->局部空间
float3 UnityWorldToObjectDir(float3 dir) // normalize(mul((float3x3)unity_WorldToObject, dir))3)法线变换
// 局部空间->世界空间
float3 UnityObjectToWorldNormal(float3 norm) {
#ifdef UNITY_ASSUME_UNIFORM_SCALING // 统一缩放(x、y、z分量缩放系数一致)return UnityObjectToWorldDir(norm); // normalize(mul((float3x3)unity_ObjectToWorld, norm))
#elsereturn normalize(mul(norm, (float3x3)unity_WorldToObject)); // mul(IT_M, norm) => mul(norm, I_M)
#endif
}法线由切线计算而来,在局部空间中 A 点的切线向量为 v1,法线向量为 n1,经过模型变换(矩阵 M)后,切线向量为 v2,法线向量为 n2,假设法线向量的变换矩阵为 G,因此存在以下关系:

Unity 中线性变换主要有平移、旋转、缩放,由于向量不受平移变换影响,因此,对于法线向量而言,只受旋转和缩放影响。
- 当 M 只包含旋转变换时,M 是正交矩阵,
,因此 G = M;
- 当 M 只包含统一缩放变换时,M = k·E,因此 G = 1/k·E = 1/(k^2)·M,由于法线向量只需要方向,后面会进行归一化,因此可以简写 G = M;
- 当 M 只包含旋转变换和统一缩放变换时,G = 1/(k^2)·M,由于法线向量只需要方向,后面会进行归一化,因此可以简写 G = M;
4)其他变换
// 观察空间->裁剪空间
float2 TransformViewToProjection (float2 v) // mul((float2x2)UNITY_MATRIX_P, v)
float3 TransformViewToProjection (float3 v) // mul((float3x3)UNITY_MATRIX_P, v)5.3 计算指向相机和光源的向量
1)计算顶点指向相机的向量
// _WorldSpaceCameraPos.xyz - worldPos
float3 ObjSpaceViewDir(float4 v) // 输入: 局部坐标, 输出: 局部坐标
float3 WorldSpaceViewDir(float4 localPos) // 输入: 局部坐标, 输出: 世界坐标
float3 UnityWorldSpaceViewDir(float3 worldPos) // 输入: 世界坐标, 输出: 世界坐标2)计算顶点指向光源的向量
// mul(unity_WorldToObject, _WorldSpaceLightPos0).xyz - v.xyz
float3 ObjSpaceLightDir(float4 v) // 输入: 局部坐标, 输出: 局部坐标
float3 WorldSpaceLightDir(float4 localPos) // 输入: 局部坐标, 输出: 世界坐标
float3 UnityWorldSpaceLightDir(float3 worldPos) // 输入: 世界坐标, 输出: 世界坐标相关文章:
【Unity3D】Shader常量、变量、结构体、函数
1 源码路径 Unity Shader 常量、变量、结构体、函数一般可以在 Unity Editor 安装目录下面的【Editor\Data\CGIncludes\UnityShader】目录下查看源码,主要源码文件如下: UnityCG.cgincUnityShaderUtilities.cgincUnityShaderVariables.cginc 2 Shader 常…...

LeetCode 刷题系列 -- 496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。对于每个 0 < i < nums1.length ,找出满…...
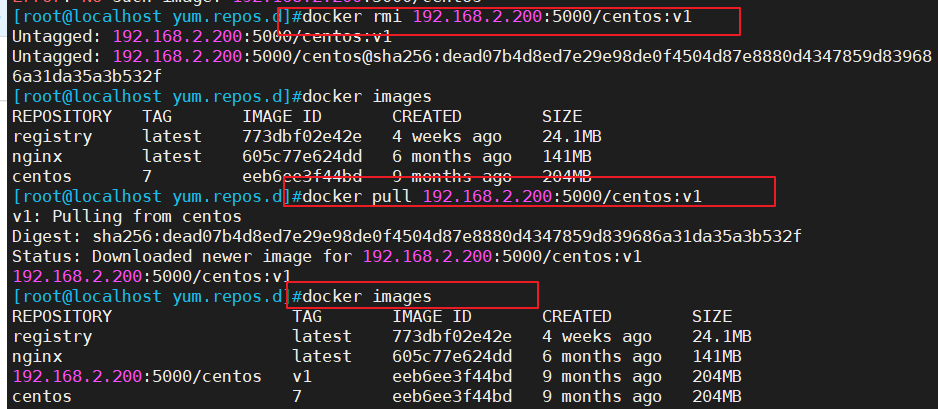
Docker 搭建本地私有仓库
一、搭建本地私有仓库有时候使用Docker Hub这样的公共仓库可能不方便,这种情况下用户可以使用registry创建一个本地仓库供私人使用,这点跟Maven的管理类似。使用私有仓库有许多优点:1)节省网络带宽,针对于每个镜像不用…...

XML中的CDATA且mybatis中特殊字符转义
如果想看如果CDATA在mybatis的xml文件中使用的可以直接跳转。 CDATA1 XML中的CDATA1.1 为什么叫CDATA1.2 CDATA在XML中的语法1.3 CDATA在XML中的例子1.4 CDATA规则2 Mybatis中的CDATA2.1 Mybatis中使用XML转义序列转义2.2 Mybatis中使用CDATA转义2.3 mybatis中使用CDATA需注意的…...

位运算 | 1356. 根据数字二进制下 1 的数目排序
LeetCode 1356. 根据数字二进制下 1 的数目排序 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小升序排列。 文章讲解https://www.programmercarl.com/1356.%…...

React Hooks之useState详解
1. 什么是Hooks? React官方简介:Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性。 本文中讲解的useState就是React中的其中一个Hook。 2. useState useState 通过在函数组件里调用它来满足给组件添…...

选购交换机的参数依据和主要的参数指标详解
如何选购交换机?用什么交换机?在选购交换机时交换机的优劣无疑十分的重要,而交换机的优劣要从总体构架、性能和功能三方面入手。交换机选购时。性能方面除了要满足RFC2544建议的基本标准,即吞吐量、时延、丢包率外,随着…...
)
Connext DDS属性配置参考大全(1)
介绍属性QoS策略存储名称/值(字符串)对,可用于配置Connext DDS的某些参数,这些参数未通过正式的QoS策略公开。 属性QoS策略存储实体的名称/值对。名称和值都是字符串。在核心库用户手册的“Property QosPolicy(DDS Extension)”部分中找到有关RTI Connext DDS属性QoS的更…...
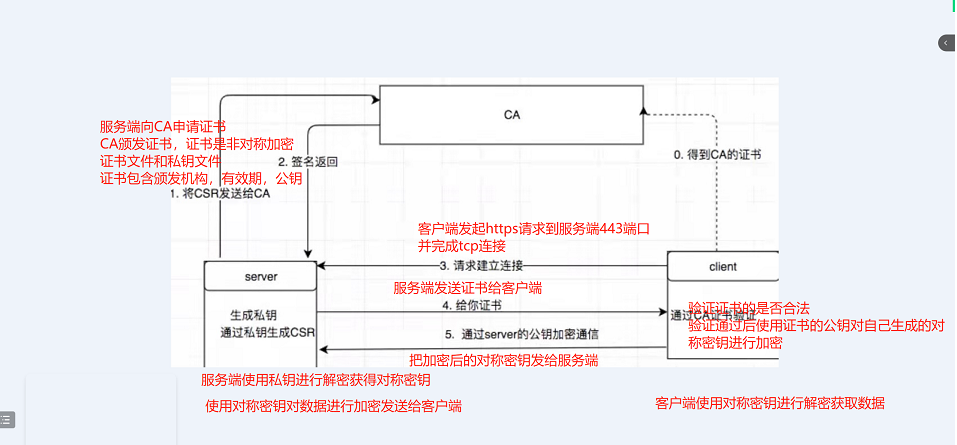
Docker安全
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。 与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃 一、Docker 容器与虚拟机的区别 1、隔…...

刷题记录:牛客NC20279[SCOI2010]序列操作
传送门:牛客 题目描述: lxhgww最近收到了一个01序列,序列里面包含了n个数,这些数要么是0,要么是1,现在对于这个序列有五种变换操作和询问操作: 0 a b 把[a, b]区间内的所有数全变成0 1 a b 把[a, b]区间内的所有数全…...

Fluent Python 笔记 第 6 章 使用一等函数实现设计模式
虽然设计模式与语言无关,但这并不意味着每一个模式都能在每一门语言中使用。1996 年,Peter Norvig 在题为“Design Patterns in Dynamic Languages”(http://norvig.com/design- patterns/)的演讲中指出,Gamma 等人合著的《设计模式:可复用面…...

windbg-应用层实时调试
调试符号windbg使用一个或多个目录来存放符号条件,并使用环境变量_NT_SYMBOL_PATH来指向这些环境变量的位置,对操作系统内部模块的符号文件,一般用http://msdl.microsoft.com/download/symbols配置如下:SRV*C:\Symbols*http://msd…...

【Python语言基础】——Python NumPy 数组索引
Python语言基础——Python NumPy 数组索引 文章目录 Python语言基础——Python NumPy 数组索引一、Python NumPy 数组索引一、Python NumPy 数组索引 访问数组元素 数组索引等同于访问数组元素。 您可以通过引用其索引号来访问数组元素。 NumPy 数组中的索引以 0 开头,这意味…...
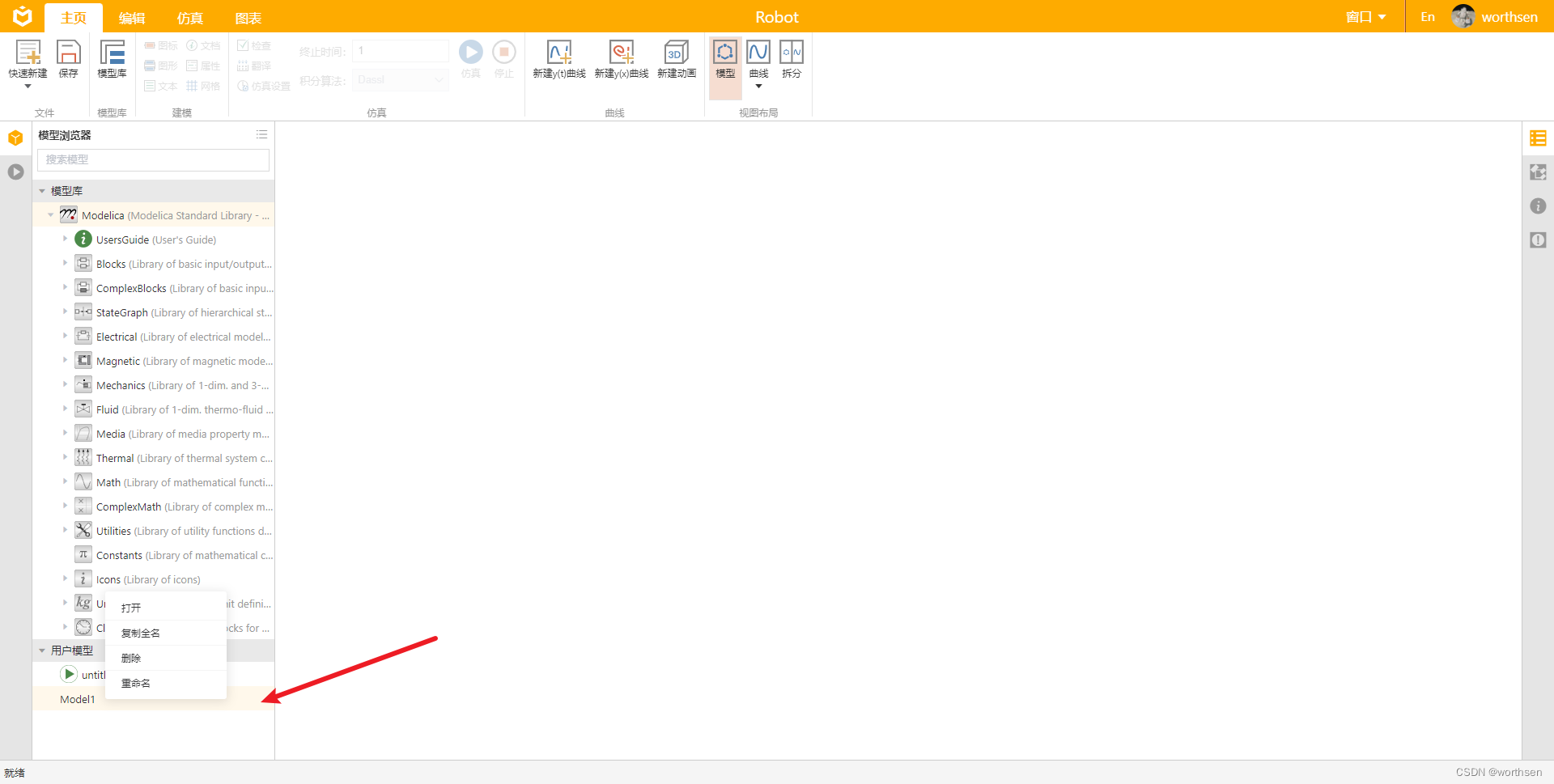
MWORKS--MoHub介绍
MWORKS--MoHub介绍1 介绍1.1 简介1.2 功能特征2 快速上手2.1 进入工作台2.2 新建仓库并进入建模空间2.3 建模进入建模工作空间加载模型库新建模型2.4 仿真2.5 后处理曲线、动画2.6 查看模型信息3 使用手册参考1 介绍 1.1 简介 MWORKS.MoHub 支持工业知识、经验、数据的模型化…...
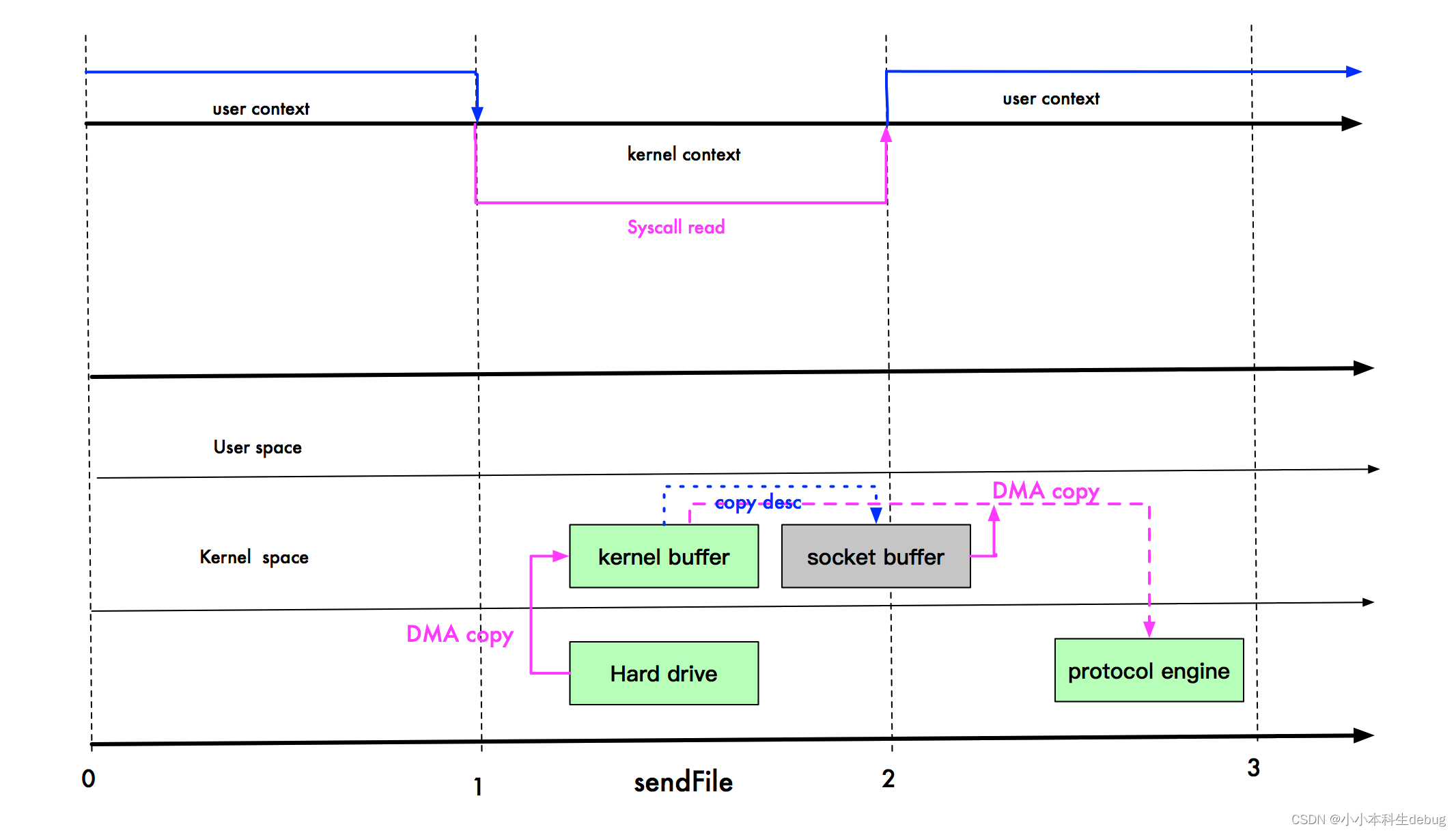
Netty零拷贝机制
Netty零拷贝机制一:用户空间与内核空间二:传统IO流程三:零拷贝常见的实现方式1. mmap write2. sendfile四:Java中零拷贝五:Netty 中如何实现零拷贝1. CompositeByteBuf 实现零拷贝2. wrap 实现零拷贝3. slice 实现零拷…...
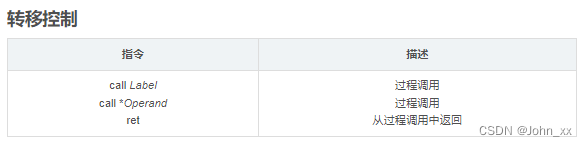
C++:提高篇: 栈-寄存器和函数状态:windows X86-64寄存器介绍
寄存器1、什么是寄存器2、寄存器分类3、windows X86寄存器命名规则4、寄存器相关术语5、寄存器分类5.1、RAX(accumulator register)5.2、RBX(Base register)5.3、RDX(Data register)5.4、RCX(counter register)5.5、RSI(Source index)5.6、RDI(Destination index)5.7、RSP(stac…...
MyBatis-Plus入门案例
MyBatis-Plus入门案例一、MyBatis-Plus简介1、简介2、特性3、支持数据库4、框架结构5、代码及文档地址二、入门案例1、开发环境2、建库建表3、创建Spring Boot工程a>初始化工程b>引入依赖4、编写代码a>配置application.yml 或者 application.propertiesb>添加实体c…...
适用于 Windows 11/10/8/7 的 10 大数据恢复软件分享
适用于 Windows 11/10/8/7 的 最佳数据恢复软件综述。选择首选的专业数据/文件恢复软件,轻松恢复丢失的数据或删除的照片、视频等文件、SSD、外接硬盘、USB、SD卡等存储设备中的文件等。流行的sh流行的数据恢复软件也包括在内。 10 大数据恢复软件分享 为了帮助您恢…...

在线支付系列【23】支付宝支付接入指南
有道无术,术尚可求,有术无道,止于术。 文章目录前言接入指南1. 创建应用2. 绑定应用3. 配置密钥4. 上线应用5. 开通产品沙箱环境开发前准备(沙箱环境)1. 获取参数、秘钥、证书2. 下载支付宝客户端3. 案例演示前言 在之…...
linux系统常用命令
目录 一、系统介绍 二、Linux常用命令 1、Linux命令格式 2、文件目录操作命令:ls 3、文件目录操作命令:cd 4、文件目录操作命令:cat 5、文件目录操作命令:more 6、文件目录操作命令:tail 7、创建文件命令&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
