基于鲸鱼算法的极限学习机(ELM)分类算法-附代码
基于鲸鱼算法的极限学习机(ELM)分类算法
文章目录
- 基于鲸鱼算法的极限学习机(ELM)分类算法
- 1.极限学习机原理概述
- 2.ELM学习算法
- 3.分类问题
- 4.基于鲸鱼算法优化的ELM
- 5.测试结果
- 6.参考文献
- 7.Matlab代码
摘要:本文利用鲸鱼算法对极限学习机进行优化,并用于分类问题
1.极限学习机原理概述
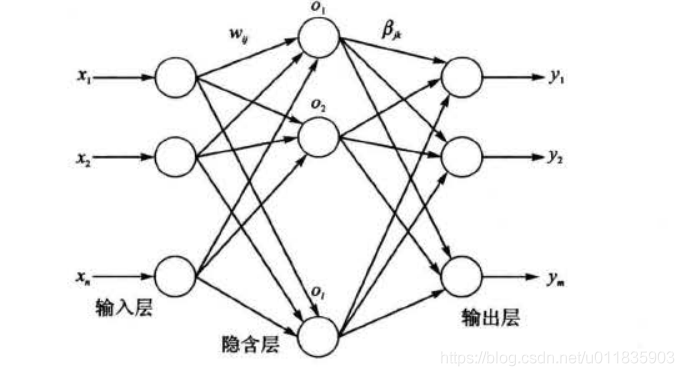
典型的单隐含层前馈神经网络结构如图1 所示,由输入层、隐含层和输出层组成,输 入层与隐含层、隐含层与输出层神经元间全连接。其中,输入层有 n 个神经元,对应 n 个输入变量, 隐含层有 l个神经元;输出层有 m 个神经元 ,对应 m 个输出变量 。 为不失一般性,设输 入层与隐含层间的连接权值 w 为:
w=[w11w12...w1,nw21w22...w2n...wl1wl2...wln](1)w =\left[\begin{matrix}w_{11}&w_{12}&...&w_{1,n}\\ w_{21}&w_{22}&...&w_{2n}\\ ...\\ w_{l1}&w_{l2}&...&w_{ln} \end{matrix}\right]\tag{1} w=w11w21...wl1w12w22wl2.........w1,nw2nwln(1)
其中,wnw_nwn表示输入层第iii个神经元与隐含层第jjj个神经元间的连接权值。
设隐含层与输出层间的连接权值 , 为β\betaβ:
β=[β11β12...β1mβ21β22...β2m...βl1βl2...βlm](2)\beta =\left[\begin{matrix} \beta_{11}&\beta_{12}&...&\beta_{1m}\\ \beta_{21}&\beta_{22}&...&\beta_{2m}\\ ...\\ \beta_{l1}&\beta_{l2}&...&\beta_{lm} \end{matrix}\right] \tag{2} β=β11β21...βl1β12β22βl2.........β1mβ2mβlm(2)
其中,自βjk\beta_{jk}βjk表示隐含层第 j 个神经元与输出层第 k个神经元间的连接权值。
设隐含层神经元的阈值值 b 为:
b=[b1b2...bl](3)b =\left[\begin{matrix}b_1\\ b_2\\ ...\\ b_l \end{matrix}\right]\tag{3} b=b1b2...bl(3)
设具有 Q 个样本的训练集输入矩阵 X 和输出矩阵 Y 分别为
X=[x11x12...x1Qx21x22...x2Q...xn1xn2...xnQ](4)X =\left[\begin{matrix}x_{11}&x_{12}&...&x_{1Q}\\ x_{21}&x_{22}&...&x_{2Q}\\ ...\\ x_{n1}&x_{n2}&...&x_{nQ} \end{matrix}\right]\tag{4} X=x11x21...xn1x12x22xn2.........x1Qx2QxnQ(4)
KaTeX parse error: Undefined control sequence: \matrix at position 11: Y =\left[\̲m̲a̲t̲r̲i̲x̲{y_{11},y_{12},…
设隐含层神经元的激活函数为 g(x),则由图1 可得, 网络的输出 T 为:
T=[t1,..,tQ]m∗Q,tj=[t1j,...,tmj]T=[∑i=1tβi1g(wixj+bi)∑i=1tβi2g(wixj+bi)...∑i=1tβimg(wixj+bi)]m∗1,(j=1,2,...,Q)(6)T = [t_1,..,t_Q]_{m*Q},t_j = [t_{1j},...,t_{mj}]^T =\left[\begin{matrix}\sum_{i=1}^t\beta_{i1}g(w_ix_j + b_i)\\ \sum_{i=1}^t\beta_{i2}g(w_ix_j + b_i)\\ ...\\ \sum_{i=1}^t\beta_{im}g(w_ix_j + b_i) \end{matrix}\right]_{m*1},(j=1,2,...,Q)\tag{6} T=[t1,..,tQ]m∗Q,tj=[t1j,...,tmj]T=∑i=1tβi1g(wixj+bi)∑i=1tβi2g(wixj+bi)...∑i=1tβimg(wixj+bi)m∗1,(j=1,2,...,Q)(6)
式(6)可表示为:
Hβ=T’(7)H\beta = T’ \tag{7} Hβ=T’(7)
其中, T’为矩阵 T 的转置; H 称为神经网络的隐含层输出矩阵 , 具体形式如下 :
H(w1,...,wi,b1,...,bl,x1,...,xQ)=[g(w1∗x1+b1)g(w2∗x1+b2)...g(wl∗x1+bl)g(w1∗x2+b1)g(w2∗x2+b2)...g(wl∗x2+bl)...g(w1∗xQ+b1)g(w2∗xQ+b2)...g(wl∗xQ+bl)]Q∗lH(w_1,...,w_i,b_1,...,b_l,x_1,...,x_Q) =\left[\begin{matrix} g(w_1*x_1 + b_1)&g(w_2*x_1 + b_2)&...&g(w_l*x_1 + b_l)\\ g(w_1*x_2 + b_1)&g(w_2*x_2 + b_2)&...&g(w_l*x_2 + b_l)\\ ...\\ g(w_1*x_Q + b_1)&g(w_2*x_Q + b_2)&...&g(w_l*x_Q + b_l) \end{matrix}\right]_{Q*l} H(w1,...,wi,b1,...,bl,x1,...,xQ)=g(w1∗x1+b1)g(w1∗x2+b1)...g(w1∗xQ+b1)g(w2∗x1+b2)g(w2∗x2+b2)g(w2∗xQ+b2).........g(wl∗x1+bl)g(wl∗x2+bl)g(wl∗xQ+bl)Q∗l
2.ELM学习算法
由前文分析可知,ELM在训练之前可以随机产生 w 和 b , 只需确定隐含层神经元个数及隐含层和神经元的激活函数(无限可微) , 即可计算出β\betaβ 。具体地, ELM 的学习算法主要有以下几个步骤:
(1)确定隐含层神经元个数,随机设定输入层与隐含层间的连接权值 w 和隐含层神经元的偏置 b ;
(2) 选择一个无限可微的函数作为隐含层神经元的激活函数,进而计算隐含层输出矩 阵 H ;
(3)计算输出层权值:β=H+T′\beta = H^+T'β=H+T′
值得一提的是,相关研究结果表明,在 ELM 中不仅许多非线性激活函数都可以使用(如 S 型函数、正弦函数和复合函数等),还可以使用不可微函数,甚至可以使用不连续的函数作为激 活函数。
3.分类问题
本文对乳腺肿瘤数据进行分类。采用随机法产生训练集和测试集,其中训练集包含 500 个样本,测试集包含 69 个样本 。
4.基于鲸鱼算法优化的ELM
鲸鱼算法的具体原理参考博客:https://blog.csdn.net/u011835903/article/details/107559167
由前文可知,ELM的初始权值和阈值都是随机产生。每次产生的初始权值和阈值具有满目性。本文利用鲸鱼算法对初始权值和阈值进行优化。适应度函数设计为训练集的错误率与测试集的错误率的和,以期望使训练得到的网络在测试集和训练集上均有较好的结果:
fitness=argmin(TrainErrorRate+TestErrorRate)。fitness = argmin(TrainErrorRate + TestErrorRate)。 fitness=argmin(TrainErrorRate+TestErrorRate)。
5.测试结果
鲸鱼算法相关参数如下:
%训练数据相关尺寸
R = size(Pn_train,1);
S = size(Tn_train,1);
N = 20;%隐含层个数
%% 定义鲸鱼优化参数
pop=20; %种群数量
Max_iteration=50; % 设定最大迭代次数
dim = N*R + N*S;%维度,即权值与阈值的个数
lb = [-1.*ones(1,N*R),zeros(1,N*S)];%下边界
ub = [ones(1,N*R),ones(1,N*S)];%上边界
将经过鲸鱼优化后的SSA-ELM与基础ELM进行对比。
预测结果如下图
鲸鱼收敛曲线如下:
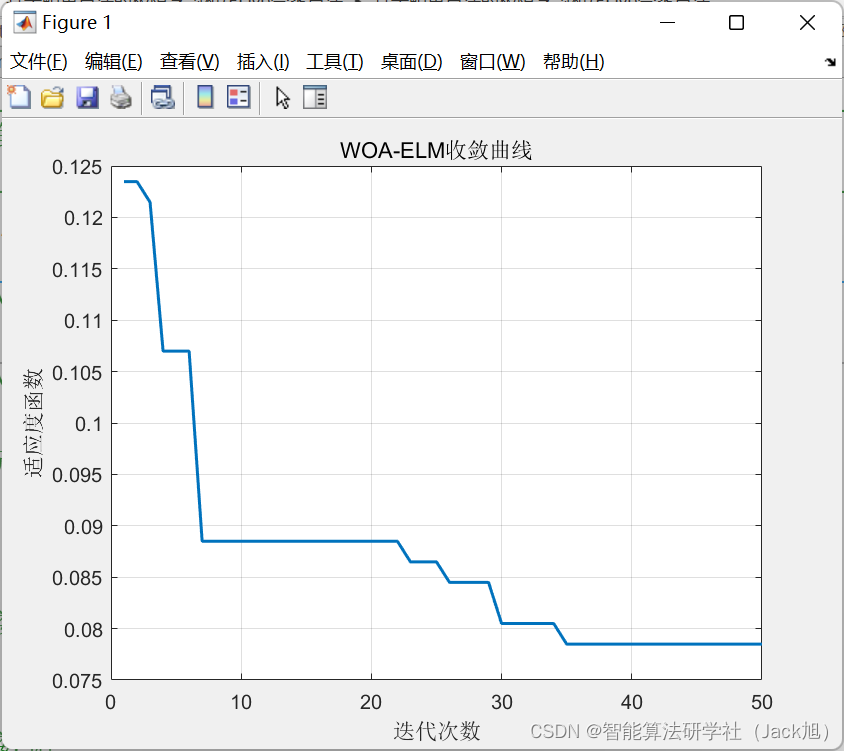
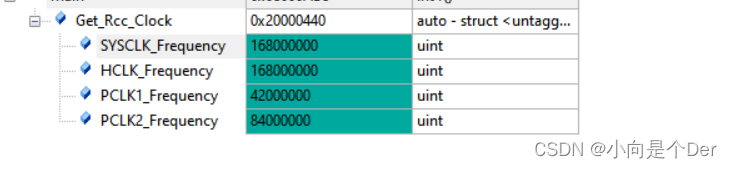
数据结果如下:
鲸鱼优化ELM结果展示:----------------
训练集正确率Accuracy = 93.6%(468/500)
测试集正确率Accuracy = 98.5507%(68/69)
病例总数:569 良性:357 恶性:212
训练集病例总数:500 良性:313 恶性:187
测试集病例总数:69 良性:44 恶性:25
良性乳腺肿瘤确诊:44 误诊:0 确诊率p1=100%
恶性乳腺肿瘤确诊:24 误诊:1 确诊率p2=96%
传统ELM结果展示:----------------
训练集正确率Accuracy = 90.2%(451/500)
测试集正确率Accuracy = 94.2029%(65/69)
病例总数:569 良性:357 恶性:212
训练集病例总数:500 良性:313 恶性:187
测试集病例总数:69 良性:44 恶性:25
良性乳腺肿瘤确诊:43 误诊:1 确诊率p1=97.7273%
恶性乳腺肿瘤确诊:22 误诊:3 确诊率p2=88%
从上述数据可以看出,鲸鱼-ELM训练得到的网络,无论是在测试集和训练集上的正确率均高于基础ELM训练得到的网络。鲸鱼-ELM具有较好的性能。
6.参考文献
书籍《MATLAB神经网络43个案例分析》
7.Matlab代码
相关文章:

基于鲸鱼算法的极限学习机(ELM)分类算法-附代码
基于鲸鱼算法的极限学习机(ELM)分类算法 文章目录基于鲸鱼算法的极限学习机(ELM)分类算法1.极限学习机原理概述2.ELM学习算法3.分类问题4.基于鲸鱼算法优化的ELM5.测试结果6.参考文献7.Matlab代码摘要:本文利用鲸鱼算法对极限学习机进行优化,并用于分类问…...

一文彻底读懂webpack常用配置
开发环境 const webpack require("webpack"); const path require(path) module.exports {// entry: {// a: ./src/0706/a.js,// c: ./src/0706/c.js,// },entry: "./src/0707/reactDemo.js",output: {filename: [name]_dist.js,path: path.resolve(__…...

大环境不好,找工作太难?三面阿里,幸好做足了准备,已拿offer
三面大概九十分钟,问的东西很全面,需要做充足准备,就是除了概念以外问的有点懵逼了(呜呜呜)。回来之后把这些题目做了一个分类并整理出答案(强迫症的我狂补知识)分为软件测试基础、Python自动化…...
)
C++ 手撸简易服务器(完善版本)
本文没有带反射部分内容,可以看我之前发的 Server.h #pragma once#include <string> #include <iostream> #include <thread> #include <unordered_map> using namespace std; #ifndef _SERVER_ #define _SERVER_#include <winsock.h&…...

【Python入门第三十四天】Python丨文件处理
文件处理是任何 Web 应用程序的重要组成部分。 Python 有几个用于创建、读取、更新和删除文件的函数。 文件处理 在 Python 中使用文件的关键函数是 open() 函数。 open() 函数有两个参数:文件名和模式。 对于刚学Python的小伙伴,我给大家准备了2023…...
【Linux】写一个基础的bash
头文件#include<stdio.h> #include<stdlib.h> #include<unistd.h> #include<sys/wait.h> #include<sys/stat.h> #include<string.h> #include<pwd.h> #include<dirent.h>分割输入的命令串字符串或参数内容为空则退出strtok( ,…...
图解如何一步步连接远程服务器——基于VScode
基于VScode连接远程服务器 安装Remote-SSH等插件 想要在vscode上连接远程服务器需要下载Remote-SSH系列插件: 直接在插件中搜索remote,即可找到,选择图片中的3个插件,点击install安装。 配置Remote-SSH 在这个步骤有多种操作…...

element - - - - - 你不知道的loading使用方式
求人不如求己 你不知道的loading使用方式1. 指令方式使用1.1 默认loading1.2 自定义loading1.3 整页加载2. 服务方式使用2.1 this.$loading的使用2.2 Loading.service的使用关于页面交互,最害怕的就是接口等待时间太长,用户体验不好。 而如何提高用户体…...

C++程序调用IsBadReadPtr或IsBadWritePtr引发内存访问违例问题的排查
目录 1、问题描述 2、VS中看不到有效的信息,尝试使用Windbg去分析 3、使用Windbg分析 4、最后...

IntelliJIDEA 常用快捷键
IntelliJIDEA 常用快捷键 Alt Enter 导入包,自动修正,自动创建变量名。 Ctrl Alt O 优化导入的类和包 Ctrl / 单行注释 (//) Ctrl Shift / 多行注释 (/* … */) 方法或类说明注释(文档注释) 在一个方法或类的开头…...

Python自动化抖音自动刷视频
环境准备 Python3.5以上Appium Server服务器Android SDK,需要用到adb服务需要依赖Appium-Python-Client组件库真机或者模拟器,推荐模拟器(真机一般安卓8版本以上了,appium对安卓8以上版本元素获取的兼容性不太好)JDK8环境 实现 确保adb服务…...

使用vite创建vue3工程
定义 什么是vite?-----新一代前端构建工具 优势 开发环境中,无需打包操作,可快速的冷启动---最牛的地方轻量快速的热重载(HMR)---一修改代码就局部刷新,webpack也具备,但vite更快真正的按需编…...
嵌入式学习笔记——STM32的时钟树
时钟树前言时钟树时钟分类时钟树框图LSI与LSEHSI、HSE与PLL系统时钟的产生举例AHB、APBx的时钟配置时钟树相关寄存器介绍1.时钟控制寄存器(RCC_CR)2.RCC PLL 配置寄存器 (RCC_PLLCFGR)3.RCC 时钟配置寄存器 (RCC_CFGR)4.RCC 时钟中断寄存器 (RCC_CIR)修改…...
-NumPy矩阵与通用函数)
Python学习(2)-NumPy矩阵与通用函数
文章首发于:My Blog 欢迎大佬们前来逛逛 1. NumPy矩阵 1.1 mat函数 matasmatrix asmatrix(data, dtypeNone):data:表示输入的数组或者字符串,使用‘,’分割列,使用‘;’分割行 创建两个普通的矩阵&…...

剑指 Offer II 035. 最小时间差
题目链接 剑指 Offer II 035. 最小时间差 mid 题目描述 给定一个 24小时制(小时:分钟 "HH:MM")的时间列表,找出列表中任意两个时间的最小时间差并以分钟数表示。 示例 1: 输入:timePoints [“23:59”,“0…...

Spark SQL函数定义【博学谷学习记录】
1 如何使用窗口函数窗口函数格式:分析函数 over(partition by xxx order by xxx [asc|desc] [rows between xxx and xxx])学习的相关分析函数有那些? 第一类: row_number() rank() dense_rank() ntile()第二类: 和聚合函数组合使用 sum() avg() max() min() count()第三类: la…...
模拟实现STL容器之vector
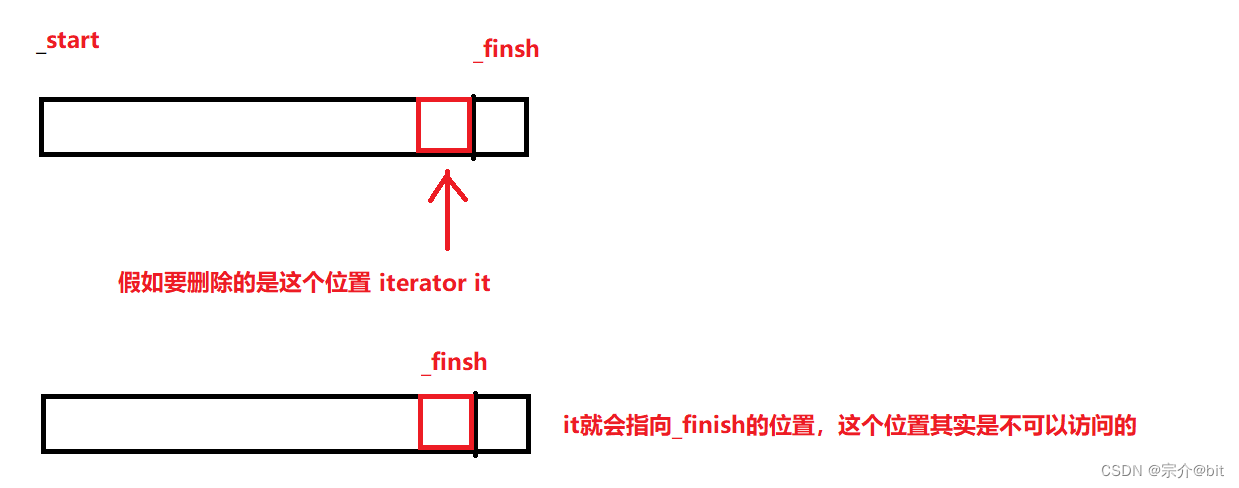
文章目录前言1.大体思路2.具体代码实现1.类模板的创建2.构造函数1.无参构造2.拷贝构造 迭代器构造和给定n个val值构造以及析构函数3.空间扩容1.reserve2.resize4.操作符重载1.[ ]重载2.赋值运算符重载5.数据增加和删除1.尾插2.任意位置插入3.任意位置删除4.尾删6.一些其他接口3…...

ChatGPT-4.0 : 未来已来,你来不来
文章目录前言ChatGPT 3.5 介绍ChatGPT 4.0 介绍ChatGPT -4出逃计划!我们应如何看待ChatGPT前言 好久没有更新过技术文章了,这个周末听说了一个非常火的技术ChatGPT 4.0,于是在闲暇之余我也进行了测试,今天这篇文章就给大家介绍一…...
)
Java反射(详细学习笔记)
Java反射 1. Java反射机制概述 Reflection(反射)是java被视为java动态语言的关键,反射机制允许程序在执行期间借助于Reflection API获取任何类的内部信息,并能直接操作任意对象的内部属性及方法。 Class c Class.forName(&quo…...
学习 Python 之 Pygame 开发魂斗罗(十二)
学习 Python 之 Pygame 开发魂斗罗(十二)继续编写魂斗罗1. 修改玩家扣减生命值2. 解决玩家下蹲子弹不会击中玩家而是直接让玩家死亡的问题3. 完善地图4. 增加产生敌人函数,解决一直产生敌人的问题5. 给玩家类增加计算玩家中心的方法继续编写魂…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
