动态规划之路径问题
动态规划算法介绍
基本原理和解题步骤
针对于动态规划的题型,一般会借助一个 dp 表,然后确定这个表中应该填入什么内容,最终直接返回表中的某一个位置的元素。
细分可以分为以下几个步骤:
-
创建 dp 表以及确定 dp 表中所要填写位置的含义:这一步关乎到最终推导出的状态转移方程,一般是根据题意或者根据以往做题的经验得出的。一般要么是以某一个位置结尾进行分析,要么是以某一个位置为开头进行分析。
-
确定状态转移方程:是指针对 dp 表中的某一个单独分析,这个位置应该填入什么值。在进行这一步时,可以假设确定该位置元素时所需要的所有其他位置的值都已经确定了。
-
初始化:有些题目,在创建完 dp 表之后,如果直接用状态转移方程填表,会导致越界的情况,所以要在某些会越界的位置单独进行初始化。
-
确定填写 dp 表时的填写顺序:dp 表并不一定是从前往后填写的,因为有可能推导出的状态转移方程中,某一个位置中元素的值是跟该位置之后的位置有关的,所以填表顺序也应该结合题意和状态转移方程决定。
-
确定返回值:根据题目要求找出应该返回 dp 表中的哪一个值。
例题
力扣 91. 解码方法
创建 dp 表以及确定 dp 表中所要填写位置的含义:
这道题中,根据解题经验,需要以某一个位置为结尾进行分析,即 dp[i] 表示在字符串 s 中,从开头到 i 位置这段子字符串中一共有多少种解码方法。
确定状态转移方程:
这道题的状态转移方程并不是一成不变的,需要分情况进行讨论。

所以,状态转移方程可以表示为 dp[i] = dp[i - 1] + dp[i - 2],也就是上述两种情况的和。
初始化:
由于推导出的状态转移方程中,dp[i] 的计算需要用到前两个位置的值,所以在开始填表之前,为了防止越界,需要先初始化确定 dp[0] 和 dp[1]。
dp[0]:第一个元素只能单独解码,解码成功为 1,解码失败为 0。
dp[1]:第二个元素可以单独解码,也可以和第一个元素一起解码,单独解码成功为 1,失败为0;单独解码不成功但是和前一个元素一起解码成功为 1,失败为0;单独解码成功,和前一个元素一起解码也成功为 2。
确定填表顺序:
由状态转移方程可以看出应该是从前向后填表。
确定返回值:
该题目需要返回以最后一个位置为结尾的字符串所有可能的解码总数,所以应该返回 dp[n - 1]。
代码:
class Solution
{
public:int numDecodings(string s) {// 创建 dp 表int n = s.size();vector<int> dp(n);// 初始化if (s[0] == '0') return 0;dp[0] = 1;if (n == 1) return dp[0];if (s[1] != '0') dp[1] += 1;int t = (s[0] - '0') * 10 + (s[1] - '0');if (t >= 10 && t <= 26) dp[1] += 1;// 填表for (int i = 2; i < n; i++) {if (s[i] != '0') dp[i] += dp[i - 1];t = (s[i - 1] - '0') * 10 + (s[i] - '0');if (t >= 10 && t <= 26) dp[i] += dp[i - 2];}return dp[n - 1];}
};但是,上面的初始化其实看起来有一些繁琐,可以通过增加虚拟节点的方式让代码变得更简洁。
说白了,就是在状态转移方程会越界的地方增加虚拟节点,并确保这个节点中的值不影响真正节点中填入的正确数据。
在这道题中,可以在 dp 的最前面增加一个位置,并初始化为 1,然后就只需要对字符串 s 的第一个字符进行判断,从第二个字符开始就可以使用状态转移方程了。
但是,注意,增加了一个虚拟节点之后,使用状态转移方程时要注意字符的下标是否和 dp 表的下标对应。
更改后的代码:
class Solution
{
public:int numDecodings(string s) {// 创建 dp 表int n = s.size();vector<int> dp(n + 1);// 初始化dp[0] = 1;dp[1] = s[1 - 1] != '0';// 填表for (int i = 2; i <= n; i++) {if (s[i - 1] != '0') dp[i] += dp[i - 1];int tmp = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];}return dp[n];}
};动态规划中的路径问题
力扣 62. 不同路径
力扣 62. 不同路径
这道题中的路径可以模拟为一个 m 行 n 列的二维数组。
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
其次,由于要记录路径中的每一个位置,所以这道题的 dp 表应该是一个m 行 n 列的二维数组。
每一个位置的含义,也就是 dp[i][j] 指的是,从(0, 0)到 (i,j)位置一共有多少种路径。
确定状态转移方程:
题目指出,每一次移动只能向下或者向右移动,所以到达(i,j)位置之前的一个位置一定是(i - 1,j)或者(i,j - 1)。
所以,(i,j)位置的路径总数应该是(i - 1,j)和(i,j - 1)两个位置路径总数之和。
所以,dp[i][j] = dp[i - 1][j] + dp[i][j -1]。
初始化:
由于第一行和第一列中的元素,只能由自己的前一个位置到达,所以它们所对应的 dp 表中的值应该是 1。
确定填表顺序:
根据状态转移方程可以看出应该从二维数组的左上角到右下角依次填入数据。
确定返回值:
题目要求返回到达(m,n)的所有路径总数,所以应该返回 dp[m - 1][n - 1]。
代码:
class Solution
{
public:int uniquePaths(int m, int n) {// 创建 dp 表vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1; // 填表for (int i = 1; i < m; i++){for (int j = 1; j < n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};力扣 63. 不同路径(二)
力扣 63. 不同路径(二)
这道题跟上面的题唯一的不同在于,需要注意二维数组中存在障碍物的位置。
原理还是一样的,只是,如果某一个位置的上边或者左边有障碍物,就不应该再加上这条路径。
其他过程不再赘述。
代码:
class Solution
{
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {if (obstacleGrid[0][0] == 1) return 0;int m = obstacleGrid.size(), n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1) return 0;// 创建 dp 表vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化for (int i = 0; i < m; i++){if (obstacleGrid[i][0] == 0) dp[i][0] = 1;else break;} for (int j = 0; j < n; j++){if (obstacleGrid[0][j] == 0) dp[0][j] = 1;else break;}// 填表for (int i = 1; i < m; i++){for (int j = 1; j < n; j++){// 如果有障碍物, 就不做处理, 保持 0 值if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};力扣 166. 珠宝的最高价值
力扣 166. 珠宝的最高价值
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
其次,由于要记录路径中的每一个位置,所以这道题的 dp 表应该是一个m 行 n 列的二维数组。
每一个位置的含义,也就是 dp[i][j] 指的是,从(0, 0)到 (i,j)可以拿到的珠宝的最高价值之和。
确定状态转移方程:
题目指出,每一次移动只能向下或者向右移动,所以到达(i,j)位置之前的一个位置一定是(i - 1,j)或者(i,j - 1)。
所以,(i,j)位置的最大价值应该是(i - 1,j)和(i,j - 1)两个位置中的最大价值和(i,j)位置本身的价值之和。
所以,dp[i][j] = max(dp[i - 1][j] + dp[i][j -1]) + frame[i][j]。
初始化:
由于第一行和第一列中的元素,只能由自己的前一个位置到达,所以它们所对应的 dp 表中的值应该是本身的价值加上前一个位置的最大价值。
确定填表顺序:
根据状态转移方程可以看出应该从二维数组的左上角到右下角依次填入数据。
确定返回值:
题目要求返回到达右下角时能拿到的珠宝的最大价值,所以应该返回 dp[m - 1][n - 1]。
代码:
class Solution
{
public:int jewelleryValue(vector<vector<int>>& frame) {// 创建 dp 表int m = frame.size(), n = frame[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));// 初始化dp[0][0] = frame[0][0];for (int i = 1; i < m; i++) dp[i][0] = dp[i - 1][0] + frame[i][0];for (int j = 1; j < n; j++) dp[0][j] = dp[0][j - 1] + frame[0][j];// 填表for (int i = 1; i < m; i++){for (int j = 1; j < n; j++){dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];}}return dp[m - 1][n - 1];}
};力扣 931. 下降路径最小和
力扣 931. 下降路径最小和
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
其次,这道题目的 “结尾” 指的是最后一行,而不是右下角。
dp[i][j] 指的是 从第一行到(i,j)位置路径上所有点相加的最小值。
确定状态转移方程:
由题目可得,到达(i,j)位置之前的一个位置一定是(i - 1,j)或者(i - 1,j - 1)或者(i - 1,j + 1)。
所以,(i,j)位置的最小路径和应该是(i - 1,j)(i - 1,j - 1)以及(i - 1,j + 1)三个位置中的最小值和(i,j)位置本身的值相加
所以,dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j -1], dp[i - 1][j + 1])) + matrix[i][j]。
初始化:
这道题可以直接用 matrix 二维数组来初始化 dp 表,后续可以直接在此基础上更改。
确定填表顺序:
根据状态转移方程可以看出应该从上往下每一行依次填入数据。
确定返回值:
题目要求返回到达最后一行的路径上和的最小值,所以应该返回 dp 表中最后一行中的最小值。
代码:
class Solution
{
public:int minFallingPathSum(vector<vector<int>>& matrix) {// 创建 dp 表 + 初始化vector<vector<int>> dp(matrix);// 填表int n = matrix.size();for (int i = 1; i < n; i++){for (int j = 0; j < n; j++){if (j == 0)dp[i][j] += min(dp[i - 1][0], dp[i - 1][1]);else if (j == n-1)dp[i][j] += min(dp[i - 1][n - 1], dp[i - 1][n - 2]);else{int Min = min(dp[i - 1][j - 1], dp[i - 1][j]);dp[i][j] += min(Min, dp[i - 1][j + 1]);}}}int min = dp[n - 1][0];for (int i = 1; i < n; i++)min = dp[n - 1][i] < min ? dp[n - 1][i] : min;return min;}
};力扣 64. 最小路径和
力扣 64. 最小路径和
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
首先,根据写题经验,先确定出这道题应该使用的解题思路是 “以某一个位置为结尾进行分析”。
其次,由于要记录路径中的每一个位置,所以这道题的 dp 表应该是一个m 行 n 列的二维数组。
每一个位置的含义,也就是 dp[i][j] 指的是,从(0, 0)到 (i,j)所有路径中的最小和。
确定状态转移方程:
题目指出,每一次移动只能向下或者向右移动,所以到达(i,j)位置之前的一个位置一定是(i - 1,j)或者(i,j - 1)。
所以,(i,j)位置的最小路径和应该是(i - 1,j)和(i,j - 1)两个位置中的最小值和(i,j)位置本身的值之和。
所以,dp[i][j] = min(dp[i - 1][j] , dp[i][j -1]) + grid[i][j]。
初始化:
这道题可以按照先开一个二维数组,再初始化第一行和第一列的方法初始化。
但是,也可以直接用题目给出的原数组初始化,虽然后续还是要对第一行和第一列进行改动。
各位看自己心情选择吧。
确定填表顺序:
根据状态转移方程可以看出应该从二维数组的左上角到右下角依次填入数据。
确定返回值:
题目要求返回到达右下角的所有路径和中的最小值,所以应该返回 dp[m - 1][n - 1]。
代码:
class Solution
{
public:int minPathSum(vector<vector<int>>& grid) {// 创建 dp 表int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(grid);// 初始化for (int i = 1; i < m; i++) dp[i][0] += dp[i - 1][0];for (int j = 1; j < n; j++) dp[0][j] += dp[0][j - 1];// 填表for (int i = 1; i < m; i++){for (int j = 1; j < n; j++){dp[i][j] += min(dp[i - 1][j], dp[i][j - 1]);}}return dp[m - 1][n - 1];}
};力扣 174. 地下城游戏
力扣 174. 地下城游戏
这道题就有点不一样了,它不能用 “以某一个位置为结尾进行分析”。
解题步骤:
创建 dp 表以及确定 dp 表中所要填写位置的含义:
如果还是以某一个位置为结尾进行分析,则 dp[i][j] 表示从七点到达(i,j)位置所需的最低健康点数,这时虽然知道了 dp[i -1][j] 和 dp[i][j - 1],但是就算可以保证骑士可以到达(i,j),但是能不能到达最后还受后面数字的影响,所以这个方法行不通。
如果以某一个位置为起点进行分析,则 dp[i][j] 表示骑士从(i,j)位置到最后所需的最低健康点数,这时可以从右下角开始。
确定状态转移方程:
dp[i][j] 表示从 i, j 位置出发到达终点所需的最小的健康点数
往右边走:则该位置的健康点数减去该位置消耗的健康点数应该大于等于右边位置所需的健康点数
dp[i][j] + dungeon[i][j] >= dp[i][j + 1] -> dp[i][j] >= dp[i][j + 1] - dungeon[i][j]
往下边走:则该位置的健康点数减去该位置消耗的健康点数应该大于等于下边位置所需的健康点数
dp[i][j] + dungeon[i][j] >= dp[i + 1][j] -> dp[i][j] >= dp[i + 1][j] - dungeon[i][j]
所以,dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
初始化:
这道题我用的方法是,先开一个二维数组,然后初始化最后一行和最后一列。
当然如果你有更喜欢的方法也可以。
各位看自己心情选择吧。
确定填表顺序:
根据状态转移方程可以看出应该从二维数组的右下角到左上角依次填入数据。
确定返回值:
题目要求求出从起点能顺利到达右下角所需的最低健康点数,所以应该返回 dp[0][0]。
还有一个需要注意的点:由状态转移方程可以看出一个漏洞,如果dungeon[i][j]的值是一个很大的正数则会导致dp[i][j] < 0表明骑士已经死亡, 所以当dp[i][j]为负数时,应将其变为1 dp[i][j] = max(1, dp[i][j])。
代码:
class Solution
{
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {// 创建 dp 表int m = dungeon.size(), n = dungeon[0].size();vector<vector<int>> dp(m, vector<int>(n));// 初始化dp[m - 1][n - 1] = 1 - dungeon[m - 1][n - 1];dp[m - 1][n - 1] = max(1, dp[m - 1][n - 1]);for (int i = m - 2; i >= 0; i--){dp[i][n - 1] = dp[i + 1][n - 1] - dungeon[i][n - 1];dp[i][n - 1] = max(1, dp[i][n - 1]);}for (int j = n - 2; j >= 0; j--){dp[m - 1][j] = dp[m - 1][j + 1] - dungeon[m - 1][j];dp[m - 1][j] = max(1, dp[m - 1][j]);}// 填表for (int i = m - 2; i >= 0; i--){for (int j = n - 2; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = max(1, dp[i][j]);}}return dp[0][0];}
};总结
在我看来,动规问题中的路径问题应该有以下几点值得注意的:
-
开出来的 dp 表中,每一个位置到底代表什么。
-
填表的时候一定要注意在容易越界的地方,进行合适的初始化,初始化的数据一定不能影响后面数据的正确性。
-
到底该 “以某一个位置为结尾” 还是 “以某一个位置为起点” 应该看 dp 表中的某一个位置的值,是否还受后面的值的影响。
相关文章:

动态规划之路径问题
动态规划算法介绍 基本原理和解题步骤 针对于动态规划的题型,一般会借助一个 dp 表,然后确定这个表中应该填入什么内容,最终直接返回表中的某一个位置的元素。 细分可以分为以下几个步骤: 创建 dp 表以及确定 dp 表中所要填写位…...

如何优化你的TikTok短视频账号运营策略?
在运营TikTok账号时,采取正确的策略至关重要,这些策略能够帮助你提升账号的质量和吸引力。 适度使用互粉互赞 避免过度依赖互粉互赞,因为这可能会限制你的内容在更广泛的观众中传播。虽然互粉互赞可以增加曝光,但过度使用可能导…...

mysql的唯一索引和普通索引有什么区别
在MySQL中,唯一索引(UNIQUE Index)和普通索引(普通索引,也称为非唯一索引)有一些关键的区别。以下是它们的比较以及性能分析: 唯一索引与普通索引的区别 唯一性: 唯一索引ÿ…...

Scrapy框架在处理大规模数据抓取时有哪些优化技巧?
在使用Scrapy框架处理大规模数据抓取时,优化技巧至关重要,可以显著提高爬虫的性能和效率。以下是一些实用的优化技巧: 1. 并发请求 增加并发请求的数量可以提高爬虫的响应速度和数据抓取效率。可以通过设置CONCURRENT_REQUESTS参数来调整。…...

私有化低代码平台的优势:赋能业务用户,重塑IT自主权
随着数字化转型在全球范围内的不断推进,企业面临着快速响应市场变化和提高内部运营效率的双重挑战。在这种背景下,低代码平台逐渐成为企业实现敏捷开发和快速迭代的重要工具。私有化低代码平台作为一种更安全、可控的解决方案,越来越受到企业…...

SAP BW系统表分享第一弹
有时候想要查看BW系统中存在了多少的表时,包含SAP以及自建表,这个时候我们怎么去找呢? 不要慌,BW系统中也有其对应系统表来存储表对应的信息的,存储所有表信息的是DD02V或者DD02VV,我比较推荐使用DD02VV&a…...

详解工厂模式与抽象工厂模式有什么区别?【图解+代码】
目录 工厂模式,抽象工厂模式是什么? 两种设计模式的流程: 1、工厂模式 2、抽象工厂模式 两种模式的对比 共同点: 不同点: 总结 工厂模式,抽象工厂模式是什么? 我已经具体的写了这两种模…...

zeroice做json字符串转为struct,支持结构体嵌套
1 zeroice Properties 基础类型 字典 数组 不支持复杂结构 2 zeroice没有内置反射 3 java反射 slice2java.exe ice转java类 java类转json字符串 json字符串组织测试json文件 jsonobj转为vector jar包onjvm运行 pub到broker 4 c反射from_json.cpp slice2cpp.exe ice转.h 注…...

Linux笔记 --- 内存管理
在程序中我们访问的内存地址都是从物理内存上映射而来的虚拟地址,假设我们使用的计算机实际物理内存(PM)只有1GB,而Linux中执行着三个进程,Linux会将PM中的某段内存映射成三段4G大小相同的虚拟内存(VM&…...

树莓派通过webRTC进行视频流传输到公网
为了实现树莓派和浏览器之间的视频流传输,你需要在公网服务器上运行 Node.js 的信令服务器,同时在树莓派上运行 Node.js 客户端代码。以下是具体的步骤和说明: 1. 公网服务器 安装 Node.js:在公网服务器上,你需要安装…...

【数据结构与算法】循环队列
循环队列 一.循环队列的引入二.循环队列的原理三.循环队列判断是否为满或空1.是否为空2.是否为满 四.循环队列入队五.循环队列出队六.循环队列的遍历七.循环队列获取长度八.总结 一.循环队列的引入 还记得我们顺序队列的删除元素嘛,我们有两种方式,一种是将数组要删除元素后面…...

为什么推荐使用@RequiredArgsConstructor代替@Autowired?
首先说一下前提: 项目中已经使用了Lombok,否则添加 Lombok 可能会增加项目的复杂度和构建时间。如果依赖项是可选的或可能在运行时改变,则使用字段注入或 setter 注入可能更为合适。 正文: 在 Spring 框架中,Autowir…...

ARM系列运行异常排查
一、断点指令BKPT BKPT指令产生软件断点中断,可用于程序的调试。它使处理器停止执行正常指令(使处理器中止预取指)而进入相应的调试程序。 BKPT指令的格式为:BKPT 16位的立即数 二、使用BKPT进行软件异常定位 假设异常发生后…...

Hive3:库操作常用语句
1、创建库 create database if not exists myhive;2、选择库 use myhive;3、查看当前选择的库 SELECT current_database();4、查看库详细信息 desc database myhive;可以查看数据文件在hdfs集群中的存储位置 5、创建库时制定hdfs的存储位置 create database myhive2 …...

C语言实现:C51单片机驱动LCD屏幕显示字符串(Proteus+Keil)
在Proteus中绘制电路原理图 我使用的版本是Protues8.16 ,Protues特别擅长仿真单片机及其外围设备,支持多种类型的微控制器,如8051、HC11、PIC、AVR、ARM、MSP430等,也可以设计pcb板,还能3D建模 1.新建工程 在 Start 栏中点击 …...

暄桐好作业之《临沈周〈东庄图册〉局部》
暄桐是一间传统美学教育教室,创办于2011年,林曦是创办人和授课老师,教授以书法为主的传统文化和技艺,皆在以书法为起点,亲近中国传统之美,以实践和所得,滋养当下生活。 其中“暄桐好作…...

Qt3D创建3D物体步骤
使用Qt3D接口创建3D物体的步骤大致有以下几步: 1.创建一个3D窗口 2.创建根实体 3.创建物体实体,父指针为根实体 4.创建立体图形,即物体网格,设置物体的属性 5.给立体图形添加材质,添加坐标位置,添加纹理,添加其他效果 6.创建摄像头,设置摄像头的属性,父指针为根…...
UDP程序设计
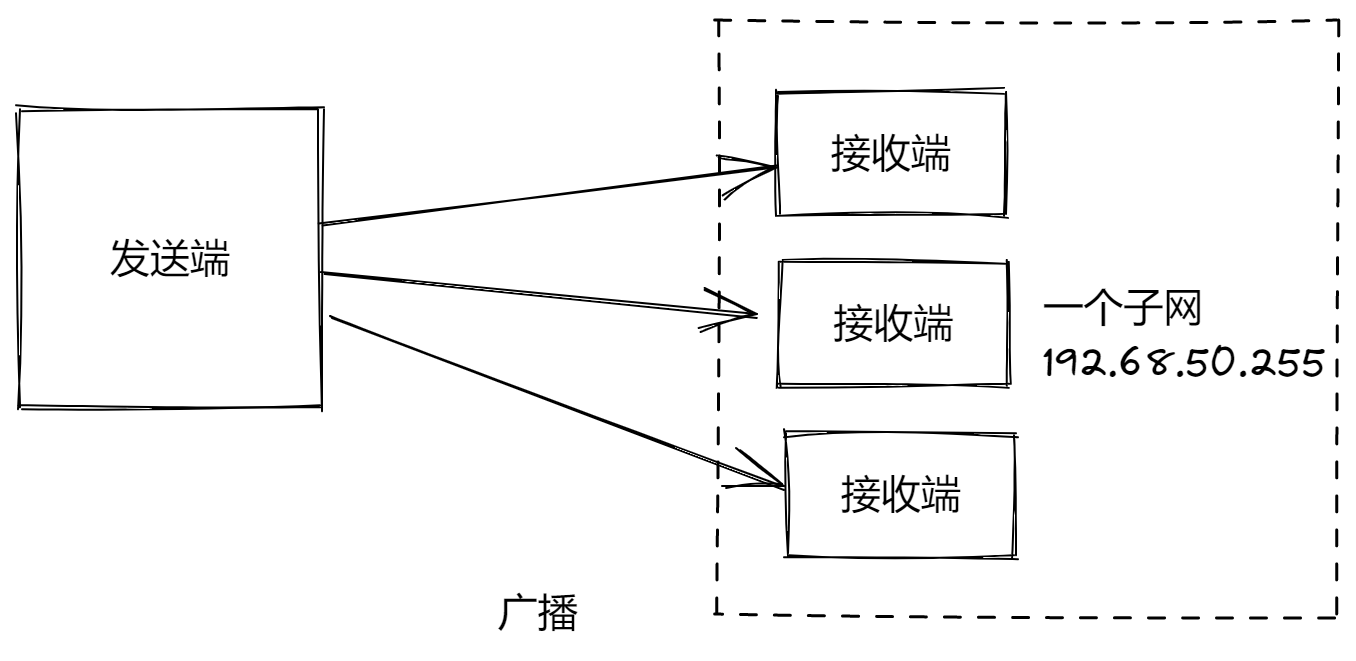
UDP协议概述 UDP,User Datagram Protocol,用户数据报协议,是一个简单的面向数据报(package-oriented)的传输层协议,规范为:RFC 768。 UDP提供数据的不可靠传递,它一旦把应用程序发给网络层的数据发送出去…...

计算机网络—电路、分组、报文交换—图文详解
计算机网络—电路、分组、报文交换 计算机网络中的数据传输方式可以根据数据的处理方式和网络资源的使用方式分为电路交换、分组交换和报文交换三种类型。 这些方式在网络设计和数据传输过程中起到了不同的作用和效果。 1. 电路交换(Circuit Switching࿰…...

linux下交叉编译licensecc
本文章只做个人笔记用 下载地址: #https://github.com/open-license-manager/licensecc.git #下面地址下不下来就是用第一个去官网下载git clone --recursive https://github.com/open-license-manager/licensecc.git 编译前准备3个库:openssl&#x…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
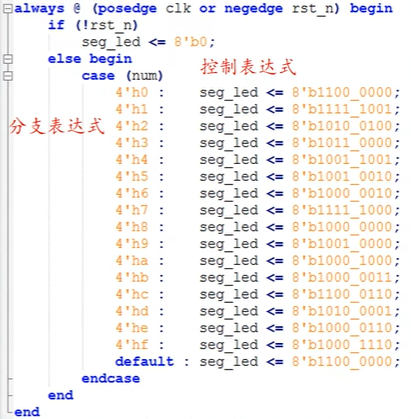
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

大模型的LoRa通讯详解与实现教程
一、LoRa通讯技术概述 LoRa(Long Range)是一种低功耗广域网(LPWAN)通信技术,由Semtech公司开发,特别适合于物联网设备的长距离、低功耗通信需求。LoRa技术基于扩频调制技术,能够在保持低功耗的同时实现数公里甚至数十公里的通信距离。 LoRa的主要特点 长距离通信:在城…...

Ansys Maxwell:线圈和磁体的静磁 3D 分析
本博客展示了如何在 Ansys Maxwell 中执行静磁 3D 分析,以计算载流线圈和永磁体之间相互作用产生的扭矩。在这个例子中,线圈中的电流产生一个沿 Y 轴指向的磁场,而永磁体沿 X 轴被磁化。这种配置导致围绕 Z 轴的扭矩。分步工作流程包括构建几…...

四、Sqoop 导入表数据子集
作者:IvanCodes 日期:2025年6月4日 专栏:Sqoop教程 当不需要将关系型数据库中的整个表一次性导入,而是只需要表中的一部分数据时,Sqoop 提供了多种方式来实现数据子集的导入。这通常通过过滤条件或选择特定列来完成。 …...

PostgreSQL 的扩展pg_freespacemap
PostgreSQL 的扩展pg_freespacemap pg_freespacemap 是 PostgreSQL 提供的一个内置扩展,用于查看表的空闲空间映射(Free Space Map, FSM)信息。这个扩展对于数据库性能调优和空间管理非常有用。 一 扩展概述 功能:提供对表的空…...
