数模原理精解【5】
文章目录
- 二元分布
- 满足要求
- 边际分布
- 条件概率
- 例子1
- 例子2
- 损失函数
- 概率分布
- 期望值
- 例
- 参考文献
二元分布
满足要求
连续情况下, φ ( x , y ) \varphi (x,y) φ(x,y)为随机变量 X 、 Y X、Y X、Y的联合概率分布(二元分布),如果以下条件满足:
1 、 ∀ X 和 Y 值有 0 ≤ φ ( x , y ) ≤ 1 2 、离散型: ∑ y ∑ x φ ( x , y ) = 1 连续型 : ∫ − ∞ + ∞ ∫ − ∞ + ∞ φ ( x , y ) d x d y = 1 1、\forall X和Y值有 0 \le \varphi(x,y) \le 1 \\2、离散型:\sum_y\sum_x \varphi(x,y)=1 \\ 连续型:\textstyle\intop_{-\infty}^{+\infty}\textstyle\intop_{-\infty}^{+\infty}\varphi(x,y)dxdy=1 1、∀X和Y值有0≤φ(x,y)≤12、离散型:y∑x∑φ(x,y)=1连续型:∫−∞+∞∫−∞+∞φ(x,y)dxdy=1
边际分布
- φ ( x , y ) \varphi (x,y) φ(x,y)为随机变量 X 、 Y X、Y X、Y的联合概率分布
离散型: X 边际概率密度: φ X ( x ) = P ( X = x ) = ∑ y P ( X = x , Y = y ) = ∑ y φ ( x , y ) Y 边际概率密度: φ Y ( y ) = P ( Y = y ) = ∑ x P ( X = x , Y = y ) = ∑ x φ ( x , y ) 连续型: X 边际概率密度: φ X ( x ) = ∫ φ ( x , y ) d y Y 边际概率密度: φ Y ( y ) = ∫ φ ( x , y ) d x \begin{aligned} & 离散型:\\ & X边际概率密度:\varphi_X(x)=P(X=x)=\sum_yP(X=x,Y=y)=\sum_y\varphi (x,y)\\ & Y边际概率密度:\varphi_Y(y)=P(Y=y)=\sum_xP(X=x,Y=y)=\sum_x\varphi (x,y)\\ & 连续型:\\ & X边际概率密度:\varphi_X(x)=\intop\varphi(x,y)dy\\ & Y边际概率密度:\varphi_Y(y)=\intop\varphi(x,y)dx\\ \end{aligned} 离散型:X边际概率密度:φX(x)=P(X=x)=y∑P(X=x,Y=y)=y∑φ(x,y)Y边际概率密度:φY(y)=P(Y=y)=x∑P(X=x,Y=y)=x∑φ(x,y)连续型:X边际概率密度:φX(x)=∫φ(x,y)dyY边际概率密度:φY(y)=∫φ(x,y)dx
条件概率
P ( A ∣ B ) = P ( A ⋂ B ) P ( B ) P(A|B)=\frac {P(A\bigcap B)}{P(B)} P(A∣B)=P(B)P(A⋂B)
例子1
设 : P ( 0 , 0 ) = 0.27 , P ( 0 , 1 ) = 0.19 , P ( 0 , 2 ) = 0.24 P ( 1 , 0 ) = 0.1 , P ( 1 , 1 ) = 0.03 , P ( 1 , 2 ) = 0.17 φ ( x , y ) = P ( X = x , Y = y ) 1 、 0 ≤ φ ( x , y ) ≤ 1 2 、 ∑ x ∑ y φ ( x , y ) = 0.27 + 0.19 + 024 + 0.1 + 0.03 + 0.17 = 1 符合离散型二元分布的要求。 一、求 φ X ( 1 ) = P ( X = 1 ) = ? ,此为条件概率分布 P ( X = 1 ) = P ( Y ∣ X = 1 ) = P ( Y ∣ 1 ) = P ( X ⋂ Y ) P ( X ) = P ( 1 , Y ) P ( 1 ) = P ( 1 , Y ) P ( 1 , 0 ) + P ( 1 , 1 ) + P ( 1 , 2 ) = P ( 1 , Y ) 0.1 + 0.03 + 0.17 = P ( 1 , Y ) 0.3 P ( Y = 2 , X = 1 ) = P ( Y = 2 ∣ 1 ) = P ( 2 ∣ 1 ) = P ( 1 , 2 ) 0.3 = 0.17 0.3 = 0.56 二、边际概率分布 Y 边际概率密度: φ Y ( 2 ) = P ( Y = y ) = P ( Y = 2 ) = ∑ x P ( X = x , Y = 2 ) = ∑ x P ( x , 2 ) = 0.24 + 0.17 = 0.41 设: \\P(0,0)=0.27,P(0,1)=0.19,P(0,2)=0.24 \\P(1,0)=0.1,P(1,1)=0.03,P(1,2)=0.17 \\\varphi (x,y)=P(X=x,Y=y) \\1、0\le \varphi (x,y) \le 1 \\2、\sum_x\sum_y\varphi (x,y)=0.27+0.19+024+0.1+0.03+0.17=1 \\符合离散型二元分布的要求。 \\一、求\varphi_X(1)=P(X=1)=? ,此为条件概率分布 \\P(X=1)=P(Y|X=1)=P(Y|1)=\frac {P(X\bigcap Y)} {P(X)}=\frac {P(1,Y)} {P(1)}=\frac {P(1,Y)} {P(1,0)+P(1,1)+P(1,2)} \\=\frac {P(1,Y)} {0.1+0.03+0.17}=\frac {P(1,Y)} {0.3} \\P(Y=2,X=1)=P(Y=2|1)=P(2|1)=\frac {P(1,2)} {0.3}=\frac {0.17} {0.3}=0.56 \\二、边际概率分布 \\Y边际概率密度:\varphi_Y(2)=P(Y=y)=P(Y=2) \\=\sum_xP(X=x,Y=2)=\sum_xP(x,2)\\=0.24+0.17=0.41 设:P(0,0)=0.27,P(0,1)=0.19,P(0,2)=0.24P(1,0)=0.1,P(1,1)=0.03,P(1,2)=0.17φ(x,y)=P(X=x,Y=y)1、0≤φ(x,y)≤12、x∑y∑φ(x,y)=0.27+0.19+024+0.1+0.03+0.17=1符合离散型二元分布的要求。一、求φX(1)=P(X=1)=?,此为条件概率分布P(X=1)=P(Y∣X=1)=P(Y∣1)=P(X)P(X⋂Y)=P(1)P(1,Y)=P(1,0)+P(1,1)+P(1,2)P(1,Y)=0.1+0.03+0.17P(1,Y)=0.3P(1,Y)P(Y=2,X=1)=P(Y=2∣1)=P(2∣1)=0.3P(1,2)=0.30.17=0.56二、边际概率分布Y边际概率密度:φY(2)=P(Y=y)=P(Y=2)=x∑P(X=x,Y=2)=x∑P(x,2)=0.24+0.17=0.41
例子2
对于 φ ( x , y ) = P ( a x ≤ X ≤ b x , a y ≤ Y ≤ b y ) = ∫ a x b x ∫ a y b y φ ( x , y ) d x d y 1 、 ∀ X 和 Y 值有 0 ≤ φ ( x , y ) ≤ 1 2 、连续型 : ∫ − ∞ + ∞ ∫ − ∞ + ∞ φ ( x , y ) d x d y = 1 符合连续型二元分布的要求。 设 : a x = 0 , b x = 1 , a y = 0 , b y = 1 φ ( x , y ) = { 3 x + 5 y 2 if 0 ≤ X ≤ 1 , 0 ≤ Y ≤ 1 0 if e l s e 一、求边际概率分布 φ X ( x ) = ? φ X ( x ) = ∫ φ ( x , y ) d y = ∫ 0 1 φ ( x , y ) d y = ∫ 0 1 ( 3 x + 5 y 2 ) d y = 3 x + 5 ∫ 0 1 y 2 d y = 3 x + 5 3 y 3 ∣ 0 1 = 3 x + 5 3 φ Y ( y ) = ? φ Y ( y ) = ∫ φ ( x , y ) d x = ∫ 0 1 φ ( x , y ) d x = ∫ 0 1 ( 3 x + 5 y 2 ) d x = 3 2 x 2 ∣ 0 1 + 5 y 2 = 3 2 + 5 y 2 给定任意 y 值: φ Y ( 0.5 ) = 3 2 + 5 ∗ 0. 5 2 φ Y ( − 1 ) = 0 二、求条件概率分布 φ X ∣ Y ( x ∣ y ) = P ( X = x , Y = y ) P ( Y = y ) = φ X , Y ( x , y ) φ Y ( y ) φ Y ∣ X ( y ∣ x ) = P ( Y = y , X = x ) P ( X = x ) = φ X , Y ( x , y ) φ X ( x ) φ X ∣ Y ( x ∣ y ) = φ X , Y ( x , y ) φ Y ( y ) = 3 x + 5 y 2 3 2 + 5 y 2 φ Y ∣ X ( y ∣ x ) = φ X , Y ( x , y ) φ X ( x ) = 3 x + 5 y 2 3 x + 5 3 设 y = 0.7 , x ≤ 1 3 φ X ∣ Y ( X ≤ 1 3 , Y = 0.7 ) = P ( X ≤ 1 3 , X = 0.7 ) = ∫ 0 1 3 φ X ∣ Y ( x ∣ 0.7 ) d x = ∫ 0 1 3 3 x + 5 ∗ ( 0.7 ) 2 3 2 + 5 ∗ ( 0.7 ) 2 d x = . . . . . 设 x = 0.7 , y ≤ 1 3 φ Y ∣ X ( Y ≤ 1 3 , X = 0.7 ) = P ( X ≤ 1 3 , X = 0.7 ) = ∫ 0 1 3 φ Y ∣ X ( y ∣ 0.7 ) d x = ∫ 0 1 3 3 ∗ 0.7 + 5 y 2 3 ∗ 0.7 + 5 3 d y = . . . 对于\\\varphi (x,y)=P(a_x\le X\le b_x,a_y \le Y \le b_y)=\textstyle\intop_{a_x}^{b_x}\intop_{a_y}^{b_y}\varphi(x,y)dxdy \\1、\forall X和Y值有 0 \le \varphi(x,y) \le 1 \\2、连续型:\textstyle\intop_{-\infty}^{+\infty}\textstyle\intop_{-\infty}^{+\infty}\varphi(x,y)dxdy=1 \\符合连续型二元分布的要求。 \\设:a_x=0,b_x=1,a_y=0,b_y=1 \\\varphi(x,y)=\begin{cases} 3x+5y^2 &\text{if } 0 \le X \le 1,0 \le Y\le 1 \\ 0 &\text{if } else \end{cases} \\一、求边际概率分布 \\\varphi_X(x)=? \\\varphi_X(x)=\intop\varphi(x,y)dy\\ \\=\intop_{0}^{1}\varphi(x,y)dy=\intop_{0}^{1}(3x+5y^2)dy=3x+5\intop_{0}^{1}y^2dy=3x+\frac 5 3 {y^3}|_{0}^{1}=3x+\frac 5 3 \\\varphi_Y(y)=? \\\varphi_Y(y)=\intop\varphi(x,y)dx\\ \\=\intop_{0}^{1}\varphi(x,y)dx=\intop_{0}^{1}(3x+5y^2)dx=\frac 3 2 x^2|_0^1+5y^2=\frac 3 2+5y^2 \\给定任意y值: \\\varphi_Y(0.5)=\frac 3 2+5*0.5^2 \\\varphi_Y(-1)=0 \\二、求条件概率分布\\ \begin{aligned} & \varphi_{X|Y}(x|y)=\frac {P(X=x,Y=y)} {P(Y=y)}=\frac {\varphi_{X,Y}(x,y)}{\varphi_Y(y)} \\ &\varphi_{Y|X}(y|x)=\frac {P(Y=y,X=x)} {P(X=x)}=\frac {\varphi_{X,Y}(x,y)}{\varphi_X(x)}\\ \end{aligned} \\ \varphi_{X|Y}(x|y)=\frac {\varphi_{X,Y}(x,y)}{\varphi_Y(y)} =\frac {3x+5y^2} {\frac 3 2+5y^2} \\ \varphi_{Y|X}(y|x)=\frac {\varphi_{X,Y}(x,y)}{\varphi_X(x)} =\frac {3x+5y^2} {3x+\frac 5 3} \\设y=0.7,x \le \frac 1 3 \\\varphi_{X|Y}(X \le \frac 1 3,Y=0.7)=P(X \le \frac 1 3,X=0.7)=\intop_0^{\frac 1 3}\varphi_{X|Y}(x|0.7)dx=\intop_0^{\frac 1 3}\frac {3x+5*(0.7)^2} {\frac 3 2+5*(0.7)^2}dx=..... \\设x=0.7,y \le \frac 1 3 \\\varphi_{Y|X}(Y \le \frac 1 3,X=0.7)=P(X \le \frac 1 3,X=0.7)=\intop_0^{\frac 1 3}\varphi_{Y|X}(y|0.7)dx=\intop_0^{\frac 1 3}\frac {3*0.7+5y^2} {3*0.7+\frac 5 3}dy=... 对于φ(x,y)=P(ax≤X≤bx,ay≤Y≤by)=∫axbx∫aybyφ(x,y)dxdy1、∀X和Y值有0≤φ(x,y)≤12、连续型:∫−∞+∞∫−∞+∞φ(x,y)dxdy=1符合连续型二元分布的要求。设:ax=0,bx=1,ay=0,by=1φ(x,y)={3x+5y20if 0≤X≤1,0≤Y≤1if else一、求边际概率分布φX(x)=?φX(x)=∫φ(x,y)dy=∫01φ(x,y)dy=∫01(3x+5y2)dy=3x+5∫01y2dy=3x+35y3∣01=3x+35φY(y)=?φY(y)=∫φ(x,y)dx=∫01φ(x,y)dx=∫01(3x+5y2)dx=23x2∣01+5y2=23+5y2给定任意y值:φY(0.5)=23+5∗0.52φY(−1)=0二、求条件概率分布φX∣Y(x∣y)=P(Y=y)P(X=x,Y=y)=φY(y)φX,Y(x,y)φY∣X(y∣x)=P(X=x)P(Y=y,X=x)=φX(x)φX,Y(x,y)φX∣Y(x∣y)=φY(y)φX,Y(x,y)=23+5y23x+5y2φY∣X(y∣x)=φX(x)φX,Y(x,y)=3x+353x+5y2设y=0.7,x≤31φX∣Y(X≤31,Y=0.7)=P(X≤31,X=0.7)=∫031φX∣Y(x∣0.7)dx=∫03123+5∗(0.7)23x+5∗(0.7)2dx=.....设x=0.7,y≤31φY∣X(Y≤31,X=0.7)=P(X≤31,X=0.7)=∫031φY∣X(y∣0.7)dx=∫0313∗0.7+353∗0.7+5y2dy=...
损失函数
L ( c 1 , a 1 ) 为损失函数 其中, a 1 为事件, c 1 为自然状态的真值。 ( c 1 , a 1 ) ∈ C ∗ A c 为参数,属于参数空间 C a 为行为(事件),属于所有可能的事件集合 A L(c_1,a_1)为损失函数 \\其中,a_1为事件,c_1为自然状态的真值。 \\(c_1,a_1) \in C*A \\c为参数,属于参数空间C \\a为行为(事件),属于所有可能的事件集合A L(c1,a1)为损失函数其中,a1为事件,c1为自然状态的真值。(c1,a1)∈C∗Ac为参数,属于参数空间Ca为行为(事件),属于所有可能的事件集合A
概率分布
- 调查结果为随机变量 X = ( x 1 , x 2 , . . . , x n ) X=(x_1,x_2,...,x_n) X=(x1,x2,...,xn), x i x_i xi为同一分布的独立观测值,发生的自然状态是 c c c(可理解为给定条件), P c ( A ) P_c(A) Pc(A)为事件A在自然状态c发生时出现的概率, φ \varphi φ为概率函数,即随机事件到其发生概率的映射。
- Φ 为样本空间集合,其元素为某随机变量 X ( X ∈ Φ ) , X 包括很多事件 x 1 , x 2 . . . . , x n \Phi为样本空间集合,其元素为某随机变量X(X \in \Phi),X包括很多事件x_1,x_2....,x_n Φ为样本空间集合,其元素为某随机变量X(X∈Φ),X包括很多事件x1,x2....,xn
- 连续
P c ( A ) = ∫ A φ ( x ∣ c ) d x P_c(A)=\intop_A\varphi(x|c)dx Pc(A)=A∫φ(x∣c)dx
-离散
P c ( A ) = ∑ x ∈ A φ ( x ∣ c ) P_c(A)=\sum_{x \in A}\varphi(x|c) Pc(A)=x∈A∑φ(x∣c)
期望值
μ ( x ) 为对 X 的数学期望,给定条件 c 值。 E c [ μ ( x ) ] = ∫ Φ μ ( x ) φ ( x ∣ c ) d x = ∑ x ∈ Φ μ ( x ) φ ( x ∣ c ) \mu(x)为对X的数学期望,给定条件c值。 \\E_c[\mu(x)]=\int_\Phi\mu(x)\varphi(x|c)dx \\=\sum_{x \in \Phi}\mu(x)\varphi(x|c) μ(x)为对X的数学期望,给定条件c值。Ec[μ(x)]=∫Φμ(x)φ(x∣c)dx=x∈Φ∑μ(x)φ(x∣c)
例
1、设一个产品所需要的某原材料可用两种材料之一,这两种材料分别被A方和B方提供。
产品选择原材料导致产品使用寿命损失函数为:
L ( c , a 1 ) = ∣ 5 c 2 + 7 c ∣ L ( c , a 2 ) = ∣ 2 c + 8 c 2 ∣ 其中, a 2 表示产品所需原材料被 B 方提供, a 1 表示产品所需要原材料被 A 方提供, c 表示该材料的强度耐受度。 L(c,a_1)=|5c^2+7c| \\L(c,a_2)=|2c+8c^2| \\其中,a_2表示产品所需原材料被B方提供,a_1表示产品所需要原材料被A方提供,c表示该材料的强度耐受度。 \\ \\ L(c,a1)=∣5c2+7c∣L(c,a2)=∣2c+8c2∣其中,a2表示产品所需原材料被B方提供,a1表示产品所需要原材料被A方提供,c表示该材料的强度耐受度。
2、将二百万人民币投资某项目,或存入基金,其损失函数(单位:万元,负数表示收益)为:
设 a 1 表示投资某项目, a 2 表示存入基金, c 1 表示取得预期收益, c 2 表示没有取得预期收益。 L ( a 1 , c 1 ) = − 9 L ( a 1 , c 2 ) = 7 L ( a 2 , c 1 ) = − 28 L ( a 2 , c 2 ) = 50 设a_1表示投资某项目,a_2表示存入基金,c_1表示取得预期收益,c_2表示没有取得预期收益。 \\L(a_1,c_1)=-9 \\L(a_1,c_2)=7 \\L(a_2,c_1)=-28 \\L(a_2,c_2)=50 设a1表示投资某项目,a2表示存入基金,c1表示取得预期收益,c2表示没有取得预期收益。L(a1,c1)=−9L(a1,c2)=7L(a2,c1)=−28L(a2,c2)=50
损失矩阵如下:
| a-c | c1 | c2 |
|---|---|---|
| a1 | -9 | 7 |
| a2 | -28 | 50 |
参考文献
1、《统计决策理论与贝叶斯分析》
2. 《统计学(原书第五版)》
相关文章:

数模原理精解【5】
文章目录 二元分布满足要求边际分布条件概率例子1例子2 损失函数概率分布期望值例 参考文献 二元分布 满足要求 连续情况下, φ ( x , y ) \varphi (x,y) φ(x,y)为随机变量 X 、 Y X、Y X、Y的联合概率分布(二元分布),如果以下条件满足: …...

C语言篇——使用运算符将16进制数据反转
比如:将一个16进制0xFD,即11111101,反向,输出10111111,即0xBF。 #include <stdio.h>unsigned char reverseBits(unsigned char num) {unsigned char reverse_num 0;int i;for (i 0; i < 8; i) {if ((num &…...
)
2025年和2024CFA一级SchweserKaplan Notes 全集 (内附分享链接)
CFA一级notes百度网盘下载 2024年和2025年 CFA一级考纲已经正式发布,相比与老考纲,新考纲变化实在不算小。 2024年和2025年 CFA一级notes完整版全 https://drive.uc.cn/s/6394c0b6b1a54?public1 2024年和2025年 cfa二级notes完整版全 https://driv…...

B树的实现:代码示例与解析
B树的实现:代码示例与解析 引言 B树是一种自平衡的树数据结构,广泛应用于文件系统和数据库系统中。它是一种多路搜索树,旨在保持数据有序并允许高效的查找、插入和删除操作。本文将深入探讨B树的实现,提供完整的代码示例和详细的…...

HCIA总结
一、情景再现:ISP网络为学校提供了DNS服务,所以,DNS服务器驻留在ISP网络内,而不再学校网络内。DHCP服务器运行在学校网络的路由器上 小明拿了一台电脑,通过网线,接入到校园网内部。其目的是为了访问谷歌网站…...

软件测试_接口测试面试题
接口测试是软件测试中的重要环节,它主要验证系统不同模块之间的通信和数据交互是否正常。在软件开发过程中,各个模块之间的接口是实现功能的关键要素,因此对接口进行全面而准确的测试是确保系统稳定性和可靠性的关键步骤。 接口测试的核心目…...
)
C++初阶学习第五弹——类与对象(下)
类与对象(上):C初阶学习第三弹——类与对象(上)-CSDN博客 类和对象(中):C初阶学习第四弹——类与对象(中)-CSDN博客 一.赋值运算符重载 1.1 运算符重载 C为…...

最低工资标准数据(2001-2023年不等)、省市县,整理好的面板数据(excel格式)
时间范围:2001-2022年 具体内容:一:最低工资数据标准时间:2012-2021包含指标: 省份城市/区县小时最低工资标准(非全日制)月最低工资标准实施日期 样例数据: 二:各省最低…...

计算机毕业设计选题推荐-戏曲文化体验系统-Java/Python项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

【深度学习】CosyVoice,论文
CosyVoice_v1.pdf 文章目录 CosyVoice: A Scalable Multilingual Zero-shot Text-to-speech Synthesizer based on Supervised Semantic Tokens摘要1 引言2 CosyVoice: 使用监督语义标记的可扩展TTS模型2.1 用于语音的监督语义标记2.2 用于TTS的大型语言模型2.3 最优传输条件流…...
PHP8.3.9安装记录,Phpmyadmin访问提示缺少mysqli
ubuntu 22.0.4 腾讯云主机 下载好依赖 sudo apt update sudo apt install -y build-essential libxml2-dev libssl-dev libcurl4-openssl-dev pkg-config libbz2-dev libreadline-dev libicu-dev libsqlite3-dev libwebp-dev 下载php8.3.9安装包 nullhttps://www.php.net/d…...

[译] 深入浅出Rust基金会
本篇是对 RustConf 2023中的Rust Foundation: Demystified这一视频的翻译与整理, 过程中为符合中文惯用表达有适当删改, 版权归原作者所有. 大家好,我是Sage Griffin,我的代词是they/them。我今天来这里是要谈谈Rust基金会。 要了解基金会实际做什么,我们需要理解美国国内税收…...

Postman:API开发与测试的强大伴侣
在当今的数字化时代,API(应用程序编程接口)已成为不同软件系统之间通信的桥梁,它们如同数字世界的“翻译官”,使得数据和服务能够在不同的平台和应用程序之间无缝流动。然而,API的开发、测试和维护并非易事…...

Web应用的视界革命:WebKit支持屏幕方向API的深度解析
Web应用的视界革命:WebKit支持屏幕方向API的深度解析 在现代Web应用开发中,屏幕方向的适应性是一个重要的考虑因素。屏幕方向API(Screen Orientation API)提供了一种方法,允许Web应用知道并响应屏幕的方向变化&#x…...

【前端】一文带你了解 CSS
文章目录 1. CSS 是什么2. CSS 引入方式2.1 内部样式2.2 外部样式2.3 内联样式 3. CSS 常见选择器3.1 基础选择器3.1.1 标签选择器3.1.2 类选择器3.1.3 id 选择器3.1.4 通配符选择器 3.2 复合选择器3.2.1 后代选择器 4. CSS 常用属性4.1 字体相关4.2 文本相关4.3 背景相关4.4 设…...

IT服务运营管理中的关键考核指标
IT服务运营过程中常见的关键考核指标体现在人员、技术、资源、过程、质量等要素中,下面把常见的考核项目、计算方式、考核周期罗列如下,本考核指标主要用于对IT服务运营单位或部门的考核。 IT服务运营管理关键考核指标 要素考核项目计算方式常见考核周期…...

如何恢复硬盘里删除的数据?硬盘数据恢复真的可靠吗?2024最新解答!
在日常的计算机使用中,我们时常会不小心删除硬盘中的重要数据,这时候,数据恢复就显得尤为重要。本文将介绍几种恢复硬盘里删除数据的方法,并探讨硬盘数据恢复的可靠性,提供2024年的最新解答。 一、什么是电脑硬盘&…...

Android Studio的新界面,怎么切换回老界面
将勾选的 Enable new UI 取消掉即可...
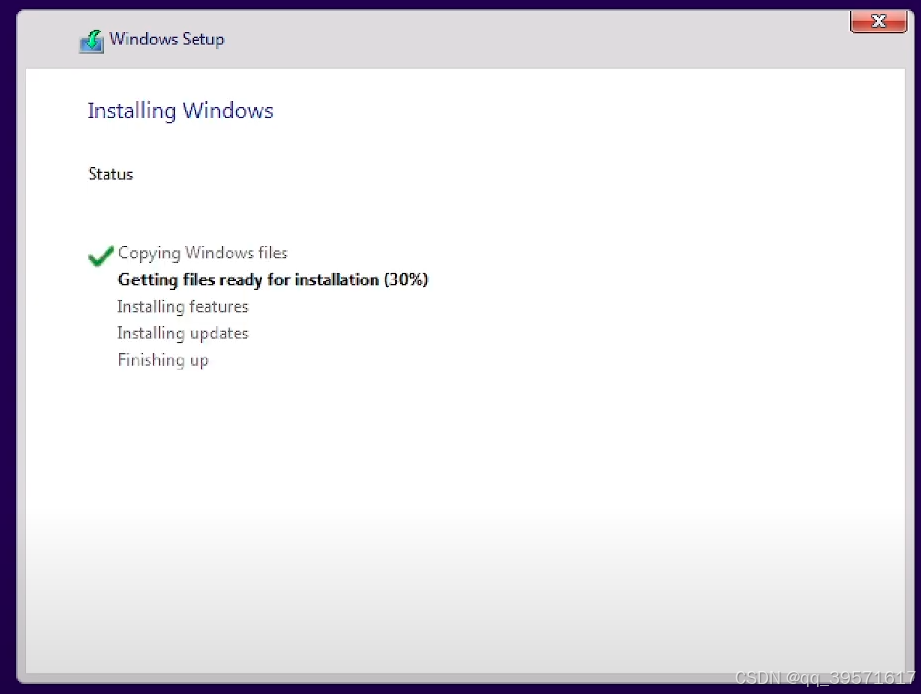
怎么用U盘重装系统
在使用电脑的过程中,难免会遇到系统故障、运行缓慢等问题。当这些问题严重影响使用电脑的体验时,重装系统往往是一个有效的解决办法。用U盘重装系统是一种简单快捷的方法,本文将详细介绍如何使用U盘来重装系统,帮助大家轻松完成这…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

