链式栈，队列与树形结构

链式栈

链式存储的栈

实现方式：可以使用单向链表完成

对单向链表进行头插（入栈）、头删（出栈），此时链表的头部就是链栈的栈顶，链表的尾部，就是链栈的栈底

队列

概念

队列：操作受限的线性表，插入和删除只能在异端操作

队列的特点：先进先出（FIFO），后进后出（LILO

队头：可以进行删除的一段

队尾：可以进行插入的一段

队列的种类：顺序队列，链式队列

顺序队列

顺序存储的队列（保证存储的数据逻辑上相邻，物理内存上也相连，还要保证符合队列的特点）

顺序队列的组成

需要一片连续的空间存放数据（数组，堆区的一片连续的空间）

需要一个变量记录队头的位置

需要一个变量记录队尾的位置（最后一个元素的下一个元素的位置）

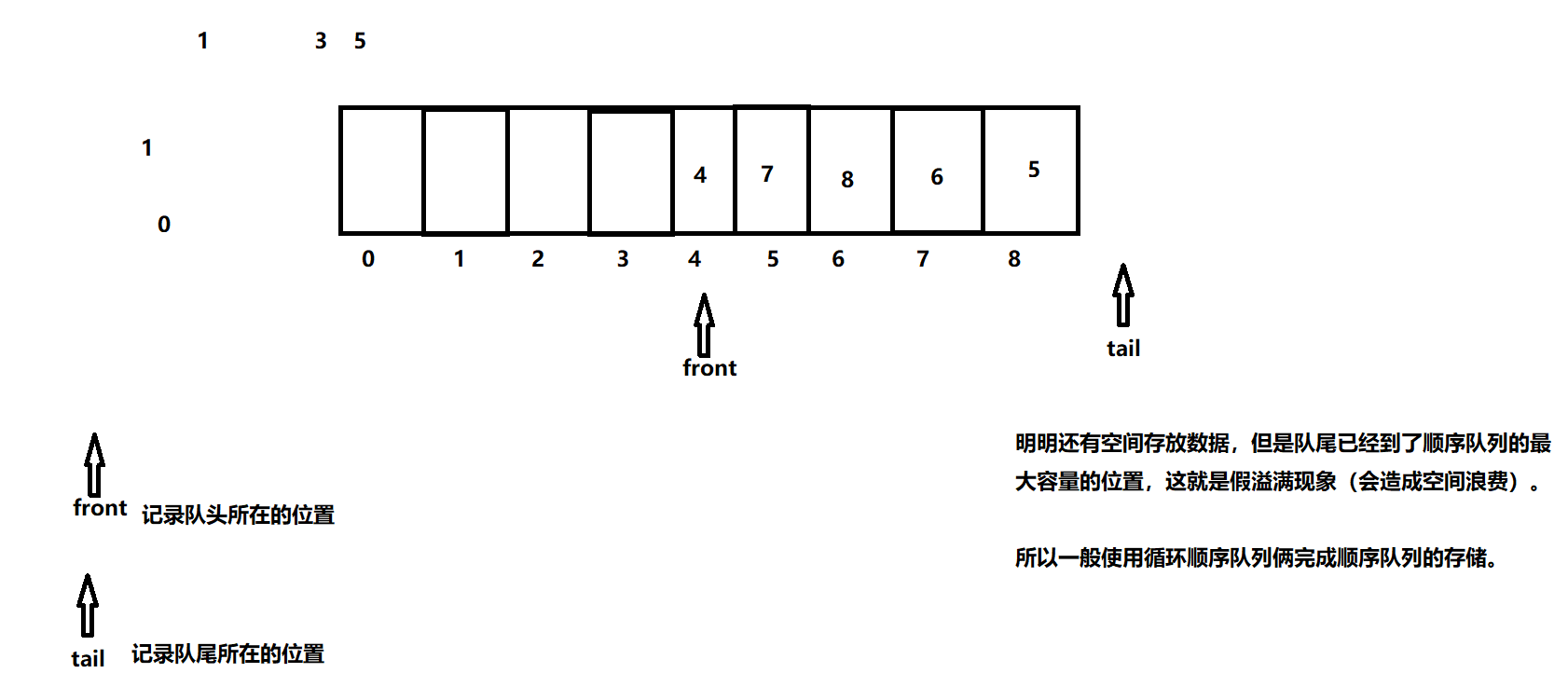
假溢满现象

还有位置存放数据，但是队尾已经到了顺序队列的最大容量的位置

所以一般采用循环队列来完成顺序队列的存储

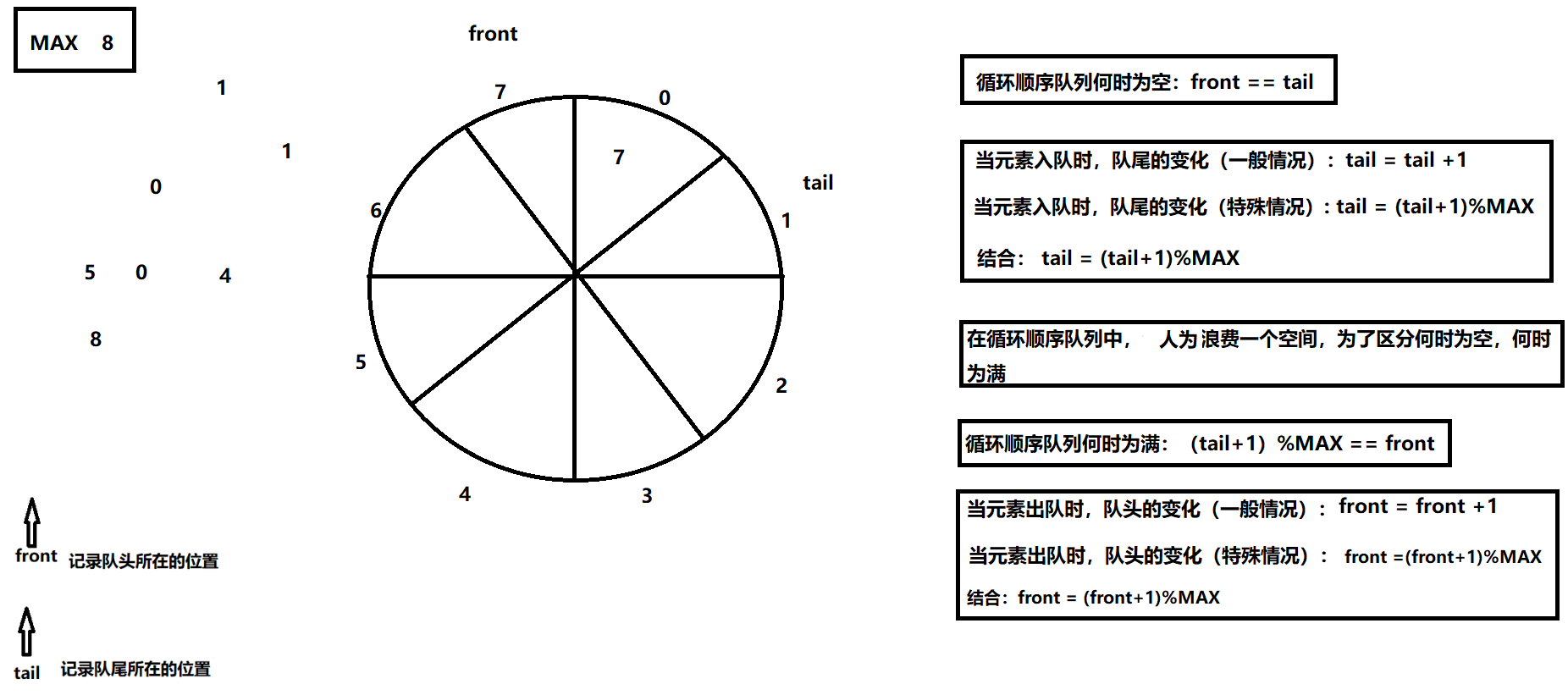
循环顺序队列

循环顺序队列的组成

需要一片连续的空间存放数据（数组，堆区的一片连续的空间）

需要一个变量记录队头的位置

需要一个变量记录队尾的位置（最后一个元素的下一个元素的位置）

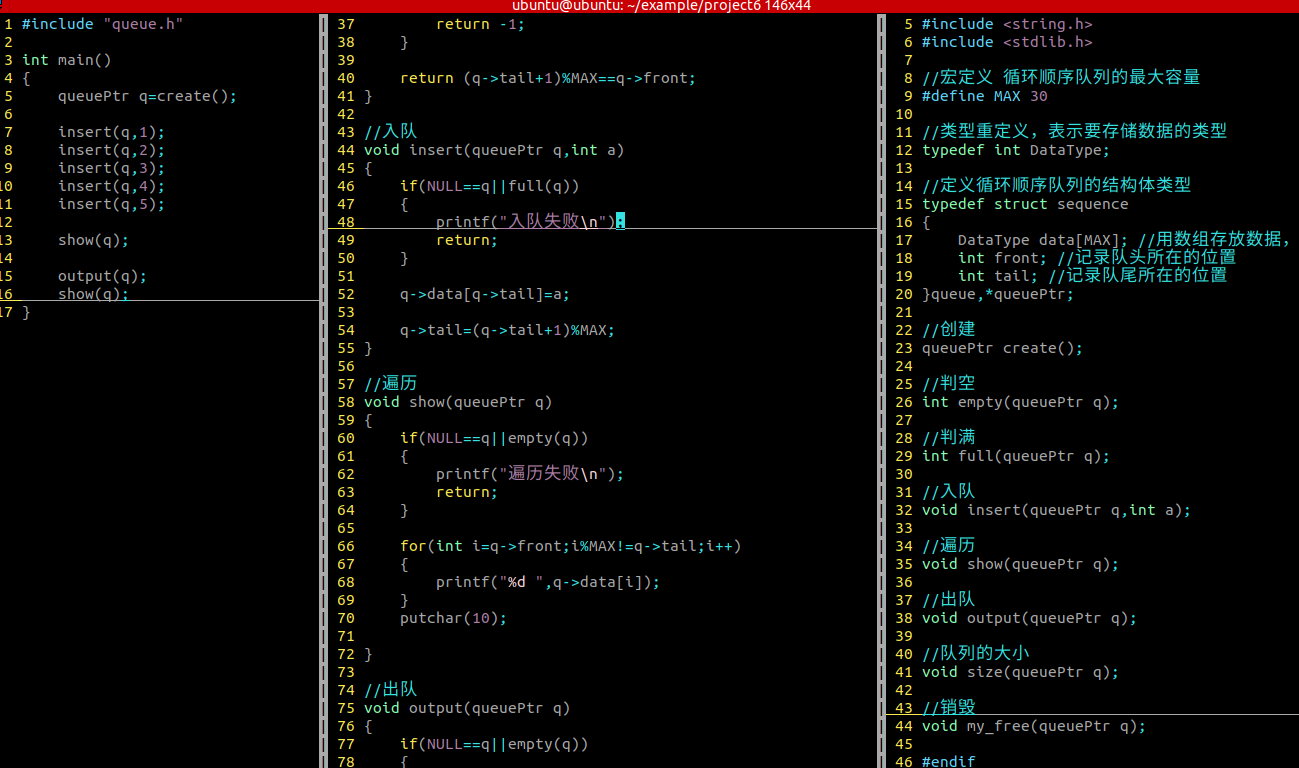
循环顺序队列的结构体原型

//宏定义 循环顺序队列的最大容量
#define MAX 30//类型重定义，表示要存储数据的类型
typedef int DataType;//定义循环顺序队列的结构体类型
typedef struct sequence
{DataType data[MAX]; //用数组存放数据，实现逻辑相连，物理内存也相连int front; //记录队头所在的位置int tail; //记录队尾所在的位置
}queue,*queuePtr;

循环顺序队列的相关操作（功能函数的封装）

创建

函数返回值：顺序栈的指针

参数列表：无

判断申请空间是否合法

判空

参数列表：顺序队列

判断申请空间是否合法

判满

参数列表：顺序队列

判断申请空间是否合法

入队

参数列表：顺序队列，入队的值

判断申请空间是否合法

需要判满

遍历

参数列表：顺序队列

判断申请空间是否合法

需要判空

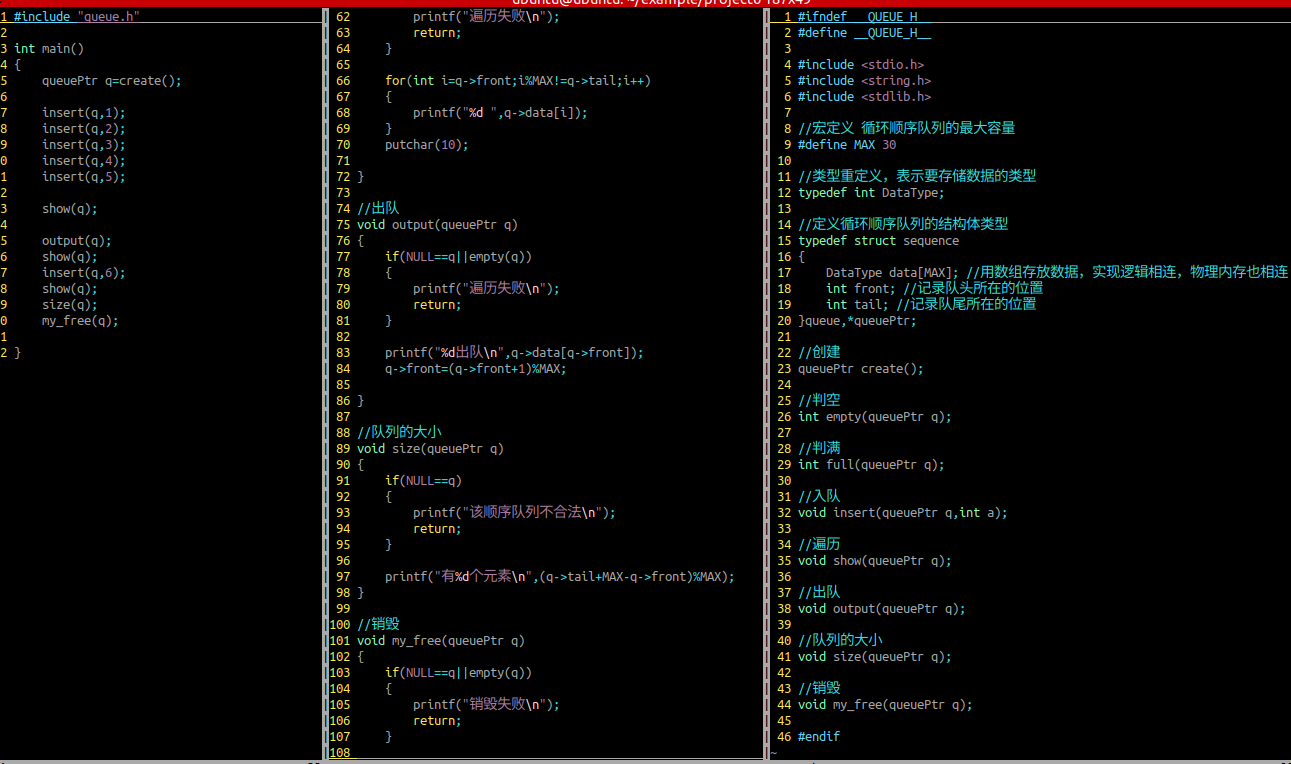
出队

参数列表：顺序队列

判断申请空间是否合法

需要判空

顺序队列的大小

参数列表：顺序队列

判断申请空间是否合法

销毁

参数列表：顺序队列

判断申请空间是否合法

链式队列

链式存储的队列（保证存储的数据逻辑上相连，物理内存上随机存储，保证满足队列的特点）

链式队列的组成

需要一片连续的空间存放数据（数组，堆区的一片连续的空间）

需要一个变量记录队头的位置

需要一个变量记录队尾的位置（最后一个元素的下一个元素的位置）

链式队列的节点的结构体原型

//重命名
typedef int DataType；
typedef struct node
{union{int len；DataType data；}；struct node *next；
}Node；typedef struct queue
{Node *front；    //记录队头Node *tail；    //记录队尾}queueLink，*queueLinkPtr；

链式队列的相关操作（功能函数的封装）

创建

参数列表：无

判断申请空间是否合法

判空

参数列表：顺序队列

判断申请空间是否合法

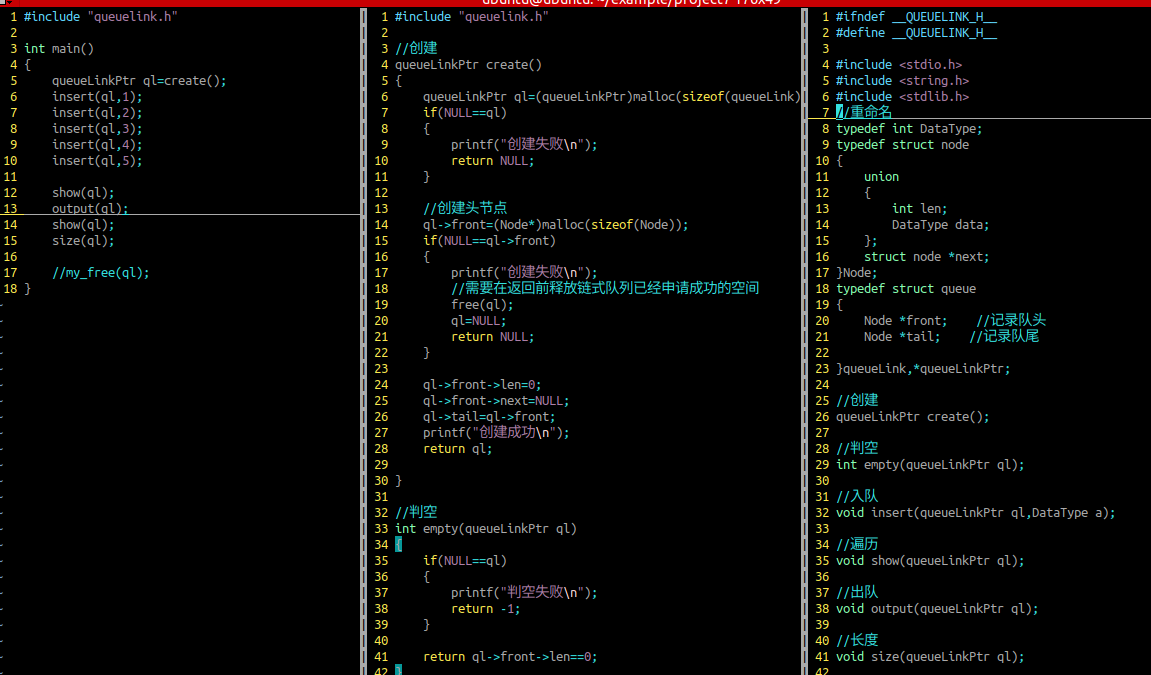
入队（尾插）

参数列表：顺序队列，入队的数据

判断申请空间是否合法

遍历

参数列表：顺序队列

判断申请空间是否合法

需要判空

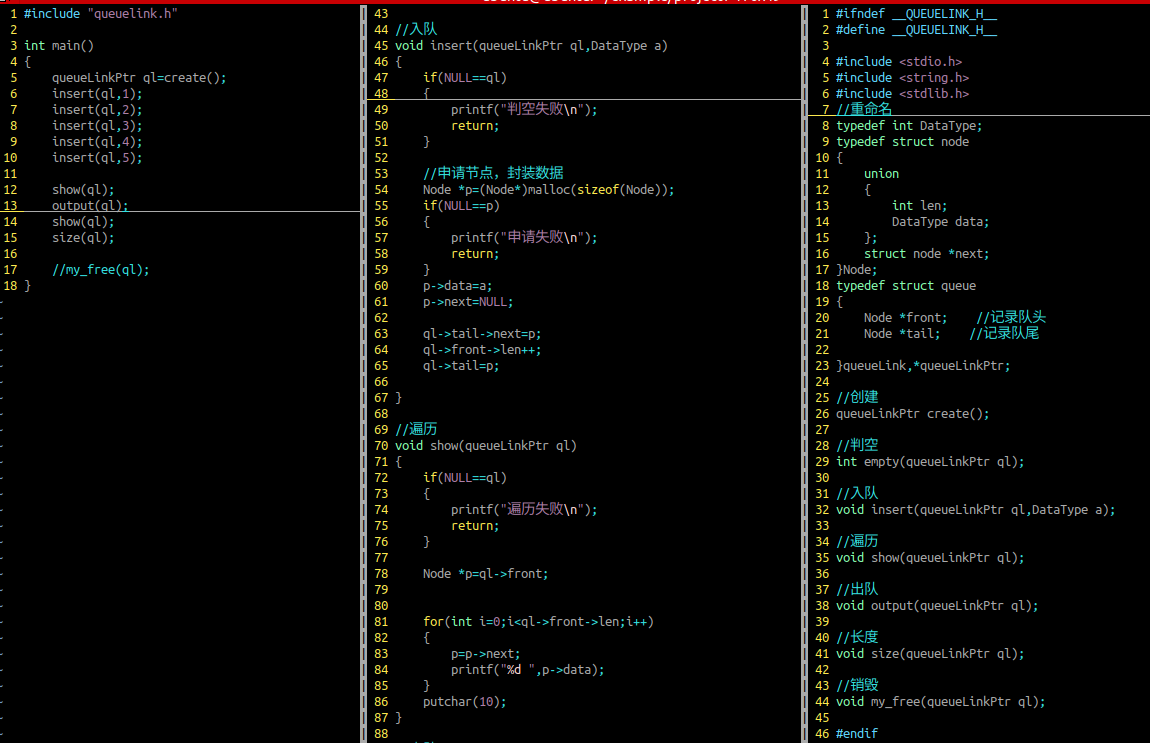
出队（头删）

参数列表：顺序队列

判断申请空间是否合法

需要判空

队列的大小

参数列表：顺序队列

判断申请空间是否合法

需要判空

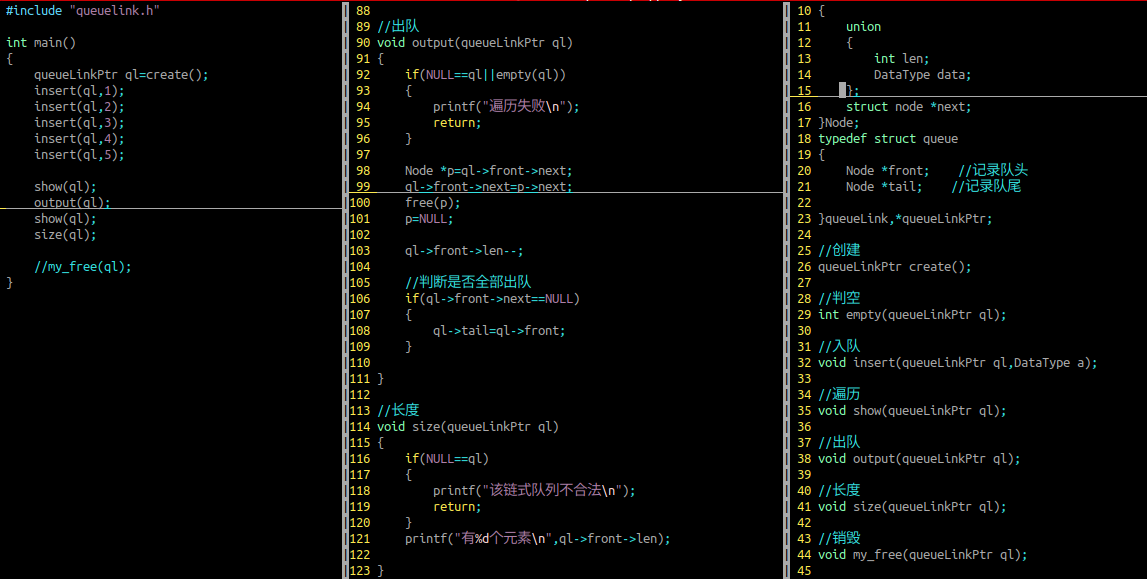
销毁

参数列表：顺序队列

判断申请空间是否合法

需要判空

 

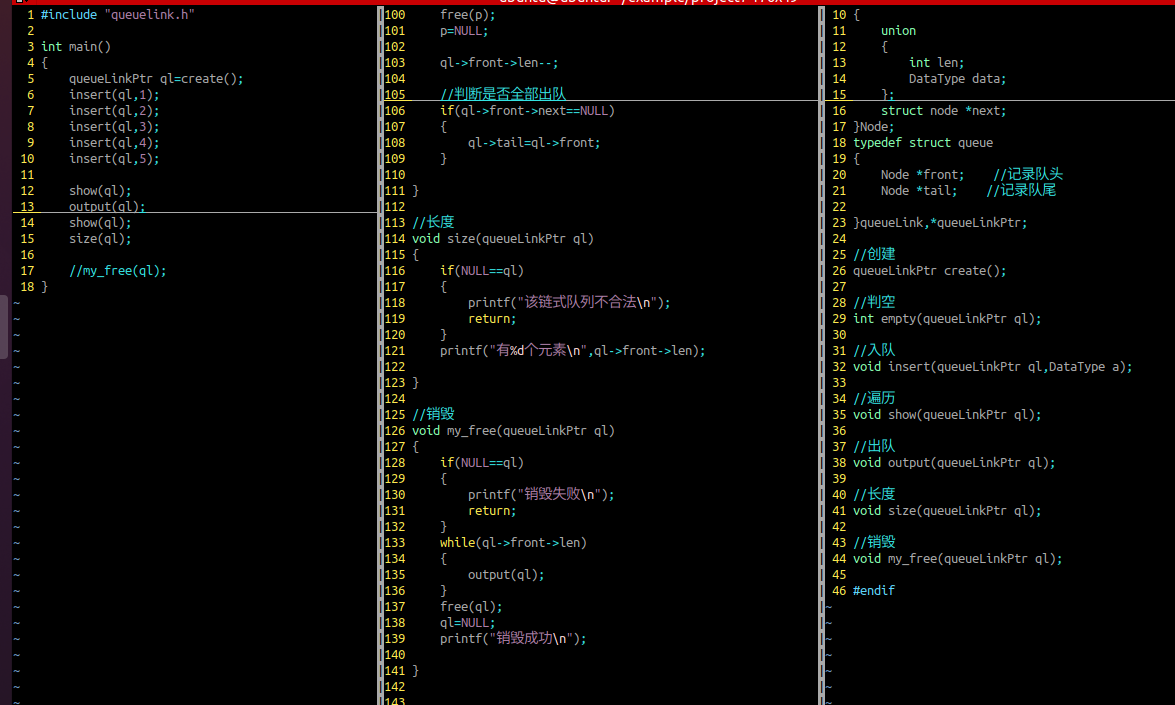
树形结构：数据元素存在一对多的关系

二叉树

每个节点最多拥有两个子节点，并且有严格的左右子树区分的树形结构

二叉树的相关概念

左子树：以当前节点的左孩子节点为根节点的子树，称为左子树。

右子树：以当前节点的右孩子节点为根节点的子树，称为右子树。

左斜树：每个节点只有左孩子节点，没有右孩子节点的树，称为左斜树。

右斜树：每个节点只有右孩子节点，没有左孩子节点的树，称为右斜树。

满二叉树：在不增加层次的基础上，不能在往树上增加节点。

完全二叉树：在满二叉树的基础上，从左往右依次增加节点的树，称为完全二叉树。

二叉树的相关概念

1、在第i层上，最多有2^(i-1)个节点
2、在第K层上，最多总共拥有 2^K-1 节点
3、在一个树上，度为0的节点（叶子节点）总比度为2的节点个数多一个。总节点个数  = 总度数 +1；
// n0 度0    n1 度1   n2 度2n0+n1+n2 = 1*n1 + 2*n2 + 1
n0 + n1 + n2 = n1 + 2n2 +1
n0 = n2 +1

二叉树的存储

满二叉树或者完全二叉树可以采用顺序存储，普通二叉树一般采用链式存储