阿里笔试2023-3-15
太菜了,记录一下笔试题目,代码有更好解法欢迎分享。
1、满二叉子树的数量。
给定一颗二叉树,试求这课二叉树有多少个节点满足以该节点为根的子树是满二叉树?满二叉树指每一层都达到节点最大值。
第一行输入n表示节点数量,接下来n行第一个代表左儿子,第二个代表右儿子。
public class Main {static int res = 0;public static void main(String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt();int[][] nums = new int[n][2];for (int i = 0; i < n; i ++) {nums[i][0] = in.nextInt();nums[i][1] = in.nextInt();}new Main().isFullTree(nums, 1);System.out.println(res);}public int height(int[][] nums, int root) {if (root == -1) {return 0;}return Math.max(height(nums, nums[root - 1][0]), height(nums, nums[root - 1][1])) + 1;}public boolean isFullTree(int[][] nums, int root) {if (root == -1) {return true;}if (isFullTree(nums, nums[root - 1][0]) && isFullTree(nums, nums[root - 1][1]) && height(nums, nums[root - 1][0]) == height(nums, nums[root - 1][1])) {res ++;return true;} else {return false;}}
}
上述解法时间复杂度O(n),空间复杂度o()
另外,可以掌握根据数组进行二叉树建树
class TreeNode {TreeNode left;TreeNode right;int val;public TreeNode() {}public TreeNode(int val) {this.val = val;}public TreeNode (TreeNode left, TreeNode right, int val) {this.left = left;this.right = right;this.val = val;}
}public static void main(String[] args) {List<TreeNode> nodeList = new ArrayList<>();nodeList.add(null);for (int i = 1; i <= n; i ++) {nodeList.add(new TreeNode(i));}for (int i = 0; i < n; i ++) {if (nums[i][0] == -1) {nodeList.get(i + 1).left = null;} else {nodeList.get(i + 1).left = nodeList.get(nums[i][0]);}if (nums[i][1] == -1) {nodeList.get(i + 1).right = null;} else {nodeList.get(i + 1).right = nodeList.get(nums[i][1]);}}
}
2、三元组计数。
给定一个数组,计算有多少个三元组0<=i<j<k<n,且max(nums[i], nums[j], nums[k]) - min(nums[i], nums[j], nums[k]) = 1。
第一行输入n表示数组个数,第二行输入n个整数。
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = scanner.nextInt();}Arrays.sort(nums);Map<Integer, Integer> map = new HashMap<>();int res = 0;for (int i = 0; i < n; i ++) {map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);}for (int i = 0; i < n; i ++) {if (i > 0 && nums[i] == nums[i - 1]) {continue;}if (map.containsKey(nums[i] + 1)) {int low = map.get(nums[i]);int high = map.get(nums[i] + 1);if (low == 1 && high == 1) {continue;}if (high > 1) {res += low * high * (high - 1) / 2;}if (low > 1) {res += high * low * (low - 1) / 2;}}}System.out.println(res);
}
上述解法时间复杂度O(nlog(n)),空间复杂度O(n)。
3、乘2除2。
在n个元素的数组中选择k个元素,每个元素要么乘以2,要么除以2并向下取整,使得操作完后数组的极差尽可能小,并且输出极差。极差为最大值减去最小值。
第一行输入整数n和k。第二行输入n个整数表示数组。
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int k = scanner.nextInt();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = scanner.nextInt();}Comparator<Integer> comparator = new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}};Arrays.sort(nums);PriorityQueue<Integer> queueMin = new PriorityQueue<>(comparator);PriorityQueue<Integer> queueMid = new PriorityQueue<>(comparator);PriorityQueue<Integer> queueMax = new PriorityQueue<>(comparator);int minMin = Integer.MAX_VALUE, midMin = Integer.MAX_VALUE, maxMin = Integer.MAX_VALUE;for (int i = 0; i < k ; i ++) {minMin = Math.min(minMin, 2 * nums[i]);queueMin.add(2 * nums[i]);}for (int i = k; i < n; i ++) {midMin = Math.min(midMin, nums[i]);queueMid.add(nums[i]);}int res = Integer.MAX_VALUE;if (k == 0) {res = Math.min(res, queueMid.peek() - midMin);} else {res = Math.min(res, Math.max(queueMin.peek(), queueMid.peek()) - Math.min(minMin, midMin));}for (int i = 0; i < k; i ++) {int tempMin = queueMin.poll();queueMid.add(tempMin / 2);midMin = Math.min(midMin, tempMin / 2);int tempMid = queueMid.poll();queueMax.add(tempMid / 2);maxMin = Math.min(maxMin, tempMid / 2);if (i == k - 1) {res = Math.min(res, Math.max(queueMid.peek(), queueMax.peek()) - Math.min(Math.min(minMin, midMin), maxMin));} else {res = Math.min(res, Math.max(Math.max(queueMin.peek(), queueMid.peek()), queueMax.peek()) - Math.min(Math.min(minMin, midMin), maxMin));}}System.out.println(res);
}
上述解法时间复杂度O(nlog(n)),空间复杂度O(n)。
相关文章:

阿里笔试2023-3-15
太菜了,记录一下笔试题目,代码有更好解法欢迎分享。 1、满二叉子树的数量。 给定一颗二叉树,试求这课二叉树有多少个节点满足以该节点为根的子树是满二叉树?满二叉树指每一层都达到节点最大值。 第一行输入n表示节点数量ÿ…...
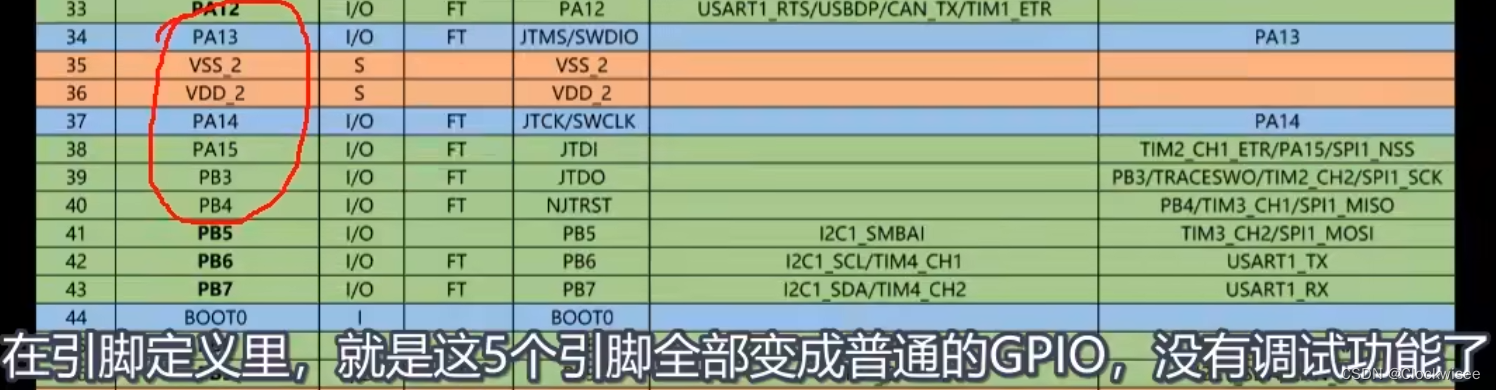
STM32:TIM定时器输出比较(OC)
一、输出比较简介 1、输出比较 OC(Output Comapre)输出比较输出比较可以通过比较CNT(时基单元)和CCR(捕获单元)寄存器值的关系,来对输出电平进行置1、置0或翻转的操作,用于输出一定频…...

HTTPS 加密协议
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录HTTPS"加密" 是什么HTTPS 的工作过程引入证书HTTPS http 安全层 (SSL) SSL 用来加密的协议,也叫 TLS …...

分布式锁和分布式事务
分布式锁 没有图形,只通过大量文字进行说明。分布式锁:redis分布式锁, zk分布式锁, 数据库做分布式锁 redis分布式锁 setnx key value ex 10 原子操作 AB两个线程减库存业务,假设库存是10 A线程获取锁,…...

RK3568平台开发系列讲解(驱动基础篇)I2C协议介绍
🚀返回专栏总目录 文章目录 一、I2C基本读写过程二、通讯的起始和停止信号三、数据有效性四、地址及数据方向五、响应沉淀、分享、成长,让自己和他人都能有所收获!😄 📢I2C的协议定义了通讯的起始和停止信号、数据有效性、响应、仲裁、时钟同步和地址广播等环节。 一、…...

HTML 音频(Audio)
HTML 音频(Audio) 声音在HTML中可以以不同的方式播放. 问题以及解决方法 在 HTML 中播放音频并不容易! 您需要谙熟大量技巧,以确保您的音频文件在所有浏览器中(Internet Explorer, Chrome, Firefox, Safari, Opera)和所有硬件上…...
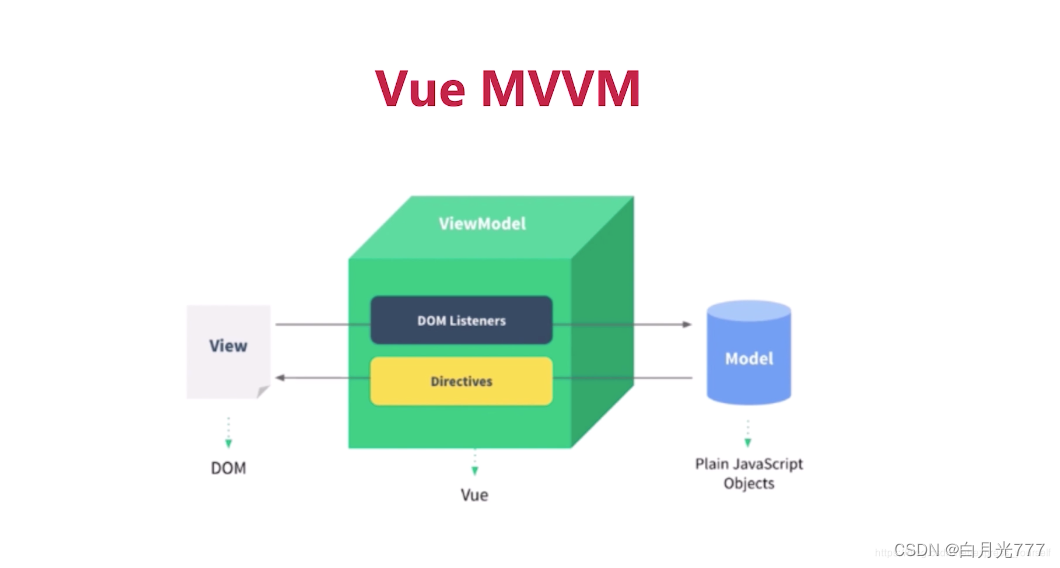
什么是Vue
✅作者简介:CSDN一位小博主,正在学习前端,欢迎大家一起来交流学习🏆 📃个人主页:白月光777的CSDN博客 🔥系列专栏:Vue从入门到进阶 💬个人格言:但行好事&…...

python 内置函数和多线程
以下是Python的一些内置函数。这些函数是Python语言提供的基本功能,可以在不需要导入任何其他模块的情况下直接使用。这些函数可以完成广泛的任务,例如数学运算,序列和集合操作,类型转换,文件操作等等。透彻理解这些函…...

【Spring】我抄袭了Spring,手写一套MySpring框架。。。
这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能 文章目录这篇博客实现了一个简单版本的Spring,主要包括Spring的Ioc和Aop功能🚀ComponentScan注解✈️Component注解🚁在spring中ioc容器的类是ApplicationConte…...
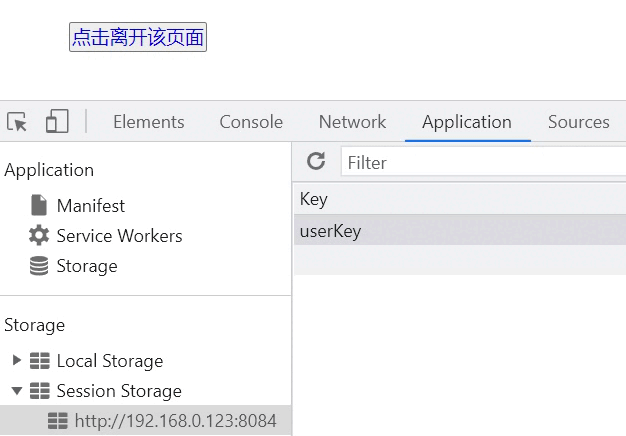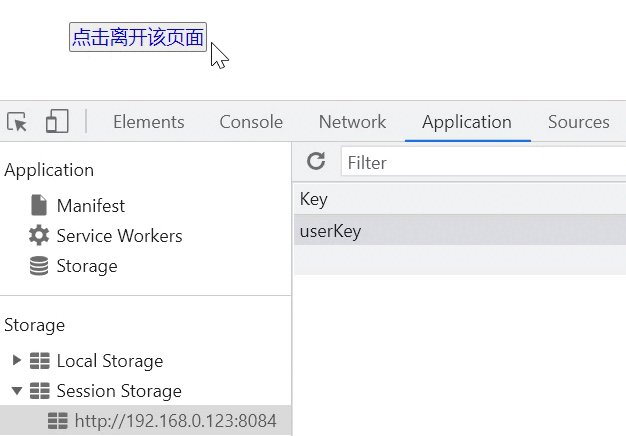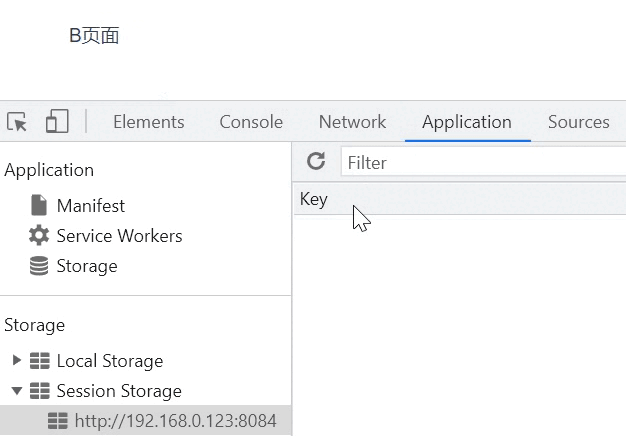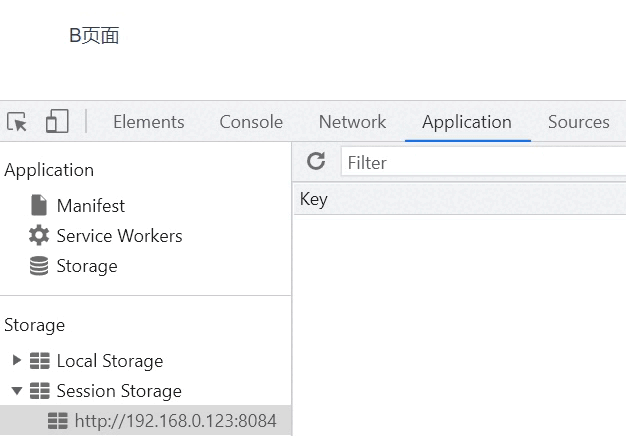
vue中的生命周期
前言 很多时候我们希望能在 vue 生命周期的过程中执行一些操作,生命周期钩子函数也因此诞生了。相信使用过 vue 框架的同学都知道,生命周期的钩子函数允许我们在实例的不同阶段执行各种操作,便于我们更好的控制和使用实例。 生命周期钩子函数…...
)
硬件原理图设计规范(二)
1、可编程逻辑器件 编号 级别 条目内容 备注 1 推荐 FPGA的LE资源利用率要保证在50%~80%之间,EPLD的MC资源的利用率要保证在50%~90%之间。对于FPGA中的锁相环、RAM、乘法器、DSP单元、CPU核等资源,经过精确预算,…...

复旦微ZYNQ7020全国产替代方案设计
现在国产化进度赶人,进口的芯片只做了个功能验证,马上就要换上国产的。国内现在已经做出来zynq的只有复旦微一家,已经在研制的有上海安路,还有成都华微(不排除深圳国威也在做,毕竟这个市场潜力很大…...
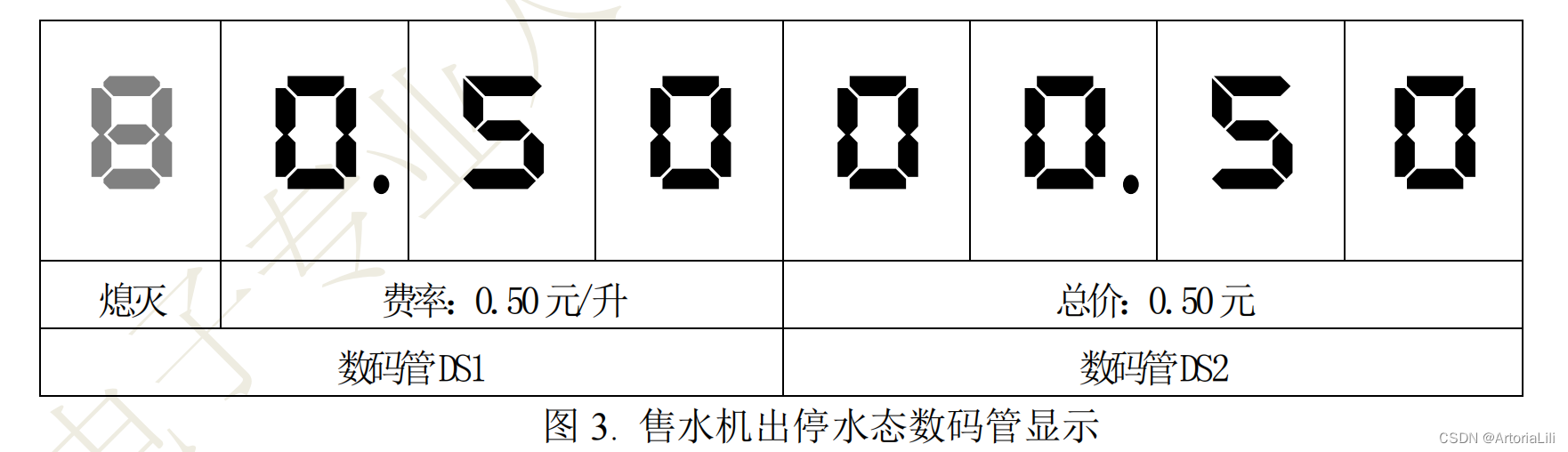
蓝桥杯真题——自动售水机
2012年第四届全国电子专业人才设计与技能大赛“自动售水机”设计任务书1. 系统框图接下来我们将任务分块: 1. 按键控制单元 设定按键 S7 为出水控制按键,当 S7 按下后,售水机持续出水(继电器接通,指示 灯 L10 点亮&…...

软件质量保证与测试 课程设计 测试报告 缺陷报告撰写方法
测 试 报 告 2020年 6月 1日 测试项目 程序员 测试人 测试阶段: □集成 √系统 □ 测试日志编号清单 1,2,3,4,5,6,7,8,9,10 遗留错误说明:(测试后仍然遗留下来未解决的错误及其说明) 1.系统界面不够友好&…...

vue2和vue3中路由的区别和写法?
前言:Vue 2 和 Vue 3 中路由的主要区别在于使用的路由库不同。在 Vue 2 中,通常使用 Vue Router 作为路由库;而在 Vue 3 中,Vue Router 仍然是官方推荐的路由库,但也可以选择使用新的路由库 - Vue Router Next。下面分…...
)
【数据结构】第四站:单链表力扣题(一)
目录 一、移除链表元素 二、链表的中间结点 三、链表中倒数第k个结点 四、反转链表 五、合并两个有序链表 六、分割链表 一、移除链表元素 题目描述:力扣 法一:直接循环依次判断 对于这个题目,我们最容易想到的一种思路就是,…...

SAP BPC简介
BPC是SAP在financial application领域主推的产品,由于从原有产品线发展而来,产品本身有两个版本,分别是基于MS OLAP平台和Netweaver OLAP平台。 整个系统分为.net前台和abap后台。由于abap端的数据结构与.net数据结构的差异,所以没…...
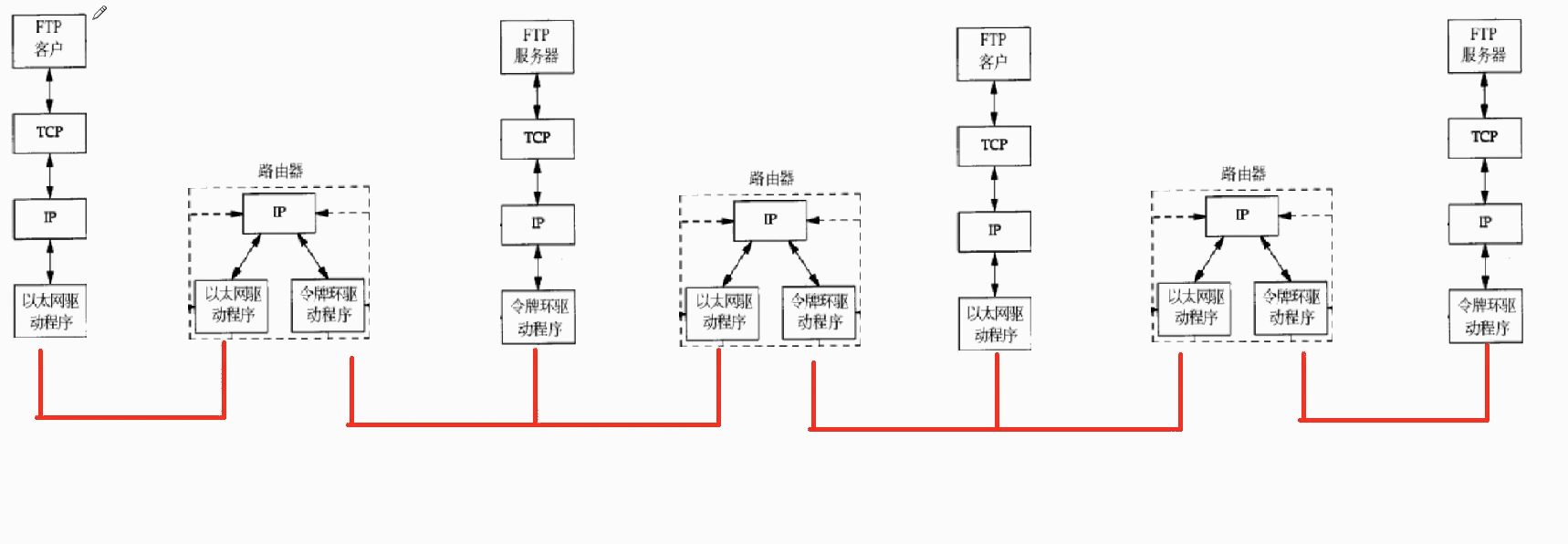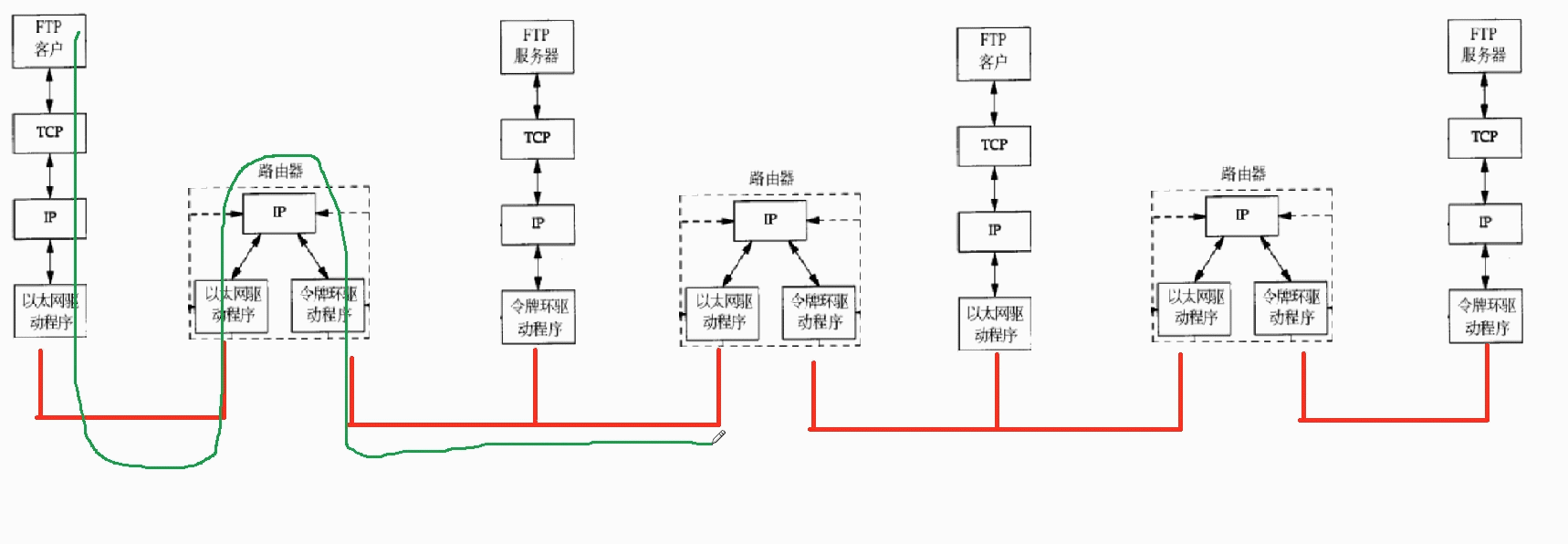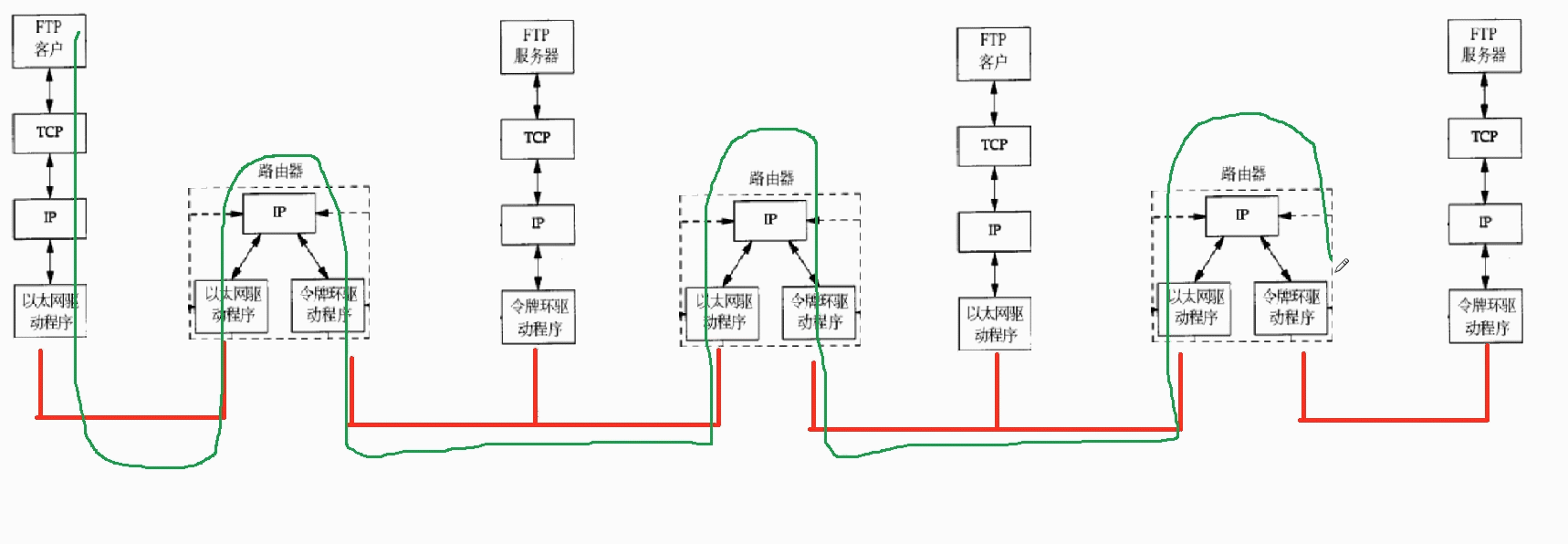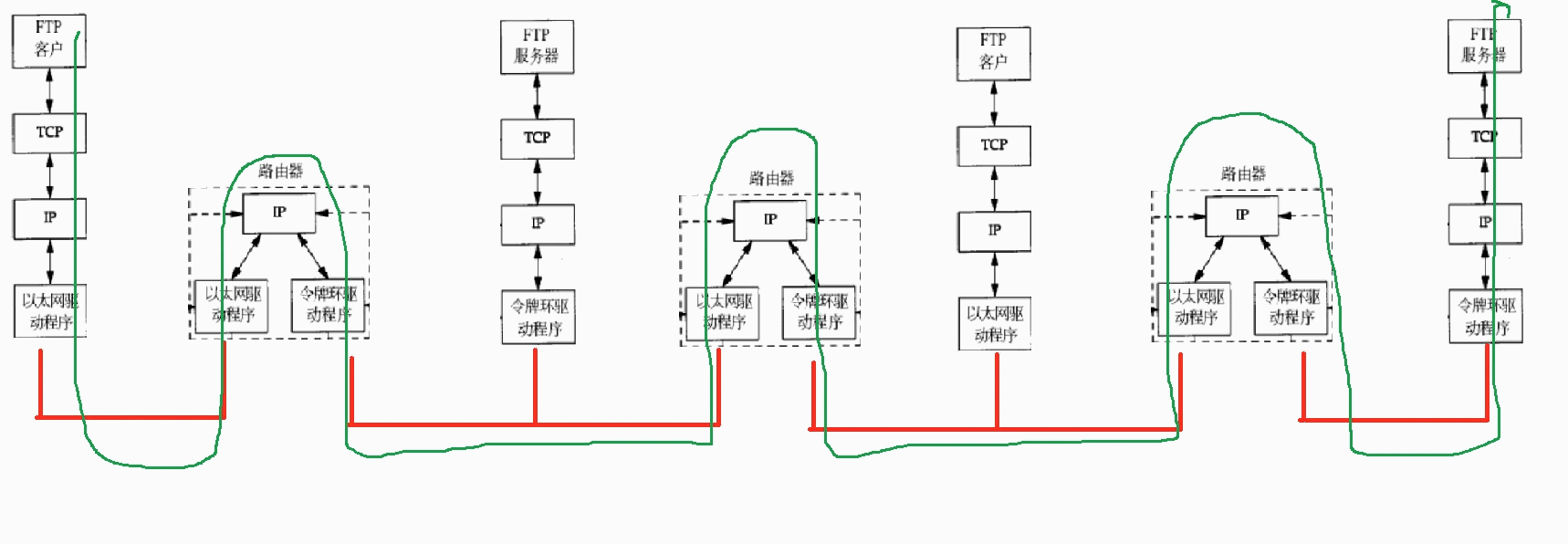
Linux网络概述
写咋前面 今天,我们需要初步的认识一下Linux中网络的基本原理,只有大家对这个有一个初步的认识,后面我们学习起来才会更加的简单容易.计算机语言知识那么多,但是Linux不是.面试时,面试官总是会有问题难住你,我们后面需要看看书,这一点非常重要.我们现在谈的是脉络,.是框架.这些…...

Mybatis --- 获取参数值和查询功能
一、MyBatis的增删改查 1.1、新增 <!--int insertUser();--> <insert id"insertUser">insert into t_user values(null,admin,123456,23,男) </insert> 1.2、删除 <!--int deleteUser();--> <delete id"deleteUser">dele…...

【C++】C++入门,你必须要知道的知识
1.C关键字 🔥前言: C是在C的基础之上,容纳进去了面向对象编程思想,并增加了许多有用的库,以及编程范式等。熟悉C语言之后,对C学习有一定的帮助。今天的主要目标: 1️⃣ 补充C语言语法的不足&…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
