Educational Codeforces Round 168 (Rated for Div. 2)-7.30复盘
A. Strong Password
简单题,找到相同的两个相邻字母之间插一个跟他们不同的大写字母即可
inline void solve(){cin>>s;int id=0;char hh=' ';for(int i=1;i<s.size();i++){if(s[i-1]==s[i]){id=i;break;}} for(int i=0;i<26;i++){if(s[id]!='a'+i&&s[id+1]!='a'+i) hh='a'+i;}for(int i=0;i<s.size();i++){if(id==i) cout<<hh;cout<<s[i];}cout<<endl;
}B. Make Three Regions
观察给的样例,只有两个箱子夹着,并且上一行或下一行往右或者往左没有箱子,那这个位置就是答案所在的位置,统计这种类型位置的数目即可

inline void solve(){cin>>n;int sum=0;for(int i=0;i<2;i++){for(int j=0;j<n;j++) cin>>g[i][j];}for(int i=0;i<2;i++){for(int j=0;j<n;j++){if(j+2>=n) continue;if(g[i][j]=='x'&&g[i][j+1]=='.'&&g[i][j+2]=='x'){if(i==0&&g[i+1][j+2]=='.'&&g[i+1][j]=='.') sum++;else if(i==1&&g[i-1][j+2]=='.'&&g[i-1][j]=='.') sum++;}}}cout<<sum<<endl;
}C. Even Positions
刚开始看以为是那种很恶心的括号的dp,没想到画了几个样例,发现贪心能做,每次枚举偶数位置,看是什么类型的括号,左括号就往右边找,右括号就往左边找,找最近且没被使用过的的位置即可
inline void solve(){cin>>n;int sum=0;for(int i=1;i<=n;i++) cin>>g[i];for(int i=1;i<=n;i++){i++;if(g[i]=='('){for(int j=1;j<=n-i;j++){if(j!=1) j++;if(!st[i+j]){st[i+j]=1;sum+=j;break;}}}else{for(int j=1;j<=i;j++){if(j!=1) j++;if(!st[i-j]){st[i-j]=1;sum+=j;break;}}}}cout<<sum<<endl;for(int i=1;i<=n;i++) st[i]=0;
}D. Maximize the Root
用dfs搜索找出每个分支的最小值,最小值如果大于该分支定点的值,就更新该顶点的值为该顶点的值加上最小值的和除以2,否则用最小值更新该分支定点的值
ll dfs(ll x){if(!e[x].size()){if(x==1) ans=a[x];return a[x];}ll mn=1e9+1;for(auto u:e[x]){mn=min(mn,dfs(u));}if(x==1) ans=a[x]+mn;if(a[x]>=mn) return mn;return (a[x]+mn)/2;
}void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=2;i<=n;i++){cin>>h;e[h].push_back(i);}ans=0;dfs(1);cout<<ans<<endl;for(int i=1;i<=n;i++) e[i].clear();
}相关文章:

Educational Codeforces Round 168 (Rated for Div. 2)-7.30复盘
A. Strong Password 简单题,找到相同的两个相邻字母之间插一个跟他们不同的大写字母即可 inline void solve(){cin>>s;int id0;char hh ;for(int i1;i<s.size();i){if(s[i-1]s[i]){idi;break;}} for(int i0;i<26;i){if(s[id]!ai&&s[id1]!ai) …...

Web开发:小结Apache Echarts官网上常用的配置项(前端可视化图表)
目录 一、须知 二、Title 三、 Legend 四、Grid 一、须知 配置项官方文档:点此进入。 我总结了比较常用的功能,写进注释里面,附带链接分享和效果图展示。(更新中....) 二、Title option {title: {text: Weekl…...

B树的平衡性与性能优化
B树的平衡性与性能优化 B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于保持数据的有序性并允许高效的插入、删除和查找操作。B树能够很好地处理大规模数据,并在磁盘I/O操作中表现出色。本文…...

llama3源码解读之推理-infer
文章目录 前言一、整体源码解读1、完整main源码2、tokenizer加载3、llama3模型加载4、llama3测试数据文本加载5、llama3模型推理模块1、模型推理模块的数据处理2、模型推理模块的model.generate预测3、模型推理模块的预测结果处理6、多轮对话二、llama3推理数据处理1、完整数据…...

【教程】Linux安装Redis步骤记录
下载地址 Index of /releases/ Downloads - Redis 安装redis-7.4.0.tar.gz 1.下载安装包 wget https://download.redis.io/releases/redis-7.4.0.tar.gz 2.解压 tar -zxvf redis-7.4.0.tar.gz 3.进入目录 cd redis-7.4.0/ 4.编译 make 5.安装 make install PREFIX/u…...

全球汽车线控制动系统市场规模预测:未来六年CAGR为17.3%
引言: 随着汽车行业的持续发展和对安全性能需求的增加,汽车线控制动系统作为提升车辆安全性和操控性的关键组件,正逐渐受到市场的广泛关注。本文旨在通过深度分析汽车线控制动系统行业的各个维度,揭示行业发展趋势和潜在机会。 【…...

Ubuntu运行深度学习代码,代码随机epoch中断没有任何报错
深度学习运行代码直接中断 文章目录 深度学习运行代码直接中断问题描述设备信息问题补充解决思路问题发现及正确解决思路新问题出现最终问题:ubuntu系统,4090显卡安装英伟达驱动535.x外的驱动会导致开机无法进入桌面问题记录 问题描述 运行深度学习代码…...

只有4%知道的Linux,看了你也能上手Ubuntu桌面系统,Ubuntu简易设置,源更新,root密码,远程服务...
创作不易 只因热爱!! 热衷分享,一起成长! “你的鼓励就是我努力付出的动力” 最近常提的一句话,那就是“但行好事,莫问前程"! 与辉同行的董工说:守正出奇。坚持分享,坚持付出,坚持奉献,…...
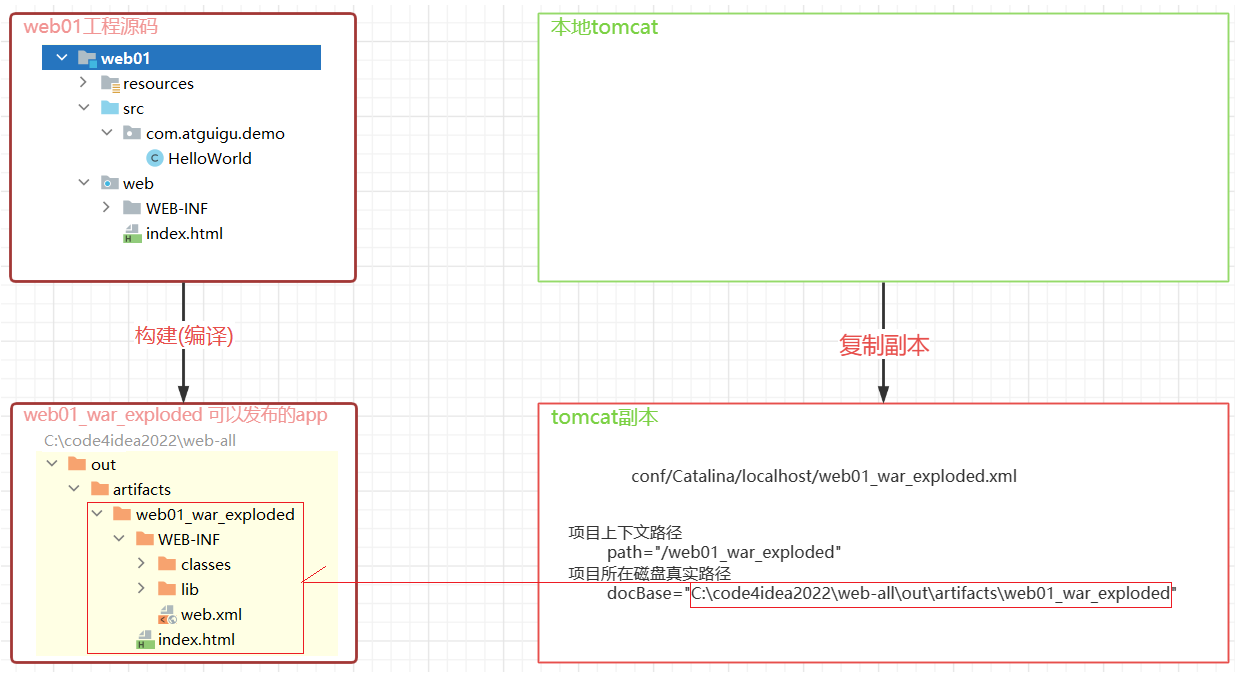
Tomcat部署——个人笔记
Tomcat部署——个人笔记 文章目录 [toc]简介安装配置文件WEB项目的标准结构WEB项目部署IDEA中开发并部署运行WEB项目 本学习笔记参考尚硅谷等教程。 简介 Apache Tomcat 官网 Tomcat是Apache 软件基金会(Apache Software Foundation)的Jakarta 项目中…...

常见且重要的用户体验原则
以下是一些常见且重要的用户体验原则: 1. 以用户为中心 - 深入了解用户的需求、期望、目标和行为习惯。通过用户研究、调查、访谈等方法获取真实的用户反馈,以此来设计产品或服务。 - 例如,在设计一款老年手机时,充分考虑老年…...

web基础及nginx搭建
第四周 上午 静态资源 根据开发者保存在项目资源目录中的路径访问静态资源 html 图片 js css 音乐 视频 f12 ,开发者工具,网络 1 、 web 基本概念 web 服务器( web server ):也称 HTTP 服务器( HTTP …...

C++ 布隆过滤器
1. 布隆过滤器提出 我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉 那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用 户看过的所有历史…...

使用HTML创建用户注册表单
在当今数字化时代,网页表单对于收集用户信息和促进网站交互至关重要。无论您设计简单的注册表单还是复杂的调查表,了解HTML的基础知识可以帮助您构建有效的用户界面。在本教程中,我们将详细介绍如何使用HTML创建基本的用户注册表单。 第一步…...

Python零基础入门教程
Python零基础详细入门教程可以从以下几个方面进行学习和掌握: 一、Python基础认知 1. Python简介 由来与发展:Python是一种广泛使用的高级编程语言,由Guido van Rossum(吉多范罗苏姆)于1991年首次发布。Python以其简…...

成为git砖家(10): 根据文件内容生成SHA-1
文章目录 1. .git/objects 目录2. git cat-file 命令3. 根据文件内容生成 sha-14. 结语5. References 1. .git/objects 目录 git 是一个根据文件内容进行检索的系统。 当创建 hello.py, 填入 print("hello, world")的内容, 并执行 git add hello.py gi…...

园区导航小程序:一站式解决园区导航问题,释放存储,优化访客体验
随着园区的规模不断扩大,功能区划分日益复杂,导致访客和新员工在没有有效导航的情况下容易迷路。传统APP导航虽能解决部分问题,但其下载安装繁琐、占用手机内存大、且非高频使用导致的闲置,让许多用户望而却步。园区导航小程序的出…...
)
对于n进制转十进制的解法及代码(干货!)
对于p进制转十进制,我们有:(x)pa[0]*p^0a[1]*p^1a[2]*p^2...a[n]*p^n 举个例子:(11001)21*10*20*41*81*1625 (9FA)1610*16^015*16^19*16^22554 据此,我们可以编出c代码来解决问题 …...

当代互联网打工人的生存现状,看完泪流满面!
欢迎私信小编,了解更多产品信息呦~...

花几千上万学习Java,真没必要!(三十八)
测试代码1: package iotest.com; import java.nio.charset.StandardCharsets; import java.io.UnsupportedEncodingException; public class StringByteConversion { public static void main(String[] args) throws UnsupportedEncodingException { // 原始字…...

Zilliz 2025届校园招聘正式启动,寻找向量数据库内核开发工程师
为了解决非结构化数据处理问题,我们构建了向量数据库-Milvus! Milvus 数据库不仅是顶级开源基金会 LF AI&Data 的毕业项目,还曾登上数据库顶会SIGMOD、VLDB,在全球首届向量检索比赛中夺冠。目前,Milvus 项目已获得超过 2.8w s…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
