排序算法:快速排序,golang实现
目录
前言
快速排序
代码示例
1. 算法包
2. 快速排序代码
3. 模拟程序
4. 运行程序
5. 从大到小排序
快速排序的思想
快速排序的实现逻辑
1. 选择基准值 (Pivot)
2. 分区操作 (Partition)
3. 递归排序
循环次数测试
假如 10 条数据进行排序
假如 20 条数据进行排序
假如 30 条数据进行排序
假设 5000 条数据,对比 冒泡、选择、插入、堆、归并
快速排序的适用场景
1. 大数据集
2. 随机数据
3. 缓存友好的
前言
在实际场景中,选择合适的排序算法对于提高程序的效率和性能至关重要,本节课主要讲解"快速排序"的适用场景及代码实现。
快速排序
快速排序(Quick Sort) 是一种非常高效的排序算法,采用分治法的策略来把一个序列分为较小和较大的两个子序列,然后递归地排序两个子序列。其基本思想是:选择一个基准值(pivot),通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以达到整个数据变成有序序列。
代码示例
下面我们使用Go语言实现一个快速排序
1. 算法包
创建一个 pkg/algorithm.go
touch pkg/algorithm.go(如果看过上节课的插入排序,则已存在该文件,我们就不需要再创建了)
2. 快速排序代码
打开 pkg/algorithm.go 文件,代码如下
从小到大 排序
package pkg// BubbleSort 冒泡排序
...// SelectionSort 选择排序
...// InsertionSort 插入排序
...// QuickSort 快速排序
func QuickSort(arr []int, low, high int) {if low < high {// partitionIndex 是分区操作后基准的索引partitionIndex := partition(arr, low, high)// 分别对基准左侧和右侧的子数组进行快速排序QuickSort(arr, low, partitionIndex-1)QuickSort(arr, partitionIndex+1, high)}
}// partition 分区操作
func partition(arr []int, low, high int) int {pivot := arr[high] // 选择最后一个元素作为基数i := low - 1for j := low; j < high; j++ {// 如果当前元素小于或等于基数if arr[j] <= pivot {i++// 交换 arr[i] 和 arr[j]arr[i], arr[j] = arr[j], arr[i]}}// 交换 arr[i+1] 和 arr[high] (基准值)arr[i+1], arr[high] = arr[high], arr[i+1]return i + 1
}
3. 模拟程序
打开 main.go 文件,代码如下:
package mainimport ("demo/pkg""fmt"
)func main() {// 定义一个切片,这里我们模拟 10 个元素arr := []int{51, 224, 67, 322, 825, 103, 50, 965, 789, 601}fmt.Println("Original data:", arr) // 先打印原始数据pkg.QuickSort(arr, 0, len(arr)-1) // 调用快速排序fmt.Println("New data: ", arr) // 后打印排序后的数据
}
4. 运行程序
go run main.go
能发现, Original data 后打印的数据,正是我们代码中定义的切片数据,顺序也是一致的。
New Data 后打印的数据,则是经过快速排序后的数据,是从小到大的。
5. 从大到小排序
如果需要 从大到小 排序也是可以的,在代码里,将两个元素比较的 小于等于符号 改成 大于等于符号 即可。
修改 pkg/algorithm.go 文件:
package pkg// BubbleSort 冒泡排序
...// SelectionSort 选择排序
...// InsertionSort 插入排序
...// QuickSort 快速排序
func QuickSort(arr []int, low, high int) {if low < high {// partitionIndex 是分区操作后基准的索引partitionIndex := partition(arr, low, high)// 分别对基准左侧和右侧的子数组进行快速排序QuickSort(arr, low, partitionIndex-1)QuickSort(arr, partitionIndex+1, high)}
}// partition 分区操作
func partition(arr []int, low, high int) int {pivot := arr[high] // 选择最后一个元素作为基数i := low - 1for j := low; j < high; j++ {// 如果当前元素大于或等于基数if arr[j] >= pivot {i++// 交换 arr[i] 和 arr[j]arr[i], arr[j] = arr[j], arr[i]}}// 交换 arr[i+1] 和 arr[high] (基准值)arr[i+1], arr[high] = arr[high], arr[i+1]return i + 1
}
只需要一丁点的代码即可
从 package pkg 算第一行,上面示例中在第三十一行代码中,我们将 "<=" 改成了 ">=" ,这样就变成了 从大到小排序了
快速排序的思想
- 分而治之:将大问题分解为小问题,然后递归地解决小问题,最后将小问题的解合并成原问题的解
- 原地排序:快速排序是原地排序算法,它只需要一个很小的栈空间(用于递归)来进行排序,不需要额外的存储空间
- 不稳定性:快速排序在某些情况下可能不是稳定的排序算法,因为相同元素的相对位置可能会在排序过程中改变
快速排序的实现逻辑
1. 选择基准值 (Pivot)
- 在快速排序中,首先需要选择一个基准值(pivot)。基准值的选择对排序的效率有很大的影响,但在本文的示例代码中,我们简单地选择了数组的最后一个元素作为基准值
2. 分区操作 (Partition)
- 分区操作是快速排序的核心。它的目的是将数组重新排列,使得所有比基准值小的元素都移到基准值的左边,所有比基准值大的元素都移到右边。分区操作完成后,基准值就处于其最终排序位置
- 在 partition 函数中,我们使用两个指针 i 和 j,其中 i 指向小于基准值的最后一个元素的下一个位置(初始化为 low - 1), j 用于遍历数组 (从 low 开始到 high - 1)。当 arr[j] 小于或等于基准值时,我们将其与 arr[i+1] 交换,并将 i 增加 1。这样,所有小于或等于基准值的元素都被交换到了基准值的左边
- 最后,我们将基准值 (原本在 arr[high] ) 与 arr[i + 1] 交换,此时 i + 1 就是基准值的最终位置,也是分区操作的返回值
3. 递归排序
- 分区操作完成后,我们得到了基准值的正确位置,并且数组被分成了两部分:一部分是基准值左边的所有元素 (都比基准值小),另一部分是基准值右边的所有元素 (都比基准值大)
- 然后,我们递归地对这两部分分别进行快速排序。这是通过调用 QuickSort 函数,并传入适当的参数 (基准值左侧和右侧的子数组的范围) 来实现的
循环次数测试
按照上面示例进行测试
假如 10 条数据进行排序
[]int{51, 224, 67, 322, 825, 103, 50, 965, 789, 601}总计循环了 30 次
假如 20 条数据进行排序
[]int{997, 387, 461, 530, 979, 502, 36, 459, 99, 60, 454, 37, 182, 273, 529, 130, 315, 351, 975, 497}总计循环了 83 次
假如 30 条数据进行排序
[]int{755, 247, 642, 652, 38, 587, 387, 284, 476, 924, 339, 830, 614, 534, 832, 450, 8, 641, 768, 788, 472, 750, 169, 479, 386, 124, 868, 259, 550, 613}总计循环了 138 次
上面我们说到,"基准值的选择对排序的效率有很大的影响",我们修改一条,依旧使用 30 条数据,我们将其最后一位数据 613,改成其他数 120 (这个值可随便改,这里示例 120)
通过调试,循环了 151 次
如果将 120 改成 700
通过调试,循环了 131 次
假设 5000 条数据,对比 冒泡、选择、插入、堆、归并
- 冒泡排序:循环次数 12,502,499 次
- 选择排序:循环次数 12,502,499 次
- 插入排序:循环次数 6,323,958 次
- 快速排序:循环次数 74,236 次
- 堆排序:循环次数 59,589 次
- 归并排序:循环次数 60,288 次
快速排序的适用场景
快速排序在多种情况下都是非常高效的,特别是以下几种情况:
1. 大数据集
对于大数据集,快速排序通常比简单的排序算法 (如 冒泡排序、插入排序) 更快
2. 随机数据
当输入数组中的数据是随机分布的时,快速排序的平均时间复杂度是 O(n log n),这是非常高效的
3. 缓存友好的
快速排序通过递归地在数组的不同部分上工作,倾向于产生良好的缓存局部性,特别是在处理大数据集时
然后,快速排序在某些情况下可能不是最佳选择,例如:
- 小数据集:对于非常小的数据集,快速排序的递归开销可能使得它不如简单的排序算法 (如 插入排序) 快
- 几乎已经排序的数据:在这种情况下,快速排序的性能可能退化为 O(n^2),因为它依赖于分区操作来减少问题的规模。如果分区操作不能有效地减少数组的大小 (例如,基准值总是最大或最小的元素),则会导致性能下降。在这种情况下,可以考虑使用归并排序或堆排序等算法
- 不稳定的排序需求:虽然快速排序在大多数情况下是稳定的 (如果实现得当),但在某些特定实现中可能不是。如果稳定性是排序算法的一个关键要求,可能需要考虑其他算法
相关文章:

排序算法:快速排序,golang实现
目录 前言 快速排序 代码示例 1. 算法包 2. 快速排序代码 3. 模拟程序 4. 运行程序 5. 从大到小排序 快速排序的思想 快速排序的实现逻辑 1. 选择基准值 (Pivot) 2. 分区操作 (Partition) 3. 递归排序 循环次数测试 假如 10 条数据进行排序 假如 20 条数据进行…...

step:菜单栏静态加载和动态加载
文章目录 文章介绍静态加载动态加载补充材料 文章介绍 对比静态加载和动态加载。 主界面main.qml之前使用的是动态加载,动态加载导致的问题:菜单栏选择界面切换时,之前的界面内容被清空。 修改方法:将动态加载改为静态加载 左边是…...

【简历】武汉某985大学:前端简历指导,拿offer可能性低
注:为保证用户信息安全,姓名和学校等信息已经进行同层次变更,内容部分细节也进行了部分隐藏 简历说明 这是一份985武汉某大学25届的前端简历,那么985面向的肯定是大厂的层次,但是作为前端简历,学校部分&a…...

推荐系统的核心逻辑 MVP
我们将设计一个基于内容经济的推荐系统(Minimum Viable Product, MVP)。这个系统将通过收集用户行为数据,计算用户相似度,并生成个性化的推荐结果。推荐系统将包括数据收集、数据存储、数据处理和推荐服务几个关键部分。 MVP功能…...

Java中的BIO,NIO与操作系统IO模型的区分
Java中的IO模型 Java中的BIO,NIO,AIO概念可以是针对输入输出流,文件,和网络编程等其他IO操作的。 但是主要还是在网络编程通信过程中比较重要,因为很多情况网络编程需要它们来提供更好的性能。 所以本篇文章偏向于网络…...

AI砸掉了这些人的饭碗
在一般打工人眼里,金融圈往往被认为是高端脑力工作者的聚集地,他们工资高,学历高,能力强,轻易无法被替代。 可最近,偏偏一个“非人类”的物种,要来抢他们的饭碗。相关报道称,华尔街…...

端口及对应服务
端口是计算机网络中用于区分不同服务的逻辑概念。每个端口号都是一个16位的数字,其取值范围从0到65535。端口号被分为以下几类: 公认端口(Well-known ports):范围从0到1023,这些端口通常被分配给常见的服务…...

剑指offer题解合集——Week7day1[滑动窗口的最大值]
滑动窗口的最大值 题目描述 给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。 例如,如果输入数组 [2,3,4,2,6,2,5,1] 及滑动窗口的大小 3 ,那么一共存在 6 个滑动窗口,它们的最大值分别为 [4,4,6,6,6,5] 注意&am…...

深入解读财报,开启美股投资之旅
投资股票市场,尤其是美股市场,对于许多投资者来说是一项充满挑战的活动。然而,无论投资者是倾向于技术分析还是基本面分析,财报都是他们不可或缺的工具。本文将带领读者深入了解如何通过阅读和分析财报,发现潜在的投资…...

邦芒支招:成功找到工作要掌握的3个知识点
社会进步,企业商业竞争越来越激烈,不管身为一名职场小白或是想调换一下目前的工作的人,都想找到一个称心如意的好工作。拥有以下三点知识点,可以使我们找到工作。 1、迫不得已,别做这件事 拍桌子说“我不开了”的时候有…...

Educational Codeforces Round 168 (Rated for Div. 2)-7.30复盘
A. Strong Password 简单题,找到相同的两个相邻字母之间插一个跟他们不同的大写字母即可 inline void solve(){cin>>s;int id0;char hh ;for(int i1;i<s.size();i){if(s[i-1]s[i]){idi;break;}} for(int i0;i<26;i){if(s[id]!ai&&s[id1]!ai) …...

Web开发:小结Apache Echarts官网上常用的配置项(前端可视化图表)
目录 一、须知 二、Title 三、 Legend 四、Grid 一、须知 配置项官方文档:点此进入。 我总结了比较常用的功能,写进注释里面,附带链接分享和效果图展示。(更新中....) 二、Title option {title: {text: Weekl…...

B树的平衡性与性能优化
B树的平衡性与性能优化 B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于保持数据的有序性并允许高效的插入、删除和查找操作。B树能够很好地处理大规模数据,并在磁盘I/O操作中表现出色。本文…...

llama3源码解读之推理-infer
文章目录 前言一、整体源码解读1、完整main源码2、tokenizer加载3、llama3模型加载4、llama3测试数据文本加载5、llama3模型推理模块1、模型推理模块的数据处理2、模型推理模块的model.generate预测3、模型推理模块的预测结果处理6、多轮对话二、llama3推理数据处理1、完整数据…...

【教程】Linux安装Redis步骤记录
下载地址 Index of /releases/ Downloads - Redis 安装redis-7.4.0.tar.gz 1.下载安装包 wget https://download.redis.io/releases/redis-7.4.0.tar.gz 2.解压 tar -zxvf redis-7.4.0.tar.gz 3.进入目录 cd redis-7.4.0/ 4.编译 make 5.安装 make install PREFIX/u…...

全球汽车线控制动系统市场规模预测:未来六年CAGR为17.3%
引言: 随着汽车行业的持续发展和对安全性能需求的增加,汽车线控制动系统作为提升车辆安全性和操控性的关键组件,正逐渐受到市场的广泛关注。本文旨在通过深度分析汽车线控制动系统行业的各个维度,揭示行业发展趋势和潜在机会。 【…...

Ubuntu运行深度学习代码,代码随机epoch中断没有任何报错
深度学习运行代码直接中断 文章目录 深度学习运行代码直接中断问题描述设备信息问题补充解决思路问题发现及正确解决思路新问题出现最终问题:ubuntu系统,4090显卡安装英伟达驱动535.x外的驱动会导致开机无法进入桌面问题记录 问题描述 运行深度学习代码…...

只有4%知道的Linux,看了你也能上手Ubuntu桌面系统,Ubuntu简易设置,源更新,root密码,远程服务...
创作不易 只因热爱!! 热衷分享,一起成长! “你的鼓励就是我努力付出的动力” 最近常提的一句话,那就是“但行好事,莫问前程"! 与辉同行的董工说:守正出奇。坚持分享,坚持付出,坚持奉献,…...
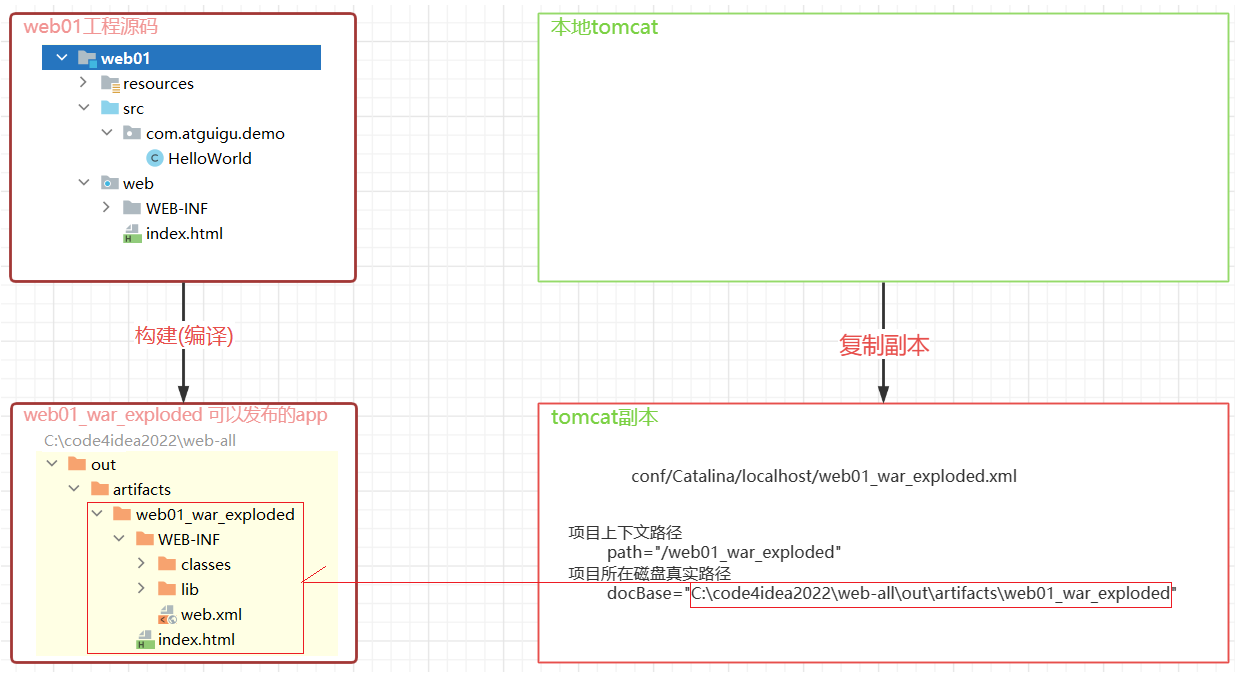
Tomcat部署——个人笔记
Tomcat部署——个人笔记 文章目录 [toc]简介安装配置文件WEB项目的标准结构WEB项目部署IDEA中开发并部署运行WEB项目 本学习笔记参考尚硅谷等教程。 简介 Apache Tomcat 官网 Tomcat是Apache 软件基金会(Apache Software Foundation)的Jakarta 项目中…...

常见且重要的用户体验原则
以下是一些常见且重要的用户体验原则: 1. 以用户为中心 - 深入了解用户的需求、期望、目标和行为习惯。通过用户研究、调查、访谈等方法获取真实的用户反馈,以此来设计产品或服务。 - 例如,在设计一款老年手机时,充分考虑老年…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
