【进阶数据结构】二叉搜索树经典习题讲解
🌈感谢阅读East-sunrise学习分享——[进阶数据结构]二叉搜索树
博主水平有限,如有差错,欢迎斧正🙏感谢有你 码字不易,若有收获,期待你的点赞关注💙我们一起进步
🌈我们在之前已经学习过了二叉树,而如今已经掌握C++语法的我们比起当初只能通过C语言学习已经稍有精进了
C++拥有一些C语言所不具有的优势,所以更适合我们对高阶数据结构的学习,今天要分享的二叉搜索树是二叉树的进阶类型,在做题或实际应用都有着重要地位🚀🚀🚀
目录
- 一、概念
- 二、基本操作
- 2.1 查找
- 2.2 插入
- 2.3 删除
- 三、递归实现
- 3.1 递归查找 - Find
- 3.2 递归插入 - Insert
- 3.3 递归删除 - Erase
- 四、二叉搜索树的应用
- 4.1 K模型
- 4.2 KV模型
- 五、二叉搜索树的性能分析
- 六、二叉树进阶试题
一、概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
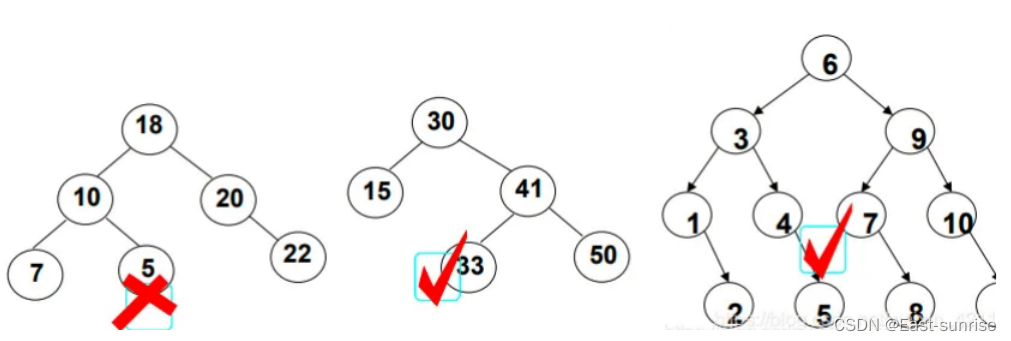
二、基本操作
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ahROcUgG-1679291402813)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316141147146.png)]](https://img-blog.csdnimg.cn/68ed60ee50a74a1e900374789de4f95e.png)
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
2.1 查找
搜索二叉树的特性结构,使得它的查找效率十分快
- 从根开始比较、查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到到空,还没找到,这个值不存在。
✏️代码实现
//查找
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn true;}return false;
}
2.2 插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点
由于要严格遵循二叉搜索树的结构,所以在每次遍历或最后的插入时都需要比较新增节点与其父节点的值的大小♨️所以我们可以用一个parent指针,随时记录下父节点,便于插入时的大小判断💭
✏️代码实现
//插入
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}//插入,小于就插左,大于就插右Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn false;}//到合适的空了,开始插入//要插在左还是右,还是需要比较cur = new Node(key);if (key < parent->_key)parent->_left = cur;if (key > parent->_key)parent->_right = cur;return true;
}
2.3 删除
二叉搜索树的删除较为复杂
首先查找元素是否在二叉搜索树中,如果不存在,则返回false, 否则要删除的结点可能分下面四种情况:
- 要删除的节点无孩子节点
- 要删除的节点只有右孩子节点
- 要删除的节点只有左孩子节点
- 要删除的节点有左、右孩子节点
删除的情况有些许复杂,我们可以将其归成两类
- 直接删除法
- 替换法删除
⭕直接删除法
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-88kdJlGO-1679291402813)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316144712991.png)]](https://img-blog.csdnimg.cn/a82b687e700e4fe3a5a9534979cdc0b7.png)
直接删除法适用于以上的情况1、2、3;其具体情况是删除的节点只有一个孩子或没有孩子节点
而当你删除节点后,其被删节点的孩子节点不能就任其飘荡呀,所以我们就需要对其进行“寄养”;而若删除节点没有孩子节点(左右孩子节点都为空)则删除后,被删节点的父节点所对应的孩子节点也需要指向空🔅
综上所述,根据搜索二叉树的结构可得:
在代码实现时,我们可以把情况1和情况2合为一种情况 —— 被删节点的左孩子节点为空 ——> 判断被删节点为其父节点的左or右孩子 ——> 将被删节点的右孩子与父节点链接起来(寄养)✅
情况3 —— 被删节点的右孩子节点为空 ——> 判断被删节点为其父节点的左or右孩子 ——> 将被删节点的左孩子与父节点链接起来(寄养)✅
🚩🚩直接删除法有一个bug需要留意 —— 当被删节点为根节点时,会出现空指针的问题;因此在代码实现时注意判断
⭕替换法删除
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IMFgd118-1679291402813)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316154547353.png)]](https://img-blog.csdnimg.cn/d724475edc894da294936a8c42b4933a.png)
✏️代码实现
//删除
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//值相等 - 找到了{//1.左为空//2.右为空//3.左右都不为空 - 替换删除if (cur->_left == nullptr){if (cur == _root) //parent == nullptr_root = cur->_right;else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (cur == _root) //parent == nullptr_root = cur->_left;else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{//替换删除Node* parent = cur;Node* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (minRight == parent->_left)parent->_left = minRight->_right;elseparent->_right = minRight->_right;delete minRight;}return true;}}return false;
}
三、递归实现
3.1 递归查找 - Find
bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (key > root->_key)root = root->_right;else if (key < root->_key)root = root->_left;elsereturn true;
}
3.2 递归插入 - Insert
在实现递归插入的过程中,最后会发现插入时需要调用到父指针,但是一步一步传父指针很麻烦💭于是这里用到了一个很巧妙的方法🚩🚩
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fYevGvtg-1679291402813)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316184110286.png)]](https://img-blog.csdnimg.cn/8300e4a66e4241dd9fddc38e7fe2c3f2.png)
✏️代码实现
bool _InsertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}if (key < root->_key)return _InsertR(root->_right, key);else if (key > root->_key)return _InsertR(root->_left, key);elsereturn false;
}
3.3 递归删除 - Erase
✏️代码实现
bool _EraseR(Node*& root, const K& key)
{if (root == nullptr)return false;if (key < root->_key)return _EraseR(root->_left, key);else if (key > root->_key)return _EraseR(root->_right, key);else{//1.左右都为空//2.右为空//3.左右都不为空Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//替换删除Node* minRight = root->_right;while (minRight->_left)minRight = minRight->_left;swap(root->_key, minRight->_key);// 转换成在子树中去删除节点return _EraseR(root->_right, key);}delete del;return true;}
}
此递归实现有两处点睛之笔✨✨
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kHngVX6c-1679291402814)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316185931521.png)]](https://img-blog.csdnimg.cn/b4e72bc8f6734592a81069246abe18f5.png)
🔅假如如图,我们要删除的是节点14,当递归走到节点10这一层时,调用函数时传的是(节点10)-> 右
也就意味着下一层函数的root是10->right的别名;那我们要删除的就是节点正是10 -> right(此时是节点14),我们再创建一个指针del将其存起来;然后直接改变其值 —— root = root -> _left 如此一来,10 -> right 就变为13了✔️最后再将del给delete掉就搞定了
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DVTYGDz1-1679291402814)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230316200627775.png)]](https://img-blog.csdnimg.cn/41baf3a6f539442c9effde75d2bac0a1.png)
当我们需要替换法删除时,替换了节点后,此树子树不符合搜索二叉树的结构了,但是我们能够发现,其删除节点的子树是符合的,因此要删掉节点只需要转换到子树中删除即可✔️
四、二叉搜索树的应用
4.1 K模型
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
4.2 KV模型
KV模型:每一个关键码key,都有与之对应的value,即<Key, Value> 的键值对。这种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
✏️改造二叉搜索树为KV结构
template<class K, class V>
struct BSTNode
{BSTNode(const K& key = K(), const V& value = V()): _pLeft(nullptr) , _pRight(nullptr), _key(key), _Value(value){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;K _key;V _value
};template<class K, class V>
class BSTree
{typedef BSTNode<K, V> Node;typedef Node* PNode;
public:BSTree(): _pRoot(nullptr){}PNode Find(const K& key);bool Insert(const K& key, const V& value)bool Erase(const K& key)
private:PNode _pRoot;
};void TestBSTree3()
{// 输入单词,查找单词对应的中文翻译BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("tree", "树");dict.Insert("left", "左边、剩余");dict.Insert("right", "右边");dict.Insert("sort", "排序");// 插入词库中所有单词string str;while (cin>>str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret == nullptr)cout << "单词拼写错误,词库中没有这个单词:" <<str <<endl;elsecout << str << "中文翻译:" << ret->_value << endl;}
}void TestBSTree4()
{// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的节点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == NULL)countTree.Insert(str, 1);elseret->_value++;}
countTree.InOrder();
}
五、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MDRCgodq-1679291402814)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317102535595.png)]](https://img-blog.csdnimg.cn/e9b74b6618a34a1e948430ef8153c5ee.png)
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:logN
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N/2
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?这就需要我们的AVL树和红黑树派上用场了(后续分享)
✏️附上二叉搜索树源码BST.h
namespace K
{template <class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;//构造函数BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copy(t._root);}~BSTree(){Destroy(_root);_root = nullptr;}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//插入bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}//插入,小于就插左,大于就插右Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn false;}//到合适的空了,开始插入//要插在左还是右,还是需要比较cur = new Node(key);if (key < parent->_key)parent->_left = cur;if (key > parent->_key)parent->_right = cur;return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn true;}return false;}//删除bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//值相等 - 找到了{//1.左为空//2.右为空//3.左右都不为空 - 替换删除if (cur->_left == nullptr){if (cur == _root) //parent == nullptr_root = cur->_right;else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{//替换删除Node* parent = cur;Node* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (minRight == parent->_left)parent->_left = minRight->_right;elseparent->_right = minRight->_right;delete minRight;}return true;}}return false;}//递归bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}//中序遍历void Inorder(){_Inorder(_root);cout << endl;}private:Node* _root = nullptr;Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (key > root->_key)root = root->_right;else if (key < root->_key)root = root->_left;elsereturn true;}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (key < root->_key)return _InsertR(root->_right, key);else if (key > root->_key)return _InsertR(root->_left, key);elsereturn false;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (key < root->_key)return _EraseR(root->_left, key);else if (key > root->_key)return _EraseR(root->_right, key);else{Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{//替换删除Node* minRight = root->_right;while (minRight->_left)minRight = minRight->_left;swap(root->_key, minRight->_key);// 转换成在子树中去删除节点return _EraseR(root->_right, key);}delete del;return true;}}};
}
六、二叉树进阶试题
1️⃣根据二叉树创建字符串
传送门
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-olccb7ug-1679291402815)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317104959288.png)]](https://img-blog.csdnimg.cn/f143b522d23a48a1ac73c15161b6639d.png)
💭解题思路:此题的难点在于括号的省略,我们可以先按照不用省略括号的思路写出前序遍历,再去归纳什么时候就需要省略括号🔅
class Solution {
public:string tree2str(TreeNode* root) {//可能是空树if(root == nullptr)return string();//不是空树,开始前序遍历//首先构造一个stringstring str;//不是空树则先插入根str += to_string(root->val);//前序遍历 - 递归 -- 中-左-右//根完毕后就转换为子问题,去遍历左树,左树完毕就遍历右树//关于括号省略//1.左为空 右为空 - 省略//2.左为空,右不为空 - 不能省略//3.左不为空,右为空 - 省略if(root->left || root->right){str += '(';str += tree2str(root->left);str += ')';}if(root->right){str += '(';str += tree2str(root->right);str += ')';} return str;}
};
2️⃣二叉树的层序遍历
传送门
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jasDUNwz-1679291402815)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317105304078.png)]](https://img-blog.csdnimg.cn/8acc879cfd9048fe9d6bba1dbfb6ab5a.png)
💭解题思路:对于大部分层序遍历,我们都可以利用队列来辅助完成;由于先进先出,每次元素出队列时就带入其子节点,这样我们便能按层顺序入队列以及出队列了。♨️而此题的难点在于不仅要层序遍历,而且还需要将每层的元素分开;那么我们可以在队列加入一个标记变量livesize,来标识每层元素所剩元素个数和是否已经全部出完
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> sum;queue<TreeNode*> q;//有可能是空树if(root == nullptr)return sum;//非空q.push(root);int levesize = 1;while(!q.empty()){vector<int> ret;while(levesize--){TreeNode* front = q.front();q.pop();ret.push_back(front->val);if(front->left)q.push(front->left);eif(front->right)q.push(front->right);}//一层遍历结束levesize = q.size();sum.push_back(ret);}return sum;}
};
3️⃣二叉树的最近公共祖先
传送门
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IVxVQrUg-1679291402815)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317111334729.png)]](https://img-blog.csdnimg.cn/3e1ff0f241084e9bab1c1ce6794a97ce.png)
✏️思路1:递归检查
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wDzPqcHe-1679291402815)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317111401874.png)]](https://img-blog.csdnimg.cn/2fd66c04bfdb47aba520bd8f424c8437.png)
💭解题思路:我们经过分析可以归纳总结以下的情况
1.若有一个根节点,并且一个在其左子树,一个在其右子树,那么此根节点即是最近公共祖先
2.若走到一个节点正是题目中的要求节点之一,而另外一个节点在其子树,则先走到的那个节点为最近公共祖先
- 此思路主要需要判断节点是否在根的左右子树中,因此变量的命名尤为重要,不然就容易乱💤
class Solution {
public:bool Find(TreeNode* sub, TreeNode* x){if(sub == nullptr)return false;if(sub == x)return true;return Find(sub->left, x)|| Find(sub->right, x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)return nullptr;//根就是if(root == q || root == p)return root;bool qInLeft, qInRight, pInLeft, pInRight;pInLeft = Find(root->left, p);pInRight = !pInLeft;qInLeft = Find(root->left, q);qInRight = !qInLeft;//1、一个在左一个在右,root就是最近公共祖先//2、如果都在左,就递归去左边//3、如果都在右,就递归去右边if((pInLeft && qInRight) || (qInLeft && pInRight)){return root;}else if (qInLeft && pInLeft){return lowestCommonAncestor(root->left, p, q);}else if (qInRight && pInRight){return lowestCommonAncestor(root->right, p, q);}else{return nullptr;}}
};
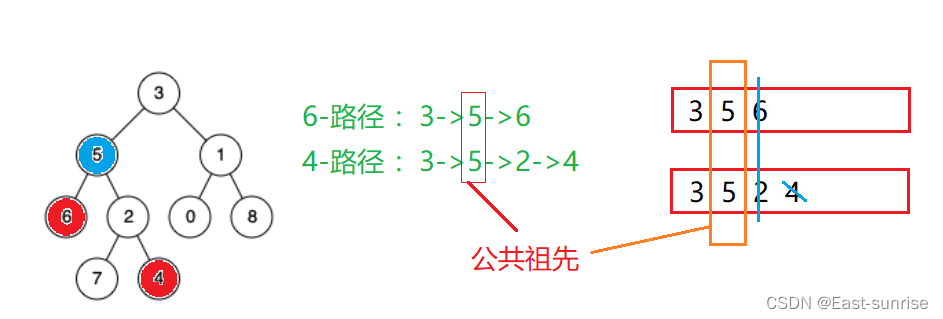
✏️思路2:路径比较
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TbjkRF9q-1679291402815)(C:\Users\DongYu\AppData\Roaming\Typora\typora-user-images\image-20230317114016251.png)]](https://img-blog.csdnimg.cn/8d88dc0e119a480ba818cd182ab6da8a.png)
💭解题思路:从根开始走到每个节点都有其路径,而我们可以把2个节点的路径都记录下来,然后找出那个最后一样的节点便是公共祖先
- 而对于路径的记录我们可以通过递归来记录
- 对于最后公共祖先的查找,我们可以让大的栈先pop,直到两个路径栈的元素个数相同,再相比较,如果不同则pop
class Solution {
public:bool Fpath(TreeNode* root,TreeNode* cur,stack<TreeNode*>& st){if(root == nullptr)return false;st.push(root);if(root == cur)return true;if(Fpath(root->left,cur,st))return true;if(Fpath(root->right,cur,st))return true;//走到光标处说明此节点的左右子树都falsest.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> ppath;stack<TreeNode*> qpath;Fpath(root,p,ppath);Fpath(root,q,qpath);//两个栈的数量不一则要统一//找路径相遇点while(ppath.size()!=qpath.size()){if(ppath.size() > qpath.size())ppath.pop();elseqpath.pop();}while(ppath.top() != qpath.top()){ppath.pop();qpath.pop();}return ppath.top();}
};
🌈🌈写在最后 我们今天的学习分享之旅就到此结束了
🎈感谢能耐心地阅读到此
🎈码字不易,感谢三连
🎈关注博主,我们一起学习、一起进步
相关文章:
【进阶数据结构】二叉搜索树经典习题讲解
🌈感谢阅读East-sunrise学习分享——[进阶数据结构]二叉搜索树 博主水平有限,如有差错,欢迎斧正🙏感谢有你 码字不易,若有收获,期待你的点赞关注💙我们一起进步 🌈我们在之前已经学习…...
PyTorch 之 神经网络 Mnist 分类任务
文章目录一、Mnist 分类任务简介二、Mnist 数据集的读取三、 Mnist 分类任务实现1. 标签和简单网络架构2. 具体代码实现四、使用 TensorDataset 和 DataLoader 简化本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052 一、Mnist 分类任…...

如何实现用pillow库来实现给图片加滤镜?
使用Pillow库可以非常容易地给图片加滤镜。Pillow库是Python图像处理的一个强大库,提供了多种滤镜效果,如模糊、边缘检测、色彩增强等。 下面是使用Pillow库实现给图片加滤镜的简单步骤: 安装Pillow库:首先需要安装Pillow库。可…...
微分中值定理
极值 目录 极值 费马引理 编辑 罗尔定理 拉格朗日中值定理 例题: 例2 例3 两个重要结论: 编辑 柯西中值定理: 如何用自己的语言理解极值呢? 极大值和极小值的类似,我们不再进行说明 极值点有什么特点吗&…...

redis 存储一个map 怎么让map中其中一个值设置过期时间,而不是过期掉整个map?
文章目录 redis 存储一个map 怎么让map中其中一个值设置过期时间,而不是过期掉整个map?Java 中 怎么 实现?方案一: Jedis方案二: Lettuce方案三: Redisson方案四: Jedisson方案五: RedisTemplate那种方式 效率最高 ?拓展:结语redis 存储一个map 怎么让map中其中一个值设置过…...

LeetCode:704. 二分查找
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱704. 二分查找 题目描述:给定一个 n 个元素有序的ÿ…...
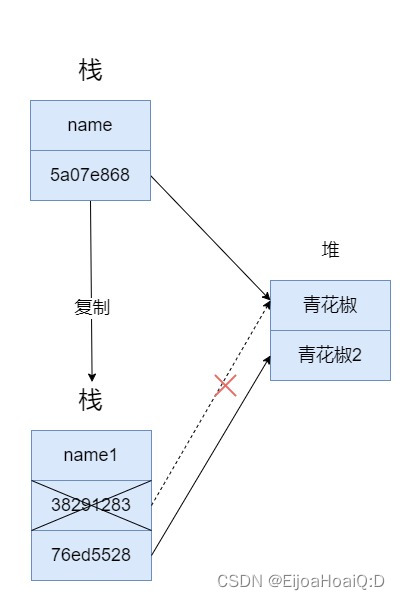
Java 到底是值传递还是引用传递?
C 语言是很多变成语言的母胎,包括 Java。对于 C 语言来说,所有的方法参数都是通过 “值” 传递的,也就是说,传递给被调用方法的参数值存放在临时变量中,而不是存放在原来的变量中。这就意味着,被调用的方法…...
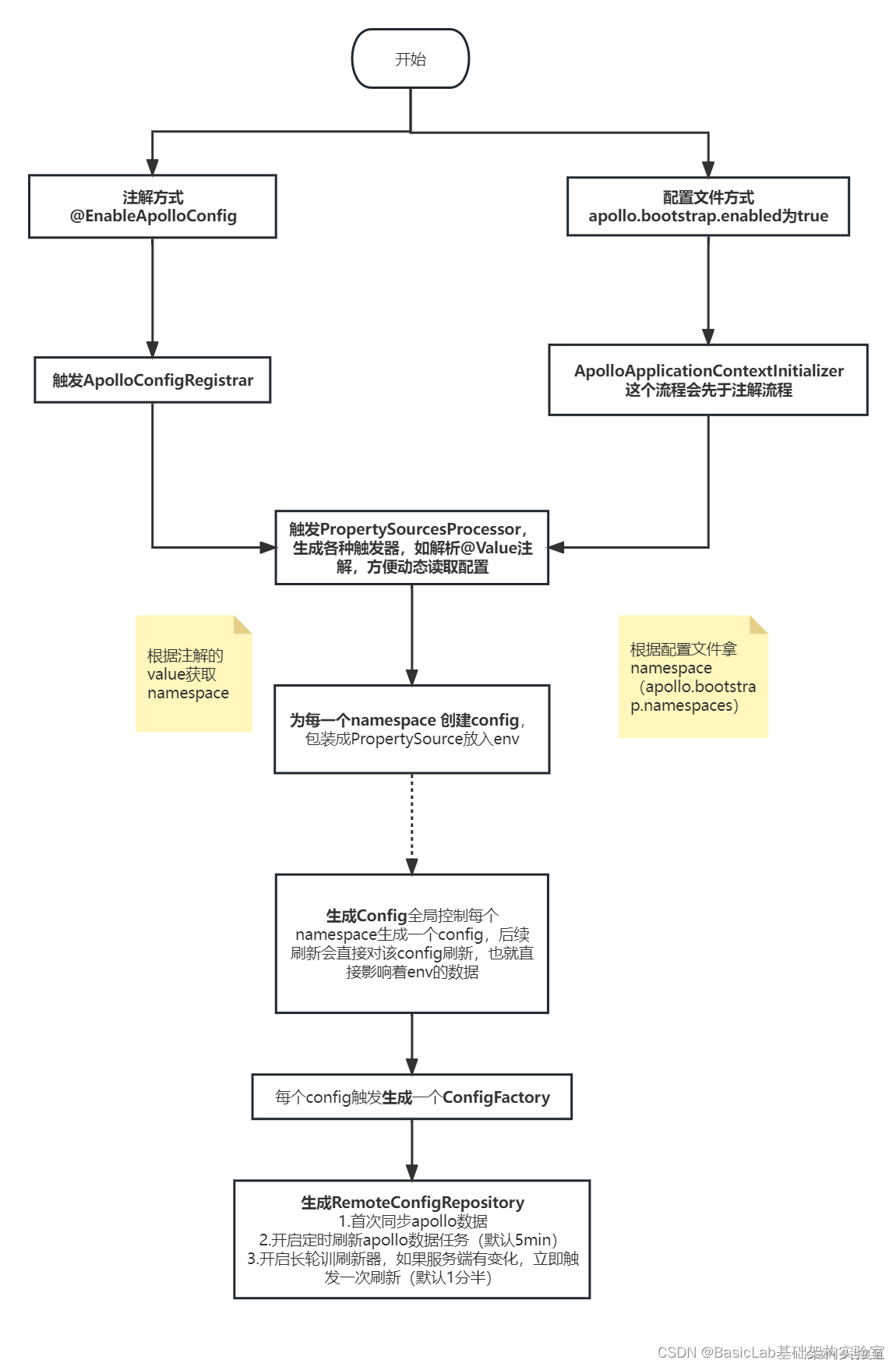
Apollo 配置变更原理
我们经常用到apollo的两个特性:1.动态更新配置:apollo可以动态更新Value的值,也可以修改environment的值。2.实时监听配置:实现apollo的监听器ConfigChangeListener,通过onChange方法来实时监听配置变化。你知道apollo…...
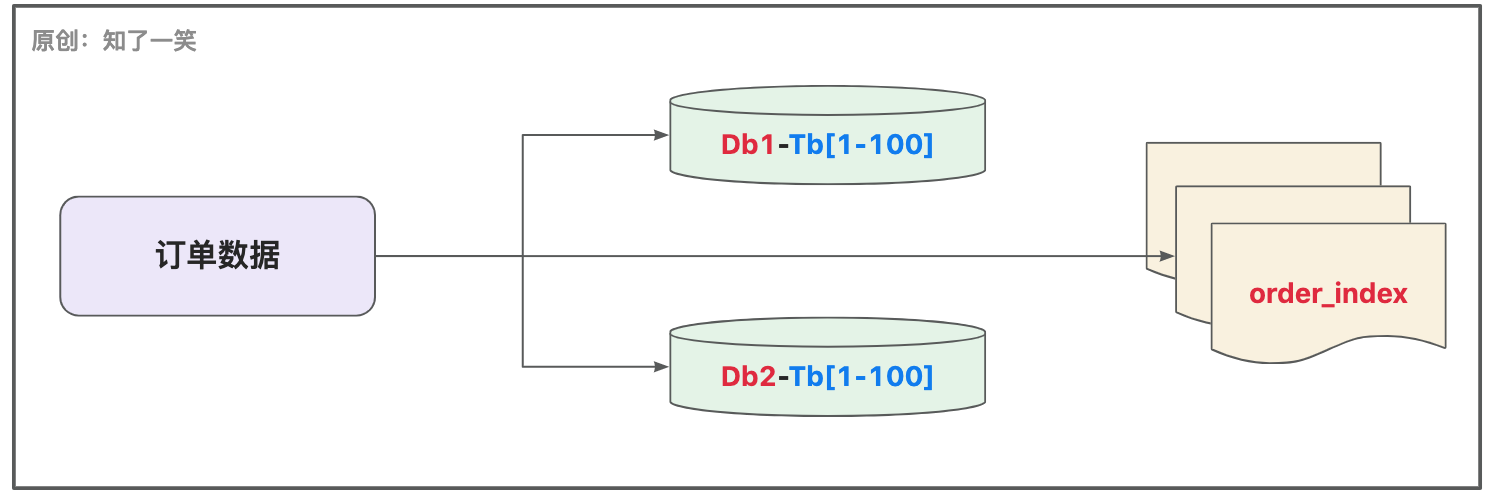
聊聊「订单」业务的设计与实现
订单,业务的核心模块; 一、背景简介 订单业务一直都是系统研发中的核心模块,订单的产生过程,与系统中的很多模块都会高度关联,比如账户体系、支付中心、运营管理等,即便单看订单本身,也足够的复…...

血细胞智能检测与计数软件(Python+YOLOv5深度学习模型+清新界面版)
摘要:血细胞智能检测与计数软件应用深度学习技术智能检测血细胞图像中红细胞、镰状细胞等不同形态细胞并可视化计数,以辅助医学细胞检测。本文详细介绍血细胞智能检测与计数软件,在介绍算法原理的同时,给出Python的实现代码以及Py…...
)
高速PCB设计指南(十五)
掌握IC封装的特性以达到最佳EMI抑制性能 将去耦电容直接放在IC封装内可以有效控制EMI并提高信号的完整性,本文从IC内部封装入手,分析EMI的来源、IC封装在EMI控制中的作用,进而提出11个有效控制EMI的设计规则,包括封装选择、引脚结…...

GPT-4:我不是来抢你饭碗的,我是来抢你锅的
目录 一、GPT-4,可媲美人类 二、它和ChatGPT 有何差别? 01、处理多达2.5万字的长篇内容 02、分析图像的能力,并具有「幽默感」 03、生成网页 三、题外话 四、小结 GPT-4的闪亮登场,似乎再次惊艳了所有人。 看了GPT-4官方的…...

Scala环境安装【傻瓜式教程】
文章目录安装scala环境依赖Java环境安装下载sacla的sdk包安装Scala2.12检查安装是否成功idea配置idea安装scala插件项目配置新建maven项目添加框架支持选择scala创建测试类安装scala环境依赖 Java环境安装 sacla环境安装之前需要先确认Java jdk安装完成 java具体安装步骤略&…...

js实现一个简单的扫雷
目录先看下最终的效果:首先来分析一个扫雷游戏具有哪些功能分析完成后我们就开始一步步的实现1. 相关html和css2. 我们使用类来完成相应功能3. 之后我们则是要定义一个地图4. 对地图进行渲染5. 对开始按钮添加点击事件6. 现在我们可以实现鼠标左击扫雷的功能7. 给单…...
禁用非必需插件,让 IDEA 飞起
文章首发于个人博客,欢迎访问关注:https://www.lin2j.tech IDEA 为我们提供了众多的插件,但是这些插件并不都是必须的。如果电脑的性能不够强,反而会带来一些不必要的资源消耗。 因此这里整理了一些不常用的插件,可以…...
解决win10任何程序打开链接仍然为老旧IE的顽固问题[修改默认浏览器]
文章目录一、问题与修改原因1、着手修改吧2、弯路上探索3、发现祸根二、后话文章原出处: https://blog.csdn.net/haigear/article/details/129344503一、问题与修改原因 我们发现,很多程序默认的网页打开浏览器都是IE,这个很是郁闷ÿ…...

计算机网络体系结构——“计算机网络”
各位CSDN的uu们你们好呀,今天小雅兰来学习一个全新的知识点,就是计算机网络啦,下面,开始虚心学习。 计算机网络的概念 计算机网络的功能 计算机网络的组成 计算机网络的分类 标准化工作 计算机网络的性能 计算机网络的概念 …...
基于微信小程序的校园二手交易平台小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...

Linux lvm管理讲解及命令
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

GPT-4,终于来了!
就在昨天凌晨,OpenAI发布了多模态预训练大模型GPT-4。 这不昨天一觉醒来,GPT-4都快刷屏了,不管是在朋友圈还是网络上都看到了很多信息和文章。 GPT是Generative Pre-trained Transformer的缩写,也即生成型预训练变换模型的意思。…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...
)
Docker环境下安装 Elasticsearch + IK 分词器 + Pinyin插件 + Kibana(适配7.10.1)
做RAG自己打算使用esmilvus自己开发一个,安装时好像网上没有比较新的安装方法,然后找了个旧的方法对应试试: 🚀 本文将手把手教你在 Docker 环境中部署 Elasticsearch 7.10.1 IK分词器 拼音插件 Kibana,适配中文搜索…...
