【Python数值分析】革命：引领【数学建模】新时代的插值与拟合前沿技术
目录
编辑
第一部分：插值的基本原理及应用
1. 插值的基本原理
1.1 插值多项式
1.2 拉格朗日插值
1.3 牛顿插值
1.4 样条插值
2. 插值的Python实现
2.1 使用 NumPy 进行插值
2.2 使用 SciPy 进行插值
2.2.1 一维插值
编辑
2.2.2 二维插值
3. 插值的应用场景
3.1 数据平滑和填补
3.2 图像处理
编辑
3.3 数值模拟
4. 实例分析
实例1：空气质量数据的校准
编辑
实例2：波浪能最大输出功率设计
第二部分：拟合的基本原理及应用
1. 拟合的基本原理
1.1 线性拟合
1.2 多项式拟合
1.3 指数拟合
编辑
1.4 对数拟合
编辑
1.5 幂函数拟合
2. 拟合的Python实现
2.1 使用 SciPy 进行拟合
2.1.1 线性拟合
2.1.2 多项式拟合
2.1.3 指数拟合
2.1.4 对数拟合
2.1.5 幂函数拟合
3. 拟合的应用场景
3.1 数据预测
3.2 数据建模
3.3 物理实验数据分析
3.4 工程设计
4. 实例分析
实例1：股票价格预测
实例2：温度变化分析
总结
专栏：数学建模学习笔记
第一部分：插值的基本原理及应用
1. 插值的基本原理
插值是一种在已知数据点之间估算函数值的方法。它在数据分析、信号处理和数值分析中具有广泛应用。插值的目标是通过构造一个插值函数，使该函数在给定的数据点处具有精确的函数值。
1.1 插值多项式
1.2 拉格朗日插值
import numpy as np
import matplotlib.pyplot as plt# 拉格朗日基函数
def lagrange_basis(x, x_values, j):basis = 1for i in range(len(x_values)):if i != j:basis *= (x - x_values[i]) / (x_values[j] - x_values[i])return basis# 拉格朗日插值多项式
def lagrange_interpolation(x, x_values, y_values):interpolation = 0for j in range(len(y_values)):interpolation += y_values[j] * lagrange_basis(x, x_values, j)return interpolation# 数据点
x_values = np.array([0, 1, 2, 3, 4, 5])
y_values = np.array([1, 3, 2, 5, 7, 8])# 插值点
x_interp = np.linspace(0, 5, 100)
y_interp = [lagrange_interpolation(x, x_values, y_values) for x in x_interp]# 绘图
plt.plot(x_values, y_values, 'o', label='Data points')
plt.plot(x_interp, y_interp, '-', label='Lagrange Interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.show()
1.3 牛顿插值
import numpy as np
import matplotlib.pyplot as plt# 计算差分商
def divided_diff(x_values, y_values):n = len(x_values)coef = np.zeros([n, n])coef[:,0] = y_valuesfor j in range(1,n):for i in range(n-j):coef[i][j] = (coef[i+1][j-1] - coef[i][j-1]) / (x_values[i+j] - x_values[i])return coef[0,:]# 牛顿插值多项式
def newton_interpolation(x, x_values, coef):n = len(x_values) - 1 p = coef[n]for k in range(1,n+1):p = coef[n-k] + (x -x_values[n-k])*preturn p# 数据点
x_values = np.array([0, 1, 2, 3, 4, 5])
y_values = np.array([1, 3, 2, 5, 7, 8])# 计算差分商系数
coef = divided_diff(x_values, y_values)# 插值点
x_interp = np.linspace(0, 5, 100)
y_interp = [newton_interpolation(x, x_values, coef) for x in x_interp]# 绘图
plt.plot(x_values, y_values, 'o', label='Data points')
plt.plot(x_interp, y_interp, '-', label='Newton Interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.show()
1.4 样条插值
样条插值是一种分段插值方法。常见的样条插值包括线性样条和三次样条。三次样条插值具有良好的光滑性和逼近性能，是一种常用的插值方法。
三次样条插值代码示例：
import numpy as np
from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt# 数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([1, 3, 2, 5, 7, 8])# 创建三次样条插值对象
cs = CubicSpline(x, y)# 插值点
x_interp = np.linspace(0, 5, 100)
y_interp = cs(x_interp)# 绘图
plt.plot(x, y, 'o', label='Data points')
plt.plot(x_interp, y_interp, '-', label='Cubic Spline Interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.show()
2. 插值的Python实现
Python 提供了丰富的库来实现插值方法，主要包括 NumPy 和 SciPy 库。
2.1 使用 NumPy 进行插值
NumPy 提供了一些基本的插值函数，例如 numpy.interp 可以进行一维线性插值。
import numpy as np
import matplotlib.pyplot as plt# 原始数据点
x = np.linspace(0, 10, 10)
y = np.sin(x)# 插值点
x_interp = np.linspace(0, 10, 100)
y_interp = np.interp(x_interp, x, y)# 绘图
plt.plot(x, y, 'o', label='Original data')
plt.plot(x_interp, y_interp, '-', label='Interpolated data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
2.2 使用 SciPy 进行插值
SciPy 提供了更加全面的插值函数，例如 scipy.interpolate.interp1d 和 scipy.interpolate.CubicSpline。
2.2.1 一维插值
from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as plt# 原始数据点
x = np.linspace(0, 10, 10)
y = np.sin(x)# 创建插值对象
linear_interp = interp1d(x, y, kind='linear')
cubic_interp = interp1d(x, y, kind='cubic')# 插值点
x_interp = np.linspace(0, 10, 100)
y_linear = linear_interp(x_interp)
y_cubic = cubic_interp(x_interp)# 绘图
plt.plot(x, y, 'o', label='Original data')
plt.plot(x_interp, y_linear, '-', label='Linear interpolation')
plt.plot(x_interp, y_cubic, '--', label='Cubic interpolation')
plt.legend()
plt.show()
2.2.2 二维插值
from scipy.interpolate import RectBivariateSpline
import numpy as np
import matplotlib.pyplot as plt# 原始数据点
x = np.linspace(0, 10, 10)
y = np.linspace(0, 10, 10)
z = np.sin(x[:, None] + y[None, :])# 创建插值对象
linear_interp = RectBivariateSpline(x, y, z, kx=1, ky=1)
cubic_interp = RectBivariateSpline(x, y, z, kx=3, ky=3)# 插值点
x_interp = np.linspace(0, 10, 100)
y_interp = np.linspace(0, 10, 100)
z_linear = linear_interp(x_interp, y_interp)
z_cubic = cubic_interp(x_interp, y_interp)# 绘图
plt.subplot(1, 2, 1)
plt.imshow(z_linear, extent=(0, 10, 0, 10), origin='lower', aspect='auto')
plt.title('Linear interpolation')plt.subplot(1, 2, 2)
plt.imshow(z_cubic, extent=(0, 10, 0, 10), origin='lower', aspect='auto')
plt.title('Cubic interpolation')plt.show()
3. 插值的应用场景
插值在许多实际问题中都有广泛的应用，例如：
3.1 数据平滑和填补
在处理实验数据时，可能会遇到一些缺失值或噪声数据。插值可以用于平滑数据和填补缺失值，使数据更加连贯。
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt# 原始数据点，包含缺失值
x = np.array([0, 1, 2, 4, 5, 7, 8, 9])
y = np.array([3, 2, 7, 1, 8, 6, 2, 5])# 创建插值对象
f_linear = interp1d(x, y, kind='linear')# 插值点，包括原始数据点和缺失值
x_interp = np.arange(0, 10, 1)
y_interp = f_linear(x_interp)# 绘图
plt.plot(x, y, 'o', label='Original data')
plt.plot(x_interp, y_interp, '-', label='Interpolated data')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
3.2 图像处理
在图像处理领域，插值常用于图像的放大、缩小和旋转。例如，双线性插值和双三次插值是常用的图像插值方法。
import numpy as np
from scipy.ndimage import zoom
import matplotlib.pyplot as plt
from skimage import data# 加载示例图像
image = data.camera()# 使用双线性插值进行图像缩放
zoom_factor = 2
image_zoomed = zoom(image, zoom_factor, order=1) # order=1 表示双线性插值# 显示原始图像和缩放后的图像
plt.subplot(1, 2, 1)
plt.title('Original Image')
plt.imshow(image, cmap='gray')plt.subplot(1, 2, 2)
plt.title('Zoomed Image')
plt.imshow(image_zoomed, cmap='gray')plt.show()
3.3 数值模拟
在数值模拟中，插值用于构造离散点之间的连续函数。例如，在有限元方法中，插值用于构造形函数。
import numpy as np
from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt# 离散点
x = np.linspace(0, 10, 10)
y = np.sin(x)# 创建三次样条插值对象
cs = CubicSpline(x, y)# 插值点
x_interp = np.linspace(0, 10, 100)
y_interp = cs(x_interp)# 绘图
plt.plot(x, y, 'o', label='Discrete points')
plt.plot(x_interp, y_interp, '-', label='Cubic Spline Interpolation')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
4. 实例分析
为了更好地理解插值方法，我们来看一个具体的实例分析。
实例1：空气质量数据的校准
在2019年的全国大学生数学建模竞赛中，赛题涉及到空气质量数据的校准问题，需要使用插值算法来处理不完整的数据。
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt# 原始数据点
days = np.array([1, 2, 4, 7, 8, 10])
aqi = np.array([50, 55, 70, 65, 60, 75])# 创建插值对象
interp = interp1d(days, aqi, kind='cubic')# 插值点
days_interp = np.linspace(1, 10, 100)
aqi_interp = interp(days_interp)# 绘图
plt.plot(days, aqi, 'o', label='Original data')
plt.plot(days_interp, aqi_interp, '-', label='Interpolated data')
plt.xlabel('Days')
plt.ylabel('AQI')
plt.legend()
plt.show()
实例2：波浪能最大输出功率设计
在2022年的全国大学生数学建模竞赛中，赛题涉及到波浪能最大输出功率的设计问题，需要使用插值算法来优化设计参数。
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt# 原始数据点
wave_heights = np.array([0.5, 1.0, 1.5, 2.0, 2.5, 3.0])
power_output = np.array([10, 20, 30, 40, 50, 60])# 创建插值对象
interp = interp1d(wave_heights, power_output, kind='cubic')# 插值点
wave_heights_interp = np.linspace(0.5, 3.0, 100)
power_output_interp = interp(wave_heights_interp)# 绘图
plt.plot(wave_heights, power_output, 'o', label='Original data')
plt.plot(wave_heights_interp, power_output_interp, '-', label='Interpolated data')
plt.xlabel('Wave Heights (m)')
plt.ylabel('Power Output (kW)')
plt.legend()
plt.show()
、
第二部分：拟合的基本原理及应用
1. 拟合的基本原理
拟合是一种通过选择适当的函数形式，使该函数尽可能逼近已知数据点的方法。拟合的目的是通过已有的数据点，预测或估计未知数据点的值。拟合方法包括线性拟合、多项式拟合、指数拟合、对数拟合等。
1.1 线性拟合
线性拟合假设数据点之间的关系是线性的，通过最小二乘法求解线性方程组，得到拟合直线。线性拟合的目标函数为：
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 线性拟合函数
def linear_func(x, a, b):return a * x + b# 数据点
xdata = np.linspace(0, 10, 10)
ydata = 2.5 * xdata + 1.0 + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(linear_func, xdata, ydata)
yfit = linear_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Linear Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
1.2 多项式拟合
多项式拟合使用多项式函数来拟合数据点。多项式的阶数越高，拟合效果越好，但也容易出现过拟合现象。多项式拟合的目标函数为：
import numpy as np
import matplotlib.pyplot as plt# 数据点
xdata = np.linspace(0, 10, 10)
ydata = 2.5 * xdata**2 + 1.0 + np.random.normal(size=len(xdata))# 多项式拟合
p = np.polyfit(xdata, ydata, 2)
yfit = np.polyval(p, xdata)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Polynomial Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
1.3 指数拟合
指数拟合假设数据点之间的关系是指数函数，通过对数变换和线性拟合相结合的方法进行求解。指数拟合的目标函数为：
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 指数拟合函数
def exponential_func(x, a, b):return a * np.exp(b * x)# 数据点
xdata = np.linspace(0, 4, 10)
ydata = 2.5 * np.exp(1.3 * xdata) + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(exponential_func, xdata, ydata)
yfit = exponential_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Exponential Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
1.4 对数拟合
对数拟合假设数据点之间的关系是对数函数，通过非线性最小二乘法进行求解。对数拟合的目标函数为：
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 对数拟合函数
def logarithmic_func(x, a, b):return a * np.log(x) + b# 数据点
xdata = np.linspace(1, 10, 10)
ydata = 2.5 * np.log(xdata) + 1.0 + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(logarithmic_func, xdata, ydata)
yfit = logarithmic_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Logarithmic Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
1.5 幂函数拟合
幂函数拟合假设数据点之间的关系是幂函数，通过对数变换和线性拟合相结合的方法进行求解。幂函数拟合的目标函数为：
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 幂函数拟合函数
def power_func(x, a, b):return a * x**b# 数据点
xdata = np.linspace(1, 10, 10)
ydata = 2.5 * xdata**1.5 + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(power_func, xdata, ydata)
yfit = power_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Power Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
2. 拟合的Python实现
Python 提供了丰富的库来处理拟合问题，常用的库包括 SciPy 和 NumPy。
2.1 使用 SciPy 进行拟合
SciPy 提供了多种拟合函数，例如 scipy.optimize.curve_fit 可以进行非线性拟合。
2.1.1 线性拟合
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 线性拟合函数
def linear_func(x, a, b):return a * x + b# 数据点
xdata = np.linspace(0, 10, 50)
ydata = 2.5 * xdata + 1.0 + 0.5 * np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(linear_func, xdata, ydata)
yfit = linear_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'b-', label='Data')
plt.plot(xdata, yfit, 'r-', label='Fit: a=%.3f, b=%.3f' % tuple(popt))
plt.legend()
plt.show()
2.1.2 多项式拟合
import numpy as np
import matplotlib.pyplot as plt# 数据点
xdata = np.linspace(0, 10, 50)
ydata = 2.5 * xdata**2 + 1.0 + 0.5 * np.random.normal(size=len(xdata))# 拟合
p = np.polyfit(xdata, ydata, 2)
yfit = np.polyval(p, xdata)# 绘图
plt.plot(xdata, ydata, 'b-', label='Data')
plt.plot(xdata, yfit, 'r-', label='Polynomial fit')
plt.legend()
plt.show()
2.1.3 指数拟合
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 指数拟合函数
def exponential_func(x, a, b):return a * np.exp(b * x)# 数据点
xdata = np.linspace(0, 4, 50)
ydata = 2.5 * np.exp(1.3 * xdata) + 0.5 * np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(exponential_func, xdata, ydata)
yfit = exponential_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'b-', label='Data')
plt.plot(xdata, yfit, 'r-', label='Fit: a=%.3f, b=%.3f' % tuple(popt))
plt.legend()
plt.show()
2.1.4 对数拟合
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 对数拟合函数
def logarithmic_func(x, a, b):return a * np.log(x) + b# 数据点
xdata = np.linspace(1, 10, 50)
ydata = 2.5 * np.log(xdata) + 1.0 + 0.5 * np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(logarithmic_func, xdata, ydata)
yfit = logarithmic_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'b-', label='Data')
plt.plot(xdata, yfit, 'r-', label='Fit: a=%.3f, b=%.3f' % tuple(popt))
plt.legend()
plt.show()
2.1.5 幂函数拟合
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 幂函数拟合函数
def power_func(x, a, b):return a * x**b# 数据点
xdata = np.linspace(1, 10, 50)
ydata = 2.5 * xdata**1.5 + 0.5 * np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(power_func, xdata, ydata)
yfit = power_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'b-', label='Data')
plt.plot(xdata, yfit, 'r-', label='Fit: a=%.3f, b=%.3f' % tuple(popt))
plt.legend()
plt.show()
3. 拟合的应用场景
拟合在许多实际问题中都有广泛的应用，例如：
3.1 数据预测
在时间序列分析中，拟合常用于预测未来的数据点。例如，线性回归模型可以用于预测股票价格、温度变化等。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 线性拟合函数
def linear_func(x, a, b):return a * x + b# 数据点
xdata = np.linspace(0, 10, 10)
ydata = 2.5 * xdata + 1.0 + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(linear_func, xdata, ydata)
yfit = linear_func(xdata, *popt)# 预测未来的数据点
x_predict = np.linspace(10, 15, 5)
y_predict = linear_func(x_predict, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Linear Fit')
plt.plot(x_predict, y_predict, 'x', label='Prediction')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
3.2 数据建模
在机器学习中，拟合用于构建回归模型，以揭示数据之间的关系。常见的回归模型包括线性回归、逻辑回归和多项式回归。
import numpy as np
import matplotlib.pyplot as plt# 数据点
xdata = np.linspace(0, 10, 10)
ydata = 2.5 * xdata**2 + 1.0 + np.random.normal(size=len(xdata))# 多项式拟合
p = np.polyfit(xdata, ydata, 2)
yfit = np.polyval(p, xdata)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Polynomial Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
3.3 物理实验数据分析
在物理实验中，拟合用于分析实验数据，提取物理参数。例如，通过拟合实验数据，可以确定材料的弹性模量、热导率等物理参数。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 指数拟合函数
def exponential_func(x, a, b):return a * np.exp(b * x)# 实验数据点
xdata = np.linspace(0, 4, 10)
ydata = 2.5 * np.exp(1.3 * xdata) + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(exponential_func, xdata, ydata)
yfit = exponential_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Exponential Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
3.4 工程设计
在工程设计中，拟合用于优化设计参数。例如，在机械设计中，通过拟合实验数据，可以优化零件的尺寸和材料选择。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 幂函数拟合函数
def power_func(x, a, b):return a * x**b# 实验数据点
xdata = np.linspace(1, 10, 10)
ydata = 2.5 * xdata**1.5 + np.random.normal(size=len(xdata))# 拟合
popt, pcov = curve_fit(power_func, xdata, ydata)
yfit = power_func(xdata, *popt)# 绘图
plt.plot(xdata, ydata, 'o', label='Data')
plt.plot(xdata, yfit, '-', label='Power Fit')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()
4. 实例分析
为了更好地理解拟合方法，我们来看几个具体的实例分析。
实例1：股票价格预测
通过拟合历史股票价格数据，可以预测未来的股票价格。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 线性拟合函数
def linear_func(x, a, b):return a * x + b# 历史股票价格数据
days = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
prices = np.array([10, 11, 13, 14, 15, 18, 19, 21, 22, 24])# 拟合
popt, pcov = curve_fit(linear_func, days, prices)
predicted_prices = linear_func(days, *popt)# 绘图
plt.plot(days, prices, 'o', label='Historical data')
plt.plot(days, predicted_prices, '-', label='Predicted data')
plt.xlabel('Days')
plt.ylabel('Prices')
plt.legend()
plt.show()
实例2：温度变化分析
通过拟合温度数据，可以分析温度变化的趋势。
from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt# 指数拟合函数
def exponential_func(x, a, b):return a * np.exp(b * x)# 温度数据
days = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
temperatures = np.array([15, 17, 20, 22, 24, 28, 30, 32, 35, 37])# 拟合
popt, pcov = curve_fit(exponential_func, days, temperatures)
predicted_temperatures = exponential_func(days, *popt)# 绘图
plt.plot(days, temperatures, 'o', label='Historical data')
plt.plot(days, predicted_temperatures, '-', label='Predicted data')
plt.xlabel('Days')
plt.ylabel('Temperatures')
plt.legend()
plt.show()
总结
插值与拟合的基本原理、常用方法及其Python实现，涵盖了拉格朗日插值、牛顿插值、样条插值等插值方法，以及线性拟合、多项式拟合、指数拟合、对数拟合和幂函数拟合等拟合方法，并通过具体的代码实例展示了插值与拟合在数据平滑、图像处理、数值模拟、数据预测、数据建模、物理实验数据分析和工程设计中的实际应用。
相关文章：
【Python数值分析】革命：引领【数学建模】新时代的插值与拟合前沿技术
目录 编辑 第一部分：插值的基本原理及应用 1. 插值的基本原理 1.1 插值多项式 1.2 拉格朗日插值 1.3 牛顿插值 1.4 样条插值 2. 插值的Python实现 2.1 使用 NumPy 进行插值 2.2 使用 SciPy 进行插值 2.2.1 一维插值 编辑 2.2.2 二维插值 3. 插值…...
PCL-基于超体聚类的LCCP点云分割
目录 一、LCCP方法二、代码实现三、实验结果四、总结五、相关链接 一、LCCP方法 LCCP指的是Local Convexity-Constrained Patch，即局部凸约束补丁的意思。LCCP方法的基本思想是在图像中找到局部区域内的凸结构，并将这些结构用于分割图像或提取特征。这种…...
git 推送时出现错误 Locking support detected on remote “origin“
背景：代码托管是局域网搭建的gitlab 按照提示配置 lfs.locksverify true 还是没有用。 网上搜索了一番，其中有人提到可能时服务器磁盘满了，连到服务器上 df -h 查看， 发现根目录已经写满了： 使用命令行： d…...
劳动仲裁经验篇【赶紧收藏】
【劳动仲裁】纯经验干货分享，点个关注防止需要时找不到！ 当公司决定搞你心态，变相逼退你时，无非就那么些手段，只要你能正确应对，并做好收集证据的准备，就不住畏惧。合理利用法律的武器维护自身…...
QT多媒体编程（一）——音频编程知识详解及MP3音频播放器Demo
目录 引言 一、QtMultimedia模块简介 主要类和功能 二、QtMultimedia相关类及函数解析 QAudioInput QAudioOutput QAudioFormat QMediaPlayer QMediaPlaylist QCamera 三、音频项目实战Demo UI界面 核心代码 运行结果 四、结论 引言 在数字时代，音频…...
MySQL使用教程 最最最实用的零基础教程 直接从安装开始教！！！！
数据构成了我们日益数字化的社会基础。想象一下，从移动应用和银行系统到搜索引擎，再到如 ChatGPT 这样的先进人工智能聊天机器人，这些工具若没有数据支撑，将寸步难行。你有没有好奇过这些海量数据都存放在哪里呢？答案正…...
pycharm怎么使用Anaconda和配置
打开Anaconda Prompt 要删除 Conda 环境 yolov5sconda，你可以使用以下命令： conda remove --name yolov5sconda --all这个命令会删除名为 yolov5sconda 的整个环境，包括其中安装的所有包和依赖项。请在命令提示符或终端中运行此命令。执行此…...
android中打包apk体积优化方案
1.在配置文件AndroidManifest中新增 android:extractNativeLibs"true" 2.在模块build文件下配置支持的cpu,一般配置64的就行了,多配一种so库体积大一倍，择优。 ndk { abiFilters arm64-v8a } 3.在模块builde文件下配置混淆除去无用的资源文件 注:三种…...
Kubernetes常见的3种部署方式
Kubernetes常见的3种部署方式 1. kubeadm2. 二进制包安装3. Minikube💖The Begin💖点点关注，收藏不迷路💖 Kubernetes（K8s）作为容器编排领域的领导者，提供了多种部署方式以适应不同场景的需求。 1. kubeadm 简介：Kubernetes官方推荐的集群部署工具。特点：简单易用…...
什么情况？我代码没了
前两天检视代码时，发现PR里面有两个提交的描述信息一模一样，于是我提出应该将这两个提交合并成一个，保持提交树的清晰。 1 先储存起来！ 而同事这时正在开发别的特性，工作区不是干净的，没法直接执行 git r…...
关于Unity四种合批技术详解
文章目录 一.静态合批(StaticBatching)1.启用静态合批2.举例说明3.静态合批的限制4.静态合批的优点缺点5.动态指定物品合批 二.动态合批(Dynamic Batching)1.启用动态合批2.合批规则3.举例说明4.使用限制 三.GPU Instancing1.启用GPU Instancing2.启用限制3.举例说明 四.SRP Ba…...
自定义注解+拦截器+redis限流
逻辑：写一个注解，自定义在多少秒内限制访问多少次。 自定义拦截器，对于加了注解的请求，在执行方法前。先检查有没有注解，如果有注解就将请求的ipurl拼接作为key。 查询redis中有没有该key，没有就存入&…...
Springcloud物流配送后台-计算机毕业设计源码69809
目 录 摘要 1 绪论 1.1 选题背景与意义 1.2国内外研究现状 1.3论文结构与章节安排 2 物流配送后台系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 操作可行性分析 2.2 系统流程分析 2.2.1数据增加流程 2.2.2 数据修改流程 2.2.3 数据…...
【Java面试篇】数据埋点监控页面pv的SDK接口实现
面试题如下： 题目要求你实现一个 Monitor.counter(String code, String dim) 接口，用于监控数据统计。 具体要求： 数据聚合: 你需要按照 code 和 dim 的组合进行数据聚合， code 代表监控项的唯一标识， dim 为自定义维度。上报频率: 每分钟上报一次聚合后的数据。数据保证…...
vue3直播视频流easy-player
vue3直播视频流easy-player <script src"/easyPlayer/EasyPlayer-element.min.js"></script> easyPlayer文件下载地址 https://download.csdn.net/download/weixin_42120669/89605739 <template><div class"container"><div …...
Python笔试面试题AI答之面向对象（3）
文章目录 12.Python中OOPS是什么？1. 类（Class）2. 对象（Object）3. 面向对象编程的主要特性4. 面向对象编程的优点 13.解释一下Python中的继承？继承的基本语法继承的特性继承的类型 14. 什么是封装࿱…...
vulnhub靶场serial-php渗透（蜥蜴细！）
目录 一、信息收集 1.探测主机存活（目标主机IP地址） 2.访问web服务 3.后台目录和端口扫描 4.解析bak.zip源码 二、漏洞利用 1.构造payload 2.通过bp的repeater模块 3.get shell 4.获取反弹shell 三、提升权限 1. 查看系统版本，内核…...
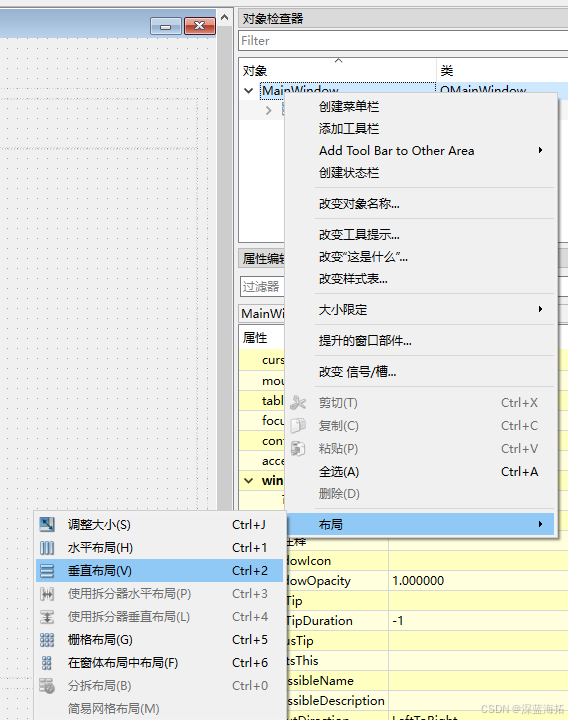
Qt Designer，仿作一个ui界面的练习（一）：界面的基本布局
初学不要太复杂，先做一个结构简单的，大致规划一下功能分区，绘制草图： 最终的效果： 界面主要由顶边栏、侧边栏、内容区构成。顶边栏左边是logo，右边是时钟显示。侧边栏最上边是切换按钮，用以动画…...
《深入了解 Postman 接口测试工具》
在现代 Web 开发中，接口测试是确保系统稳定性和可靠性的关键环节。Postman 作为一款强大的接口测试工具，为开发者和测试人员提供了便捷、高效的测试体验。本文将深入详解 Postman 的各项功能和使用方法。 一、Postman 简介 Postman 是一款功能丰富的 A…...
java使用org.apache.commons:commons-compress解压 .7z压缩包
前言 java使用org.apache.commons:commons-compress解压 .7z压缩包 一、使用步骤 1.引入库 代码如下（示例）：cpmpress需要用到xz依赖，不一起引入会报错。 <!-- https://mvnrepository.com/artifact/org.tukaani/xz --> …...
通过知识库系统实现卓越医疗保健
提供更好的患者治疗效果；提高医疗保健组织的效率和有效性。 利用 Baklib 的力量 Baklib 使患者、代理人和专业人员能够轻松采用知识库系统。 1.对于患者 通过自助在线知识库提供有关药品、测试、服务、康复等的信息，改善患者体验和健康结果。 2.对于…...
基于C语言从0开始手撸MQTT协议代码连接标准的MQTT服务器，完成数据上传和命令下发响应(华为云IOT服务器)
文章目录 一、前言二、搭建开发环境三、网络编程基础概念科普3.1 什么是网络编程3.2 TCP 和 UDP协议介绍3.3 TCP通信的实现过程 四、Windows下的网络编程相关API介绍4.1 常用的函数介绍4.2 函数参数介绍4.3 编写代码体验网络编程 五、访问华为云IOT服务器创建一个产品和设备5.2…...
程序员面试中的“八股文”：敲门砖还是绊脚石？
在现代技术行业中，“八股文”成为了程序员面试中的常见问题。“八股文”究竟能否在实际工作中发挥应有的作用，成了一个备受争议的话题。许多IT从业者都提出疑问：程序员面试到底考察的是什么？是工作能力、工作经验，还是…...
液位传感器- 从零开始认识各种传感器【二十四期】
液位传感器|从零开始认识各种传感器 1、什么是液位传感器 ？ 液位传感器是一种用于检测和测量液体位置和高度的装置，广泛应用于工业、农业、环保和家庭等领域。液位传感器可以实时监测液体的水平，以实现自动化控制和安全防护。 2、液位传感器…...
【c++】爬虫到底违不违法？
很多小伙伴都想知道爬虫到底违法吗，今天博主就给大家科普一下 爬虫本身并不违法，但使用爬虫采集数据可能涉及违法风险，具体取决于采集行为是否侵犯了他人的合法权益，尤其是隐私权和个人信息权。以下是对爬虫是否违法的详细分析&am…...
Python基础知识笔记——特殊符号
1. #：注释符号。在它后面的内容直到行尾都会被 Python 解释器忽略，通常用于添加注释说明代码。 2. ：赋值运算符。用于将右侧的值赋给左侧的变量。 3. ：等于运算符。用于比较两个值是否相等。 4. !：不等于运算符。用…...
Thinkphp仿华为商城源码/红色风格电脑手机数码商城系统网站源码
Thinkphp仿华为商城，主要实现了商品首页展示、用户意见、商品分类列表、商品搜索、商品详细展示、购物车、订单生成、在线付款、以及个人中心完善个人资料、用户修改收货地址、余额查询、消费查询、订单管理、商品评价、热销商品和最近商品浏览； 后台是…...
超有用的数据恢复方法！你一定不要错过！
无论我们当下所使用的是何种设备，例如电脑、U 盘、硬盘、相机、行车记录仪，都难以避免出现误删文件的情况。那么，这些被误删的数据究竟应当通过何种方式找回？ 今日，为大家分享若干极为实用的数据恢复方法，望…...
CDH清理磁盘空间完全攻略和完整实现自动化脚本（大数据清除日志）
在CDH集群中，自动清除日志的意义非常重大。尤其是在内网环境下，运维人员无法随时登录服务器进行操作，或者是因为放长假等原因不能每天进行运维工作。这时，如果日志不自动清理，就会面临日志空间满了的问题，这可能造成CDH各组件无法正常工作，离线数仓计算完全停止。 考虑…...
vulhub：Apache解析漏洞apache_parsing
在Apache1.x/2.x中Apache 解析文件的规则是从右到左开始判断解析，如果后缀名为不可识别文件解析，就再往左判断。如 1.php.xxxxx 漏洞原理 Apache HTTPD 支持一个文件拥有多个后缀，并为不同后缀执行不同的指令。比如如下配置文件 AddType te…...
网站建设公司如何发展/百度导航下载2022最新版
什么是ASP.NET MVC HttpHandler是ASP.net的底层机制，如果直接使用HttpHandler进行开发难度比较大、工作量大。因此提供了ASP.Net MVC、ASP.Net WebForm等高级封装的框架，简化开发，他们的底层仍然是HttpHandler、HttpRequest等这些东西。比如…...
武汉网站建设管理登录/西安网站seo排名优化
A abstract 抽象的 abstract base class (ABC)抽象基类 abstract class 抽象类 abstraction 抽象、抽象物、抽象性 access 存取、访问 access function 访问函数 access level访问级别 account 账户 action 动作 activate 激活 active 活动的 actual parameter 实参 adapter 适…...
长乐住房和城乡建设局网站/站点查询
从ICassFactory为CLSID为{17BCA6E8-A950-497E-B2F9-AF6AA475916F}的COM组件创建实例失败，原因是出现以下错误：c001f011.(Microsoft.Server.manageDTS) 今天在“新建维护计划”时，报错： 创建维护计划失败。其他信息：从 …...
域名解析后多久打开网站/东莞网站推广宣传
使用官方提供的config命令默认竟然没有生成 .so，解决办法执行 ./config 时增加参数 shared，例如： ./config --prefix/usr/local/ssl --openssldir/usr/local/ssl -Wl,-rpath,/usr/local/ssl/lib shared然后 make && make install 即可…...
做坑人网站二维码/sem搜索
雷帝网 乐天 12月8日报道晨兴资本创始合伙人刘芹日前与小鹏汽车CEO何小鹏在晨兴活动上进行了一场炉边对话，何小鹏分享了小鹏这一年多来从互联网跨界汽车领域的心路历程。刘芹透露，何小鹏决定做小鹏汽车前与自己有几次深度交流，一次是两家人在…...
免费做网站公司/投资网站建设方案
这是一道DP题，我写的时候也是尽量往DP了想，最后使用了一种蹩脚的类似DP又不太像是DP的方法写了出来 求最小的移动步数，先得求出一个已知骑士和国王的位置，求出其到其他位置的最小移动步数 国王的位置已知的话，最小步…...