一文弄懂熵、交叉熵和kl散度(相对熵)
一个系统中事件发生的概率越大,也就是其确定性越大,则其包含的信息量越少,可以认为一个事件的信息量就是该事件发生难度的度量,事件所包含的信息量越大则其发生的难度越大。并且相互独立的事件,信息量具有可加性。相互独立的事件的概率具有可乘性,为了使得概率的这种相乘可以和信息量的累加相匹配,所以给事件的概率加上负对数(或者叫做概率倒数的对数),用来定义信息量,而一个系统的平均信息量就叫做这个系统的熵(也叫信息熵),换句话说,一个系统的熵就是这个系统中事件信息量的期望。其中所谓的系统,其实就是包含了一系列随机事件,且随机事件的概率总和为1,在概率论中其实就是我们常说的概率分布。从上可以看出,熵也就是一种特殊的信息量,特殊的地方在于熵只能用来描述系统,而不能用来描述单独的事件。当信息量中的对数的底为2时(其实信息熵是源中的信息量的加权平均,对数的底是默认源中符号总数。一般通信中用到都是bsc(二元对称信道),所以默认取r=2),也称信息熵为理论最小平均编码长度,单位是比特。
具体见下图,其中P为概率分布,H§为分布P的信息熵,:=符号为定义符号,相比于=更加准确,E(Pf)为分布P中所有事件信息量的期望,pi为系统P中某个事件的概率,f(pi)为该事件的信息量。
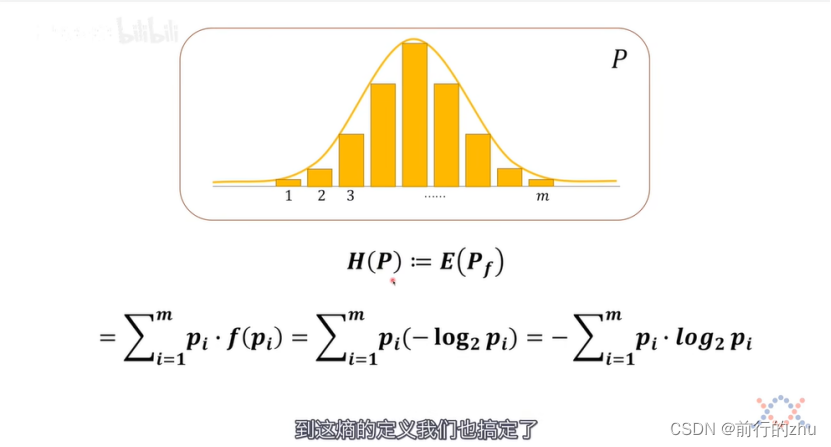
从上可知,可以知道如下的定义推导,事件的概率–>事件的信息量–>概率分布的熵;
需要注意的是,对于同一个事件,其在不同分布出现的概率可能不同,所以对应的信息量也可能不同,记住这一点,在后面将交叉熵的时候有用。
接下来我们来看看相对熵(更常见的叫法是kl散度),为了更加易于理解,下文都叫相对熵,相对熵其实就是度量两个分布熵的差异,既然是比较,那么就需要有一个基准,对于如下的式子DKL(P||Q),就是以P分布为基准,Q分布相对于P分布的相对熵。也可以认为,分布Q距离分布P还需要多少信息量,如果通过某种操作,比如调整分布Q的参数和类型等,将所差的信息量补齐(就是相对熵为0),那么分布Q将和分布P完全一样。具体公式如下:
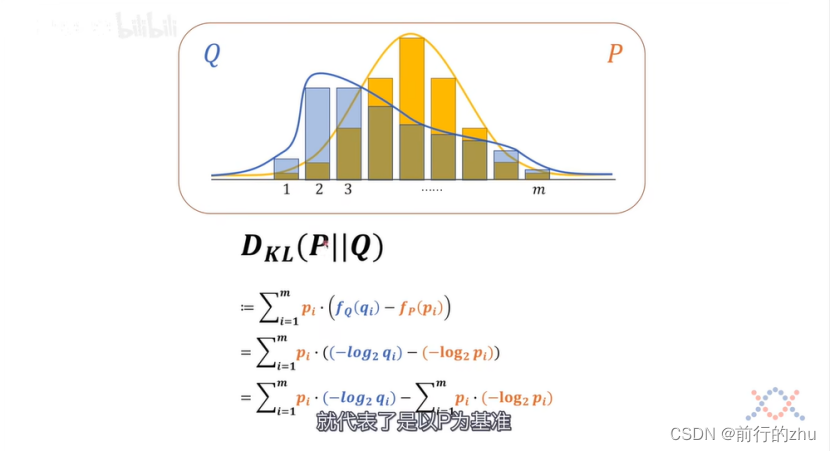
其中,pi为基准分布P中某个事件的概率,fQ(qi)为上述事件在分布Q中的信息量,fp(pi)为上述事件在分布P中的信息量。上述式子经过展开后
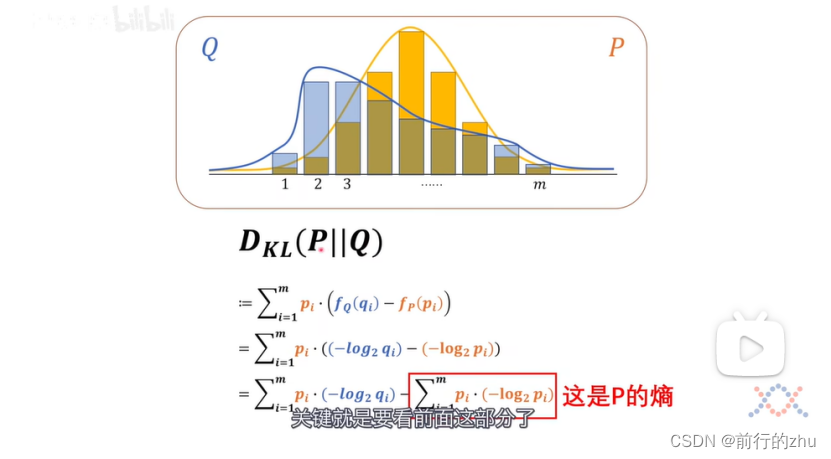
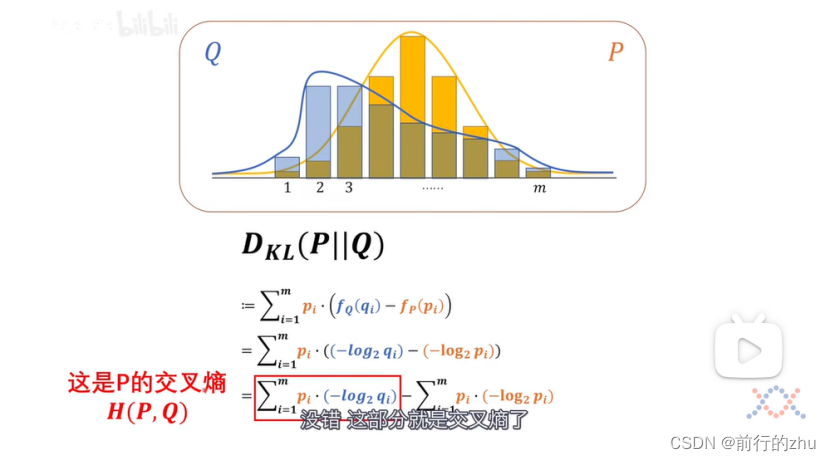
可以看到所谓相对熵其实就等于两个分布的交叉熵减去基准分布的熵。交叉熵为H(P,Q),为P分布和Q分布的交叉熵,为所有基准分布件的概率和该事件在比较分布中对应的信息量的乘积之和。还记得我们上文说的,同一个事件在不同的分布中的概率和信息量可能不同吗?如果任何一个事件在两个分布中的概率和信息量都一样,也就是对于所有的i,pi和qi都一样,则上面式子中的交叉熵H(P,Q)就和基准分布P的熵H(P一样了,也即P和Q的相对熵为0,此时分布P和Q完全一样。
需要注意的是根据吉布斯不等式,两个分布的交叉熵一定大于等于任何一个分布的熵,仅当两个分布一样时等号成立;
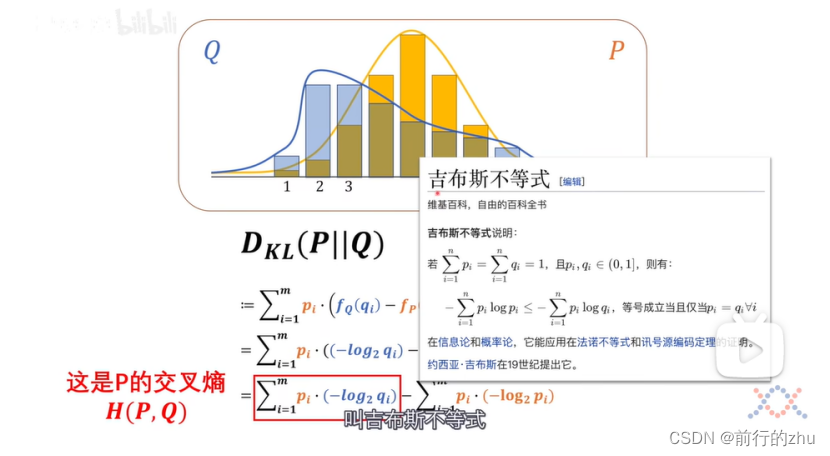
另一个是交叉熵不是对称的,也就是H(P,Q)不等于H(Q,P),同理相对熵也是不对称的。
我们在真实的机器学习算法求损失函数时,实际是以真实分布为基准分布P,我们估计的分布为比较分布Q来计算相对熵,相对熵就是两个分布的“距离”,所以我们使用数据训练模型的目的就是尽可能的使我们的估计分布Q来更接近真实分布P,也就是让相对熵尽可能的小。对于上述相对熵的公式进行求导(对Q分布的参数θ)时,由于真实分布P和θ无关,所以其导数为0,于是便出现了相对熵对θ的导数等于了交叉熵对θ的导数。这也就是我们常说的交叉熵损失函数。
强烈建议结合b站up主的视频进行理解:
“交叉熵”如何做损失函数?打包理解“信息量”、“比特”、“熵”、“KL散度”
【10分钟】了解香农熵,交叉熵和KL散度
相关文章:

一文弄懂熵、交叉熵和kl散度(相对熵)
一个系统中事件发生的概率越大,也就是其确定性越大,则其包含的信息量越少,可以认为一个事件的信息量就是该事件发生难度的度量,事件所包含的信息量越大则其发生的难度越大。并且相互独立的事件,信息量具有可加性。相互…...
10从零开始学Java之开发Java必备软件Intellij idea的安装配置与使用
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者前言壹哥在前面的文章中,带大家下载、安装、配置了Eclipse这个更好用的IDE开发工具,并教会了大家如何在Ecli…...

04 - 进程参数编程
---- 整理自狄泰软件唐佐林老师课程 查看所有文章链接:(更新中)Linux系统编程训练营 - 目录 文章目录1. 问题1.1 再论execve(...)1.2 main函数(默认进程入口)1.3 进程空间概要图1.4 编程实验:进程参数剖析1…...

【python进阶】你真的懂元组吗?不仅是“不可变的列表”
📚引言 🙋♂️作者简介:生鱼同学,大数据科学与技术专业硕士在读👨🎓,曾获得华为杯数学建模国家二等奖🏆,MathorCup 数学建模竞赛国家二等奖🏅,…...
第13章编程练习)
《C++ Primer Plus》(第6版)第13章编程练习
《C Primer Plus》(第6版)第13章编程练习《C Primer Plus》(第6版)第13章编程练习1. Cd类2. 使用动态内存分配重做练习13. baseDMA、lacksDMA、hasDMA类4. Port类和VintagePort类《C Primer Plus》(第6版)第…...
【多线程】多线程案例
✨个人主页:bit me👇 ✨当前专栏:Java EE初阶👇 ✨每日一语:we can not judge the value of a moment until it becomes a memory. 目 录🍝一. 单例模式🍤1. 饿汉模式实现🦪2. 懒汉模…...

【IoT】嵌入式驱动开发:IIC子系统
IIC有三种接口实现方式 三种时序对比: 图1 IIC子系统组成 图2 图3 IIC操作流程 设备端 1.i2c_get_adapter 2.i2c_new_device(相当于register设备) 3.I2c_put_adapter 驱动端 1.填充i2c_driver 2.i2c_add_driver(相当于register驱动) 3.在probe中建立访问方式 client相…...
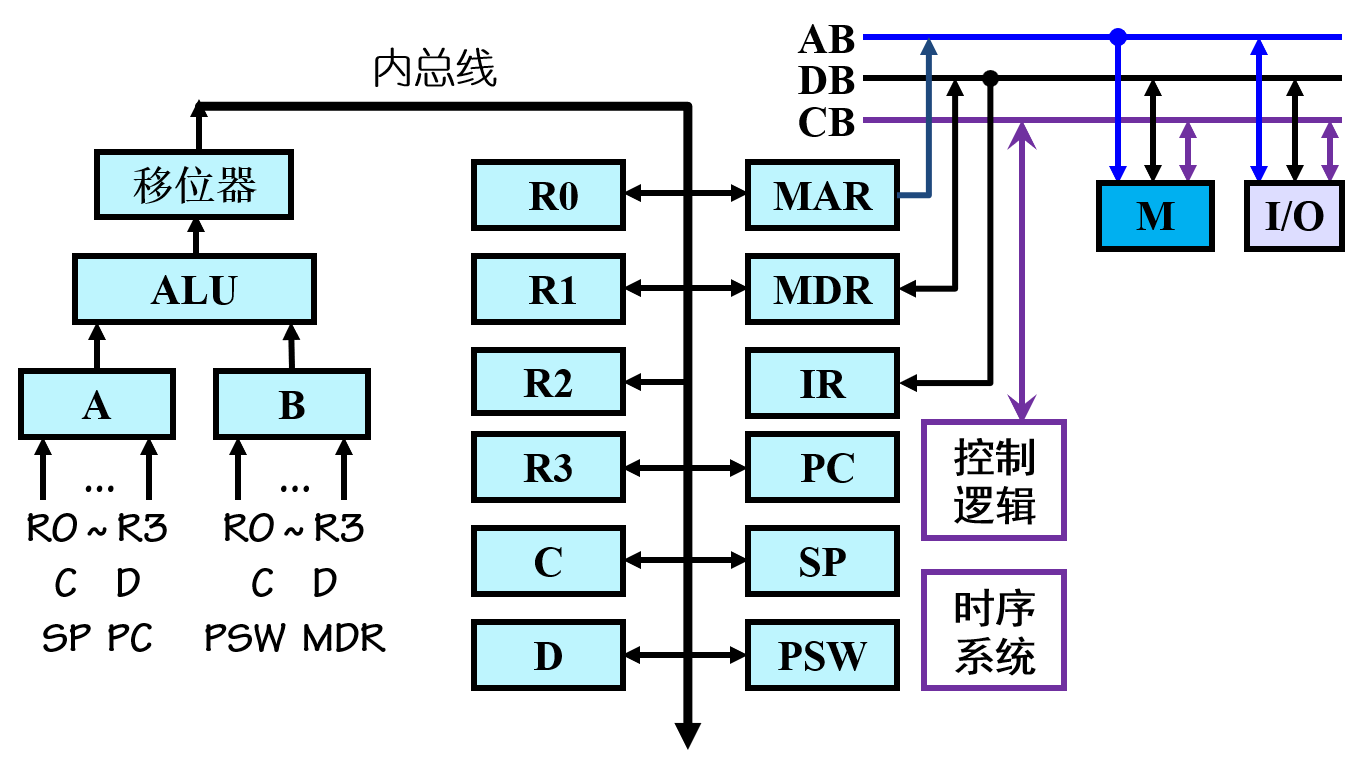
DJ2-4 进程同步(第一节课)
目录 2.4.1 进程同步的基本概念 1. 两种形式的制约关系 2. 临界资源(critical resource) 3. 生产者-消费者问题 4. 临界区(critical section) 5. 同步机制应遵循的规则 2.4.2 硬件同步机制 1. 关中断 2. Test-and-Set …...
AI独立开发者:一周涨粉8万赚2W美元;推特#HustleGPT GPT-4创业挑战;即刻#AIHackathon创业者在行动 | ShowMeAI周刊
👀日报&周刊合辑 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 这是ShowMeAI周刊的第7期。聚焦AI领域本周热点,及其在各圈层泛起的涟漪;拆解AI独立开发者的盈利案例,关注中美AIG…...
不要迷信 QUIC
很多人都在强调 QUIC 能解决 HoL blocking 问题,不好意思,我又要泼冷水了。假设大家都懂 QUIC,不再介绍 QUIC 的细节,直接说问题。 和 TCP 一样,QUIC 也是一个基于连接的,保序的可靠传输协议,T…...

【28】Verilog进阶 - RAM的实现
VL53 单端口RAM 1 思路 简简单单,读取存储器单元值操作即可 2 功能猜想版 说明: 下面注释就是我对模块端口信号 自己猜测的理解。 因为题目并没有说清楚,甚至连参考波形都没有给出。 唉,这就完全是让人猜测呢,如果一点学术背景的人来刷题,指定不容易!! 好在,我有较为…...

【MySQL】聚合查询
目录 1、前言 2、插入查询结果 3、聚合查询 3.1 聚合函数 3.1.1 count 3.1.2 sum 3.1.3 avg 3.1.4 max 和 min 4、GROUP BY 子句 5、HAVING 关键字 1、前言 前面的内容已经把基础的增删改查介绍的差不多了,也介绍了表的相关约束, 从本期开始…...
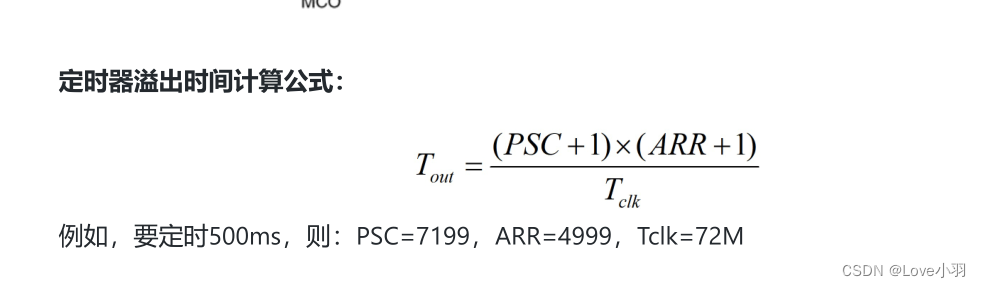
初时STM32单片机
目录 一、单片机基本认知 二、STM系列单片机命名规则 三、标准库与HAL库区别 四、通用输入输出端口GPIO 五、推挽输出与开漏输出 六、复位和时钟控制(RCC) 七、时钟控制 八、中断和事件 九、定时器介绍 一、单片机基本认知 单片机和PC电脑相比…...

debian部署docker(傻瓜式)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 debian10部署dockerdebian10部署docker(傻瓜式)一、准备工作二、**使用 APT 安装,注意要先配置apt网络源**1.配置网络源2.官方下载三、安装…...
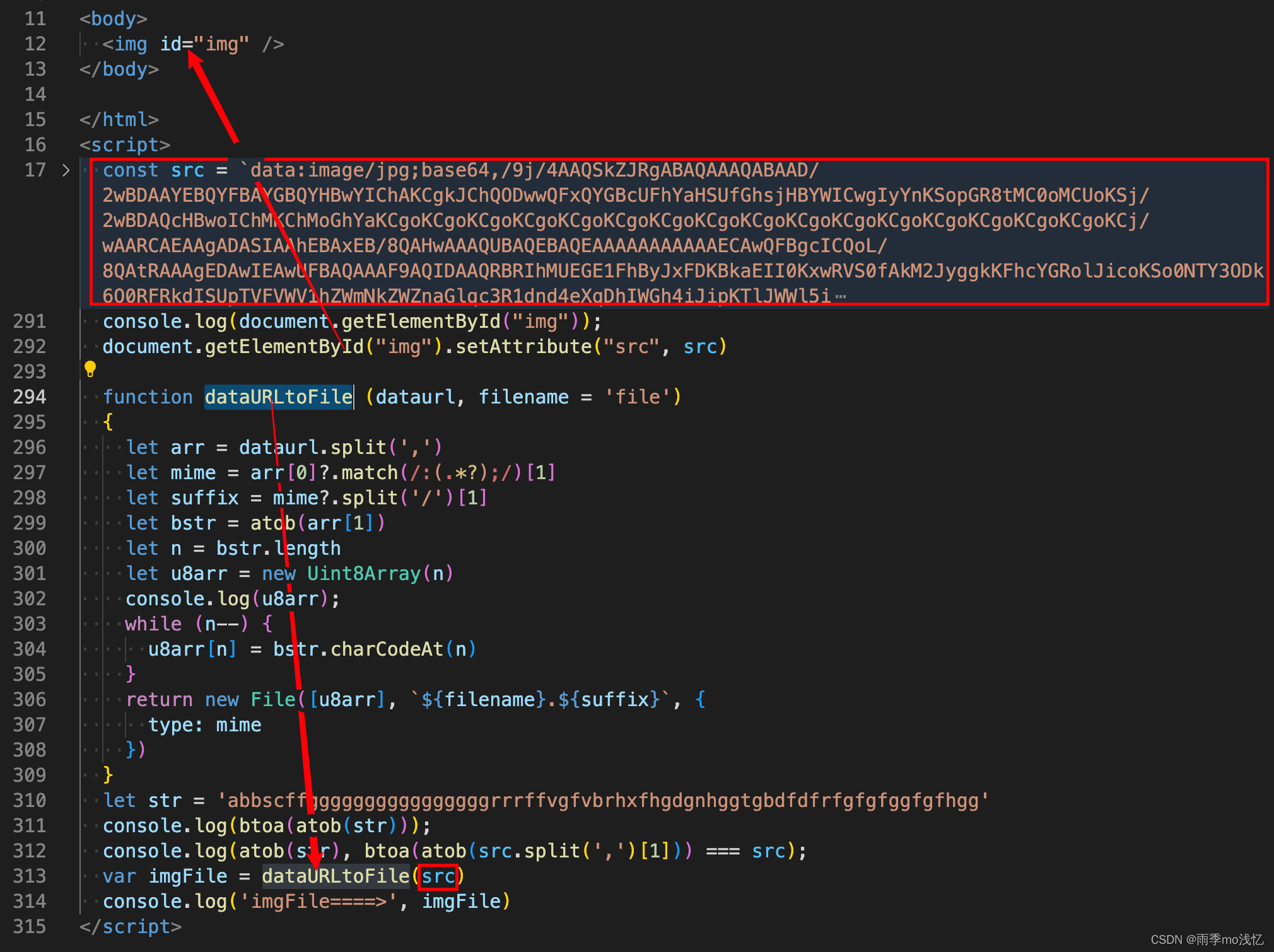
JS判断是否为base64字符串如何转换为图片src格式
需求背景 : 如何判断后端给返回的 字符串 是否为 base-64 位 呢 ? 以及如果判断为是的话,如何给它进行转换为 img 标签可使用的那种 src 格式 呢 ? 1、判断字符串是否为 base64 以下方法,可自行挨个试试,…...

【SpringMVC】SpringMVC方式,向作用域对象共享数据(ModelAndView、Model、map、ModelMap)
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 向域对象共享数据一、使用 原生ServletAPI二、…...
】实验3 - Activity及数据存储)
本科课程【移动互联网应用开发(Android开发)】实验3 - Activity及数据存储
大家好,我是【1+1=王】, 热爱java的计算机(人工智能)渣硕研究生在读。 如果你也对java、人工智能等技术感兴趣,欢迎关注,抱团交流进大厂!!! Good better best, never let it rest, until good is better, and better best. 近期会把自己本科阶段的一些课程设计、实验报…...

为何在 node 项目中使用固定版本号,而不使用 ~、^?
以语雀 文档为准 使用 ~、^ 时吃过亏希望版本号掌握在自己手里,作者自己升级(跟随官方进行升级,就算麻烦作者,也不想麻烦使用者)虽然 pnpm 很好用,但是不希望在项目中用到(临时性解决问题可以选…...
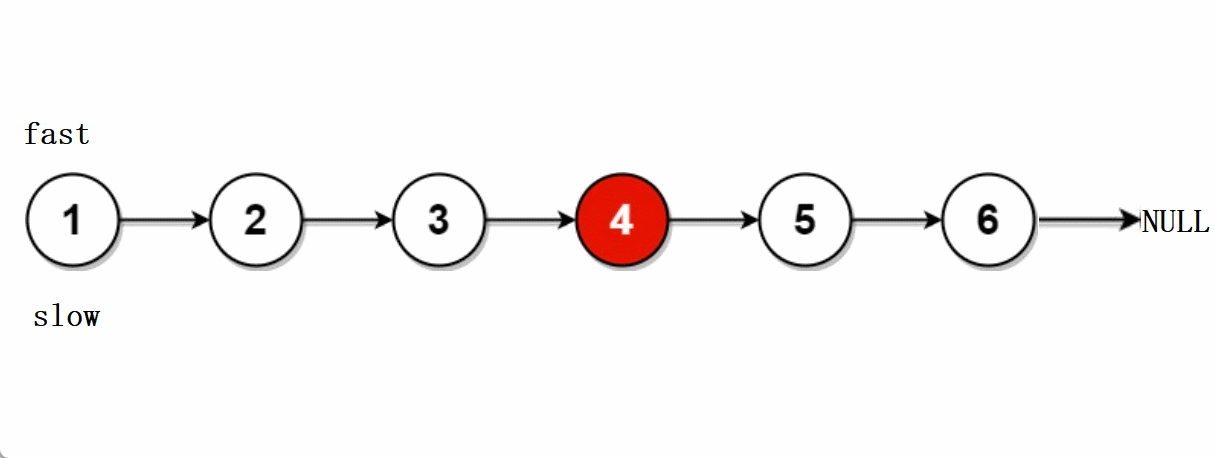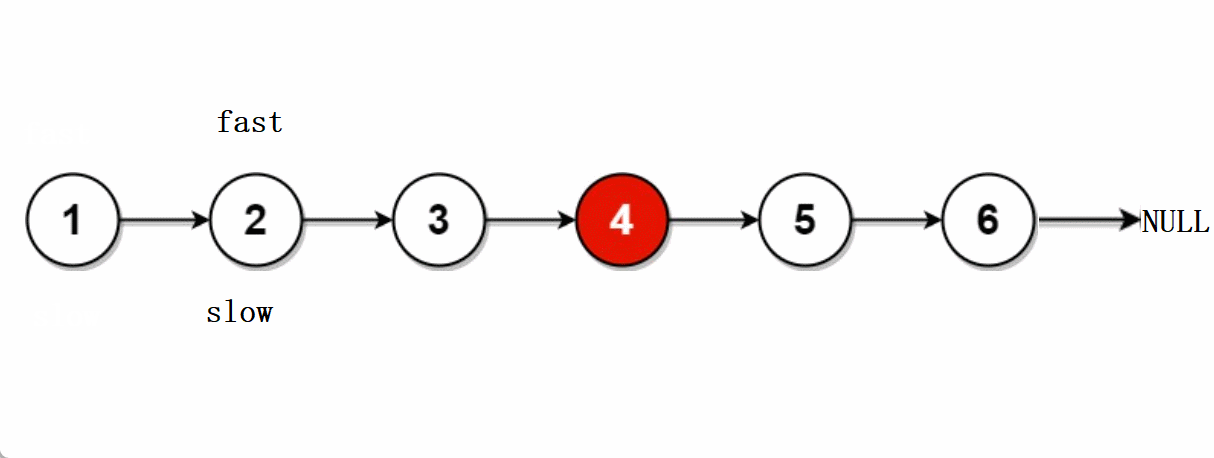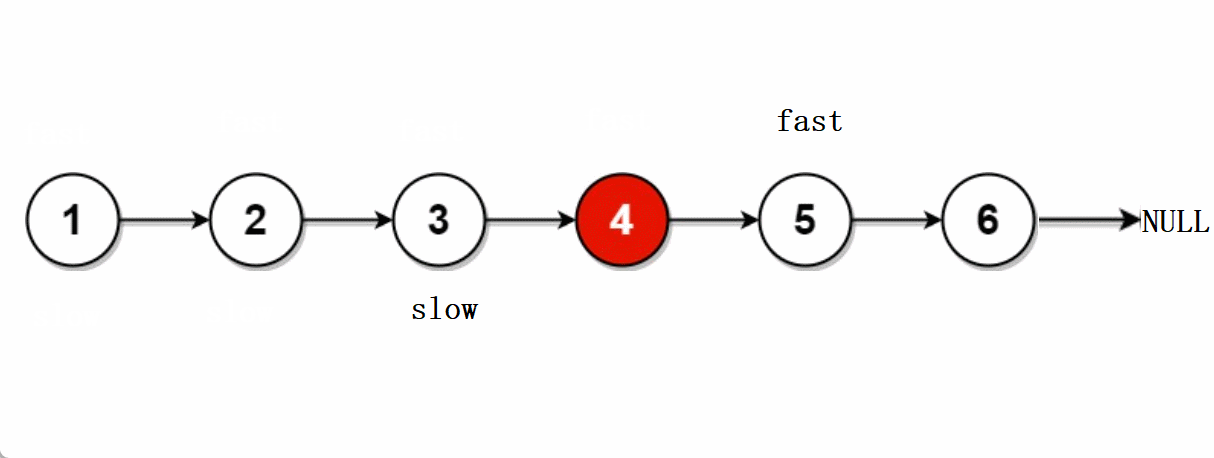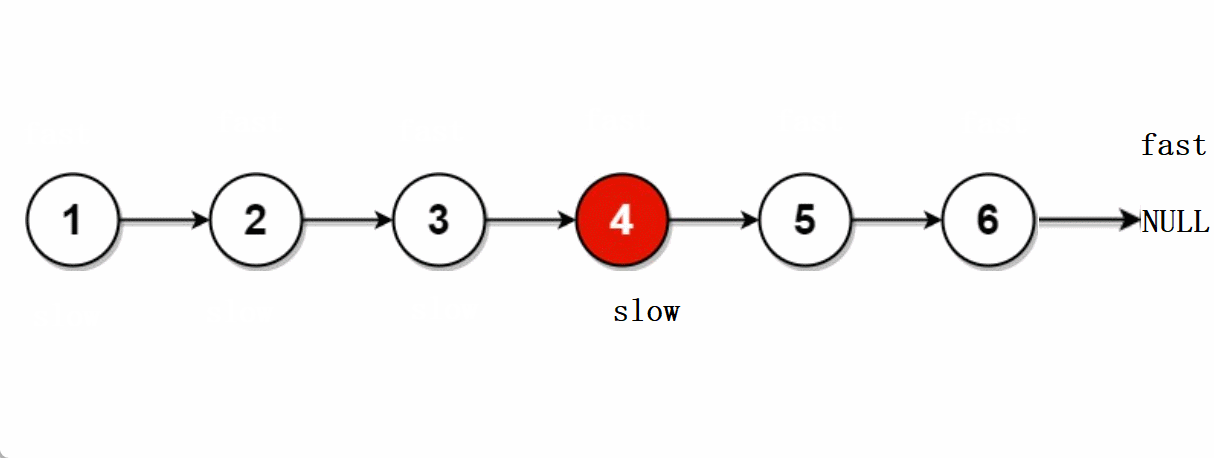
leetcode -- 876.链表的中间节点
文章目录🐨1.题目🐇2. 解法1-两次遍历🍀2.1 思路🍀2.2 代码实现🐁3. 解法2-快慢指针🌾3.1 思路🌾3.2 **代码实现**🐮4. 题目链接🐨1.题目 给你单链表的头结点head&#…...

企业网络安全防御策略需要考虑哪些方面?
随着企业数字化转型的加速,企业网络安全面临越来越多的威胁。企业网络安全不仅仅关乎企业数据的安全,还关系到企业的声誉和利益,因此,建立全面的网络安全防御策略至关重要。 企业网络安全防御策略的实现需要考虑以下几个方面&…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
