动态规划,蒙特卡洛,TD,Qlearing,Sars,DQN,REINFORCE算法对比
动态规划(Dynamic Programming, DP)通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划的步骤
- 识别子问题:定义问题的递归解法,识别状态和选择。
- 确定DP数组:确定存储子问题解的数据结构,通常是数组或矩阵。
- 确定状态转移方程:找出状态之间的关系,即状态转移方程。
- 边界条件:确定DP数组的初始值或边界条件。
- 填表:按照顺序填入DP表,通常是从最小的子问题开始。
- 构造最优解:根据DP表构造问题的最优解。
动态规划与贪心算法的区别
- 贪心算法:在每一步选择局部最优解,希望这能导致全局最优解,但不保证总是得到最优解。
- 动态规划:通过考虑所有子问题的解来构建原问题的最优解,通常能保证得到最优解。
动态规划的局限性
- 时间复杂度:对于某些问题,动态规划的时间复杂度可能很高。
- 空间复杂度:DP算法可能需要大量的存储空间来保存子问题的解。
蒙特卡洛方法用于通过随机模拟来估计和优化策略。
蒙特卡洛方法的关键步骤
- 初始化:初始化价值函数或策略,通常从零或随机值开始。
- 抽样:进行多次实验,每次实验都遵循当前策略进行随机抽样。
- 收集数据:在每次实验中,记录状态、动作、奖励和新状态。
- 更新估计:根据收集的数据更新价值函数或策略的估计。
- 收敛检查:检查估计是否收敛到稳定值,如果是,则停止迭代。
蒙特卡洛方法的特点
- 无需模型:不需要环境的模型信息,适用于模型未知的环境。
- 简单直观:基于随机抽样,方法简单直观。
- 样本效率:随着样本数量的增加,估计的准确性提高。
- 方差问题:由于随机性,估计可能具有较高的方差。
蒙特卡洛方法的局限性
- 计算成本:对于某些问题,可能需要大量的样本才能获得准确的估计。
- 收敛速度:在某些情况下,收敛速度可能较慢。
- 高方差:随机抽样可能导致估计结果的方差较大。
蒙特卡洛方法的变体
- 蒙特卡洛树搜索(MCTS):结合了蒙特卡洛模拟和树搜索的方法,用于决策制定,特别是在游戏AI中。
- 蒙特卡洛梯度策略:结合了蒙特卡洛方法和梯度下降,用于优化策略。
TD(Temporal Difference,时序差分)算法是强化学习中的一种重要算法,它用于估计或学习代理(agent)在环境中采取行动时的价值函数(value function)和策略(policy)。TD学习是一种结合了蒙特卡洛方法和动态规划特点的算法,它不需要模型信息,也不需要完整的episodes来更新其估计。
TD学习的基本思想
TD学习的核心思想是利用时间上相邻的状态-奖励对来估计价值函数。它通过以下步骤实现:
初始化:随机或根据某种策略初始化价值函数 V(s)V(s) 和/或动作价值函数 Q(s,a)Q(s,a)。
迭代更新:在每个时间步 tt,根据当前状态 stst 采取行动 atat,观察奖励 rt+1rt+1 和新状态 st+1st+1,然后根据TD更新规则更新价值函数或动作价值函数。
TD更新公式:
- 对于状态价值函数 VV 的TD(0)更新公式: V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]
- 对于动作价值函数 QQ 的TD(0)更新公式: Q(St,At)←Q(St,At)+α[Rt+1+γmaxaQ(St+1,a)−Q(St,At)]Q(St,At)←Q(St,At)+α[Rt+1+γmaxaQ(St+1,a)−Q(St,At)]
其中:
- αα 是学习率。
- γγ 是折扣因子,决定了未来奖励相对于当前奖励的重要性。
- maxaQ(St+1,a)maxaQ(St+1,a) 是新状态 St+1St+1 下所有可能动作的最大动作价值函数估计。
TD学习的局限性
- 稳定性:TD学习可能在某些情况下不稳定,特别是当学习率较高或折扣因子较大时。
- 收敛性:TD学习可能不会总是收敛到最优解,特别是当策略不是最优的时候。
Q学习(Q-Learning)是一种无模型的强化学习算法,用于学习代理在环境中采取行动时的最优策略。Q学习的核心思想是通过迭代更新来估计每个状态-动作对的价值,即所谓的Q值(Q-values)。Q值代表了在给定状态下采取特定动作的预期回报。
Q学习的关键概念
- Q值(Q(s,a)Q(s,a)):在状态 ss 下采取动作 aa 的预期回报。
- 折扣因子(γγ):一个介于 0 和 1 之间的值,用于平衡即时奖励和未来奖励的重要性。
- 探索(Exploration)和利用(Exploitation):在探索阶段,代理尝试未知的动作以发现更好的策略;在利用阶段,代理使用已知的最佳策略来获得奖励。
Q学习算法的步骤
初始化:为所有状态-动作对 (s,a)(s,a) 初始化 Q 值,通常设置为 0 或小的随机数。
选择动作:在每个时间步 tt,根据当前状态 stst 选择一个动作 atat。这可以通过贪婪策略或ε-贪婪策略来实现,其中ε是探索概率。
执行动作并观察:执行动作 atat,观察奖励 rt+1rt+1 和新状态 st+1st+1。
更新Q值:使用以下公式更新当前状态-动作对的Q值: Q(st,at)←Q(st,at)+α[rt+1+γmaxaQ(st+1,a)−Q(st,at)]Q(st,at)←Q(st,at)+α[rt+1+γmaxaQ(st+1,a)−Q(st,at)] 其中:
- αα 是学习率。
- maxaQ(st+1,a)maxaQ(st+1,a) 是新状态 st+1st+1 下所有可能动作的最大Q值。
移动到新状态:将 stst 更新为 st+1st+1。
重复:重复步骤 2 到 5,直到满足终止条件,如达到最大迭代次数或收敛标准。
Q学习的特点
- 无模型:Q学习不需要环境的模型信息,可以处理未知环境。
- 收敛性:在有限马尔可夫决策过程(MDP)中,Q学习能够收敛到最优策略的Q值,前提是每个状态-动作对都被无限次访问。
- 离策略:Q学习是离策略的,即它可以学习最优策略,即使当前使用的策略不是最优的。
Q学习的局限性
- 维度灾难:当状态空间很大时,Q表可能变得非常大,难以存储和更新。
- 探索问题:需要平衡探索和利用,以避免陷入局部最优。
- 收敛速度:在某些情况下,Q学习可能需要很长时间才能收敛。
Sarsa(State-Action-Reward-State-Action)算法是强化学习中的一种策略学习方法,它与Q学习类似,但主要区别在于Sarsa是在线学习算法,而Q学习是离线学习算法。Sarsa算法学习的是与当前策略一致的价值函数,即它更新的是当前策略下的状态-动作价值函数。
Sarsa算法的关键步骤
初始化:为所有状态-动作对 (s,a)(s,a) 初始化Q值,通常设置为0或小的随机数。
选择动作:在每个时间步 tt,根据当前状态 stst 选择一个动作 atat。这可以通过ε-贪婪策略来实现,其中ε是探索概率。
执行动作并观察:执行动作 atat,观察奖励 rt+1rt+1 和新状态 st+1st+1。
选择下一个动作:在新状态 st+1st+1 下,再次使用当前策略选择下一个动作 at+1at+1。
更新Q值:使用以下公式更新当前状态-动作对的Q值: Q(st,at)←Q(st,at)+α[rt+1+γQ(st+1,at+1)−Q(st,at)]Q(st,at)←Q(st,at)+α[rt+1+γQ(st+1,at+1)−Q(st,at)] 其中:
- αα 是学习率。
- γγ 是折扣因子。
移动到新状态:将 stst 更新为 st+1st+1,并将 atat 更新为 at+1at+1。
重复:重复步骤 2 到 6,直到满足终止条件,如达到最大迭代次数或环境终止。
Sarsa算法的特点
- 在线学习:Sarsa算法在与环境交互的过程中学习,可以适应环境的变化。
- 策略一致性:Sarsa学习的是与当前策略一致的价值函数,即它更新的Q值反映了当前策略下的期望回报。
- 探索与利用:通过ε-贪婪策略,Sarsa算法在探索未知动作和利用已知动作之间取得平衡。
Sarsa算法的局限性
- 探索问题:Sarsa算法需要平衡探索和利用,以避免陷入局部最优。
- 收敛速度:Sarsa算法的收敛速度可能受到当前策略和探索策略的影响。
- 状态空间和动作空间:当状态空间和动作空间很大时,Sarsa算法的学习效率可能会降低。
DQN(Deep Q-Network)算法是由 DeepMind 提出的一种结合了深度学习和 Q 学习(一种强化学习算法)的方法。DQN 解决了传统 Q 学习算法在高维、连续动作空间问题上的局限性,特别是当状态空间非常大时,传统表格型 Q 学习变得不可行。
DQN算法的关键特点:
深度学习:DQN 使用深度神经网络来近似 Q 函数,这使得它可以处理大规模状态空间问题。
经验回放:DQN 引入了经验回放机制,即通过存储过去的转换(状态、动作、奖励、新状态)到一个回放缓冲区,然后随机抽取这些转换来进行训练,这有助于提高数据的利用效率并减少训练过程中的方差。
目标网络:DQN 使用两个相同的神经网络,一个是当前网络,另一个是目标网络。目标网络的参数在每次训练后以较慢的速度更新,这有助于稳定训练过程。
Bellman方程:DQN 通过最大化 Bellman 方程来更新 Q 值,即: Qtarget(s,a)=r+γmaxa′Qtarget(s′,a′)Qtarget(s,a)=r+γmaxa′Qtarget(s′,a′) 其中 QtargetQtarget 是目标网络的 Q 值。
损失函数:DQN 的损失函数是当前 Q 值和目标 Q 值之间的均方差,即: L=E[(y−Q(s,a))2]L=E[(y−Q(s,a))2] 其中 yy 是目标 Q 值。
探索:DQN 通常使用ε-贪婪策略进行探索,即大多数时候选择当前最优动作,但有一定概率随机选择动作。
DQN算法的步骤:
- 初始化 Q 网络和目标网络,以及回放缓冲区。
- 在环境中执行一个动作,观察奖励和新状态。
- 将当前状态、动作、奖励和新状态存储到回放缓冲区。
- 从回放缓冲区中随机抽取一批样本。
- 使用这些样本计算当前 Q 网络的输出和目标 Q 网络的输出。
- 计算损失函数,并用它来更新当前 Q 网络的参数。
- 定期更新目标网络的参数。
- 重复步骤 2 到 7,直到满足终止条件。
DQN算法的局限性:
- 计算资源:DQN 需要大量的计算资源来训练深度神经网络。
- 超参数调整:DQN 对超参数敏感,需要仔细调整以获得最佳性能。
- 泛化能力:DQN 在某些情况下可能难以泛化到未见过的状态或动作。
REINFORCE算法是一种基于蒙特卡洛方法的强化学习算法,用于直接从原始数据中学习策略。它由Rich Sutton等人在1999年的论文《Reinforcement Learning Architectures for Animals》中提出。REINFORCE算法的核心是使用梯度上升方法来优化策略,使得预期回报最大化。
REINFORCE算法的关键概念:
- 策略(Policy):在给定状态下选择动作的概率分布。
- 梯度上升:通过增加能够提高回报的策略的概率来优化策略。
- 蒙特卡洛方法:通过多次采样完整的episodes来估计策略的梯度。
REINFORCE算法的步骤:
初始化:随机初始化策略参数或使用均匀分布。
采样:在当前策略下进行多次采样(即完整的episodes),每个采样包括:
- 从环境的初始状态开始。
- 重复执行动作,直到episode结束。
计算回报:对于每个采样的episode,计算其累积回报,即episode中所有奖励的总和。
估计梯度:使用采样的episodes来估计策略的梯度。对于参数化策略 π(a∣s,θ)π(a∣s,θ),梯度可以估计为: ∇θJ(θ)=Eπ[∑t=1T∇θlogπ(at∣st,θ)⋅Gt]∇θJ(θ)=Eπ[∑t=1T∇θlogπ(at∣st,θ)⋅Gt] 其中 GtGt 是时间步 tt 的回报到episode结束的累积折扣回报。
更新策略:使用梯度上升方法更新策略参数: θ←θ+α⋅∇θJ(θ)θ←θ+α⋅∇θJ(θ) 其中 αα 是学习率。
重复:重复步骤2到5,直到策略收敛或达到预定的迭代次数。
REINFORCE算法的特点:
- 直接策略优化:REINFORCE直接优化策略,而不是价值函数。
- 无需模型:不需要环境的模型信息。
- 适用于连续动作空间:REINFORCE适用于连续动作空间的问题。
REINFORCE算法的局限性:
- 高方差:由于蒙特卡洛采样的随机性,REINFORCE算法的估计可能具有高方差。
- 采样效率低:需要大量的episodes来获得准确的梯度估计。
- 探索问题:在某些情况下,策略可能难以探索到所有可能的动作。
算法对比
动态规划(DP)
- 策略类型:离线,需要模型信息。
- 学习方式:通过迭代计算每个状态的价值函数。
- 适用场景:状态空间和动作空间较小,且模型已知。
- 优点:保证找到最优解。
- 缺点:计算量大,不适用于大规模问题。
蒙特卡洛(MC)
- 策略类型:在线或离线,无需模型信息。
- 学习方式:通过多次采样完整的episodes来估计价值函数或策略。
- 适用场景:适用于样本效率较高的问题。
- 优点:简单直观,容易实现。
- 缺点:高方差,需要大量样本,不适用于连续动作空间。
时序差分(TD)
- 策略类型:在线,无需模型信息。
- 学习方式:通过估计状态转移之间的差异来更新价值函数。
- 适用场景:状态空间较大,适合学习价值函数。
- 优点:比MC更样本高效。
- 缺点:可能不稳定,需要仔细选择学习率。
Q学习
- 策略类型:离线,无需模型信息。
- 学习方式:迭代更新状态-动作对的Q值,目标是找到最优策略。
- 适用场景:适用于学习最优策略。
- 优点:收敛到最优策略,适用于大规模状态空间。
- 缺点:需要探索所有状态-动作对,可能存在探索不足。
Sarsa
- 策略类型:在线,无需模型信息。
- 学习方式:学习与当前行为策略一致的价值函数。
- 适用场景:适用于学习与当前策略一致的策略。
- 优点:策略一致性,适用于连续动作空间。
- 缺点:可能需要更多的探索,收敛速度可能较慢。
深度Q网络(DQN)
- 策略类型:离线,无需模型信息。
- 学习方式:使用深度学习来近似Q值函数。
- 适用场景:适用于高维、大规模状态空间和连续动作空间。
- 优点:能够处理复杂问题,性能强大。
- 缺点:需要大量计算资源,超参数敏感。
REINFORCE
- 策略类型:在线,无需模型信息。
- 学习方式:通过直接优化策略参数来学习策略。
- 适用场景:适用于连续动作空间和高维状态空间。
- 优点:直接策略优化,适用于复杂策略空间。
- 缺点:高方差,需要大量采样,可能难以探索。
总结
- 模型依赖性:DP需要环境模型,而其他方法通常不需要。
- 探索需求:MC和REINFORCE可能需要更多的探索,而DP和Q学习可以更专注于利用。
- 样本效率:TD和DQN通常比MC和REINFORCE更样本高效。
- 策略学习:Sarsa和REINFORCE学习与当前策略一致的策略,而Q学习和DP学习最优策略。
- 适用性:DQN特别适合处理具有高维状态空间和连续动作空间的问题。
在这种需要智能体探索地图、避免障碍并达到目标的任务中,一些算法可能比其他算法更适合。以下是一些可能更适合这类任务的算法,以及它们相对于你提到的算法的优势:
深度Q网络(DQN):
- DQN算法结合了深度学习的表征能力和Q学习的决策制定能力,特别适合处理高维观察空间(如图像)的问题。
- 优势:能够处理像素级别的输入,自动提取特征,适用于复杂环境中的路径规划。
A3C(Asynchronous Advantage Actor-Critic):
- A3C是一种异步的Actor-Critic方法,它使用多个并行的智能体来学习一个策略,并通过异步更新提高数据效率和训练速度。
- 优势:适合于需要大量探索的任务,可以加快学习过程,并且有助于缓解一些优化方面的挑战。
PPO(Proximal Policy Optimization):
- PPO是一种策略梯度方法,它通过优化一个目标函数来改进策略,同时保持与旧策略的接近度,从而实现更稳定的策略改进。
- 优势:策略梯度方法可以直接优化预期回报,适合于连续动作空间的任务。
SAC(Soft Actor-Critic):
- SAC算法是一种结合了熵正则化和Actor-Critic框架的方法,它通过最大化一个关于回报和熵的对数比来学习策略。
- 优势:熵正则化鼓励探索,使得SAC在探索和利用之间取得良好的平衡。
HER(Hindsight Experience Replay):
- HER是一种经验回放方法,它通过将失败的经验转换为次优目标来提高学习效率。
- 优势:适用于目标导向的任务,可以通过转换目标来利用未达到原目标的经验。
MBMF(Model-Based Meta-Learning for Reinforcement Learning):
- MBMF是一种基于模型的元学习方法,它通过学习一个快速适应新任务的策略来提高学习效率。
- 优势:适用于任务变化较大的环境,可以快速适应新目标或新环境。
MCTS(Monte Carlo Tree Search):
- MCTS是一种树搜索方法,通过模拟可能的未来路径来选择最优动作。
- 优势:适合于需要前瞻性规划的任务,尤其是在已知环境模型的情况下。
Dyna-Q++:
- Dyna-Q++是TD学习的一种扩展,它结合了蒙特卡洛方法和模型预测控制,通过模拟来加速学习过程。
- 优势:适用于需要快速探索和学习的环境。
深度Q网络(Deep Q-Network, DQN):
- 结合了深度学习的强大特征提取能力和Q学习的决策制定能力,特别适合处理高维感知数据,如图像。
双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic Policy Gradient, TD3):
- 一种改进的策略梯度方法,通过双网络和延迟策略更新减少了在复杂环境中的过估计问题。
软性Actor-Critic(Soft Actor-Critic, SAC):
- 引入熵正则化来鼓励探索,并通过Actor-Critic框架实现稳定和高效的学习。
异步优势Actor-Critic(Asynchronous Advantage Actor-Critic, A3C):
- 通过并行化智能体来提高数据效率和加速训练过程,适合于需要大量探索的任务。
近端策略优化(Proximal Policy Optimization, PPO):
- 一种策略梯度方法,通过优化一个目标函数来改进策略,同时保持与旧策略的接近度。
模型预测控制(Model Predictive Control, MPC):
- 一种基于模型的规划方法,它在每一步都解决一个优化问题,考虑未来预测的轨迹。
路径积分(Path Integral):
- 一种蒙特卡洛方法,通过采样多个轨迹来估计当前策略的改进方向。
HER(Hindsight Experience Replay):
- 一种经验回放方法,通过转换失败经验的目标来提高学习效率。
MBMF(Model-Based Meta-Learning for Reinforcement Learning):
- 一种基于模型的元学习方法,通过学习快速适应新任务的策略来提高学习效率。
MCTS(Monte Carlo Tree Search):
- 一种树搜索方法,通过模拟可能的未来路径来选择最优动作,适用于需要前瞻性规划的任务。
相关文章:

动态规划,蒙特卡洛,TD,Qlearing,Sars,DQN,REINFORCE算法对比
动态规划(Dynamic Programming, DP)通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划的步骤 识别子问题:定义问题的递归解法,识别状态和选择。确定DP数组:确定存储子问题解的数据结构ÿ…...

HarmonyOS开发商城商品详情页
目录 一:功能概述 二:代码实现 三:效果图 一:功能概述 这一节,我们实现商品详情页的开发,具体流程就是在首页的商品列表点击商品跳转到商品详情页面,同时传递参数到该页面,通过参数调用商品详情接口在详情页展示商品的的详情信息。这里我们为了方便返回首页,在最顶…...

OS_操作系统的运行环境
2024.06.11:操作系统的运行环境学习笔记 第3节 操作系统的运行环境 3.1 操作系统引导3.2 操作系统内核3.2.1 内核资源管理3.2.2 内核基本功能 3.3 CPU的双重工作模式3.3.1 CPU处于用户态(目态)3.3.2 CPU处于内核态(管态) 3.4 特权…...

Maven下载和安装(详细版)
前言 Maven 的含义 Maven 是一个 java 项目管理 和构建工具,他可以定义项目结构,项目依托,并使用统一的方式进行自动化构建,是 java项目不可或缺的工具。 Maven 的 优点 1 提供 标准化的项目结构(具体规定了文件的…...

【优秀python大屏案例】基于python flask的前程无忧大数据岗位分析可视化大屏设计与实现
随着大数据和人工智能技术的迅猛发展,数据分析和可视化在各个行业中的应用越来越广泛。特别是在招聘领域,大数据分析不仅能够帮助企业更好地了解市场需求,还能为求职者提供科学的职业规划建议。本文探讨了基于Python Flask框架的前程无忧大数…...
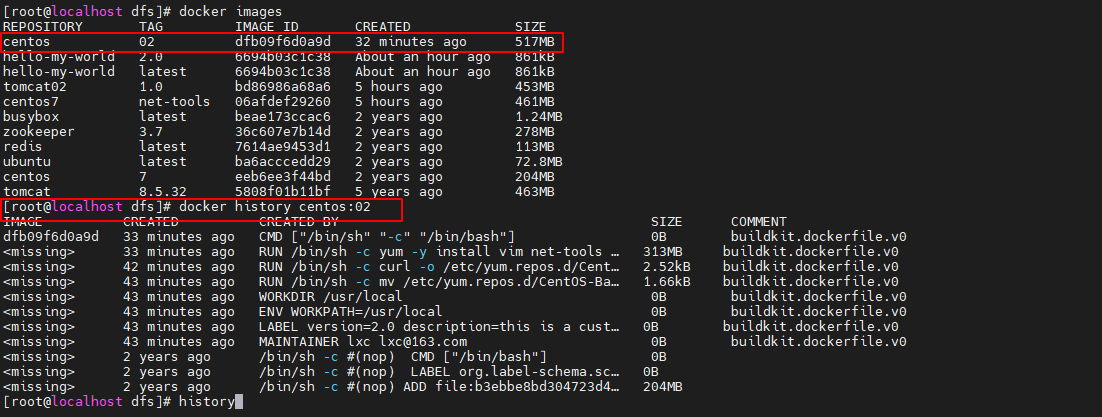
简单的docker学习 第3章docker镜像
第3章 Docker 镜像 3.1镜像基础 3.1.1 镜像简介 镜像是一种轻量级、可执行的独立软件包,也可以说是一个精简的操作系统。镜像中包含应用软件及应用软件的运行环境。具体来说镜像包含运行某个软件所需的所有内容,包括代码、库、环境变量和配置文件等…...

jquery.ajax + antd.Upload.customRequest文件上传进度
前情提要:大文件分片上传,需要利用Upload的customRequest属性自定义上传方法。也就是无法通过给Upload的action属性赋值上传地址进行上传,所以Upload组件自带的上传进度条,也没法直接用了,需要在customRequest中加工一…...

一层5x1神经网络绘制训练100轮后权重变化的图像
要完成这个任务,我们可以使用Python中的PyTorch库来建立一个简单的神经网络,网络结构只有一个输入层和一个输出层,输入层有5个节点,输出层有1个节点。训练过程中,我们将记录权重的变化,并在训练100轮后绘制…...

Project #0 - C++ Primer
知识点 1.pragma once C和C中的一个非标准但广泛支持的预处理指令,用于使当前源文件在单次编译中只被包含一次。 #pragma once class F {}; // 不管被导入多少次,只处理他一次2.explicit C中的一个关键字,它用来修饰只有一个参数的类构造函…...

git提交commit信息规范,fix,feat
可以确保团体合作中,从你的提交记录可以识别出你的动作 feat:新功能(featuer)fix: 修补bugdocs: 文档(documentation)style:格式(修改样式,不影响代码运行的…...

服务器 Linux 的文件系统初探
好久没更新文章了,最近心血来潮,重新开始知识的累计,做出知识的沉淀~ 万事万物皆文件 文件系统:操作系统如何管理文件,内部定义了一些规则或者定义所以在 Linux 中所有的东西都是以文件的方式进行操作在 Linux 中&am…...

关于Unity转微信小程序的流程记录
1.准备工作 1.unity微信小程序转换工具,minigame插件,导入后工具栏出现“微信小游戏" 2.微信开发者工具稳定版 3.MP微信公众平台申请微信小游戏,获得游戏appid 4.unity转webgl开发平台,Player Setting->Other Setting…...

AI入门指南:什么是人工智能、机器学习、神经网络、深度学习?
文章目录 一、前言二、人工智能(AI)是什么?起源概念人工智能分类人工智能应用 三、机器学习是什么?概念机器学习常见算法机器学习分类机器学习与人工智能的关系 四、神经网络是什么?概念神经网络组成部分神经网络模型神经网络和机器学习的关系…...

网络安全中的IOC是指的什么?
网络安全中的IOC(Indicators of Compromise)指的是威胁指标,是网络安全领域中的一个重要概念。它指的是可以用来识别计算机系统、网络或应用程序中已经受到攻击或遭受威胁的特定特征。这些特征可以是恶意文件、恶意域名、已知攻击工具等&…...

掌握AJAX技术:从基础到实战
文章目录 **引言****1. 什么是AJAX?****2. AJAX的工作原理**AJAX 示例使用 Fetch API 实现 AJAX **3. 如何在项目中使用AJAX****4. 处理AJAX请求的常见问题****5. AJAX与JSON的结合****6. 使用AJAX框架和库****7. 实战:创建一个动态表单****8. AJAX中的事…...

Unity UGUI 实战学习笔记(6)
仅作学习,不做任何商业用途 不是源码,不是源码! 是我通过"照虎画猫"写的,可能有些小修改 不提供素材,所以应该不算是盗版资源,侵权删 因为注册和登录面板的逻辑与数据存储方面已经相对完善 服务器面板逻辑…...

iOS面试之属性关键字(二):常见面试题
Q:ARC下,不显式指定任何属性关键字时,默认的关键字都有哪些? 对应基本数据类型默认关键字是:atomic,readwrite,assign 对于普通的 Objective-C 对象:atomic,readwrite,strong Q:atomic 修饰的属性是怎么样保存线程安全的&#x…...

java开发设计模式详解
目录 一、概述 1. 创建型模式(5种) 2. 结构型模式(7种) 3. 行为型模式(11种) 二、代码示例说明 1.单例模式(Singleton) 2.工厂方法模式(Factory Method) 3.抽象工厂模式(Abstract Factory) 4.建造者模式(Builder) 5.原型模式 (Prototype) 6.适…...

windows中node版本的切换(nvm管理工具),解决项目兼容问题 node版本管理、国内npm源镜像切换(保姆级教程,值得收藏)
前言 在工作中,我们可能同时在进行2个或者多个不同的项目开发,每个项目的需求不同,进而不同项目必须依赖不同版本的NodeJS运行环境,这种情况下,对于维护多个版本的node将会是一件非常麻烦的事情,nvm就是为…...
—— APP测试和web测试有什么区别?)
测试面试宝典(四十四)—— APP测试和web测试有什么区别?
一、系统架构和运行环境 APP 测试需要考虑不同的操作系统(如 iOS、Android 等)、设备型号和屏幕尺寸,以及各种网络连接状态(如 2G、3G、4G、WiFi 等)。而 Web 测试主要针对不同的浏览器(如 Chrome、Firefo…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
