算法：BFS 解决多源最短路问题

目录

多源最短路

题目一：矩阵

题目二：飞地的数量

题目三：地图中的最高点

题目四：地图分析

---

多源最短路

首先想要知道多源最短路，就先要明白单源最短路，bfs解决单源最短路问题前面学习过，单源最短路就是只有一个起点，到终点的最短路径

多源最短路就是有若干个起点，到终点的最短路径

多源bfs就是使用bfs解决多源最短路问题

这里再强调一下，能够使用bfs，前提必须是边权为1的问题

多源最短路问题的解决方法：

解法一：暴力枚举

将每一个起点都进行bfs，每个起点都会获得一个结果，得到的这些结果中最小的那一个就是题目所要求的

这种解答大概率是会超时的，所以学习下面的解法二

解法二：把所有的源点当成一个源点

此时问题就变为了单一的单源最短路问题了

在单源最短路问题中，我们是把一个起点加入队列，再一层一层往外扩展

而多源最短路问题中，我们是把所有起点加入队列，再一层一层往外扩展

其实代码都是差不多的，区别就是刚开始的队列加入的起点数目不同

---

题目一：01矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

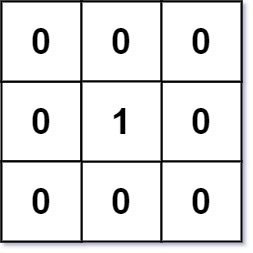
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

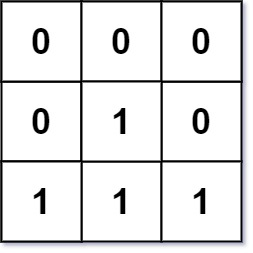
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

---

这道题的题意就是求矩阵中每一个位置的元素的值，每个位置的值是距离最近的0的距离，如果本身就是0，那么距离就是0

解法一：每个位置挨个求

在这种解法中，二维数组的每一个位置依次求离最近的0的距离，很显然是会超时的，所以这种解法就排除了

解法二：多源BFS + 正难则反

因为采用的多源bfs的策略，最初的想法就是将所有的1当做一个起点，去找0，得到最小的距离，但是当找到0后，我们无法得知当前的找到的最短距离是哪个位置的1，所以这种策略是不对的

那么正难则反，我们可以将所有的0当做一个起点，去找1，这样找到的结果和上面也是一样的

那么此时当找到1后，就可以将当前的最短步数直接更新到1的位置上即可，

所以分为下面两步：

1、把所有的0加入到队列中

遍历过程中，所有0位置的数据可以直接更新为0，因为自己本身就是0，距离也就是0

2、一层一层向外扩展

扩展过程中需要注意，已经赋过值的位置就不需要重复赋值了，因为第一次赋值的一定是最短的距离

细节问题：

在前面的单源最短路问题中，我们使用了三个元素来解决，分别是：
记录是否重复出现的bool数组vis
每一次出队列的个数sz
记录扩展了step层，这里的step就是最短路径了

而多源最短路问题，不需要上面的三个元素，只需要一个dist数组即可

因为初始化时，将dist中的值全部初始化为-1，然后将原始值是0的继续改为0，此时再bfs过程中，只要是-1的才改变它的值，这里就不需要使用vis来标记了

并且我们变化是从(a,b)变为(x,y)，当走到(x,y)后，(x,y)的值就是(a,b)的值+1，所以这里也就不需要之前的sz和step了，直接一个dist数组就能解决，dist数组为-1就表示还没有被搜索过，dist不为-1，就表示当前位置的最短距离

当然了此题也是可以使用这三个全局变量，这里只是说明一下，可以更简便的解题

代码如下：

class Solution 
{
public:int dx[4] = {0,0,-1,1};int dy[4] = {-1,1,0,0};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;// 将mat中的0的位置dist该位置也改为0，并将坐标都入队列for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(mat[i][j] == 0){dist[i][j] = 0;q.push({i, j});}}}// 一层一层往外扩while(!q.empty()){// 不需要计算sz，因为dist的值就可以表示走了几步auto [a, b] = q.front();q.pop();int tmp = dist[a][b];for(int k = 0; k < 4; k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = tmp + 1;q.push({x, y});}}}return dist; }
};

---

题目二：飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

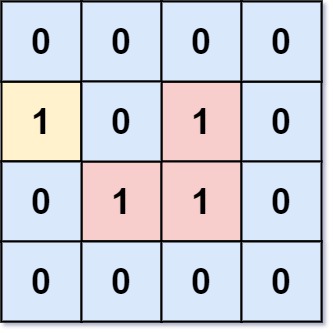
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

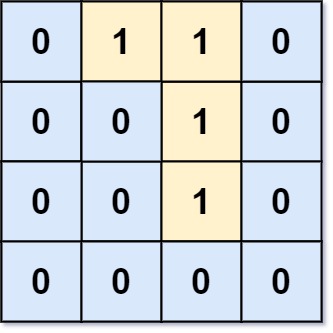
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

---

解法一：暴力解法

在遍历的过程中，找到每一个1，每一个1都去判断，是否能够到达边界

这种解法一定会超时，但是也可以做优化

即找到某一个1时，如果发生这个1能够到达边界，那么此时再遍历一遍，将这个遍历过程中的所有1都做一下标记， 下次就不需要遍历这些做过标记的1了，这种优化可以做到不超时，但是还是有些麻烦的，因为需要bfs两次，下面看解法二

解法二：正难则反

从里面找1到边界需要考虑的事情非常多，但是我可以从边界的所有1开始向里面搜索，此时搜索到的1就一定是可以到达边界的

这种解法使用bfs时，就可以采用多源bfs的方法，将边界所有的1全部添加进队列中，就可以将所有的满足条件的1全部遍历到，最后再找不满足的条件的1的个数即可

代码如下：

class Solution 
{
public:typedef pair<int, int> PII; int dx[4] = {0,0,-1,1};int dy[4] = {-1,1,0,0};bool vis[501][501];int numEnclaves(vector<vector<int>>& g) {int m = g.size(), n = g[0].size();queue<PII> q;// 将边界的1加入队列中for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(g[i][j] == 1 && (i == 0 || i == m - 1 || j == 0 || j == n - 1)){q.push({i, j});vis[i][j] = true;}// 多源 bfswhile(!q.empty()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && g[x][y] == 1 && vis[x][y] == false){q.push({x, y});vis[x][y] = true;}}}// 统计结果int ret = 0;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(g[i][j] == 1 && vis[i][j] == false)ret++;return ret;}
};

---

题目三：地图中的最高点

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

• 如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
• 如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。

你需要按照如下规则给每个单元格安排高度：

• 每个格子的高度都必须是非负的。
• 如果一个格子是 水域 ，那么它的高度必须为 0 。
• 任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

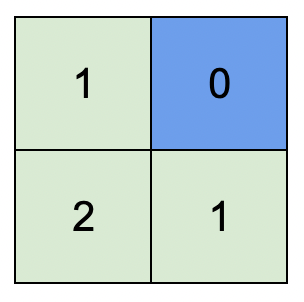
输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

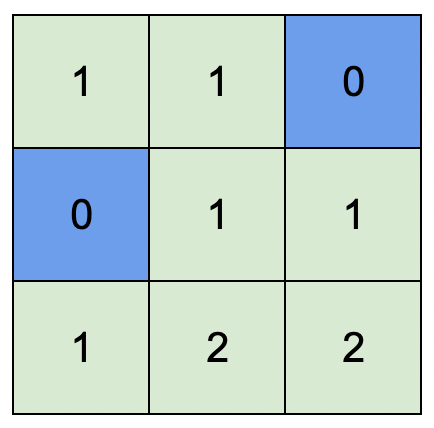
输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

---

这道题的题目描述比较长，其实理解一下就是：

原始矩阵的0表示陆地，1表示水域，需要我们返回一个新矩阵，新矩阵的要求如下：

①原始为水域的位置新矩阵要为0
②其余的位置，每次扩展都可以高度加1
③求整个矩阵的最高高度值

理解完题意，可以看出来，也就是多源bfs，从0位置开始扩展，每次扩展到其他位置时，都+1即可，非常简单

代码如下：

class Solution 
{
public:int dx[4] = {0,0,-1,1};int dy[4] = {-1,1,0,0};typedef pair<int, int> PII;vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {int m = isWater.size(), n = isWater[0].size();vector<vector<int>> height(m, vector<int>(n, -1));queue<PII> q;// 将所有源点(水域)加入队列for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(isWater[i][j] == 1){height[i][j] = 0;q.push({i, j});}// 多源bfswhile(!q.empty()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && height[x][y] == -1){// 每次的高度是之前高度+1height[x][y] = height[a][b] + 1;q.push({x, y});}}}return height;}
};

---

题目四：地图分析

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

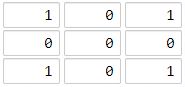
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

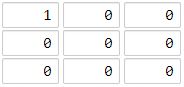
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

---

同样，此题也非常简单，简单分析一下：

0表示海洋，1表示陆地，请找到海洋距离最远的陆地，如果整个矩阵只有海洋或是陆地，就返回-1

这道题的解法和前面几乎一模一样， 找0到1的最大距离，这个并不好找

我们同样正难则反，找1到0的最远距离，每次扩展一层就+1，最后返回最大的值即可

代码如下：

class Solution 
{
public:int dx[4] = {0,0,-1,1};int dy[4] = {-1,1,0,0};typedef pair<int, int> PII;int maxDistance(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<PII> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j] == 1){dist[i][j] = 0;q.push({i, j});}int ret = -1;while(!q.empty()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k];int y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){q.push({x, y});dist[x][y] = dist[a][b] + 1;ret = max(ret, dist[x][y]);}}}return ret;}
};

---

BFS 解决多源最短路问题到此结束