DirectX12(D3D12)基础教程(二十一)—— PBR:IBL 的数学原理(2/5)
目录
- 3、IBL 数学原理
- 3.1、基于微平面理论的 “Cook-Torrance” 模型回顾
- 3.2、 ksk_sks 项与菲涅尔项等价消除
- 3.3、拆分“漫反射项”和“镜面反射项”
3、IBL 数学原理
接下来,就让我们正式进入整个 IBL 的数学原理的旅程。请注意,前方高能!
3.1、基于微平面理论的 “Cook-Torrance” 模型回顾
首先让我们先来完整的复习下整个反射方程(渲染方程):
Lo(p⃗,ωo⃗)=∫Ω(kdcπ+ksDFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗其中:D=NDFGGXTR(n⃗,h⃗,α)=α2π((n⃗⋅h⃗)2(α2−1)+1)2F=FSchlick(h⃗,ωo⃗,F0)=F0+(1−F0)(1−(h⃗⋅ωo⃗))5GSchlickGGX(n⃗,ωo⃗,κ)=n⃗⋅ωo⃗(n⃗⋅ωo⃗)(1−κ)+κκdirect=(α+1)28κIBL=α22G(n⃗,ωo⃗,ωi⃗,κ)=GSchlickGGX(n⃗,ωo⃗,κ)GSchlickGGX(n⃗,ωi⃗,κ)上列式子中:α=roughness2roughness∈[0.0,1.0](粗糙度系数)h⃗=ωo⃗+ωi⃗∣ωo⃗+ωi⃗∣即出射方向与入射方向的中间向量L_o(\vec{p},\vec{\omega_o}) = \int\limits_{\Omega} (k_d \cfrac{c}{\pi} + k_s \cfrac{ D F G }{ 4 (\vec{\omega_o} \cdot \vec{n} )(\vec{\omega_i} \cdot \vec{n})}) L_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} \mathrm{d} \vec{\omega_i} \\[2ex] 其中: \\[2ex] D = NDF_{GGXTR}(\vec{n},\vec{h},\alpha) = \frac{ \alpha^2 }{\pi (( \vec{n} \cdot \vec{h} )^2(\alpha^2 - 1) + 1) ^ 2} \\[2ex] F = F_{Schlick}(\vec{h},\vec{\omega_o},F_0) = F_0 + ( 1 - F_0 )(1 - (\vec{h} \cdot \vec{\omega_o}))^5 \\[2ex] G_{SchlickGGX}(\vec{n},\vec{\omega_o},\kappa) = \frac{\vec{n} \cdot \vec{\omega_o}}{(\vec{n} \cdot \vec{\omega_o})(1-\kappa) + \kappa } \\[2ex] \kappa_{direct} = \frac{(\alpha + 1)^2}{8} \\[2ex] \kappa_{IBL} = \frac{\alpha^2}{2} \\[2ex] G(\vec{n},\vec{\omega_o},\vec{\omega_i},\kappa) = G_{SchlickGGX}(\vec{n},\vec{\omega_o},\kappa) G_{SchlickGGX}(\vec{n},\vec{\omega_i},\kappa) \\[2ex] 上列式子中:\alpha = roughness^2 \qquad roughness \in [ \ 0.0,1.0 \ ] (粗糙度系数) \\[2ex] \vec{h} = \cfrac{ \vec{\omega_o} + \vec{\omega_i} }{ \left| \vec{\omega_o} + \vec{\omega_i} \right| } \qquad 即出射方向与入射方向的中间向量 Lo(p,ωo)=Ω∫(kdπc+ks4(ωo⋅n)(ωi⋅n)DFG)Li(p,ωi)n⋅ωidωi其中:D=NDFGGXTR(n,h,α)=π((n⋅h)2(α2−1)+1)2α2F=FSchlick(h,ωo,F0)=F0+(1−F0)(1−(h⋅ωo))5GSchlickGGX(n,ωo,κ)=(n⋅ωo)(1−κ)+κn⋅ωoκdirect=8(α+1)2κIBL=2α2G(n,ωo,ωi,κ)=GSchlickGGX(n,ωo,κ)GSchlickGGX(n,ωi,κ)上列式子中:α=roughness2roughness∈[ 0.0,1.0 ](粗糙度系数)h=∣ωo+ωi∣ωo+ωi即出射方向与入射方向的中间向量
仔细观察上述方程积分部分,其中的 DFG 部分以及其分母部分,还有入射光函数都与入射点 p⃗\vec{p}p 、入射光 ωi⃗\vec{\omega_i}ωi 、出射光 ωo⃗\vec{\omega_o}ωo 以及隐含的光源颜色和物体表面的漫反射颜色 ccc 等变量相关联,并且这些变量基本都是矢量形式,所以其计算也是非常复杂的。
当然计算复杂主要是从其计算量来说的,即时间复杂度和空间复杂度。但是这些变量以及表达式至少都是可知和可计算的。如果各位有兴趣可以直接将这个积分方程按照其原始表达式按照黎曼和的形式翻译为 Shader 代码,只是每个点可能都需要海量的计算。当然你也可以通过控制黎曼和的数量来使计算量进一步减小,只是最终效果可能会有些惨不忍睹。这也是实时图形学中最永恒的一个话题——在渲染质量与效率之间进行折中。
所以这个方程虽然理论上已经可以编程进行计算了,因为 BRDF 部分的计算我们在之前的教程中已经交代清楚了,而到这里我们又知道了 IBL 的方法,使用环境映射贴图来采样的到 入射辐照度函数 Li(p⃗)L_i(\vec{p})Li(p) ,而立体角 dω\mathrm{d} \omegadω 根据前面的教程中的方法也可以拆分为积分半球上关于天顶角 θ\thetaθ 和方位角 ϕ\phiϕ 的二重积分。所以编码已经不是问题了。只是对于物体表面上每个点来说,实际都需要成千上万次的计算,期间还夹杂着大量的采样操作,而且最终效果还不一定能达到令人接受的程度。显然这样的粗暴编码的方法,因为缺乏效率,就显得非常不“计算机科学”了。因此整个渲染方程就需要更进一步的解析和优化,直到整个过程的计算量能达到可接受的程度,或者说达到当前计算机硬件条件下可计算的程度。
3.2、 ksk_sks 项与菲涅尔项等价消除
首先在 DirectX12(D3D12)基础教程(十九)—— 多实例渲染 的第4节中,特意补充了之前被忽略的一个重要知识点,即渲染方程中有 “ ks=Fk_s = Fks=F ”, 所以最终正确的渲染方程表达式是:
Lo(p⃗,ωo⃗)=∫Ω(kdcπ+DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗L_o(\vec{p},\vec{\omega_o}) = \int\limits_{\Omega} (k_d \cfrac{c}{\pi} + \cfrac{ D F G }{ 4 (\vec{\omega_o} \cdot \vec{n} )(\vec{\omega_i} \cdot \vec{n})}) L_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} \mathrm{d} \vec{\omega_i} Lo(p,ωo)=Ω∫(kdπc+4(ωo⋅n)(ωi⋅n)DFG)Li(p,ωi)n⋅ωidωi
也即 DFG 部分中已经包含了 ksk_sks 项,所以不用再乘一遍。这本质上说明菲涅尔反射其实就是所谓的镜面反射的重要系数。只是镜面反射是关于光线的纯几何近似,而菲涅尔反射则是更加“物理”的近似,并且也更“真实”。所以一般在 PBR 中再说镜面反射和漫反射时基本就不再是传统光照模型中的纯几何化的含义了,这点大家一定要注意区分,不要简单的觉得 PBR 是故弄玄虚的将光照问题复杂化了。
本质上说 PBR 渲染已经跟传统光照模型没有任何关系了,二者区别极大。当然有一种说法认为传统光照模式是物理光照模型的一种极简近似,但这是针对真实的物理光照本身说的,而不是针对 PBR 说的。请注意这些说法中的本质含义和区别。

3.3、拆分“漫反射项”和“镜面反射项”
如果你有一点关于积分运算的知识的话,那么明显的就可以发现渲染方程可以进一步拆分为两个部分:
Lo(p⃗,ωo⃗)=∫Ω(κdcπ)Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗+∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗=κdcπ∫ΩLi(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗⏟漫反射项−Diffuse+∫Ω(DFG4(ωo⃗⋅n⃗)(ωi⃗⋅n⃗))Li(p⃗,ωi⃗)n⃗⋅ωi⃗dωi⃗⏟镜面反射项−Specular\mathrm{L}_{o}(\vec{p},\vec{\omega_{o}}) = \mathop{\int}_{\Omega} ( \kappa_d \frac{c}{\pi})\mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} d\vec{\omega_i} \quad \\[2ex] + \quad \mathop{\int}_{\Omega}( \frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} d\vec{\omega_i} \\[2ex] = \underbrace{ \kappa_d \frac{c}{\pi} \mathop{\int}_{\Omega} \mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} \mathrm{d} \vec{\omega_i} }_{漫反射项-Diffuse} \quad \\[2ex] + \quad \underbrace{ \mathop{\int}_{\Omega}( \frac{DFG}{4 ( \vec{\omega_o} \cdot \vec{n} ) (\vec{\omega_i} \cdot \vec{n} ) } ) \mathrm{L}_i(\vec{p},\vec{\omega_i}) \vec{n} \cdot \vec{\omega_i} d\vec{\omega_i} }_{镜面反射项-Specular} Lo(p,ωo)=∫Ω(κdπc)Li(p,ωi)n⋅ωidωi+∫Ω(4(ωo⋅n)(ωi⋅n)DFG)Li(p,ωi)n⋅ωidωi=漫反射项−Diffuseκdπc∫ΩLi(p,ωi)n⋅ωidωi+镜面反射项−Specular∫Ω(4(ωo⋅n)(ωi⋅n)DFG)Li(p,ωi)n⋅ωidωi
这样反射积分就变成了两个部分积分的和。这样显然是有好处的,因为这种形式两个积分项可以分开计算,最后再来求和,所以可以被方便的用来并行计算。
相关文章:

DirectX12(D3D12)基础教程(二十一)—— PBR:IBL 的数学原理(2/5)
目录3、IBL 数学原理3.1、基于微平面理论的 “Cook-Torrance” 模型回顾3.2、 ksk_sks 项与菲涅尔项等价消除3.3、拆分“漫反射项”和“镜面反射项”3、IBL 数学原理 接下来,就让我们正式进入整个 IBL 的数学原理的旅程。请注意,前方高能! …...

嵌入式学习笔记——SysTick(系统滴答)
系统滴答前言SysTick概述SysTick是个啥SysTick结构框图1. 时钟选择2.计数器部分3.中断部分工作一个计数周期(从重装载值减到0)的最大延时时间工作流程SysTick寄存器1.控制和状态寄存器SysTick->CTRL2.重装载值寄存器SysTick->LOAD3.当前值寄存器Sy…...

Linux实操之服务管理
文章目录一、服务(service)管理介绍:service管理指令查看服务名服务的运行级别(runlevel):CentOS7后运行级别说明chkconfig指令介绍一、服务(service)管理介绍: 服务(service)本质就是进程,但是是运行在后台的,通常都会监听某个端口,等待其它…...

基于Java+SpringBoot+vue的毕业生信息招聘平台设计和实现【源码+论文+演示视频+包运行成功】
博主介绍:专注于Java技术领域和毕业项目实战 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟 Java项目精品实战案例(200套) 目录 一、效果演示 二、…...
智能生活垃圾检测与分类系统(UI界面+YOLOv5+训练数据集)
摘要:智能生活垃圾检测与分类系统用于日常生活垃圾的智能监测与分类,通过图片、视频和摄像头识别生活垃圾,对常见的可降解、纸板、玻璃、金属、纸质和塑料等类别垃圾进行检测和计数,以协助垃圾环保分类处理。本文详细介绍基于YOLO…...

建立农村污水处理设施已经成为了当务之急!
在现代社会中,随着城市化进程的加速和人口的增长,选择农村污水处理设备进行污水处理已经成为了一个非常重要的问题。虽然城市中的污水处理设施得到了很好的发展,但是农村地区的污水处理还存在很多问题。 在农村地区,由于缺乏污水…...
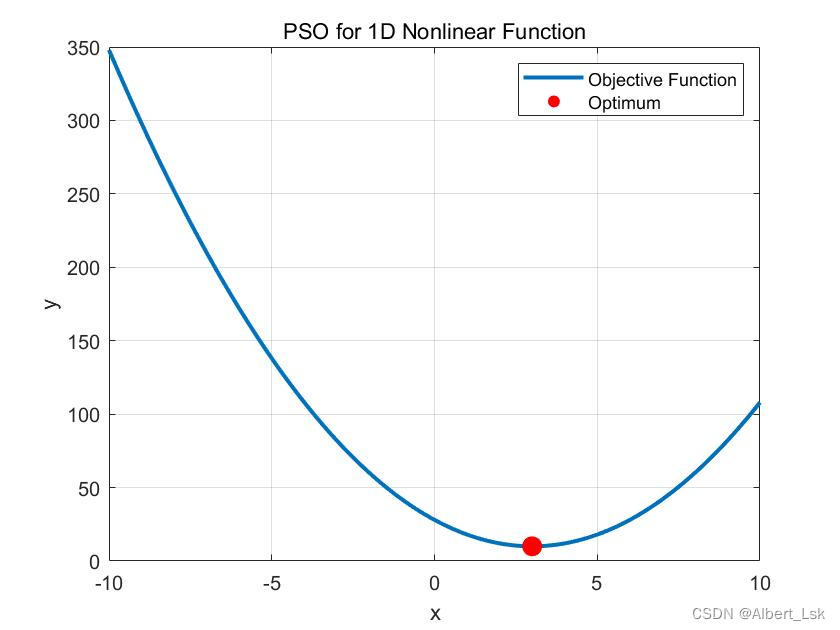
【Matlab算法】粒子群算法求解一维线性函数问题(附MATLAB代码)
MATLAB求解一维线性函数问题前言正文函数实现可视化处理可视化结果前言 一维线性函数,也称为一次函数,是指只有一个自变量xxx的函数,且函数表达式可以写成yaxbyaxbyaxb的形式,其中aaa和bbb是常数。具体来说,aaa称为斜…...

【JavaEE】Thread 类及常用方法
一、Thread 类Thread 类我们可以理解为是 java 用于管理线程的一个类,里面封装了操作系统提供的线程管理这一方面的 API (Thread 是优化后的结果), Java 代码创建的每一个线程,可以理解为为 Thread 实例化的对象,Threa…...

C语言数据结构初阶(7)----队列
CSDN的uu们,大家好。这里是C语言数据结构的第七讲。 目标:前路坎坷,披荆斩棘,扶摇直上。 博客主页:姬如祎队列的基础知识队列(queue)是只允许在一端进行插入操作,而在另一端进行删除…...

代码随想录二刷 day01 | 704. 二分查找 27. 移除元素 977. 有序数组的平方
代码随想录二刷day01704. 二分查找27. 移除元素977. 有序数组的平方704. 二分查找 题目链接 做这种题最好现在纸上写一写,如果在大脑中想,可能一会就晕了。 二刷的时候发现了一个新的知识点 即: >>的作用 二分法第二种写法:…...
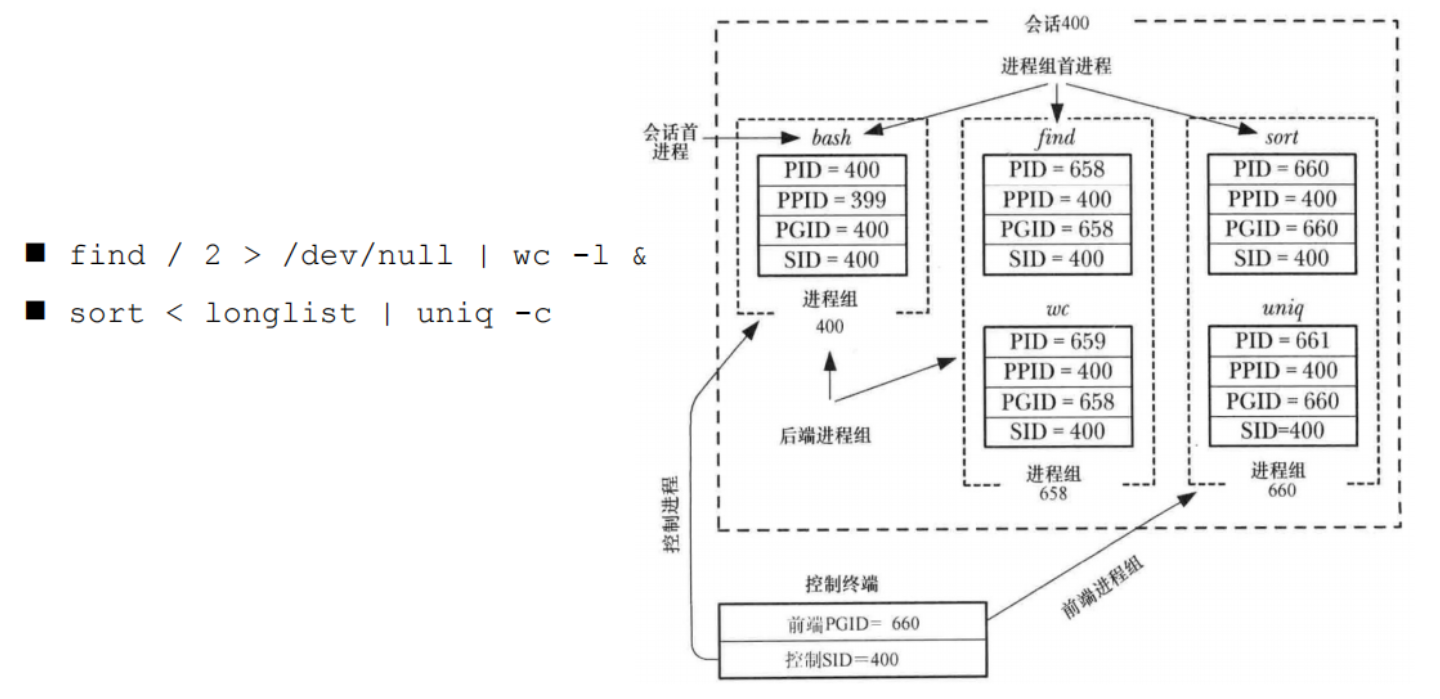
Linux 终端、进程组、会话、守护进程
文章目录一、终端概念终端概念控制终端二、进程组概念进程组概述进程组相关 API会话会话概念会话相关 API创建会话注意事项守护进程守护进程介绍守护进程模型守护进程参考代码守护进程相关 API参考文章一、终端概念 终端概念 1、终端(Terminal) 终端是…...

你是否有潜质成为谷歌开发者专家?加入 GDE 成长计划,释放潜力!
谷歌开发者专家 (Google Developer Experts,GDE),又称谷歌开发者专家项目,是由一群经验丰富的技术专家、具有社交影响力的开发者和思想领袖组成的全球性社区。通过在各项活动演讲以及各个平台上发布优质内容来积极助力开发者、企业和技术社区…...
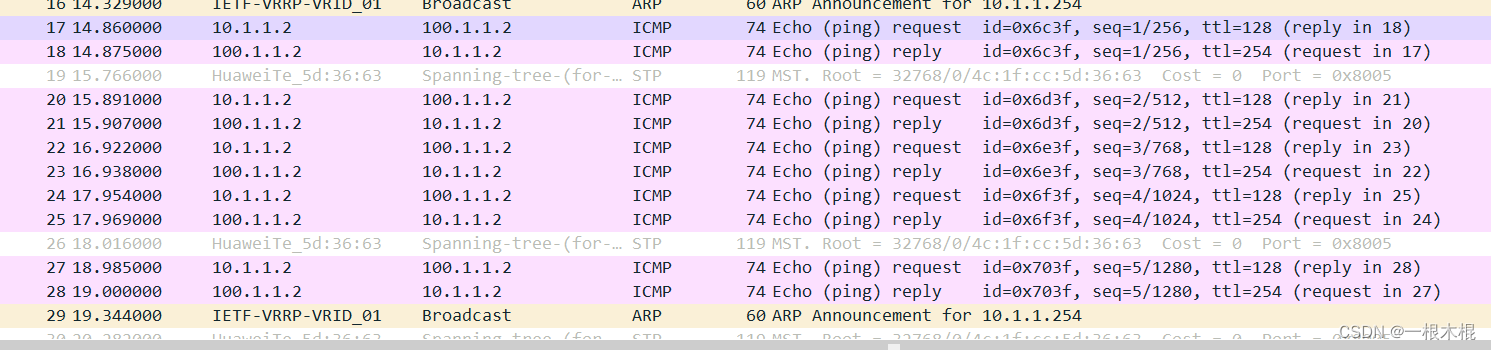
安全防御之防火墙篇(二)
目录 1.防火墙如何处理双通道协议? 2.防火墙如何处理NAT? 3.防火墙支持哪些NAT技术,主要应用的场景是什么? 4.当内网PC通过公网域名解析访问内网服务器的时候,会存在什么问题,如何解决?请详细…...

设计必备,5个png免抠素材网站,建议收藏
做设计、PPT都需要用到大量的免抠素材,职场中熟练使用Photoshop的人毕竟是少数,也很少有人愿意花费时间去精细抠图。那这5个免抠素材网站一定要收藏好,可以有效帮你节省时间,提高工作效率。 1、菜鸟图库 https://www.sucai999.co…...

shell 脚本expect
expect 是什么 expect - programmed dialogue with interactive programs(与互动程序进行程序对话) 定义脚本执行的 shell #!/usr/bin/expect -f 定义的是执行 expect 可执行文件的链接路径(或真实路径),功能类似于bas…...
第十九天 Maven总结
目录 Maven 1. 前言 2. 概述 2.1 介绍 2.2 安装 3. IDEA集成Maven 3.1 集成Maven环境 3.2 创建Maven项目 3.3 Maven坐标详解 3.4 导入maven项目 4. 依赖管理 4.1 依赖配置 4.2 依赖传递 4.3 依赖范围 4.4 生命周期 4.5 插件 Maven 1. 前言 1). 什么是Maven? …...

ESP8266-NodeMCU开发板-------开发板介绍(1)
目录 认识ESP8266-NodeMCU开发板编辑 GPIO编号与NodeMCU开发板引脚名的区别: ESP8266 GPIO编号与NodeMCU开发板引脚名的对应关系 可用引脚 电压电流限制 特殊引脚情况说明 上拉电阻/下拉电阻 模拟输入 通讯 认识ESP8266-NodeMCU开发板 初识NodeMCU开发板 (第1章-第…...
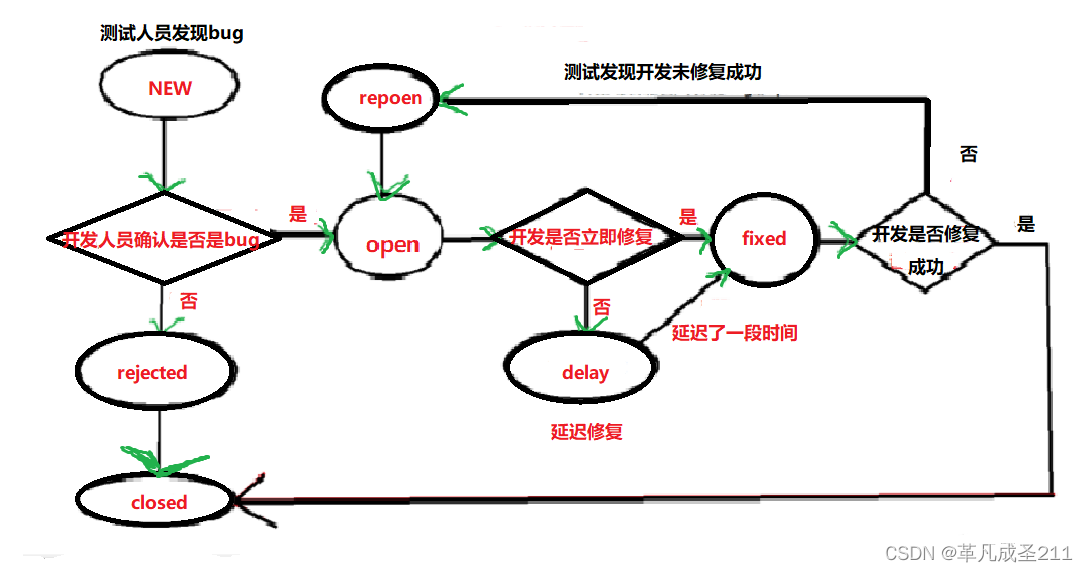
【测试开发篇3】软件测试的常用概念
目录 一、软件测试的生命周期(5个步骤) ①需求分析(两个角度) 用户角度: 开发人员的角度: ②测试计划 ③测试设计、测试开发 ④执行测试 ⑤测试评估 二、软件测试贯穿项目的整个生命周期的体现 需求分析阶段 计划阶段 设计阶段 编码阶段 …...

javaEE初阶 — JavaScript WebAPI
文章目录什么是 DOMDOM 树获取元素1. querySelector2. querySelectorAll事件1. 事件三要素2. 代码案例获取 / 修改元素内容1. innerHTML获取 / 修改元素属性获取 / 修改表单元素属性获取 / 修改样式属性1. 修改内联样式(修改 style 属性的值)2. 修改元素…...

UE实现地面动态交互效果
文章目录 1.实现目标2.实现过程2.1 SphereMask2.2 材质实现2.3 位置更新3.参考资料1.实现目标 基于SphereMask材质节点实现人物在地面一定范围内的颜色高亮效果。 2.实现过程 实现原理是首先通过,SphereMask材质节点更具计算输出Mask值,其中在球体半径内的输入1,在外部的则…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
