【Matlab算法】粒子群算法求解一维线性函数问题(附MATLAB代码)
MATLAB求解一维线性函数问题
- 前言
- 正文
- 函数实现
- 可视化处理
- 可视化结果
前言
一维线性函数,也称为一次函数,是指只有一个自变量xxx的函数,且函数表达式可以写成y=ax+by=ax+by=ax+b的形式,其中aaa和bbb是常数。具体来说,aaa称为斜率,决定了函数图像的倾斜程度;bbb称为截距,决定了函数图像与yyy轴的交点位置。
优化一维线性函数的目标是找到一个使得函数值最小或最大的xxx值。
粒子群算法(Particle Swarm Optimization,PSO) 是一种启发式优化算法,它源于对鸟群捕食行为的研究。在粒子群算法中,被优化的问题被视为一个多维空间中的目标函数,算法通过模拟群体中每个粒子在空间中的搜索行为来寻找目标函数的全局最优解。
每个粒子在搜索空间中的位置表示一个潜在解,其速度表示了搜索方向和步长。每个粒子具有一个适应度值,该适应度值根据目标函数的表现来计算。粒子群算法通过协同粒子的行为来优化目标函数。粒子的速度和位置在每个迭代中被更新,使其朝着群体中的最佳位置和全局最佳位置移动。
粒子群算法的运行过程如下:
- 初始化粒子群,包括每个粒子的初始位置和速度,并设置全局最佳位置和全局最佳适应度值为初始值。
- 计算每个粒子的适应度值,更新全局最佳位置和全局最佳适应度值。
- 更新每个粒子的速度和位置,根据每个粒子当前位置与全局最佳位置之间的差异来调整速度和位置。
- 重复步骤
2和3,直到达到指定的停止准则,如达到最大迭代次数或满足收敛要求。
在实践中,粒子群算法经常与其他优化算法结合使用,例如遗传算法、模拟退火等。这些算法的组合可以提高搜索效率和准确性,从而提高优化问题的解决效率。
正文
粒子群算法可以用来优化一维线性函数。具体地,我们可以将一维线性函数f(x)f(x)f(x)转化为目标函数y(x)y(x)y(x),使得y(x)y(x)y(x)的取值范围为[0, 1],且函数值越小表示越优,函数值越大表示越差。具体转化方式如下:
y(x)=f(x)−minf(x)maxf(x)−minf(x)y(x) = \frac{f(x) - \min f(x)}{\max f(x) - \min f(x)}y(x)=maxf(x)−minf(x)f(x)−minf(x)
其中maxf(x)\max f(x)maxf(x)和minf(x)\min f(x)minf(x)分别是函数f(x)f(x)f(x)在一定区间内的最大值和最小值。这样,优化f(x)f(x)f(x)就可以转化为优化y(x)y(x)y(x),即找到使得y(x)y(x)y(x)最小的xxx值。
在粒子群算法中,我们可以初始化一些粒子,并在每一次迭代中更新粒子的速度和位置,直到达到一定的停止条件。在更新速度和位置时,我们需要使用上文提到的公式,同时需要指定一些超参数,例如学习因子、惯性权重、加速度权重等。具体可以参考之前的回答。
在优化一维线性函数时,粒子群算法可以在一定的迭代次数内找到一个相对较优的解。但是需要注意,对于线性函数,我们也可以通过解析求导的方式直接求得最优解,因此粒子群算法在实际中并不常用于优化线性函数。
函数实现
%%
clear
close all
warning off
clc
%%
% 调用粒子群算法求解
x_min = -10;
x_max = 10;
n_pop = 50;
n_iter = 100;
w = 0.8;
c1 = 1.5;
c2 = 1.5;
[gbest, gbest_val] = pso(@objfun, x_min, x_max, n_pop, n_iter, w, c1, c2);% 输出结果
fprintf('最优解:x = %f,最优值:%f\n', gbest, gbest_val);% 目标函数
function y = objfun(x)y = 2*(x-3).^2 + 10;
end% 粒子群算法
function [gbest, gbest_val] = pso(objfun, x_min, x_max, n_pop, n_iter, w, c1, c2)% 参数设置x_range = x_max - x_min;v_min = -x_range;v_max = x_range;% 初始化粒子pop = x_min + rand(n_pop, 1) * x_range;v = v_min + rand(n_pop, 1) * (v_max - v_min);pbest = pop;pbest_val = objfun(pop);[gbest_val, gbest_idx] = min(pbest_val);gbest = pbest(gbest_idx);% 迭代for i = 1:n_iter% 更新速度和位置r1 = rand(n_pop, 1);r2 = rand(n_pop, 1);v = w*v + c1*r1.*(pbest-pop) + c2*r2.*(gbest-pop);pop = pop + v;% 边界处理pop(pop < x_min) = x_min;pop(pop > x_max) = x_max;% 更新个体历史最优和全局历史最优pbest_val_new = objfun(pop);pbest_update_idx = pbest_val_new < pbest_val;pbest(pbest_update_idx) = pop(pbest_update_idx);pbest_val(pbest_update_idx) = pbest_val_new(pbest_update_idx);[gbest_val_new, gbest_idx_new] = min(pbest_val);if gbest_val_new < gbest_valgbest = pbest(gbest_idx_new);gbest_val = gbest_val_new;endend
end
通过改变xxx的范围xmin=−10;xmax=10;x_min = -10;x_max = 10;xmin=−10;xmax=10;来得到一维线性函数的最优值
可视化处理
%%
clear
close all
warning off
clc
%%
% 调用粒子群算法求解
x_min = -10;
x_max = 10;
n_pop = 50;
n_iter = 100;
w = 0.8;
c1 = 1.5;
c2 = 1.5;
[gbest, gbest_val] = pso(@objfun, x_min, x_max, n_pop, n_iter, w, c1, c2);% 输出结果
fprintf('最优解:x = %f,最优值:%f\n', gbest, gbest_val);% 可视化处理
x = linspace(x_min, x_max, 1000);
y = objfun(x);
figure();
plot(x, y, 'linewidth', 2);
hold on;
scatter(gbest, gbest_val, 100, 'r', 'filled');
xlabel('x');
ylabel('y');
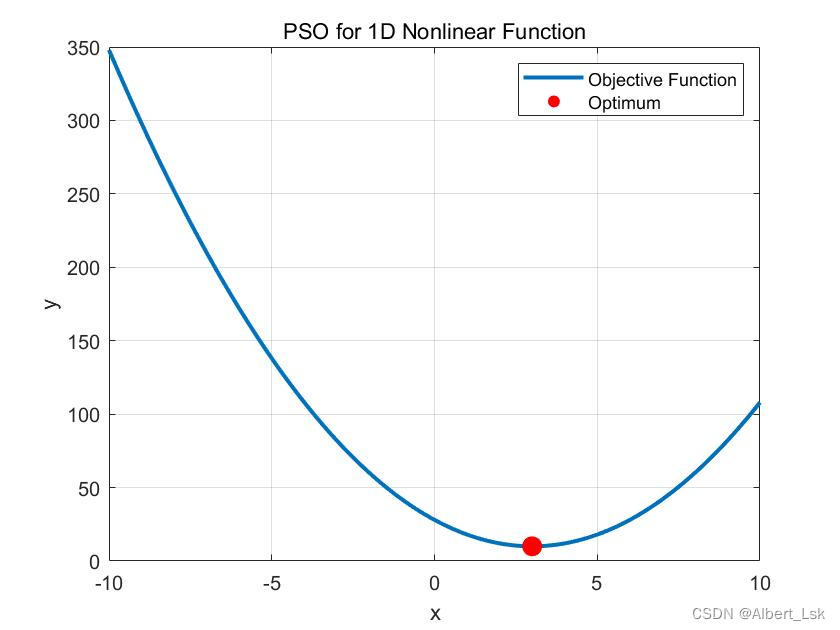
title('PSO for 1D Nonlinear Function');
legend('Objective Function', 'Optimum');
grid on;% 目标函数
function y = objfun(x)y = 2*(x-3).^2 + 10;
end% 粒子群算法
function [gbest, gbest_val] = pso(objfun, x_min, x_max, n_pop, n_iter, w, c1, c2)% 参数设置x_range = x_max - x_min;v_min = -x_range;v_max = x_range;% 初始化粒子pop = x_min + rand(n_pop, 1) * x_range;v = v_min + rand(n_pop, 1) * (v_max - v_min);pbest = pop;pbest_val = objfun(pop);[gbest_val, gbest_idx] = min(pbest_val);gbest = pbest(gbest_idx);% 迭代for i = 1:n_iter% 更新速度和位置r1 = rand(n_pop, 1);r2 = rand(n_pop, 1);v = w*v + c1*r1.*(pbest-pop) + c2*r2.*(gbest-pop);pop = pop + v;% 边界处理pop(pop < x_min) = x_min;pop(pop > x_max) = x_max;% 更新个体历史最优和全局历史最优pbest_val_new = objfun(pop);pbest_update_idx = pbest_val_new < pbest_val;pbest(pbest_update_idx) = pop(pbest_update_idx);pbest_val(pbest_update_idx) = pbest_val_new(pbest_update_idx);[gbest_val_new, gbest_idx_new] = min(pbest_val);if gbest_val_new < gbest_valgbest = pbest(gbest_idx_new);gbest_val = gbest_val_new;endend
end
可视化结果
相关文章:

【Matlab算法】粒子群算法求解一维线性函数问题(附MATLAB代码)
MATLAB求解一维线性函数问题前言正文函数实现可视化处理可视化结果前言 一维线性函数,也称为一次函数,是指只有一个自变量xxx的函数,且函数表达式可以写成yaxbyaxbyaxb的形式,其中aaa和bbb是常数。具体来说,aaa称为斜…...

【JavaEE】Thread 类及常用方法
一、Thread 类Thread 类我们可以理解为是 java 用于管理线程的一个类,里面封装了操作系统提供的线程管理这一方面的 API (Thread 是优化后的结果), Java 代码创建的每一个线程,可以理解为为 Thread 实例化的对象,Threa…...

C语言数据结构初阶(7)----队列
CSDN的uu们,大家好。这里是C语言数据结构的第七讲。 目标:前路坎坷,披荆斩棘,扶摇直上。 博客主页:姬如祎队列的基础知识队列(queue)是只允许在一端进行插入操作,而在另一端进行删除…...

代码随想录二刷 day01 | 704. 二分查找 27. 移除元素 977. 有序数组的平方
代码随想录二刷day01704. 二分查找27. 移除元素977. 有序数组的平方704. 二分查找 题目链接 做这种题最好现在纸上写一写,如果在大脑中想,可能一会就晕了。 二刷的时候发现了一个新的知识点 即: >>的作用 二分法第二种写法:…...
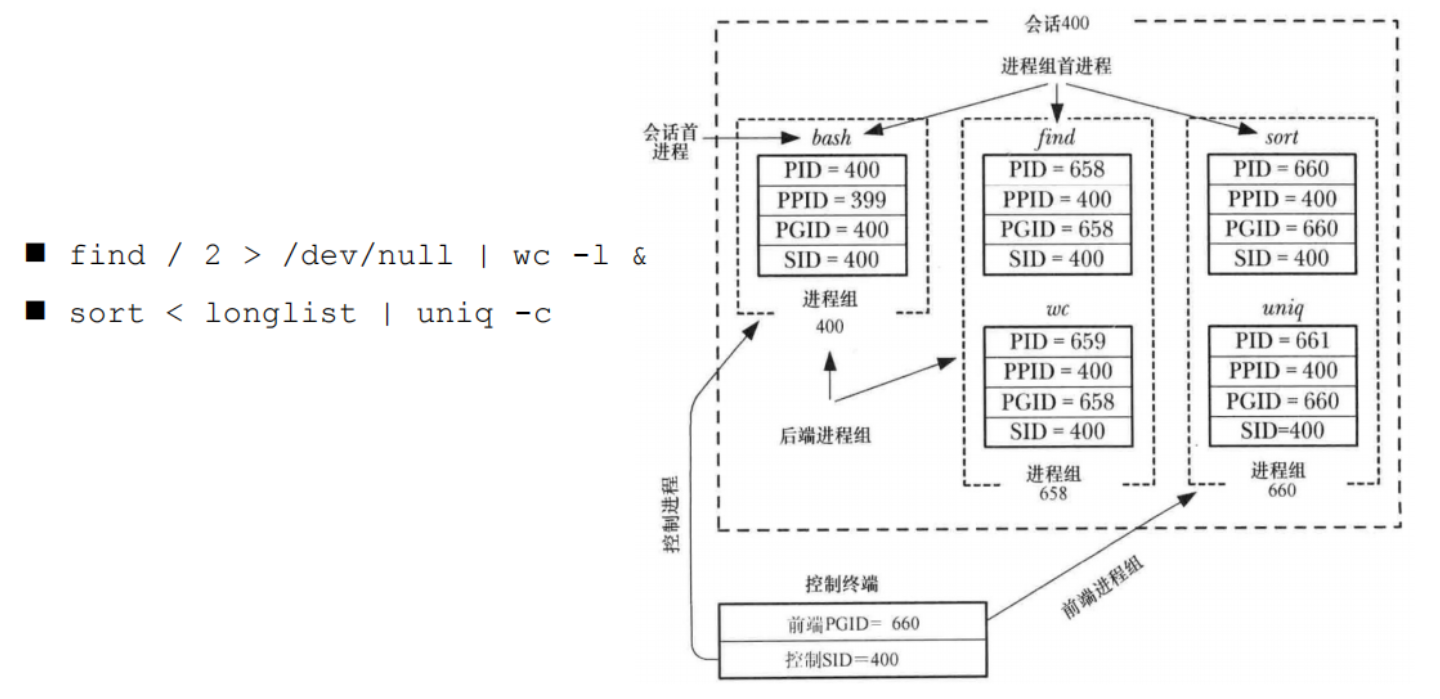
Linux 终端、进程组、会话、守护进程
文章目录一、终端概念终端概念控制终端二、进程组概念进程组概述进程组相关 API会话会话概念会话相关 API创建会话注意事项守护进程守护进程介绍守护进程模型守护进程参考代码守护进程相关 API参考文章一、终端概念 终端概念 1、终端(Terminal) 终端是…...

你是否有潜质成为谷歌开发者专家?加入 GDE 成长计划,释放潜力!
谷歌开发者专家 (Google Developer Experts,GDE),又称谷歌开发者专家项目,是由一群经验丰富的技术专家、具有社交影响力的开发者和思想领袖组成的全球性社区。通过在各项活动演讲以及各个平台上发布优质内容来积极助力开发者、企业和技术社区…...
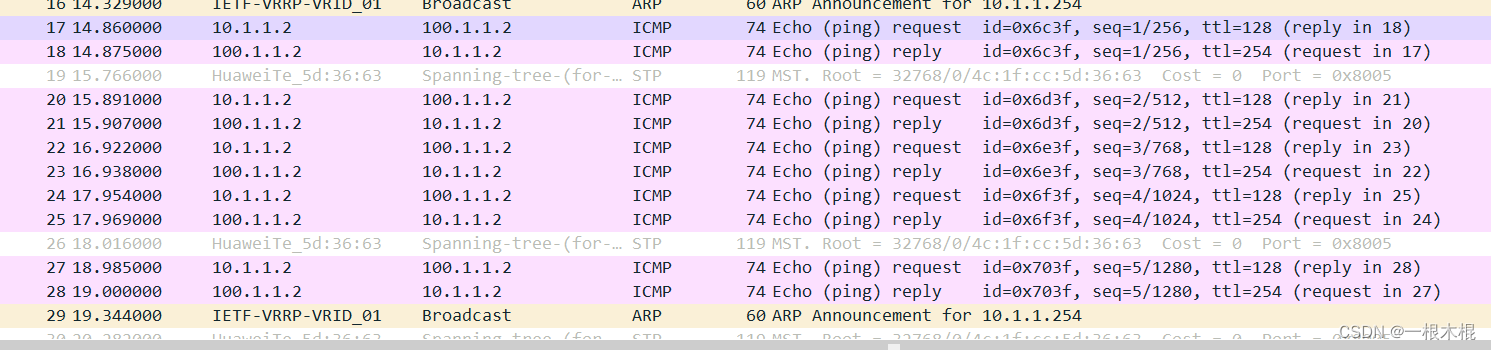
安全防御之防火墙篇(二)
目录 1.防火墙如何处理双通道协议? 2.防火墙如何处理NAT? 3.防火墙支持哪些NAT技术,主要应用的场景是什么? 4.当内网PC通过公网域名解析访问内网服务器的时候,会存在什么问题,如何解决?请详细…...

设计必备,5个png免抠素材网站,建议收藏
做设计、PPT都需要用到大量的免抠素材,职场中熟练使用Photoshop的人毕竟是少数,也很少有人愿意花费时间去精细抠图。那这5个免抠素材网站一定要收藏好,可以有效帮你节省时间,提高工作效率。 1、菜鸟图库 https://www.sucai999.co…...

shell 脚本expect
expect 是什么 expect - programmed dialogue with interactive programs(与互动程序进行程序对话) 定义脚本执行的 shell #!/usr/bin/expect -f 定义的是执行 expect 可执行文件的链接路径(或真实路径),功能类似于bas…...
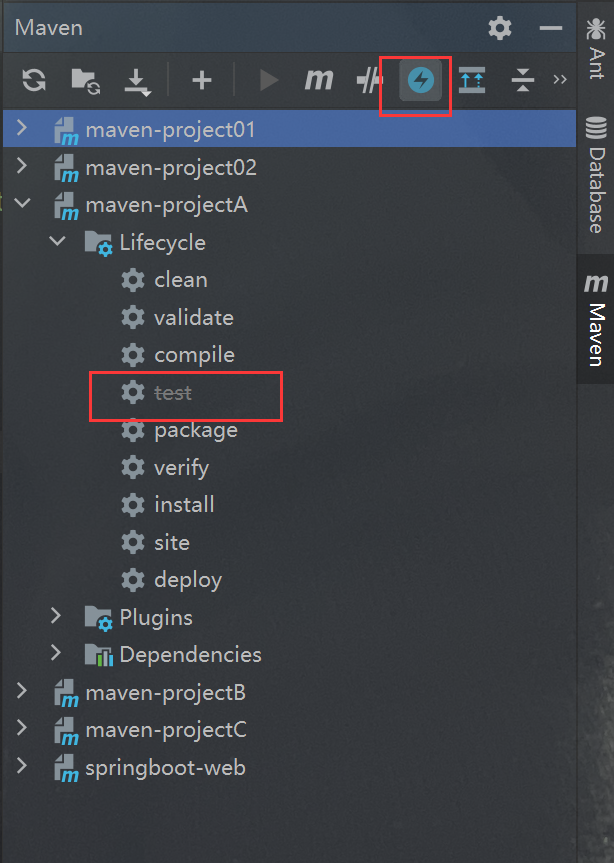
第十九天 Maven总结
目录 Maven 1. 前言 2. 概述 2.1 介绍 2.2 安装 3. IDEA集成Maven 3.1 集成Maven环境 3.2 创建Maven项目 3.3 Maven坐标详解 3.4 导入maven项目 4. 依赖管理 4.1 依赖配置 4.2 依赖传递 4.3 依赖范围 4.4 生命周期 4.5 插件 Maven 1. 前言 1). 什么是Maven? …...

ESP8266-NodeMCU开发板-------开发板介绍(1)
目录 认识ESP8266-NodeMCU开发板编辑 GPIO编号与NodeMCU开发板引脚名的区别: ESP8266 GPIO编号与NodeMCU开发板引脚名的对应关系 可用引脚 电压电流限制 特殊引脚情况说明 上拉电阻/下拉电阻 模拟输入 通讯 认识ESP8266-NodeMCU开发板 初识NodeMCU开发板 (第1章-第…...
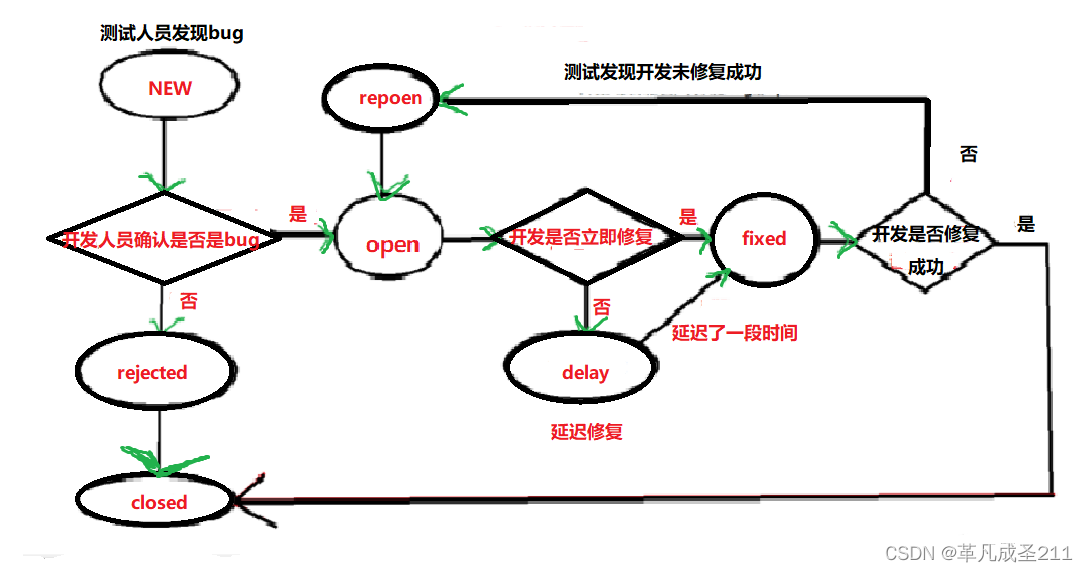
【测试开发篇3】软件测试的常用概念
目录 一、软件测试的生命周期(5个步骤) ①需求分析(两个角度) 用户角度: 开发人员的角度: ②测试计划 ③测试设计、测试开发 ④执行测试 ⑤测试评估 二、软件测试贯穿项目的整个生命周期的体现 需求分析阶段 计划阶段 设计阶段 编码阶段 …...

javaEE初阶 — JavaScript WebAPI
文章目录什么是 DOMDOM 树获取元素1. querySelector2. querySelectorAll事件1. 事件三要素2. 代码案例获取 / 修改元素内容1. innerHTML获取 / 修改元素属性获取 / 修改表单元素属性获取 / 修改样式属性1. 修改内联样式(修改 style 属性的值)2. 修改元素…...

UE实现地面动态交互效果
文章目录 1.实现目标2.实现过程2.1 SphereMask2.2 材质实现2.3 位置更新3.参考资料1.实现目标 基于SphereMask材质节点实现人物在地面一定范围内的颜色高亮效果。 2.实现过程 实现原理是首先通过,SphereMask材质节点更具计算输出Mask值,其中在球体半径内的输入1,在外部的则…...
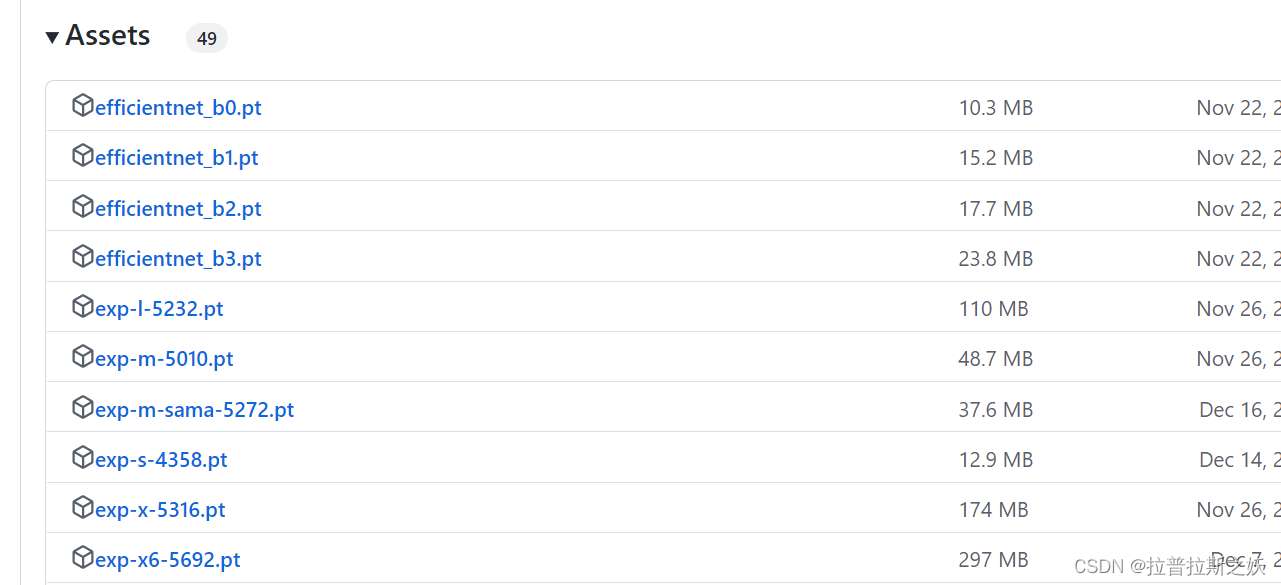
如何用自己的数据训练YOLOv5
如何训练YOLOv5 1. Clone the YOLOv5 repository and install dependencies: git clone https://github.com/ultralytics/yolov5.git cd yolov5 pip install -r requirements.txt2. 整理数据,使其适配YOLO训练 Step1:Organize your dataset in the fo…...

【基础算法】数组相关题目
系列综述: 💞目的:本系列是个人整理为了秋招算法的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于代码随想录进行的,每个算法代码参考leetcode高赞回答和…...

MatBox—基于PyQt快速入门matplotlib的教程库
MatBox—基于PyQt快速入门matplotlib的教程库 __ __ _ _ _ _ _ _ _______ _ _ _ | \/ | | | | | | | | |(_)| | |__ __| | | (_) | || \ / | __ _ |…...

go channel使用
go语言中有一句名言: 不要通过共享内存来通信,而应该通过通信来共享内存。 channel实现了协程间的互相通信。 目录 一、channel声明 二、向channel发送数据 三、从channel读取数据 1. i, ok : <-c 2. for i : range c(常用)…...
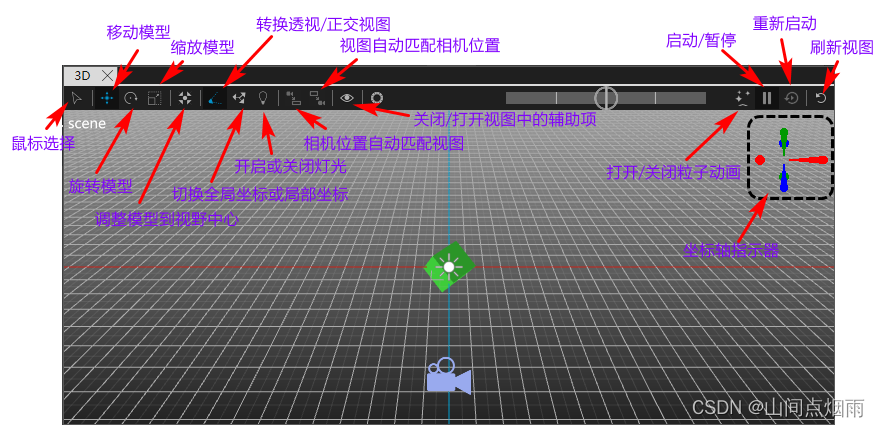
5. QtDesignStudio中的3D场景
1. 说明: 三维渲染开发是Design Studio的重要功能,且操作方便,设计效率非常高,主要用到的控件是 View3D ,可以在3D窗口中用鼠标对模型直接进行旋转/移动/缩放等操作,也可以为模型设置各种动画,执行一系列的…...

人工智能的几个研究方向
人工智能主要研究内容是:分布式人工智能与多智能主体系统、人工思维模型、知识系统、知识发现与数据挖掘、遗传与演化计算、人工生命、人工智能应用等等。 其中热门研究有以下几种。 一、计算机视觉 就包括图像识别,视频识别,具体应用有人…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
