Gitlab中access token 和Deploy token的区别
在GitLab中,Access Token和Deploy Token是两种不同类型的令牌,用于不同的目的。以下是它们的主要区别:
### Access Token
1. **用途**:
- 用于用户身份验证,允许用户以编程方式访问GitLab API。
- 可以用于克隆、推送代码,管理项目和组,执行CI/CD任务等。
2. **类型**:
- **Personal Access Token**:与用户账户关联,具有用户账户的权限。
- **Project Access Token**:与特定项目关联,具有项目级别的权限。
3. **权限**:
- 可以配置不同的权限范围(Scopes),如`api`、`read_user`、`read_repository`、`write_repository`等。
4. **创建方式**:
- 个人访问令牌:用户可以在GitLab的“User Settings”中的“Access Tokens”部分创建。
- 项目访问令牌:项目Maintainer或Owner可以在项目的“Settings”中的“Access Tokens”部分创建。
### Deploy Token
1. **用途**:
- 专门用于CI/CD和自动化部署,允许只读或读写访问项目的仓库和包注册表。
- 适用于需要在CI/CD管道中访问仓库的场景。
2. **类型**:
- 仅与特定项目关联。
3. **权限**:
- 可以配置为只读(read_repository)或读写(write_repository)。
- 还可以配置对包注册表的访问权限(read_registry、write_registry)。
4. **创建方式**:
- 项目Maintainer或Owner可以在项目的“Settings”中的“Repository”部分创建。
### 示例
假设你有一个GitLab仓库URL `https://gitlab.example.com/username/repo.git`,以下是如何使用这两种令牌的示例:
#### 使用Access Token
```sh
git clone https://<access_token>@gitlab.example.com/username/repo.git
```
#### 使用Deploy Token
假设Deploy Token的用户名是 `deploy_user`,令牌是 `deploy_token`:
```sh
git
clone https://deploy_user:deploy_token@gitlab.example.com/username/repo.git
```
### 总结
- **Access Token**:用于用户身份验证,具有广泛的权限范围,适用于各种操作。
- **Deploy Token**:专门用于CI/CD和自动化部署,权限较为有限,适用于特定场景。
选择使用哪种令牌取决于你的具体需求和安全策略。
相关文章:

Gitlab中access token 和Deploy token的区别
在GitLab中,Access Token和Deploy Token是两种不同类型的令牌,用于不同的目的。以下是它们的主要区别: ### Access Token 1. **用途**: - 用于用户身份验证,允许用户以编程方式访问GitLab API。 - 可以用于克隆…...
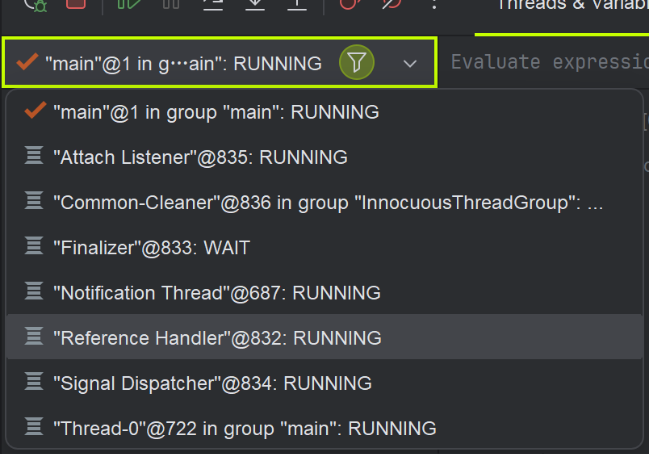
【多线程】线程的五种创建方法
文章目录 线程在 Java 代码中编写多线程程序Thread 标准库 创建线程的写法1 . 继承 Thread 类代码回调函数休眠操作:sleep()抢占式执行观察线程jconsoleIDEA 内置调试器 2 . 实现 Runnable 接口代码 3. 匿名内部类创建 Thread ⼦类对象代码匿名内部类 4.匿名内部类创…...

关闭窗口工具类 - C#小函数类推荐
此文记录的是一个关于关闭窗口工具类。 /***关闭窗口工具类Austin Liu 刘恒辉Project Manager and Software DesignerE-Mail: lzhdim163.comBlog: http://lzhdim.cnblogs.comDate: 2024-01-15 15:18:00使用方法:CloseWindowUtil.CloseWindow(this.Handle);***/n…...

Xilinx FPGA 原语解析(一):IBUFDS_GTE3 差分时钟输入缓冲器
目录 1.使用说明 2.实例化代码 3.参数解释 4.端口连接 1.使用说明 IBUFDS_GTE3 是Xilinx FPGA 中用于高速接口的差分时钟信号输入缓冲器。 BUFDS_GTEx,x2/3/4(不同系列的FPGA x的值不同),其中UltraScale使IBUFDS_GTE3…...

力扣SQL50 患某种疾病的患者 正则表达式
Problem: 1527. 患某种疾病的患者 在SQL查询中,REGEXP 是用于执行正则表达式匹配的操作符。正则表达式允许使用特殊字符和模式来匹配字符串中的特定文本。具体到你的查询,^DIAB1|\\sDIAB1 是一个正则表达式,它使用了一些特殊的通配符和符号。…...

k8s集群的资源发布方式(滚动/蓝绿/灰度发布)及声明式管理方法
目录 1.常见的发布方式 2.滚动发布 3.蓝绿发布 4.实现金丝雀发布(Canary Release) 5.声明式管理方法 1.常见的发布方式 蓝绿发布:两套环境交替升级,旧版本保留一定时间便于回滚优点:用户无感知,部署和回滚速度较…...

SwiftUI 中掌握 ScrollView 的使用:滚动可见性
文章目录 前言视图修饰符应用场景可见性完整示例ContentViewVideoPlayerViewScrollViewVisibilityApp 总结 前言 我们的滚动 API 中又有一个重要的新增功能:滚动可见性。现在,你可以获取可见标识符列表,或者快速检查并监控 ScrollView 内视图…...

中药养发护发
按照中医理论,头发和肝肾有密切联系,肝主血,肾藏精, 其华在发,肝肾强健,上荣于头,则毛发乌黑浓密. 中药育发的应用 以当归,天麻,桑疹子养血润发,配合干姜祛风活血,能通畅经络, 加快循环,激活毛囊,能促进皮肤组织营养成分吸收和废弃物的排泄,改善 头发生态. 用苦参 皂角 清热化…...
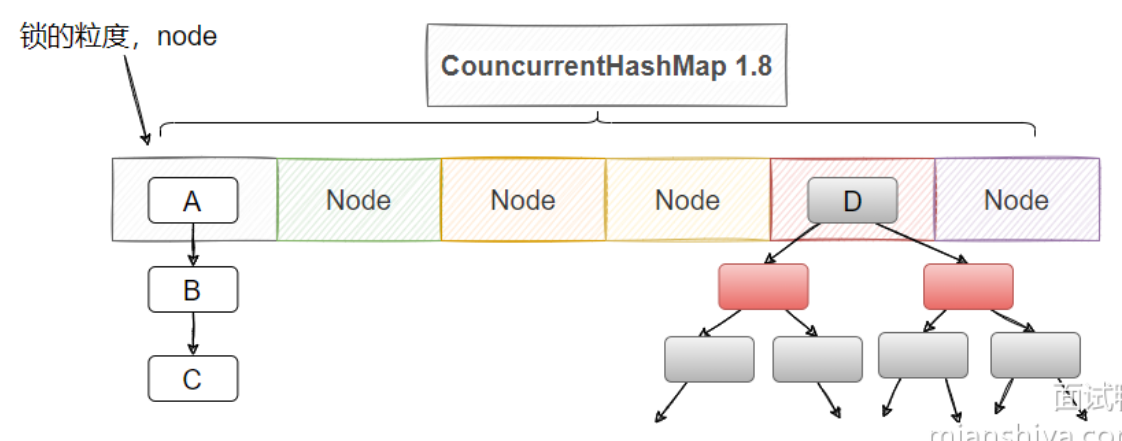
Java面试题-集合类
目录 1、请简单介绍下 Java 的集合类吧。 Collection Set TreeSet和HashSet List ArrayList 和 LinkedList 数组和链表的区别 Java 的列表有哪些实现类? Vector Queue Map 能说下 HashMap 的实现原理吗? 能说下 HashMap 的扩容机制吗&#x…...

【Vue3】组件通信之v-model
【Vue3】组件通信之v-model 背景简介开发环境开发步骤及源码总结 背景 随着年龄的增长,很多曾经烂熟于心的技术原理已被岁月摩擦得愈发模糊起来,技术出身的人总是很难放下一些执念,遂将这些知识整理成文,以纪念曾经努力学习奋斗的…...
)
【Golang 面试 - 进阶题】每日 3 题(二)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...

Java中等题-多数元素2(力扣)【摩尔投票升级版】
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。 示例 1: 输入:nums [3,2,3] 输出:[3] 示例 2: 输入:nums [1] 输出:[1]示例 3: 输入:num…...

100条超牛的DOS命令
目录 1. 文件和目录管理 1.1 列出文件和目录 1.1.1 dir 1.1.2 dir /w 1.2 切换目录 1.2.1 cd 1.2.2 cd .. 1.3 创建和删除目录 1.3.1 md / mkdir 1.3.2 rd / rmdir 1.4 文件操作 1.4.1 del / erase 1.4.2 copy 1.5 文件重命名 1.5.1 ren / rename 1.5.2 move …...

大数据信用报告查询会不会留下查询记录?怎么选择查询平台?
最近有不少网友都在咨询一个问题,那就是大数据信用报告查询会不会留下查询记录,会不会对自己的征信产生影响,下面本文就详细为大家介绍一下,希望对你了解大数据信用有帮助。 首先、大数据信用与人行征信是独立的 很多人只知道人行…...

JS【详解】内存泄漏(含泄漏场景、避免方案、检测方法),垃圾回收 GC (含引用计数、标记清除、标记整理、分代式垃圾回收)
内存泄漏 在执行一个长期运行的应用程序时,应用程序分配的内存没有被释放,导致可用内存逐渐减少,最终可能导致浏览器崩溃或者应用性能严重下降的情况,即 JS 内存泄漏 可能导致内存泄漏的场景 不断创建全局变量未及时清理的闭包&…...

第三期书生大模型实战营之Llamaindex RAG实践
基础任务 任务要求:基于 LlamaIndex 构建自己的 RAG 知识库,寻找一个问题 A 在使用 LlamaIndex 之前InternLM2-Chat-1.8B模型不会回答,借助 LlamaIndex 后 InternLM2-Chat-1.8B 模型具备回答 A 的能力,截图保存。 streamlit界面…...

【从0到1进阶Redis】Jedis 理解事务
笔记内容来自B站博主《遇见狂神说》:Redis视频链接 小伙伴们可以熟悉一下本专栏的 Redis 文章,可以更好地理解 正常操作 package oldfe.study;import com.alibaba.fastjson.JSONObject; import redis.clients.jedis.Jedis; import redis.clients.jedis.T…...

MySQL之Lost connection to MySQL server during query复现测试
测试Lost connection to MySQL server during query复现条件 环境报错信息复现测试方式一方式二 环境 Python: 3.8/3.9 Mysql: 5.x 报错信息 File "/Users/xxx/lib/python3.9/site-packages/sqlalchemy/dialects/mysql/base.py", line 2509, in do_rollbackdbapi_con…...

中国AI大模型场景探索及产业应用调研报告
AI大模型发展态势 定义 AI大模型是指在机器学习和深度学习领域中,采用大规模参数(至少在一亿个以上)的神经网络模型,AI大模型在训练过程中需要使用大量的算力和高质量的数据资源。 产业规模 2023年,中国大模型市场规模为147亿。结合《202…...

Linux--shell脚本语言—/—<1>
一、shell简介 Shell是一种程序设计语言。作为命令语言,它交互式解释和执行用户输入的命令或者自动地解释和执行预先设定好的一连串的命令;作为程序设计语言,它定义了各种变量和参数,并提供了许多在高级语言中才具有的控制结构&am…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
