C#中投影运算的深入解析与实例应用
文章目录
- 1、投影运算的基本语法
- 2、投影运算的高级用法
- 3、投影运算在向量空间中的运用
- 4、投影运算在数据库和XML中的实际应用
- 5、投影运算能用于哪些实际场景?
- 6、结论

在C#编程中,投影运算是一种常用的数据操作技术,它可以将一个数据集合转换成新的格式或结构。投影运算在LINQ(语言集成查询)中扮演着重要的角色,使得C#开发者能够更加灵活地对数据进行处理和转换。本文将详细介绍C#中的投影运算,包括基本概念、语法以及在向量空间、数据库和XML中的应用。
1、投影运算的基本语法
在C#中,投影运算通常使用LINQ的.Select()方法来实现。.Select()方法接受一个lambda表达式作为参数,该表达式定义了从原始数据集合到新数据集合的转换逻辑。关键字“Projection”用于表示这个转换过程。
示例:
假设我们有一个简单的学生类 Student,包含姓名和年龄属性,我们希望从学生列表中选择所有学生的姓名。
using System;
using System.Collections.Generic;
using System.Linq;class Program
{static void Main(){List<Student> students = new List<Student>{new Student { Name = "Alice", Age = 20 },new Student { Name = "Bob", Age = 21 },new Student { Name = "Charlie", Age = 19 }};// 使用 LINQ 进行投影选择学生的姓名var studentNames = from student in studentsselect student.Name;foreach (var name in studentNames){Console.WriteLine(name);}}
}class Student
{public string Name { get; set; }public int Age { get; set; }
}
解析:
- 在这个示例中,我们使用 LINQ 查询语法从 students 列表中选择所有学生的姓名。
- select student.Name 表示我们选择每个学生对象的 Name 属性作为投影结果。
- 最终,通过 foreach 循环输出了每个学生的姓名。
2、投影运算的高级用法
投影运算不仅可以用来创建包含所需属性的新类型,还可以用来进行更复杂的转换。例如,我们可以使用.Select()来过滤数据、连接多个数据源、或者应用更复杂的转换逻辑。
以下是一个使用.Select()进行连接操作的例子:
// 假设有一个学生列表和一个课程列表
List<Student> students = new List<Student>
{// ... 学生数据
};
List<Course> courses = new List<Course>
{// ... 课程数据
};// 使用LINQ进行连接操作
var enrolledStudents = students.SelectMany(s => s.Grades.Select(g => new { Student = s, Course = g })).GroupBy(g => g.Course).Select(g => new{CourseName = g.Key,StudentsCount = g.Count()});// 输出每个课程的名称和学生数量
foreach (var course in enrolledStudents)
{Console.WriteLine($"课程名称:{course.CourseName}, 学生数量:{course.StudentsCount}");
}
在这个例子中,我们首先使用.SelectMany()来连接学生和他们的成绩,然后使用.GroupBy()来按课程分组,最后使用.Select()来投影出我们感兴趣的课程名称和学生数量。
3、投影运算在向量空间中的运用
在向量空间中,投影运算用于将一个向量投影到另一个向量上。这可以通过计算两个向量的点积来实现。以下是一个投影运算在向量空间中的示例:
using System;public class Vector
{public double[] Coordinates { get; set; }public Vector(double[] coordinates){Coordinates = coordinates;}public static Vector Projection(Vector v1, Vector v2){double dotProduct = v1.Coordinates.Aggregate(0.0, (current, coordinate) => current + coordinate * v2.Coordinates[Array.IndexOf(v2.Coordinates, coordinate)]);double magnitudeSquared = v2.Coordinates.Aggregate(0.0, (current, coordinate) => current + coordinate * coordinate);double scalar = dotProduct / magnitudeSquared;return new Vector(v2.Coordinates.Select(coordinate => coordinate * scalar).ToArray());}
}public class Program
{public static void Main(){// 创建两个向量Vector v1 = new Vector(new double[] { 1, 2, 3 });Vector v2 = new Vector(new double[] { 2, 1, 1 });// 计算投影向量Vector projection = Vector.Projection(v1, v2);// 输出结果Console.WriteLine($"投影向量:{string.Join(", ", projection.Coordinates)}");}
}
在这个例子中,我们定义了一个Vector类,用于表示向量及其坐标。Projection方法接受两个向量作为参数,并计算第一个向量在第二个向量上的投影。
4、投影运算在数据库和XML中的实际应用
在数据库和XML中,投影运算可以用于查询和转换数据。以下是一个在数据库中使用投影运算的示例:
using System;
using System.Data.SqlClient;public class Program
{public static void Main(){// 连接数据库using (SqlConnection connection = new SqlConnection("YourConnectionString")){connection.Open();// 执行SQL查询并投影结果var projectedOrders = connection.Query<dynamic>("SELECT OrderID, CustomerID, OrderDate FROM Orders").Select(order => new { order.OrderID, CustomerName = order.CustomerID.ToString(), order.OrderDate });// 输出结果foreach (var order in projectedOrders){Console.WriteLine($"订单号:{order.OrderID}, 客户名称:{order.CustomerName}, 订单日期:{order.OrderDate}");}}}
}
在这个例子中,我们使用LINQ to SQL的方法来执行数据库查询,并使用.Select()方法来投影结果。我们创建了一个新的匿名类型,它包含了订单ID、客户名称和订单日期。
在XML中,投影运算可以用于从XML文档中提取特定元素或属性。以下是一个使用LINQ to XML进行投影运算的示例:
using System;
using System.Xml.Linq;public class Program
{public static void Main(){// 创建XML文档XDocument doc = XDocument.Load("yourfile.xml");// 投影运算:选择所有的书籍元素var books = from book in doc.Descendants("book")select new{Title = book.Element("title").Value,Author = book.Element("author").Value};// 输出结果foreach (var book in books){Console.WriteLine($"书名:{book.Title}, 作者:{book.Author}");}}
}
在这个例子中,我们使用LINQ to XML来加载XML文档,并使用.Select()方法来投影文档中的book元素。我们创建了一个新的匿名类型,它包含了书名和作者属性。
5、投影运算能用于哪些实际场景?
投影运算在实际开发场景中有广泛的应用,以下是一些常见的使用场景:
- 数据筛选和展示: 在用户界面中,往往需要根据用户的需求显示特定格式的数据。例如,在一个电子商务应用中,可以将商品列表投影为只包含产品名称、价格和图片的列表。
- 数据转换: 在需要将数据从一种格式转换为另一种格式时,投影运算非常有用。例如,将一组客户对象的列表转换为包含客户姓名和联系方式的列表。
- 数据聚合: 在分析数据时,经常需要对数据进行聚合,如计算销售数据的总额、平均值、最大值和最小值等。LINQ的.Select()和.GroupBy()可以结合使用来实现这些操作。
- 关系操作: 在处理关系型数据时,投影可以用于实现关系的投影,即将多个表的数据合并并转换为新的结构,以满足业务需求。例如,从订单、客户和产品三个表中投影出所有订单及其对应的客户和产品信息。
- 管道操作: 在数据处理的管道中,投影运算可以用于中间步骤,用来转换数据以便于后续的处理。例如,在处理日志文件时,可能需要先投影出感兴趣的事件类型和相关信息,然后再进行过滤或分析。
- API返回数据格式化: 在设计和实现API时,投影运算可以用来根据不同的客户端需求返回不同格式的数据。例如,一个API可能需要根据请求头的不同,返回JSON或XML格式的数据。
- 数据迁移: 在将数据从一个系统迁移到另一个系统时,可能需要将数据投影为新的数据模型以适应新系统的结构。
- 测试数据生成: 在测试阶段,可能需要生成特定格式的数据来满足测试需求,投影运算可以帮助生成这些特定格式的数据。
在所有这些场景中,投影运算都能帮助开发者以声明式的方式表达数据转换逻辑,从而使得代码更加简洁、可读性强,并且易于维护。
6、结论
C#中的投影运算是一种强大的数据操作技术,它可以帮助开发者以声明式的方式转换和查询数据。通过LINQ的.Select()方法,我们可以轻松实现数据集合到新结构或格式的转换。无论是在向量空间、数据库还是XML中,投影运算都有广泛的应用场景。通过掌握投影运算的基本概念和语法,读者可以提升自己在C#编程中的实际操作能力,编写出更加简洁、高效的数据处理代码。
相关文章:

C#中投影运算的深入解析与实例应用
文章目录 1、投影运算的基本语法2、投影运算的高级用法3、投影运算在向量空间中的运用4、投影运算在数据库和XML中的实际应用5、投影运算能用于哪些实际场景?6、结论 在C#编程中,投影运算是一种常用的数据操作技术,它可以将一个数据集合转换成…...

HTML+CSS練習---空隙產生記錄
1.第一層和第二層之間的間隙:以為導航欄超過高度朝下擠下來了 2.第2層兩個div中的空隙 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Document</title><style>font-face {f…...

【leetcode】相同的树、另一棵树的子树、翻转二叉树(利用深度优先遍历)
Hi~!这里是奋斗的明志,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 🌱🌱个人主页:奋斗的明志 🌱🌱所属专栏:数据结构、LeetCode专栏 📚本系…...

Linux系统窗口水印难点分析
给应用程序加水印是保护数据的一种方式,window上可以通过给进程通过注入的方法给进程的窗口创建一个同大小的副窗口,在副窗口上绘制水印内容,同时设置副窗口透明同时透传事件,这样就可以达到在源窗口上显示水印的效果且不影响程序…...
LabVIEW与CANopen实现自动化生产线的设备控制与数据采集
在某工厂的自动化生产线上,多个设备通过CANopen网络进行通信和控制。这些设备包括传感器、执行器和PLC,它们共同负责监测和控制生产过程中的关键参数,如温度、压力、速度等。为了实现对整个生产线的集中监控和管理,工厂决定使用La…...
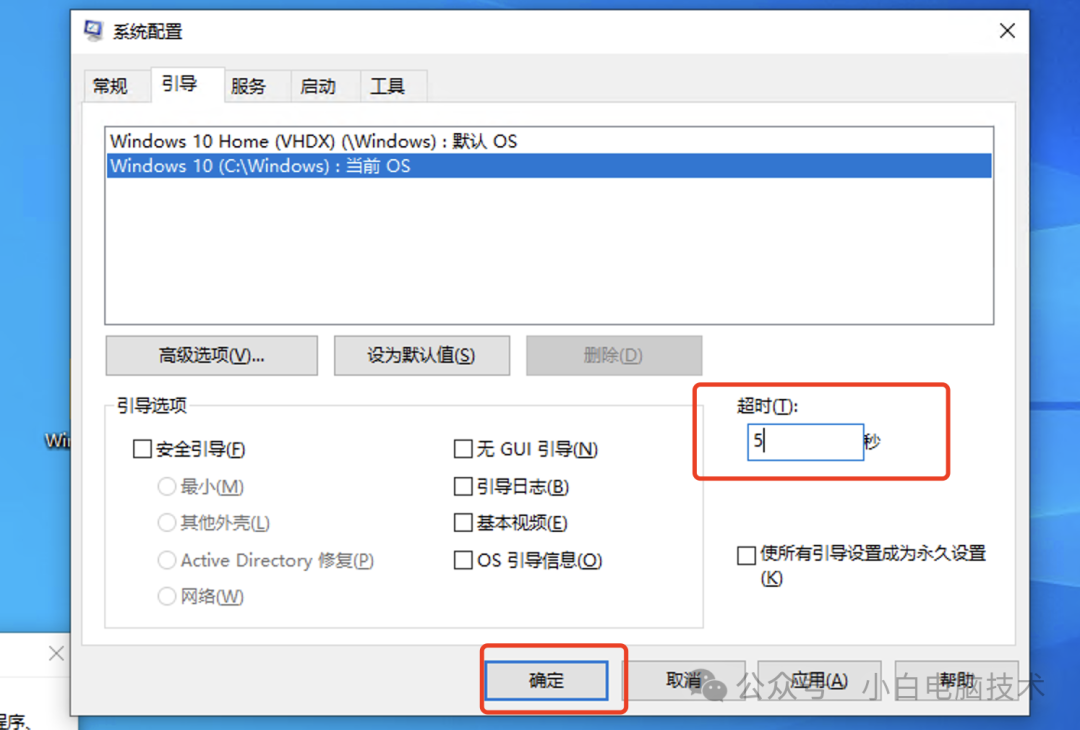
吃惊!这个Windows双系统方法逆天了|UEFI篇
前言 最近小白在折腾别的系统教程,偶然间发现居然有一个很nice的Windows双系统教程。于是于是,果断尝试了一下,发现真的很可行! 这个双系统的办法并不需要使用到WinPE系统,因此并不需要使用到U盘,只需要在…...

【C语言基础】C语言试题复习
1. 执行下面的程序段后,k 的值是_______。 int k1,n325; do { k*n%10;n/10;}while(n); 解析: 给定 n 325 和初始 k 1,代码中的循环将会进行如下操作: 第一次循环:n % 10 得到 5,因此 k * 5,即 k 1 * 5 …...

一拖三无线充底座-带给你极致的便利生活
随着科技的不断进步,无线充电技术已经逐渐渗透到我们日常生活的方方面面,一拖三无线充底座作为其中的佼佼者,以其高效、便捷的特点受到广大用户的青睐。本文将从电磁感应原理、多线圈设计、频率匹配、电能传输、功率分配以及充电管理六个方面…...

探索 Electron:打造深度书籍挖掘机的搜索体验
Electron是一个开源的桌面应用程序开发框架,它允许开发者使用Web技术(如 HTML、CSS 和 JavaScript)构建跨平台的桌面应用程序,它的出现极大地简化了桌面应用程序的开发流程,让更多的开发者能够利用已有的 Web 开发技能…...

tomato靶场
扫描网址端口 访问一下8888 我们用kali扫描一下目录 访问这个目录 产看iofo.php源码,发现里面有文件包含漏洞 访问/etc/passwd/发现确实有文件包含漏洞 远程连接2211端口 利用报错,向日志文件注入木马,利用文件包含漏洞访问日志文件 http:/…...

【Vue】computed计算对象不生效问题?
问题描述 最近使用vuex来管理全局状态,遇到了computed计算state中数据却不生效的问题。 原因分析: 先看vue官网示例: computed接收的是一个getter函数,但是这个getter函数是懒加载并且有缓存的,当计算属性最终计算…...

算法小白的进阶之路(力扣9~12)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 非常期待和您一起在这个小…...

DOCKER容器中安装JDK1. 8 详细步骤
1.通过查找JDK8的远程镜像 docker search jdk 2.选择一个远程镜像下载到本地仓库 #拉取镜像 docker pull kdvolder/jdk8#查看镜像 docker images 可以看到REPOSITORY列下面出现了kdvolder/jdk8 3.在docker容器中运行jdk8的镜像 docker run -di --namejdk1.8 kdvolder/jdk…...

计算机毕业设计Python+Tensorflow股票推荐系统 股票预测系统 股票可视化 股票数据分析 量化交易系统 股票爬虫 股票K线图 大数据毕业设计 AI
1、用pycharm打开项目,一定要打开包含manage.py文件所在文件夹 2、配置解释器:建议使用Anaconda(Python 3.8(base)),低于3.8版本的,页面会不兼容 3、安装依赖库:打开pycharm的终端,输入: pip in…...
)
深度学习常见的卷积和注意力机制文章集锦(持续更新)
卷积 友好链接1 卷积原理:几种常用的卷积(标准卷积、深度卷积、组卷积、扩展卷积、反卷积) 友好链接2 一文看尽深度学习中的20种卷积(附源码整理和论文解读) 友好链接3 深度学习中组卷积(Group convolution)、深度卷积…...

如何在立创EDA的PCB电路板导入logo图案
1、首先制作好logo图案,一般为公司logo图标,如下图 2、打开立创EDA的PCB文件,如下图 3、将PCB的图层切换到丝印层: 4、然后选择EDA菜单栏的放置---图片: 5、进入后点击选择图片,将logo图片导入,…...

springboot集成canal
目录 一、打开mysql的binlog1.1 打开 MySQL 配置文件 my.cnf(通常位于 /etc/mysql/my.cnf 或 /etc/my.cnf)并添加或修改以下设置:1.2 重启mysql服务1.3 验证是否生效 二、 部署canal 服务端(docker)2.1 下载启动脚本(可…...
)
leetcode数论(2447. 最大公因数等于 K 的子数组数目)
前言 经过前期的数据结构和算法学习,开始以OD机考题作为练习题,继续加强下熟练程度。 描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 nums 的子数组中元素的最大公因数等于 k 的子数组数目。 子数组 是数组中一个连续的非空序列…...

实现数组扁平化的几种方式
目标: 实现数组扁平化[1,[2,[3,4,5]]] > [1,2,3,4,5] 我们有几种方法可以实现,分别为: 1、递归 function flatten(list){return list.reduce((tar, cur) > {if(Array.isArray(cur)){tar tar.concat(flatten(cur));} else {tar.push(cur);}return tar;}, []); } flatt…...

3D打印技术正悄然重塑模具工业格局
虽被誉为“工业之母”的模具在批量生产中仍占据核心地位,但3D打印以其“无模”直接成型的特性,在小批量、非标准化及复杂结构件制造领域展现出独特优势,随着技术和装备的不断发展,目前3D打印正逐渐向批量生产渗透,某品…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
