深入理解Python中的列表推导式
深入理解Python中的列表推导式
在Python编程中,列表推导式(List Comprehension)是一种简洁而强大的语法,用于创建和操作列表。它不仅提高了代码的可读性,还能显著减少代码的行数。本文将详细介绍什么是列表推导式,如何使用它,以及一些实际应用示例,帮助读者更好地理解和运用这一特性。
一、什么是列表推导式?
列表推导式是一种用于生成列表的简洁方法。它允许我们通过一个表达式和一个可迭代对象(如列表、元组、字符串等)来创建新的列表。列表推导式的基本语法如下:
new_list = [expression for item in iterable if condition]
- expression:用于生成新列表中每个元素的表达式。
- item:可迭代对象中的每个元素。
- iterable:可以是列表、元组、字符串等可迭代对象。
- condition(可选):用于过滤元素的条件。
相关文章:

深入理解Python中的列表推导式
深入理解Python中的列表推导式 在Python编程中,列表推导式(List Comprehension)是一种简洁而强大的语法,用于创建和操作列表。它不仅提高了代码的可读性,还能显著减少代码的行数。本文将详细介绍什么是列表推导式,如何使用它,以及一些实际应用示例,帮助读者更好地理解…...

Android 实现左侧导航栏:NavigationView是什么?NavigationView和Navigation搭配使用
目录 1)左侧导航栏效果图 2)NavigationView是什么? 3)NavigationView和Navigation搭配使用 4)NavigationView的其他方法 一、实现左侧导航栏 由于Android这边没有直接提供左侧导航栏的控件,所以我尝试了…...

如何快速下载拼多多图片信息,效率高
图片是电商吸引顾客的关键因素,高质量的商品图片能提升产品吸引力,增强用户购买欲望。良好的视觉展示有助于建立品牌形象,提高转化率。同时,图片也是商品信息的主要传递媒介,对消费者决策过程至关重要。 使用图快下载器…...

windows 10下,修改ubuntu的密码
(1)在搜索框里面输入cmd,然后点击右键,选择管理员打开 Microsoft Windows [版本 10.0.22631.3880] (c) Microsoft Corporation。保留所有权利。 C:\Windows\System32>C: C:\Windows\System32>cd ../../ C:\>cd Users\ASUS\AppData\Local\Micros…...

【MySQL】慢sql优化全流程解析
定位慢sql 工具排查慢sql 调试工具:Arthas运维工具:Skywalking 通过以上工具可以看到哪个接口比较慢,并且可以分析SQL具体的执行时间,定位到哪个sql出了问题。 启用慢查询日志 慢查询日志记录了所有执行时间超过指定参数(lon…...

RabbitMQ高级特性 - 消息分发(限流、负载均衡)
文章目录 RabbitMQ 消息分发概述如何实现消费分发机制(限制每个队列消息数量)使用场景限流背景实现 demo 非公平发送(负载均衡)背景实现 demo RabbitMQ 消息分发 概述 RabbitMQ 的队列在有多个消费者订阅时,默认会通过…...
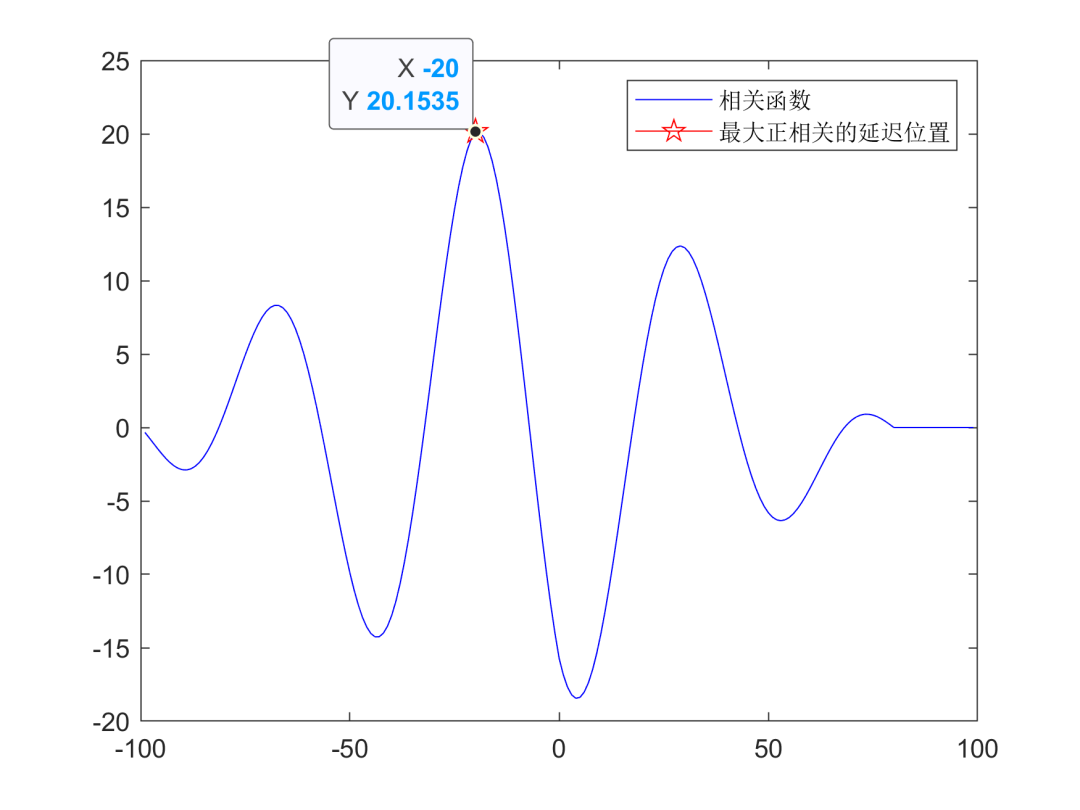
信号处理——自相关和互相关分析
1.概括 在信号处理中,自相关和互相关是相关分析非常重要的概念,它们能分析一个信号或两个信号在时间维度的相似性,在振动测试分析、雷达测距和声发射探伤得到了广泛的应用。自相关分析的研究对象为一个信号,互相关分析的研究对象…...
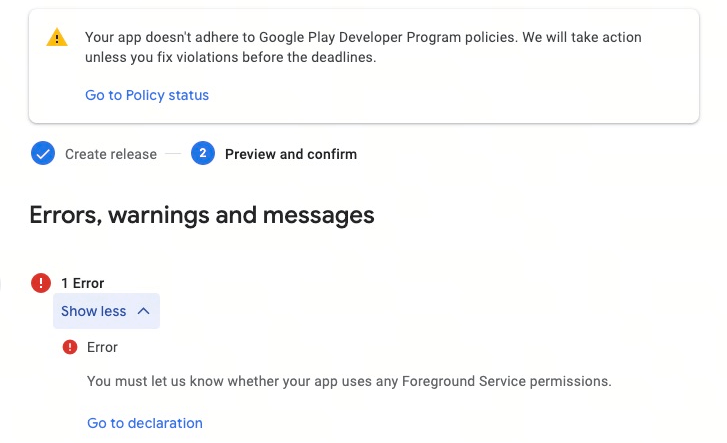
如何解决部分设备分辨率不适配
1)如何解决部分设备分辨率不适配 2)Unity中如何实现草的LOD 3)使用了Play Asset Delivery提交版本被Google报错 4)如何计算弧线弹道的落地位置 这是第396篇UWA技术知识分享的推送,精选了UWA社区的热门话题,…...

C#插件 调用存储过程(输出参数类型)
存储过程 CREATE PROCEDURE [dbo].[GetSum]num1 INT,num2 INT,result INT OUTPUT AS BEGINselect result num1 num2 END C#代码 using Kingdee.BOS; using Kingdee.BOS.App.Data; using Kingdee.BOS.Core.Bill.PlugIn; using Kingdee.BOS.Util; using System; using System.…...

代码随想录算法训练营day32 | 509. 斐波那契数 、70. 爬楼梯 、746. 使用最小花费爬楼梯
碎碎念:开始动态规划了!加油! 参考:代码随想录 动态规划理论基础 动态规划常见类型: 动规基础类题目背包问题打家劫舍股票问题子序列问题 解决动态规划问题应该要思考清楚的: 动态规划五部曲࿱…...

【人工智能专栏】Learning Rate Decay 学习率衰减
Learning Rate Decay 学习率衰减 使用格式 optimizer = torch.optim.SGD(model.paraters(), lr=0.1, momentum=0.9, weight_decay=1e-4) scheduler = torch.optim...
》题目集)
浙大版《C语言程序设计(第3版)》题目集
练习4-11 统计素数并求和 本题要求统计给定整数M和N区间内素数的个数并对它们求和。 输入格式: 输入在一行中给出两个正整数M和N(1≤M≤N≤500)。 输出格式: 在一行中顺序输出M和N区间内素数的个数以及它们的和,数字间以空格分隔。 输入…...

【学习笔记】Day 2
一、进度概述 1、inversionnet_train_light 试运行——未成功 2、DL-FWI基础入门培训-1,2,以及作业1的完成——暂未完成作业 二、详情 1、inversionnet_train_light 试运行 在补充完相关依赖后,运行仍有报错 产生原因:这个代码在当…...

Java中的Map(如果想知道Java中有关Map的知识点,那么只看这一篇就足够了!)
前言:在Java编程语言中,集合框架(Collection Framework)提供了一系列用于存储和操作数据的接口和类。其中,Map和Set是两个非常重要的接口,分别用于存储键值对和无重复元素的集合。 ✨✨✨这里是秋刀鱼不做梦…...

裸金属服务器详解
在云计算飞速发展的今天,裸金属服务器(Bare Metal Server, BMS)作为一种兼具传统物理服务器性能和虚拟化服务优势的计算资源,正逐渐成为企业和个人用户的重要选择。今天我们就来了解下关于裸金属服务器的定义、核心特点以及其在各…...

等待唤醒机制两种实现方法-阻塞队列
桌子上有面条-》吃货执行 桌子上没面条-》生产者制造执行 1、消费者等待 消费者先抢到CPU执行权,发现桌子上没有面条,于是变成等待wait状态,并释放CPU执行权,此时的CPU肯定会被厨师抢到,初始开始做面条,…...

数组项相加和 – 如何将 JavaScript 数组中的数字相加
JavaScript 中的数组是一个对象,它允许您在单个变量名称下存储多个值的有序集合,并以多种方式操作这些值。 在本文中,您将学习如何使用几种不同的方法计算给定数组中所有数字的总和。 具体来说,使用以下方法得到数组中所有数字的总…...
C#和S7-1200PLC S7.NET通信
1、一步步建立一个C#项目 一步步建立一个C#项目(连续读取S7-1200PLC数据)_s7协议批量读取-CSDN博客文章浏览阅读1.7k次,点赞2次,收藏4次。这篇博客作为C#的基础系列,和大家分享如何一步步建立一个C#项目完成对S7-1200PLC数据的连续读取。首先创建一个窗体应用。_s7协议批量…...

常用命令git branch
Git Branch 命令总结 列出分支 git branch:显示本地分支,当前分支会被标记。git branch -r:显示远程分支。git branch -a:显示所有本地和远程分支。 创建分支 git branch <branch_name>:创建一个新分支但不自…...

Android 制作系统签名
一、切换目录 cd build/target/product/security二、执行命令 1)将使用.pk8生成platform.priv.pem (.pem即可,文件名可随意修改)openssl pkcs8 -in platform.pk8 -inform DER -outform PEM -out platform.pem -nocrypt2)生成.p12,此时需输入两次密码,并且要记住 -name后所设置…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
