苹果 Safari 的隐私保护与广告追踪问题 :技术进展与挑战
隐私保护的进展与挑战
近年来,浏览器行业在隐私保护技术方面取得了显著进展,尤其是在广告追踪领域。谷歌的 Chrome 浏览器推广了隐私沙盒,通过将用户可能感兴趣的主题分类并推送给广告商。Mozilla Firefox 和 Meta Facebook 则推出了一种名为“隐私保护归因”的技术,目前在 Firefox 中默认启用,允许广告衡量功能,从而收集用户数据。

Safari 浏览器的新变化
苹果一直以注重隐私保护而闻名,许多用户也因此对苹果产品倍感放心。然而,Safari 浏览器最近的更新却让不少用户感到担忧。苹果的 WebKit 项目组在博文中详细介绍了 Safari 隐身模式下的隐私保护措施,并透露他们扩展了 Web AdAttributionKit。这项技术帮助广告网络在隐身模式下了解其营销活动的效果,与 Mozilla Firefox 的隐私保护归因技术类似,都会收集用户部分数据并与广告网络共享。
尽管苹果试图通过这些措施来解释其隐私保护承诺,但在隐身模式下增加广告追踪技术的决定无疑引发了用户的担忧。隐身模式本应是用户避免被追踪的最后一道防线,然而这一功能的加入使得隐身模式的实际效果大打折扣。
用户隐私与广告追踪的平衡
浏览器的隐身模式实际上并不能让用户完全隐身。广告商仍然可以通过用户的 IP 和设备信息来进行追踪。尽管个性化广告的投放可能受限,但基于 IP 地址的个性化广告依然可能投放。隐身模式唯一有效的保护措施是当用户关闭选项卡时,浏览器会自动清理浏览记录和 Cookies 等信息,但广告网络已经收集的信息仍会被保留。
提升隐私保护的建议
面对隐身模式下依然存在的广告追踪问题,用户可以采取一些措施来提升隐私保护:
- 使用隐私保护更强的浏览器:除了 Safari,用户还可以选择使用隐私保护措施更完善的浏览器,如 Brave 或 Tor 浏览器。
- 安装广告拦截插件:使用 uBlock Origin 等广告拦截插件,可以有效阻止广告网络的追踪。
- 使用 VPN:通过 VPN 隐藏 IP 地址,进一步保护上网隐私。
- 定期清理浏览数据:手动清理 Cookies、缓存等浏览数据,减少被追踪的可能性。
专业分析:Web AdAttributionKit的隐私影响
技术背景
Web AdAttributionKit 是苹果推出的一项用于广告归因的工具,旨在帮助广告商在不依赖第三方 Cookies 的情况下评估广告效果。这项技术的推出符合当前行业内减少第三方追踪的趋势,例如谷歌的隐私沙盒和 Mozilla 的隐私保护归因技术。然而,不同于这些技术,Web AdAttributionKit 在隐身模式下的运作方式引起了广泛关注。
隐私问题
隐身模式通常被用户视为一种保护隐私、避免追踪的手段。然而,Web AdAttributionKit 在隐身模式下的运作打破了这一常规。尽管苹果声称该技术仅限于广告效果评估,并不会收集用户个人识别信息,但其实际操作仍然涉及到一些隐私数据的处理和共享。
- 数据收集与共享:Web AdAttributionKit 会在用户点击广告后,收集特定数据用于评估广告效果。这些数据尽管被去标识化,但仍会与广告网络、网站和应用程序开发商共享。这种数据收集和共享的过程,使得用户在隐身模式下的浏览行为仍然可能被广告商追踪。
- 隐私保护机制的有效性:苹果在其隐私政策中提到,Web AdAttributionKit 采用了诸如频率上限、去标识化处理等隐私保护措施。然而,这些措施能否完全防止用户数据被滥用,仍然有待进一步观察。尤其是在隐身模式下,这些数据收集行为是否符合用户对隐私保护的期望,是一个值得深思的问题。
行业影响
苹果此举可能引发其他浏览器厂商的跟进或抵制。隐私保护与广告收入之间的平衡,一直是浏览器厂商面临的巨大挑战。随着用户对隐私保护需求的提升,如何在保障用户隐私的同时,为广告商提供有效的广告评估工具,成为一个亟需解决的难题。
结语
隐私保护与广告追踪之间的平衡一直是一个难题。尽管苹果在隐私保护方面做出了不少努力,但在隐身模式下引入广告追踪技术的决定无疑让不少用户感到不安。希望未来的浏览器技术能够在保护用户隐私的同时,找到更加合理的广告投放方式,为用户提供更安全、更私密的上网体验。
相关文章:

苹果 Safari 的隐私保护与广告追踪问题 :技术进展与挑战
隐私保护的进展与挑战 近年来,浏览器行业在隐私保护技术方面取得了显著进展,尤其是在广告追踪领域。谷歌的 Chrome 浏览器推广了隐私沙盒,通过将用户可能感兴趣的主题分类并推送给广告商。Mozilla Firefox 和 Meta Facebook 则推出了一种名为…...

pytest之fixture
Pytest 中 Fixture 的 yield 用法 在软件测试中,设置和清理测试环境是一个重要的环节。Pytest 作为一个功能强大的测试框架,通过 Fixture 机制简化了这一过程。特别是yield语句的使用,使得 Fixture 能够在测试前进行设置,并在测试…...

Rancher
文章目录 Rancher1. 安装和配置2. 服务部署和管理3. 容器自动化缩容和扩容 Rancher Rancher 是一个开源的企业级容器管理平台,旨在简化容器化应用的部署、管理和运维。它支持多种容器编排引擎,如 Kubernetes、Docker Swarm 等,并提供了统一的…...

Wordpress建站问题记录
从一月到七月因为工作的情况没有进行太深入的开发,想着整理一下把做一个独立站把博客多个渠道发布一下,遇到几个问题在这里记录一下. 先写一下我的配置 系统: centos7 php: 7.4 wordpress: 6.6.1 mysql:8.0.6 1. HTTP 500 Internal 这个问题出现在我将wordpress的文件夹全部…...

JavaFx中通过线程池运行或者停止多个周期性任务
在JavaFX中,要实现点击按钮启动多个周期性任务并通过多线程执行,并在任务结束后将结果写入多个文本组件中,同时提供另一个按钮来停止这些任务,你可以使用ScheduledExecutorService来管理周期性任务,并使用AtomicBoolea…...

使用RabbitMQ实现异步支付状态通知
在支付系统中,如何确保支付状态的准确传递和处理显得尤为重要。今天,我们将以一个支付流程为例,探讨在引入RabbitMQ前后的实现和优化。 改造前 在引入RabbitMQ之前,我们通常会直接在支付方法中完成所有的操作。这包括查询支付单…...

[最短路dijkstra],启动!!!
总时间复杂度为 O ( ( n m ) log m ) P4779 【模板】单源最短路径(标准版) #include<bits/stdc.h> #define ll long long #define fi first #define se second #define pb push_back #define PII pair<int,int > #define I…...

Java企业微信服务商代开发获取AccessToken示例
这里主要针对的是企业微信服务商代开发模式 文档地址 可以看到里面大致有三种token,一个是服务商的token,一个是企业授权token,还有一个是应用的token 这里面主要有下面几个参数 首先是服务商的 corpid 和 provider_secret ,这个可…...

How does age change how you learn?(2)年龄如何影响学习能力?(二)
Do different people experience decline differently? 不同人经历的认知衰退会有不同吗? Do all people experience cognitive decline uniformly?Or do some people’s minds slip while others stay sharp much longer? 所有人经历的认知衰退都是一样的吗?还是有些人…...

可验证随机函数 vrf 概述
一、什么是VRF 背景: 在传统的区块链中,常用的随机算法是基于伪随机数生成器(Pseudorandom Number Generator,PRNG)的。PRNG是一种确定性算法,它根据一个初始种子生成一个看似随机的序列。在区块链中,通常使用的是伪随机数序列来选择区块的创建者、确定验证节点的轮换…...

鸿蒙双向绑定组件:TextArea、TextInput、Search、Checkbox,文本输入组件,图案解锁组件PatternLock
对象暂不支持双向绑定, 效果: 代码: Entry Component struct MvvmCase {StateisSelect: boolean falseStatesearchText: String ""StateinputText: string ""StateareaText: string ""build() {Grid() {G…...

JS 算法 - 计数器
theme: smartblue 题目描述 给定一个整型参数 n,请你编写并返回一个 counter 函数。这个 counter 函数最初返回 n,每次调用它时会返回前一个值加 1 的值 ( n , n 1 , n 2 ,等等)。 示例 1: 输入: n 10 ["cal…...

JavaScript基础——JavaScript运算符
赋值运算符 算术运算符 一元运算符 三元/三目运算符 比较运算符 逻辑运算符 运算符优先级 在JavaScript中,常见的运算符可以包括赋值运算符、一元运算符、算术运算符(二元运算符)、三元/三目运算符、比较运算符、逻辑运算符等࿰…...

E23.【C语言】练习:不创建第三个变量实现两个整数的交换
目录 题目条件 思路1( -) 思路2 (^)(XOR) 往期推荐 1.题目条件 禁止使用以上代码 2.思路1: -运算 aab; ba-b; aa-b; 但这样有潜在的问题 :a,b存储的数字过大,ab可能超过范围 因此改用思路2…...

如何搭建一个web系统?
需求 搭建一个web系统。 框架 设计:墨刀 前端:Vue.js 后端:Java 算法:Python 数据库:时序数据库,介绍 部署:Jekins https://www.jenkins.io/ 文档管理:Teambition 项目管理:禅道 代码管理:Gitlab 开发流程 设计文档和原型文档,功能接口设计࿰…...

三十种未授权访问漏洞复现 合集( 二 )
未授权访问漏洞介绍 未授权访问可以理解为需要安全配置或权限认证的地址、授权页面存在缺陷,导致其他用户可以直接访问,从而引发重要权限可被操作、数据库、网站目录等敏感信息泄露。---->目录遍历 目前主要存在未授权访问漏洞的有:NFS服务&a…...

C语言学习笔记[29]:函数①
函数 在C语言中,函数是一段可以完成特定功能的代码,它们可以被重复调用。 函数的分类: 库函数自定义函数 库函数 在C语言中,库函数是由系统提供的,用于完成特定功能的函数,这些函数被集合在一起&#…...

使用Springboot + netty 打造聊天服务之Nacos集群问题记录
目录 1、前言1.1、方法一1.2、方法二 2、方案二实战2.1、在netty服务里加上ws连接、中断事件2.2、在netty服务里加上消息服务 4、总结 使用Springboot netty 打造聊天服务系列文章 第一章 初始搭建工程 第二章 Nacos集群问题记录 1、前言 在使用Springboot Nacos Netty(Web…...
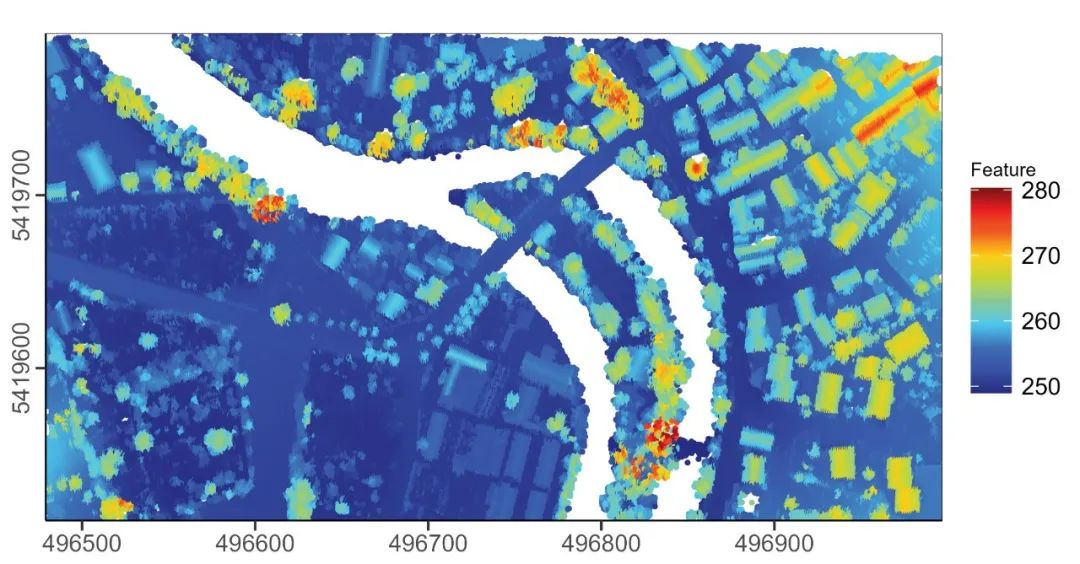
全网唯一!R语言顶刊配色包TheBestColors
与Matlab相比,R语言在绘图方面有着天然的优势。 比如在配色方面,R语言有各式各样现成的包,按理说配色这种事应该很方便才对。 但实际体验下来,发现似乎不是那么回事。 首先,你很难记住每个包的调用方法以及每种配色…...

链表题型思路错误总结
常见题目 206. 反转链表 关键点:定义前置指针。 在给cur.next复制前,需要定义好next节点防止断链。 public ListNode reverseList(ListNode head) {if (head null || head.next null) {return head;}ListNode pre null;ListNode cur head;while(cur…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
