E23.【C语言】练习:不创建第三个变量实现两个整数的交换
目录
题目条件
思路1(+ -)
思路2 (^)(XOR)
往期推荐
1.题目条件
禁止使用以上代码
2.思路1:+ -运算
a=a+b;
b=a-b;
a=a-b;但这样有潜在的问题 :a,b存储的数字过大,a+b可能超过范围
因此改用思路2
3.思路2:^运算(XOR)
复习异或运算:
异或运算==半加运算==不进位运算
0 XOR 0 == 0;0 XOR 1 == 1 XOR 0== 1; 1 XOR 1== 0 (1+1==10不进位,是0)
因此引出一系列定律:
归零定律:a XOR a == 0
恒等定律:a XOR 0 == a
交换定律:a XOR b == b XOR a
*(下面会用到)自反定律:a XOR b XOR a == b
*(下面会用到)结合定律:a XOR b XOR c == a XOR (b XOR c) == (a XOR b) XOR c
可以想到:
a=a^b;
b=a^b;
a=a^b;
解释:a=a XOR b; -->b=(a XOR b) XOR b == a XOR (b XOR b) == a XOR 0 == a 结合定律
-->a=a XOR b == (a XOR b) XOR a == a XOR b XOR a == b 自反定律
4.除此之外...
可以用汇编(这里以8086为例)利用栈交换数据
ax视作变量a,bx视作变量b
mov ax,1000
mov ss,ax
mov sp,0010 ;初始化栈顶
mov ax,001A
mov bx,001B
push ax
push bx
pop ax
pop bx
4.往期推荐
14.【C语言】初识操作符 上
15.【C语言】初识操作符 下
相关文章:

E23.【C语言】练习:不创建第三个变量实现两个整数的交换
目录 题目条件 思路1( -) 思路2 (^)(XOR) 往期推荐 1.题目条件 禁止使用以上代码 2.思路1: -运算 aab; ba-b; aa-b; 但这样有潜在的问题 :a,b存储的数字过大,ab可能超过范围 因此改用思路2…...

如何搭建一个web系统?
需求 搭建一个web系统。 框架 设计:墨刀 前端:Vue.js 后端:Java 算法:Python 数据库:时序数据库,介绍 部署:Jekins https://www.jenkins.io/ 文档管理:Teambition 项目管理:禅道 代码管理:Gitlab 开发流程 设计文档和原型文档,功能接口设计࿰…...

三十种未授权访问漏洞复现 合集( 二 )
未授权访问漏洞介绍 未授权访问可以理解为需要安全配置或权限认证的地址、授权页面存在缺陷,导致其他用户可以直接访问,从而引发重要权限可被操作、数据库、网站目录等敏感信息泄露。---->目录遍历 目前主要存在未授权访问漏洞的有:NFS服务&a…...

C语言学习笔记[29]:函数①
函数 在C语言中,函数是一段可以完成特定功能的代码,它们可以被重复调用。 函数的分类: 库函数自定义函数 库函数 在C语言中,库函数是由系统提供的,用于完成特定功能的函数,这些函数被集合在一起&#…...

使用Springboot + netty 打造聊天服务之Nacos集群问题记录
目录 1、前言1.1、方法一1.2、方法二 2、方案二实战2.1、在netty服务里加上ws连接、中断事件2.2、在netty服务里加上消息服务 4、总结 使用Springboot netty 打造聊天服务系列文章 第一章 初始搭建工程 第二章 Nacos集群问题记录 1、前言 在使用Springboot Nacos Netty(Web…...
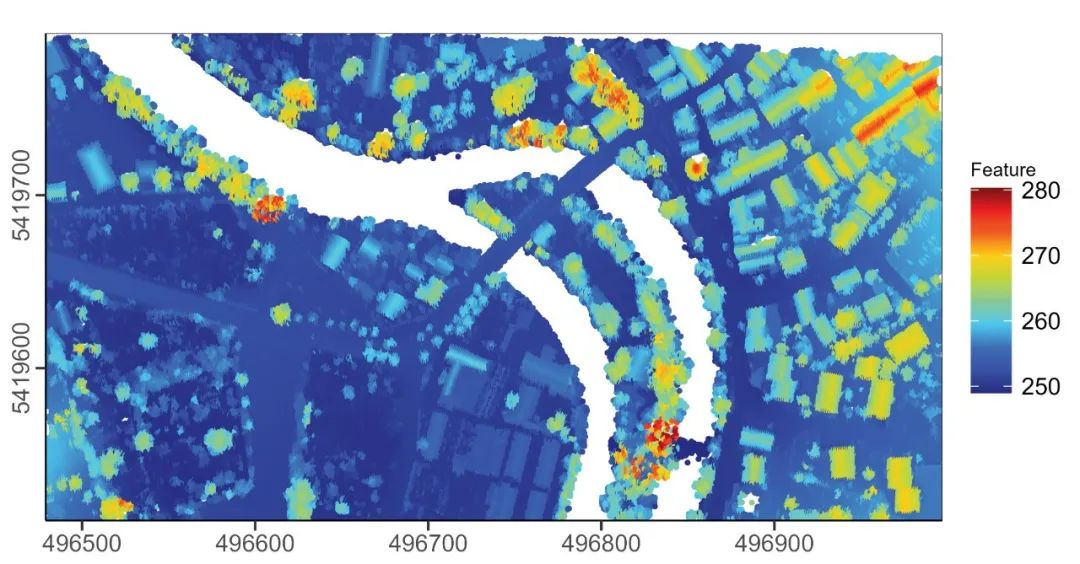
全网唯一!R语言顶刊配色包TheBestColors
与Matlab相比,R语言在绘图方面有着天然的优势。 比如在配色方面,R语言有各式各样现成的包,按理说配色这种事应该很方便才对。 但实际体验下来,发现似乎不是那么回事。 首先,你很难记住每个包的调用方法以及每种配色…...

链表题型思路错误总结
常见题目 206. 反转链表 关键点:定义前置指针。 在给cur.next复制前,需要定义好next节点防止断链。 public ListNode reverseList(ListNode head) {if (head null || head.next null) {return head;}ListNode pre null;ListNode cur head;while(cur…...

算法学习day28
一、寻找右区间(二分法) 题意:题目很容易理解 但是转换为二分法有点晦涩 给你一个区间数组 intervals ,其中 intervals[i] [starti, endi] ,且每个 starti 都 不同 。区间 i 的 右侧区间 可以记作区间 j ,并满足 startj > e…...
)
C语言基础题:迷宫寻路(C语言版)
1.题目描述 机器猫被困在一个矩形迷宫里。 迷宫可以视为一个n x m 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。 机器猫初始时位于(1,1)的位置,问能否走到(n,m)位置。 2.输入格式 第一行࿰…...

力扣-1两数之和2两数相加-2024/8/3
1、两数之和 解法一 暴力法(2个for循环) class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:for ii in range(len(nums)):for jj in range(ii1, len(nums)):if nums[ii]nums[jj] target:return [ii,jj]解法二 哈希表法…...

简站WordPress主题 专业的WordPress建站服务商
简站WordPress主题是一款备受推崇的WordPress主题,以其简洁、实用、无插件和更安全的特性脱颖而出。以下是关于简站WordPress主题的一些详细分析: 简站WordPress主题采用了扁平化设计风格,界面简洁明了,这使得网站看起来更加专业…...

Final Shell for Mac 虚拟机连接工具【简单易操作,轻松上手】【开发所需连接工具】
Mac分享吧 文章目录 效果一、下载软件二、安装软件三、运行测试安装完成!!! 效果 一、下载软件 下载软件 链接:http://www.macfxb.cn 二、安装软件 三、运行测试 安装完成!!!...

Oracle JDK:版本、支持与许可
文章目录 版本支持许可BCLOTNNFTCFAQ其他OpenJDK和其他的JDK实现JDK、JRE、JVMJava SE、Java EE、Java ME版本 Oracle JDK的最新版本和历史版本的官方下载地址(可查询版本发行说明等信息):https://www.oracle.com/cn/java/technologies/downloads/ 常规版本(非LTS):每隔…...

大模型学习笔记 - LLM 之RLHF人类对齐的简单总结
LLM - RLHF人类对齐的简单总结 LLM-人类对齐 1. RLHF(Reinforcement Learning from Human Feedback, RLHF),基于人类反馈的强化学习2 奖励模型训练3 强化学习训练 3.1 PPO介绍3.2 进阶的RLHF的介绍 3.2.1. 过程监督奖励模型3.2.2. 基于AI反馈的强化学习3.2.3. 非强化学习的对齐…...

【从零开始一步步学习VSOA开发】 概述
概述 概念 VSOA(Vehicle SOA)是翼辉为了解决任务关键型系统不能适用当前微服务通信架构问题而设计的⼀个轻量级适用于任务关键领域的微服务通信架构,以方便开发者构建大型分布式松耦合软件系统,且支持并行开发。 特点 其主要特…...

小程序背景图片无法通过 WXSS 获取
问题:pages/index/index.wxss 中的本地资源图片无法通过 WXSS 获取 可以使用网络图片,或者 base64,或者使用标签。 将图片转换为base64,地址 base64图片在线转换工具 - 站长工具 在这里把要使用的图片转换一把,然后将得…...

CC++内存魔术:掌控无形资源
hello,uu们,今天呢我们来详细讲解C&C的内存管理,好啦,废话不多讲,开干 1:C/C内存分布 2:C语言中动态内存管理方式:malloc/calloc/realloc/free 3:C内存管理方式 3.1:new/delete操作内置类型 3.1.1:代码1 3.1.2:代码2 3.2:new和delete操作自定义类型 3.2.1:C语言创建…...
算法--初阶
1、tips 1.1、set求交集 {1,2,3} & {2,3} & {1,2} {2} 其实就是位运算, 只有set可以这样使用, list没有这种用法 {1,2,3} | {2,3, 4} | {1,2} {1, 2, 3, 4} 并集 1.2、*与** * 序列(列表、元组)解包,如果是字典,那…...

通过Java实现插入排序(直接插入,希尔)与选择排序(直接选择,堆排)
目录 (一)插入排序 1.直接插入排序 (1)核心思想: (2)代码实现(以从小到大排序为例): (3)代码分析: 2.希尔排序(…...

大型分布式B2B2C多用户商城7.0企业版源码分享【java语言、方便二次开发】
项目介绍 项目基于SpringBoot开发,运营端和商户端采用ElementVue,买家使用采用VueIviewnuxt服务端渲染。使用到的中间件有Redis、RabbitMQ、ElasticSearch、FastDFS、Mongodb等。主要功能包括有运营管理、商品管理、订单管理、售后管理、会员管理、财务…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
