算法学习day28
一、寻找右区间(二分法)
题意:题目很容易理解 但是转换为二分法有点晦涩
给你一个区间数组 intervals ,其中 intervals[i] = [starti, endi] ,且每个 starti 都 不同 。区间 i 的 右侧区间 可以记作区间 j ,并满足 startj >= endi ,且 startj 最小化 。注意 i 可能等于 j 。
让我们去找一个区间的最小右侧区间,满足条件:右侧区间的start值>该区间的end值,可能存在多个右侧区间,取最小的start值的区间。并把该区间的下标放到数组里面返回。没有记作-
思路:
题目要让我们去找一个区间的最小右侧区间。如何做到最小?
1.首先将每个区间的start值进行排序
2.然后for循环遍历每一个区间,将其end值作为target。
3.然后二分查找第一个>=target的start值的下标。放到res数组中
4.返回res数组
代码:
//将每一个区间的左端点排序 遍历每一个数组的右端点 找到第一个比它大的左端点 然后加入到集合中。如何将左端点排序,使用二维数组
class Solution {public int[] findRightInterval(int[][] intervals) {//第一步 创建sortStart数组 并且排序int[][] sortStart=new int[intervals.length][2];//start值:下标for(int i=0;i<intervals.length;i++){sortStart[i]=new int[]{intervals[i][0],i};}Arrays.sort(sortStart,(a,b)->a[0]-b[0]);//第二步 遍历每一个区间的end 并且将其作为targetint[] res=new int[intervals.length];for(int i=0;i<intervals.length;i++){int target=intervals[i][1];//第i个区间的end值int left=0,right=sortStart.length-1;//第三步 二分查找最小的>=end的start值的下标 放入res数组中while(left<right){int mid=left+(right-left)/2;if(sortStart[mid][0]>=target){right=mid;}else{left=mid+1;}}res[i]=sortStart[left][0]>=intervals[i][1]?sortStart[left][1]:-1;}return res;}
}二、最长递增子序列(dp+二分法)
解法一:dp动态规划
dp五部曲:
1.dp[i]的含义:以i为结尾的最长递增子序列的长度
2.递推公式:dp[i]=Math.max(dp[i],dp[j]+1);在0->i,如果找到比nums[i]小的数,说明找到了一个递增序列,然后对dp[i]进行更新。
3.初始化dp[i]=1;
4.遍历的顺序:双层for循环,i从1开始,j从0开始直j<i;
代码:
class Solution {public int lengthOfLIS(int[] nums) {//1.dp[i]:以i结尾的最长递增子序列的长度int[] dp=new int[nums.length];Arrays.fill(dp,1);int max=1;for(int i=1;i<nums.length;i++){for(int j=0;j<i;j++){if(nums[j]<nums[i]){dp[i]=Math.max(dp[i],dp[j]+1);}}max=Math.max(max,dp[i]);}return max;}
}解法二:辅助数组+二分法
思路:
遍历数组,如果遇到的数字是大于尾部元素的,直接放到尾部元素后面,使得递增序列变大;
如果遇到的数字是小于尾部元素的,为了使递增的速度最慢,就要将该元素放到最合适的地方.
那么这个最合适的地方如何去寻找? 当然我们可以利用辅助数组单调递增的规律,使用二分查找法去寻找最合适的地方。
代码:
class Solution {public int lengthOfLIS(int[] nums) {//1.定义辅助数组int[] sortNums=new int[nums.length];int size=1;sortNums[0]=nums[0];for(int i=0;i<nums.length;i++){//如果大于的话 直接放到sortNums的后边if(nums[i]>sortNums[size-1]){sortNums[size++]=nums[i];}else{//如果小于的话 我们就要去找合适的位置int target=nums[i];int left=0,right=size-1;while(left<=right){int mid=left+(right-left)/2;if(sortNums[mid]>=target){right=mid-1;}else{left=mid+1;}}sortNums[right+1]=nums[i];}}return size;}
}三、寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设 nums[-1] = nums[n] = -∞ 。
因为nums[-1]=nums[n]=-∞;因此可以推断出:
nums[i]<nums[i+1]:那么后面一定存在一个峰值;
nums[i]>=nums[i+1];那么前面一定存在一个峰值;
思路:
那么就根据推断出的规律来进行二分查找:如果nums[mid]>=nums[mid+1] left=mid+1;
nums[mid]<nums[mid+1] right=mid;
代码:
class Solution {public int findPeakElement(int[] nums) {if(nums.length==1)return 0;int left=0,right=nums.length-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]>=nums[mid+1]){right=mid;}else{left=mid+1;}}return left;}
}四、找到k个最接近的元素
题意:
给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。
输入:arr = [1,2,3,4,5], x = 3, k = 4 输出:[1,2,3,4] 相同距离的话 加入较小的
解法一:双指针删除法
思路:
逆向思维,在数组中删除(size-k)个离x最远的数字。可以使用双指针(left,right)向x靠近的同时不断删除元素。
比如在1 2 3 4 5中寻找4个最靠近3的数。
left指向1,right指向5。和3的距离都为2,将5删除。剩余四个数字 4==k。那么加入到集合中返回。
代码:
class Solution {public List<Integer> findClosestElements(int[] arr, int k, int x) {// 双指针删除法List<Integer> res = new ArrayList<>();int number = arr.length;int left = 0;int right = number - 1;int count = 0;while (left <= right) {if (count == number - k) {for (int i = left; i <= right; i++) {res.add(arr[i]);}}int diff1 = Math.abs(x - arr[left]);int diff2 = Math.abs(arr[right] - x);if (diff1 <= diff2)right--;elseleft++;count++;// 已经删除的数字}return res;}
}五、俄罗斯套娃问题(最长上升子序列的二维版)
你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
解法一:动态规划(超时)
解法二:贪心+二分查找
思路:
当只有宽和高都比上一个信封大的时候,才能实现套娃。
我们可以先对宽度进行升序排列,确认了宽度之后,就变成一维的求最长上升子序列了。
如何求最大长度的高度序列。使用贪心算法:每次我们都希望放在末尾的值是一个符合条件并且尽可能小的数字,这样我们的长度最长的概率就最大。(因此当我们遇到heights[i]<tails[size]的时候,我们需要将heights[i]放到合适的位置,但是heights所对应宽度是可能相等的。在相等的时候,我们应该按照降序排列,这样在更新下一个的时候就会把它刷掉)。
举个例子理解一下:假如按照升序排列后为:(5,5),(6,6),(7,2)(7,1)(8,3),(9,4)。
1.envelopes[i][1]=5, 集合为空,tails[0]=5 size=1;
2.envelopes[i][1]=6, 6大于5,tails[1]=6,size=2;
3.envelopes[i][1]=2, 2小于6,给2寻找合适的位置,2<5。因此tails[0]=2;
4.envelopes[i][1]=1, 1小于6,给1寻找合适的位置,1<2,因此tails[0]=1;
5.envelopes[i][1]=3,3小于6,给3寻找合适的位置,3<6,因此tails[1]=3;
6.envelopes[i][1]=4,4大于3,因此tails[2]=4;size=3
寻找合适的位置是根据二分搜索法进行寻找。
代码:
class Solution {public int maxEnvelopes(int[][] envelopes) {if(envelopes.length==0)return 0;;// 对信封的宽度排序Arrays.sort(envelopes,new Comparator<int[]>(){public int compare(int[] a,int[] b){return a[0]==b[0]?b[1]-a[1]:a[0]-b[0];}});int maxSize=1;int size=1;int[] tails=new int[envelopes.length];tails[0]=envelopes[0][1];for(int i=1;i<envelopes.length;i++){if(envelopes[i][1]>tails[size-1]){tails[size++]=envelopes[i][1];}else{int left=0,right=size-1;int target=envelopes[i][1];while(left<=right){int mid=left+(right-left)/2;if(tails[mid]>=target)right=mid-1;else left=mid+1;}tails[right+1]=target;}}return size;}
}六、寻找旋转排序数组中的最小值(要求时间复杂度为O(logN))
思路:二分法
旋转之前,是一个升序数组;旋转之后,会变成两段升序数组。
旋转时,小数往后走,大数旋转到前面来。分情况:
1.起始点在到达中间之前,(右边部分一定处于升序),nums[mid]的值一定是小于nums[right]的,此时起始点一定在mid左边(包括mid)
2.起始点到达中间之后,大数占领起始点之前的区域,nums[mid]的值一定是大于nums[right]的,此时起始点一定是在右半部分的。(反证一下,如果起始点在左部分的话,那么起始点的右边一定是升序的,那么nums[mid]一定小于nums[right])
所以
1.当nums[mid]>nums[right],起始点一定在右边,更新左边界left=mid+1;
2.当nums[mid]<=nums[right],起始点一定在左边,更新有边界right=mid;
代码:
class Solution {public int findMin(int[] nums) {int size=nums.length;int left=0,right=size-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<nums[right]){right=mid;}else{left=mid+1;}}return nums[left];}
}七、搜索旋转排序数组
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
思路:
将一个排序好的数组旋转,变成两段升序序列(也可能是一段 就是原始的)。然后找到元素的起始点。两种情况:
1.如果起始点==0,说明并没有进行旋转,还是原始的数组。
2.如果起始点>0,说明进行了旋转,在两段序列中进行查找target就可以。
代码:
class Solution {public int search(int[] nums, int target) {if (nums.length == 1 && nums[0] == target)return 0;// 首先找到起始点 找到起始点之后 两段升序找targetint left = 0, right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] <= nums[right]) {// 说明mid一定在左半边right = mid;} else {left = mid + 1;}}// left就是起始的位置int res1 = 0;int res2 = 0;if (left == 0)return binarySearch(nums, 0, nums.length - 1, target);else {res1 = binarySearch(nums, 0, left - 1, target);res2 = binarySearch(nums, left, nums.length - 1, target);}return res1 == -1 ? res2 : res1;}public int binarySearch(int[] nums, int left, int right, int target) {int index = -1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > target) {right = mid;} else if (nums[mid] < target) {left = mid + 1;} else {return mid;}}return nums[left]==target?left:index;}
}八、搜索二维矩阵II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。

思路:
如果从左上角或者右下角开始寻找的话,不具有区别度。
如果从右上角或者左下角寻找的话:
1.右上角:左边变小,下边变大
2.左下角:上边变小,右边变大
代码:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {//从右上角出发int rol=matrix.length;int cow=matrix[0].length;int x=0,y=cow-1;while(x<rol&&y>=0){if(matrix[x][y]<target){x++;}else if(matrix[x][y]>target){y--;}else{return true;}}return false;}
}相关文章:

算法学习day28
一、寻找右区间(二分法) 题意:题目很容易理解 但是转换为二分法有点晦涩 给你一个区间数组 intervals ,其中 intervals[i] [starti, endi] ,且每个 starti 都 不同 。区间 i 的 右侧区间 可以记作区间 j ,并满足 startj > e…...
)
C语言基础题:迷宫寻路(C语言版)
1.题目描述 机器猫被困在一个矩形迷宫里。 迷宫可以视为一个n x m 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。 机器猫初始时位于(1,1)的位置,问能否走到(n,m)位置。 2.输入格式 第一行࿰…...

力扣-1两数之和2两数相加-2024/8/3
1、两数之和 解法一 暴力法(2个for循环) class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:for ii in range(len(nums)):for jj in range(ii1, len(nums)):if nums[ii]nums[jj] target:return [ii,jj]解法二 哈希表法…...

简站WordPress主题 专业的WordPress建站服务商
简站WordPress主题是一款备受推崇的WordPress主题,以其简洁、实用、无插件和更安全的特性脱颖而出。以下是关于简站WordPress主题的一些详细分析: 简站WordPress主题采用了扁平化设计风格,界面简洁明了,这使得网站看起来更加专业…...

Final Shell for Mac 虚拟机连接工具【简单易操作,轻松上手】【开发所需连接工具】
Mac分享吧 文章目录 效果一、下载软件二、安装软件三、运行测试安装完成!!! 效果 一、下载软件 下载软件 链接:http://www.macfxb.cn 二、安装软件 三、运行测试 安装完成!!!...

Oracle JDK:版本、支持与许可
文章目录 版本支持许可BCLOTNNFTCFAQ其他OpenJDK和其他的JDK实现JDK、JRE、JVMJava SE、Java EE、Java ME版本 Oracle JDK的最新版本和历史版本的官方下载地址(可查询版本发行说明等信息):https://www.oracle.com/cn/java/technologies/downloads/ 常规版本(非LTS):每隔…...

大模型学习笔记 - LLM 之RLHF人类对齐的简单总结
LLM - RLHF人类对齐的简单总结 LLM-人类对齐 1. RLHF(Reinforcement Learning from Human Feedback, RLHF),基于人类反馈的强化学习2 奖励模型训练3 强化学习训练 3.1 PPO介绍3.2 进阶的RLHF的介绍 3.2.1. 过程监督奖励模型3.2.2. 基于AI反馈的强化学习3.2.3. 非强化学习的对齐…...

【从零开始一步步学习VSOA开发】 概述
概述 概念 VSOA(Vehicle SOA)是翼辉为了解决任务关键型系统不能适用当前微服务通信架构问题而设计的⼀个轻量级适用于任务关键领域的微服务通信架构,以方便开发者构建大型分布式松耦合软件系统,且支持并行开发。 特点 其主要特…...

小程序背景图片无法通过 WXSS 获取
问题:pages/index/index.wxss 中的本地资源图片无法通过 WXSS 获取 可以使用网络图片,或者 base64,或者使用标签。 将图片转换为base64,地址 base64图片在线转换工具 - 站长工具 在这里把要使用的图片转换一把,然后将得…...

CC++内存魔术:掌控无形资源
hello,uu们,今天呢我们来详细讲解C&C的内存管理,好啦,废话不多讲,开干 1:C/C内存分布 2:C语言中动态内存管理方式:malloc/calloc/realloc/free 3:C内存管理方式 3.1:new/delete操作内置类型 3.1.1:代码1 3.1.2:代码2 3.2:new和delete操作自定义类型 3.2.1:C语言创建…...
算法--初阶
1、tips 1.1、set求交集 {1,2,3} & {2,3} & {1,2} {2} 其实就是位运算, 只有set可以这样使用, list没有这种用法 {1,2,3} | {2,3, 4} | {1,2} {1, 2, 3, 4} 并集 1.2、*与** * 序列(列表、元组)解包,如果是字典,那…...

通过Java实现插入排序(直接插入,希尔)与选择排序(直接选择,堆排)
目录 (一)插入排序 1.直接插入排序 (1)核心思想: (2)代码实现(以从小到大排序为例): (3)代码分析: 2.希尔排序(…...

大型分布式B2B2C多用户商城7.0企业版源码分享【java语言、方便二次开发】
项目介绍 项目基于SpringBoot开发,运营端和商户端采用ElementVue,买家使用采用VueIviewnuxt服务端渲染。使用到的中间件有Redis、RabbitMQ、ElasticSearch、FastDFS、Mongodb等。主要功能包括有运营管理、商品管理、订单管理、售后管理、会员管理、财务…...
)
C++的结构体、联合体、枚举类型(一)
1.C++的结构体 2.C++的联合体 3.C++的枚举类型 1.C++的结构体 (1)C++中定义结构体变量,可以省略struct关键字 struct XX{…}; XX x;//定义结构体变量直接省略struct(2)C++结构体中可以直接定义函数,谓之成员函数(又叫方法)(3)在成员函数中可以直接访问该结构体的成员变…...
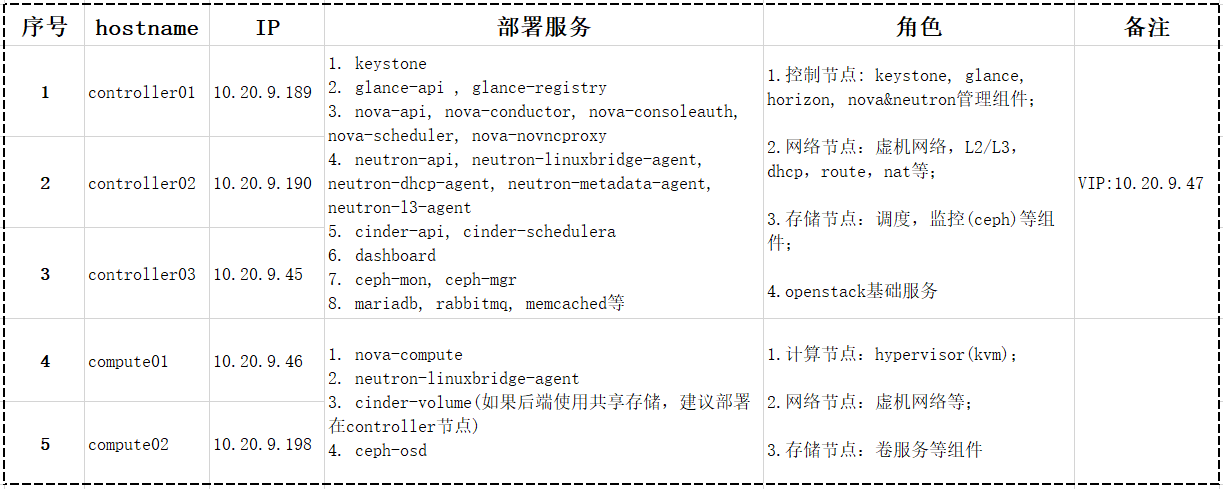
搭建高可用OpenStack(Queen版)集群(一)之架构环境准备
一、搭建高可用OpenStack(Queen版)集群之架构环境准备 一、架构设计 二、初始化基础环境 1、管理节点创建密钥对(方便传输数据) 所有控制节点操作 # ssh-keygen #一路回车即可 Generating public/private rsa key pair. Enter f…...
通过Stack Overflow线程栈溢出的问题实例,详解C++程序线程栈溢出的诸多细节
目录 1、问题说明 2、从Visual Studio输出窗口中找到了线索,发生了Stack Overflow线程栈溢出的异常 3、发生Stack Overflow线程栈溢出的原因分析 4、线程占用的栈空间大小说明 5、引发线程栈溢出的常见原因和场景总结 6、在问题函数入口处添加return语句&…...

LeetCode刷题笔记 | 3 | 无重复字符的最长子串 | 双指针 | 滑动窗口 | 2025兴业银行秋招笔试题 | 哈希集合
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 这是一道银行的面试题,就是简单?! LeetCode链接:3. 无重复字符的最长子串 1.题目描述 给定一个字符串 s ,…...

验证cuda和pytorch都按照成功了
要验证您的PyTorch是否能够调用CUDA,您可以执行以下步骤: 1. **检查CUDA是否可用**: 在Python中运行以下代码来检查CUDA是否可用: python import torch print(torch.cuda.is_available()) 如果输出为 True&…...

iOS开发如何自己捕获Crash
为了在iOS中捕获和处理未捕获的Objective-C异常和系统信号引起的崩溃,可以使用NSSetUncaughtExceptionHandler和标准的Unix信号处理机制来实现。这能帮助你记录绝大部分的崩溃信息。以下是详细的实现步骤和代码示例: 一、系统崩溃处理 通过NSSetUncaug…...
)
雪花算法(Snowflake Algorithm)
雪花算法(Snowflake Algorithm)是一种分布式唯一ID生成算法,主要用于生成全球唯一的ID,广泛应用于分布式系统中,例如在数据库中作为主键。这个算法最初由Twitter提出,并且被广泛使用在很多大规模系统中。有…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
