Studying-代码随想录训练营day56| 108.冗余连接、109.冗余连接II
第56天,图论06,并查集题目类型冗余连接(ง •_•)ง💪,编程语言:C++
目录
108.冗余连接
109.冗余连接II
总结
108.冗余连接
文档讲解:手撕冗余连接
题目:108. 冗余连接 (kamacoder.com)


学习:本题也可以用并查集的方法进行求解。原因在于要使得删除一条边后,图变为一棵树,也即只有一个根节点。
只有一个根节点也就意味着大家都在一个集合之中。因此我们可以采取从前向后遍历的顺序,遍历每一条边,边的两个节点如果不再同一个集合,就加入集合。
如果在同一个集合,那就说明这条边的两个节点,已经连通了,加入这条边一定会出现环,则需要将这条边删除。(并且事实上在我们发现这条边的时候,就已经是我们找到的答案中的最后出现的边了,因为我们是从前往后遍历的,遍历到这条边,就已经是必须要删除的状态了)
代码:先写出并查集模板,然后进行求解
#include <iostream>
#include <vector>
using namespace std;//并查集模版
int n;
vector<int> father(n + 1, 0); //节点从1开始,因此我们定义一个n+1大小的数组void init() { //初始化father数组for(int i = 0; i <= n; i++) {father[i] = i;}
}int find(int u) { //寻根函数// return u == father ? u : father[u] = find(father[u]); //简化写法if(u == father[u]) return u; //自身就是根return father[u] = find(father[u]); //假如路径压缩
}bool isSame(int u, int v) { //判断是否在一个集合当中u = find(u);v = find(v);return u == v;
}void join(int u, int v) { //将两个点加入一个集合u = find(u); //找到根v = find(v); //找到根if(u == v) return; //本身就已经在一个集合中了father[v] = u;
}int main() {cin >> n;init(); //初始化数组int s, t;for (int i = 0; i < n; i++) { //进行并查集合并cin >> s >> t;if (isSame(s, t)) {cout << s << " " << t << endl;return 0;} else {join(s, t);}}return 0;
}109.冗余连接II
文档讲解:手撕冗余连接II
题目:109. 冗余连接II (kamacoder.com)


学习:本题是将无向图转变为有向图,相对的会复杂一些。但我们需要明确,本题中的有向图,指的是一颗有向树+一条有向边组成的。同时有向树的特点在于,只有根节点的入度为0,其他节点入度都为1。
基于此我们可以考虑两种情况:第一种情况有一个节点的入度为2;第二种情况存在环(即没有入度为0的根节点)
第一种情况又可以分为两种情形:
1.如果我们找到入度为2的点,那么删除一条指向该节点的边就行。以下图为例,删1 -> 3 或者 2 -> 3都可以,选择删除顺序靠后便可。

2.入度为2也有另一种情况,只能删除特定的一条边。以下图为例,只能删除边1->3,另一条边是不可以删除的,会丢失一个点。

第二种情况没有入度为2的点,而是存在环。以下图为例,删除构成环的边,使得到一个入度为0的根节点即可。

分析好了以上三种情形之后,我们就可以针对性的进行代码的书写。
针对第一种情况:我们可以统计每个节点的度,找寻是否有节点度为2的节点。
int s, t;vector<vector<int>> edges;cin >> n;vector<int> inDegree(n + 1, 0); // 记录节点入度for (int i = 0; i < n; i++) {cin >> s >> t;inDegree[t]++;edges.push_back({s, t});}
如果有的话,一定是删除指向入度为2的节点的两条边其中的一条,如果删了一条,判断这个图是一个树,则这条边就是答案(同时我们还要保证是从前往后遍历的,以便于我们删除最后一条边)
vector<int> vec; // 记录入度为2的边(如果有的话就两条边)
// 找入度为2的节点所对应的边,注意要倒序,因为优先删除最后出现的一条边
for (int i = n - 1; i >= 0; i--) {if (inDegree[edges[i][1]] == 2) {vec.push_back(i);}
}
if (vec.size() > 0) {// 放在vec里的边已经按照倒叙放的,所以这里就优先删vec[0]这条边if (isTreeAfterRemoveEdge(edges, vec[0])) {cout << edges[vec[0]][0] << " " << edges[vec[0]][1];} else {cout << edges[vec[1]][0] << " " << edges[vec[1]][1];}return 0;
}而对于第二种情况也就是出现环的情况,则我们按照上一题的办法,找到成环的边即可。
// 在有向图里找到删除的那条边,使其变成树
void getRemoveEdge(const vector<vector<int>>& edges)接下来我们就是要实现 isTreeAfterRemoveEdge()和getRemoveEdge(),这两个函数了。
第一个函数用于判断删除一个边之后是不是有向树,方法是通过将所有边的两端节点加入并查集,遇到要删除的边则跳过,只有删除了正确的边,才能够将所有节点都加入并查集。否则会出现丢失点,并且另外的点成环的情况。
第二个函数则是确定了有环,则我们只需要将所有边的两端节点加入并查集,并且从前往后,直到遇到第一个使得并查集出现重复的边,则说明这条边是要删除的边。
由此可以看出这两个函数的实现,其实都可以是在上一题基础上进行实现的。
代码:在并查集的基础上,加入两函数
#include <iostream>
#include <vector>
using namespace std;//并查集模版
int n;
vector<int> father(1001, 0); //节点从1开始,因此我们定义一个n+1大小的数组void init() { //初始化father数组for(int i = 0; i <= n; i++) {father[i] = i;}
}int find(int u) { //寻根函数// return u == father ? u : father[u] = find(father[u]); //简化写法if(u == father[u]) return u; //自身就是根return father[u] = find(father[u]); //假如路径压缩
}bool isSame(int u, int v) { //判断是否在一个集合当中u = find(u);v = find(v);return u == v;
}void join(int u, int v) { //将两个点加入一个集合u = find(u); //找到根v = find(v); //找到根if(u == v) return; //本身就已经在一个集合中了father[v] = u;
}// 删一条边之后判断是不是树
bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {init(); // 初始化并查集for (int i = 0; i < n; i++) {if (i == deleteEdge) continue; //跳过删除的边if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树return false;}join(edges[i][0], edges[i][1]);}return true;
}// 在有向图里找到删除的那条边,使其变成树
void getRemoveEdge(const vector<vector<int>>& edges) {init(); // 初始化并查集for (int i = 0; i < n; i++) { // 遍历所有的边if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边cout << edges[i][0] << " " << edges[i][1];return;} else {join(edges[i][0], edges[i][1]);}}
}int main() {cin >> n;int s, t;vector<vector<int>> edges; //保存边vector<int> inDegree(n + 1, 0); // 记录节点入度for (int i = 0; i < n; i++) {cin >> s >> t;inDegree[t]++; //t是入度edges.push_back({s, t});}vector<int> vec; // 记录入度为2的边(如果有的话就两条边)// 找入度为2的节点所对应的边,注意要倒序,因为优先删除最后出现的一条边for (int i = n - 1; i >= 0; i--) { //从后往前,保证边是倒叙进入的,以便于输出最后一条边if (inDegree[edges[i][1]] == 2) {vec.push_back(i); //把边的序号加入}}// 第一种情况if (vec.size() > 0) {// 放在vec里的边已经按照倒叙放的,所以这里就优先删vec[0]这条边if (isTreeAfterRemoveEdge(edges, vec[0])) { //判断当前边删除可不可以,如果不可以,则一定时删除另一条边cout << edges[vec[0]][0] << " " << edges[vec[0]][1];} else {cout << edges[vec[1]][0] << " " << edges[vec[1]][1];}return 0;}// 第二种情况getRemoveEdge(edges);return 0;
}总结
今天的两道题,是对并查集的巩固考察。第二道题增加了对有向图的分析,但实际上还是使用了并查集具备的查找两个元素是否在一个集合,查找成环的能力。需要多加练习!!!
相关文章:

Studying-代码随想录训练营day56| 108.冗余连接、109.冗余连接II
第56天,图论06,并查集题目类型冗余连接(ง •_•)ง💪,编程语言:C 目录 108.冗余连接 109.冗余连接II 总结 108.冗余连接 文档讲解:手撕冗余连接 题目:108. 冗余连接 (kamacoder.com) 学习&…...

基于springboot+vue+uniapp的智慧物业平台小程序
开发语言:Java框架:springbootuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包&#…...

MATLAB霍夫曼表盘识别系统
MATLAB霍夫曼表盘识别系统 一、介绍 本设计为基于MATLAB的表盘指针识别,算法原理是基于hough变换。可检测压力表,石英手表,电表刻度,气压表等带指针刻度的表盘。通过hough检测直线和圆的关系,得出指针夹角࿰…...

Python | Leetcode Python题解之第322题零钱兑换
题目: 题解: class Solution:def coinChange(self, coins: List[int], amount: int) -> int:dp [float(inf)] * (amount 1)dp[0] 0for coin in coins:for x in range(coin, amount 1):dp[x] min(dp[x], dp[x - coin] 1)return dp[amount] if d…...

python中类class的魔法方法
开始介绍之前,我们先看下之前文章我们介绍过的内置类merryview的一些方法,如下图所示: 有很多双下划线开始和结束的method,这么多method是做啥子用的呢? 其实这些方法就是我们常说的魔法方法,也是python中的…...

计算机体系结构和计算机组成原理的区别
如何理解计算机体系结构和计算机的组成?哪个对计算机的性能更重要?说明理由 目录 计算机体系结构 计算机组成 二者区别 哪个对性能更重要 计算机体系结构 计算机体系结构是指根据属性和功能不同而划分的计算机理论组成部分及计算机基本工作原理、理论…...

MySQL--数据库备份
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 一、为什么要备份 备份:能够防止由于机械故障以及人为误操作带来的数据丢失,例如将数据库文件保存在了其它地方。 冗余&#…...

influxDB的常用命令
目录 1.查看数据库命令 2.进入某数据库命令 3.创建表的命令 (host 和region 字段是必须的) 4.显示所有的表命令 5. 删除表 6.查询表数据 7.显示数据库用户 8.创建用户 9.创建管理员用户 10.修改密码(密码用单引号括住,不要用双引号) 11. 分配数据库访问权…...

使用 1panel面板 部署 springboot 和 vue
代码仓库:还没弄 目录 网站介绍安装步骤1. 准备云服务器2. 准备域名(可跳过)3. 安装1panel面板4. 服务器开放端口5. 进入1panel面板6. 安装并启动软件(服务器和面板开放端口)7. 打包并上传项目7.1 打包 Java项目&#…...

快速体验LLaMA-Factory 私有化部署和高效微调Llama3模型(曙光超算互联网平台异构加速卡DCU)
序言 本文以 LLaMA-Factory 为例,在超算互联网平台SCNet上使用异构加速卡AI 显存64GB PCIE,私有化部署Llama3模型,并对 Llama3-8B-Instruct 模型进行 LoRA 微调、推理和合并。 快速体验基础版本,请参考另一篇博客:快…...

Cocos Creator 3.8.x bundle设置最佳方案
A: 项目开始场景(Start Scene)加载显示最快的Bundle设置方案:不要使用resources文件夹,除了项目开始场景(Start Scene)所在文件夹,将所有文件分类设置成Bundle; B: A方案较为麻烦,项目文件夹多时…...

【论文笔记】4D Millimeter-Wave Radar in Autonomous Driving: A Survey
原文链接:https://arxiv.org/abs/2306.04242 I. 引言 传统毫米波雷达(3D毫米波雷达)测量俯仰角的能力有限,数据通常仅包括距离、水平角和多普勒速度信息。此外,3D雷达数据存在噪声且分辨率低(尤其是水平角…...
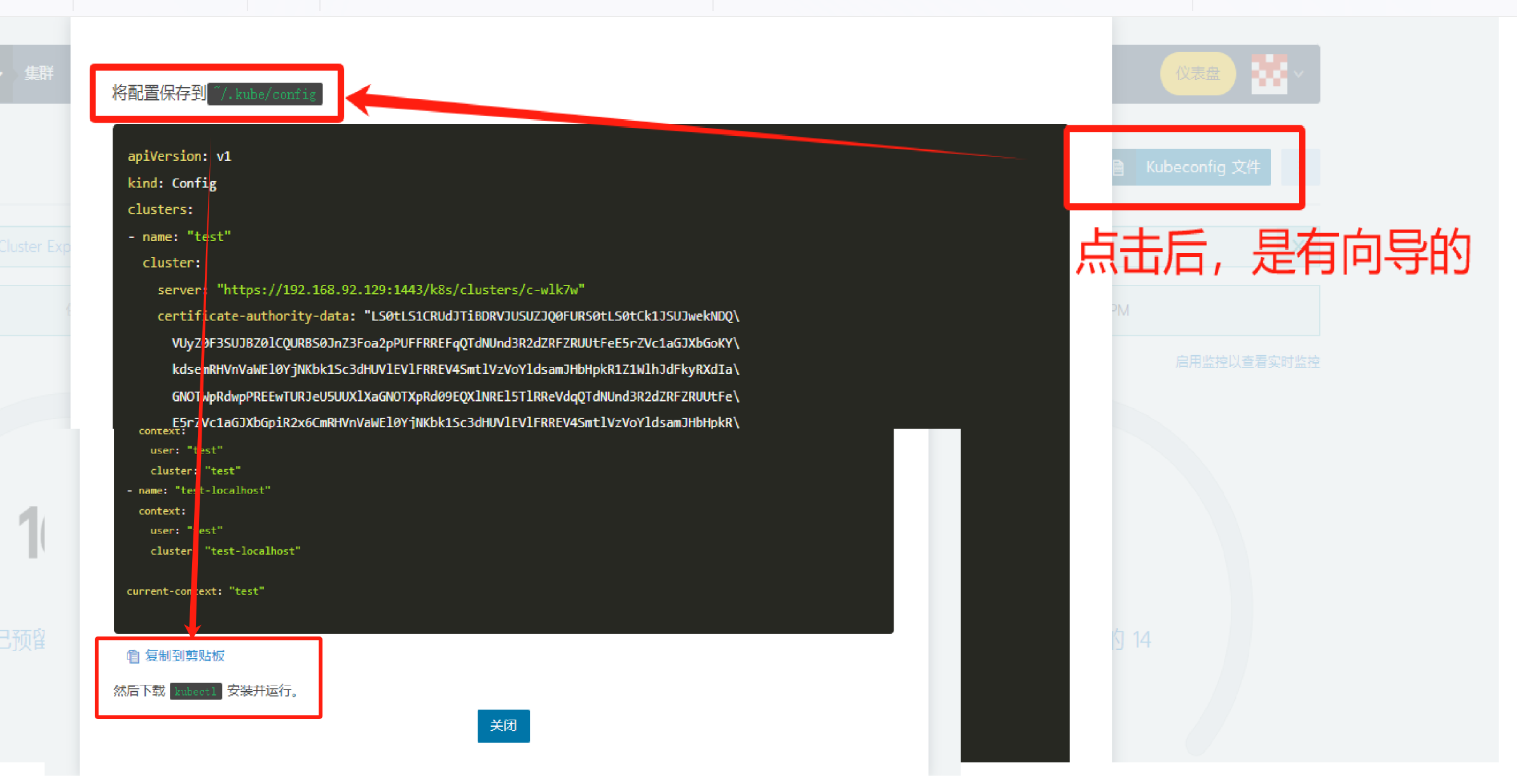
搭建 Rancher 服务,配置k8s集群
1. 前提条件 前提条件: 安装docker,要求版本各节点版本一致。网上还有额外的要求:关闭swap、禁用selinux等等。 2. 搭建 Rancher 服务 直接通过docker命令实现即可,很方便。 docker run -d \--name rancher \--restart unles…...

数据恢复的定制之旅:打造SQL Server的专属恢复方案
数据恢复的定制之旅:打造SQL Server的专属恢复方案 在企业运营中,数据的安全性和可靠性是至关重要的。SQL Server作为企业级数据库解决方案,提供了多种数据恢复技术以应对不同的数据丢失场景。然而,面对特定的业务需求和复杂的数…...

Javascript常见算法详解
在JavaScript(JS)中,常见的算法涵盖了多个领域,从基础的数组操作到更复杂的排序、搜索和数据结构算法。下面是一些在JS中常见的算法示例: 1. 排序算法 Java排序算法-CSDN博客 冒泡排序(Bubble Sort&#x…...

MySQL数据管理 - 查询语句
文章目录 查询数据1 查询指定列2 条件查询3 合并查询4 模糊查询5 聚合函数查询6 对值进行排序7 分组查询8 分页查询9 数据库关联查询1 内连接 INNER JOIN2 LEFT JOIN3 右连接 10 数据库子查询参考 查询数据 数据库最常用的操作就是查询,也是数据操作的基础…...

经典图论算法回顾之Bellman-Ford算法
Dijkstra最短路径算法存在的一个问题是不能处理负权图(详见:经典图论算法回顾之Dijkstra算法。今天要回顾的Bellman-Ford算法(wikipedia:Bellman–Ford algorithm)可以求出有负权图的最短路径,并可以对最短…...

LinuxC++(10):调用可执行程序
认识system函数 可以直接用system在代码中实现调用shell命令 /bin/ls -l /tmp表示执行ls -l命令,打开/tmp地址 而前面的/bin/表示这是shell命令,不可少,可以认为,/bin/后面的就是等价于shell里面输入的命令。 然后,cou…...

C语言指针·高级用法超详解(指针运算、野指针、悬空指针、void类型指针、二级以及多级指针)
目录 1. 指针的运算 2. 野指针和悬空指针 2.1 野指针 2.2 悬空指针 3. void类型指针 4. 二级指针和多级指针 4.1 命名规则 4.2 作用 4.2.1 二级指针可以操作一级指针记录的地址 4.2.2 利用二级指针获取变量中记录的数据 1. 指针的运算 文章开始前可以先了…...

SQL注入:MySQL元数据库,外网实战手工SQL注入
MySQL元数据库 MySQL的元数据库是一组特殊的数据库,用于存储MySQL服务器的元数据信息,在sql注入中较为常用为以下两种元数据库: information_schema:这个数据库包含了MySQL服务器上所有其他数据库的元数据信息。例如数据库名、表…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
