力扣刷题之3128.直角三角形
题干描述
给你一个二维 boolean 矩阵 grid 。
请你返回使用 grid 中的 3 个元素可以构建的 直角三角形 数目,且满足 3 个元素值 都 为 1 。
注意:
- 如果
grid中 3 个元素满足:一个元素与另一个元素在 同一行,同时与第三个元素在 同一列 ,那么这 3 个元素称为一个 直角三角形 。这 3 个元素互相之间不需要相邻。
示例 1:
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
输入:grid = [[0,1,0],[0,1,1],[0,1,0]]
输出:2
解释:
有 2 个直角三角形。
示例 2:
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 |
输入:grid = [[1,0,0,0],[0,1,0,1],[1,0,0,0]]
输出:0
解释:
没有直角三角形。
示例 3:
| 1 | 0 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
输入:grid = [[1,0,1],[1,0,0],[1,0,0]]
输出:2
解释:
有两个直角三角形。
题干描述
问题理解
我们需要在一个二维布尔矩阵grid中统计由1组成的直角三角形的数量。一个直角三角形由三个元素组成,要求:
- 一个元素与另一个元素在同一行。
- 这个元素还需要与第三个元素在同一列。
这些组成三角形的元素之间不需要相邻。
解题思路
为了解决这个问题,我们需要系统地检查矩阵中的每一个位置,看它是否能作为直角三角形直角顶点。具体步骤如下:
1.统计行和列中i的数量
- 对于矩阵中的内个单元格,计算它所在的行和列中1的数量。的数量。这有助于我们确定可以形成三角形的水平和垂直线。
2.计算直角三角形的数量
对于每一个位置(i,j)的1,我们计算它所在的行和列中1的数量。
如果grid[i][j]为1,则可以通过在同行中选择另一个1和在同列中选择另一个1来形成三角形。
这种情况下的三角形数量为(row_count - 1)*(col_count - 1),其中row_count是第i行中的1的数量,col_count 是第 j 列中的 1 的数量,减去当前的 1 是为了避免重复计算当前位置。
代码详解
#include <stdio.h>
#include <stdlib.h>
#include <string.h>//计算矩阵中的直角三角形数量
long long numberOfRightTriangles(int** grid, int gridSize, int* gridColSize) {int n = gridSize, m = gridColSize[0];int* col = (int*)malloc(m * sizeof(int));//动态分配内存用于计算计数数组memset(col, 0, m * sizeof(int));//将数组col中的所有数组初始化为0//计算每列中1的数量for (int i = 0; i < n; i++){for (int j = 0; j < m; j++) {col[j] += grid[i][j];}}long long res = 0;//用于存储直角三角形的数量for (int i = 0; i < n; i++){int row = 0;//计算当前行中1的数量for (int j = 0; j < m; j++){row += grid[i][j];}//对于当前行中的每个1,计算能够构成的直角三角形数量for (int j = 0; j < m; j++){if (grid[i][j] == 1) {//如果grid[i][j]为1,则可能构成三角形的个数为(row - 1) * (col[j] - 1)res += (long long)(row - 1) * (col[j] - 1);}}}free(col);//释放动态分配的内存return res;}
int main() {// 测试用例1int grid1Data[][3] = {{0, 1, 0},{0, 1, 1},{0, 1, 0}};int gridSize1 = 3;int gridColSize1 = 3;int** grid1 = (int**)malloc(gridSize1 * sizeof(int*));for (int i = 0; i < gridSize1; i++) {grid1[i] = (int*)malloc(gridColSize1 * sizeof(int));memcpy(grid1[i], grid1Data[i], gridColSize1 * sizeof(int));}int gridColSizes1[] = { gridColSize1, gridColSize1, gridColSize1 };printf("Output: %lld\n", numberOfRightTriangles(grid1, gridSize1, gridColSizes1));for (int i = 0; i < gridSize1; i++) {free(grid1[i]);}free(grid1);// 测试用例2int grid2Data[][4] = {{1, 0, 0, 0},{0, 1, 0, 1},{1, 0, 0, 0}};int gridSize2 = 3;int gridColSize2 = 4;int** grid2 = (int**)malloc(gridSize2 * sizeof(int*));for (int i = 0; i < gridSize2; i++) {grid2[i] = (int*)malloc(gridColSize2 * sizeof(int));memcpy(grid2[i], grid2Data[i], gridColSize2 * sizeof(int));}int gridColSizes2[] = { gridColSize2, gridColSize2, gridColSize2 };printf("Output: %lld\n", numberOfRightTriangles(grid2, gridSize2, gridColSizes2));for (int i = 0; i < gridSize2; i++) {free(grid2[i]);}free(grid2);// 测试用例3int grid3Data[][3] = {{1, 0, 1},{1, 0, 0},{1, 0, 0},{1, 0, 1},{1, 0, 0},{1, 0, 0}};int gridSize3 = 6;int gridColSize3 = 3;int** grid3 = (int**)malloc(gridSize3 * sizeof(int*));for (int i = 0; i < gridSize3; i++) {grid3[i] = (int*)malloc(gridColSize3 * sizeof(int));memcpy(grid3[i], grid3Data[i], gridColSize3 * sizeof(int));}int gridColSizes3[] = { gridColSize3, gridColSize3, gridColSize3, gridColSize3, gridColSize3, gridColSize3 };printf("Output: %lld\n", numberOfRightTriangles(grid3, gridSize3, gridColSizes3));for (int i = 0; i < gridSize3; i++) {free(grid3[i]);}free(grid3);return 0;
}相关文章:

力扣刷题之3128.直角三角形
题干描述 给你一个二维 boolean 矩阵 grid 。 请你返回使用 grid 中的 3 个元素可以构建的 直角三角形 数目,且满足 3 个元素值 都 为 1 。 注意: 如果 grid 中 3 个元素满足:一个元素与另一个元素在 同一行,同时与第三个元素…...

OD C卷 - 机场航班调度
机场航班调度(100) 航班组成:前两个大写字母代表航空公司缩写,后面4个数字代表航班信息;对输入的航班排序 首先按照航空公司缩写升序排序;同一航空公司的按照航班信息升序排序; 输入描述&…...

uni-app中使用支付宝扫码插件并且在真机调试时使用(详细教程)
前言:uni-app自带的扫码api 识别不灵敏,每次都得扫很长时间且不断调整才能扫出来码,所以决定使用支付宝扫码插件,官方插件地址:https://ext.dcloud.net.cn/plugin?id2636#detail 使用步骤: 1、下载插件到项目中 2、…...
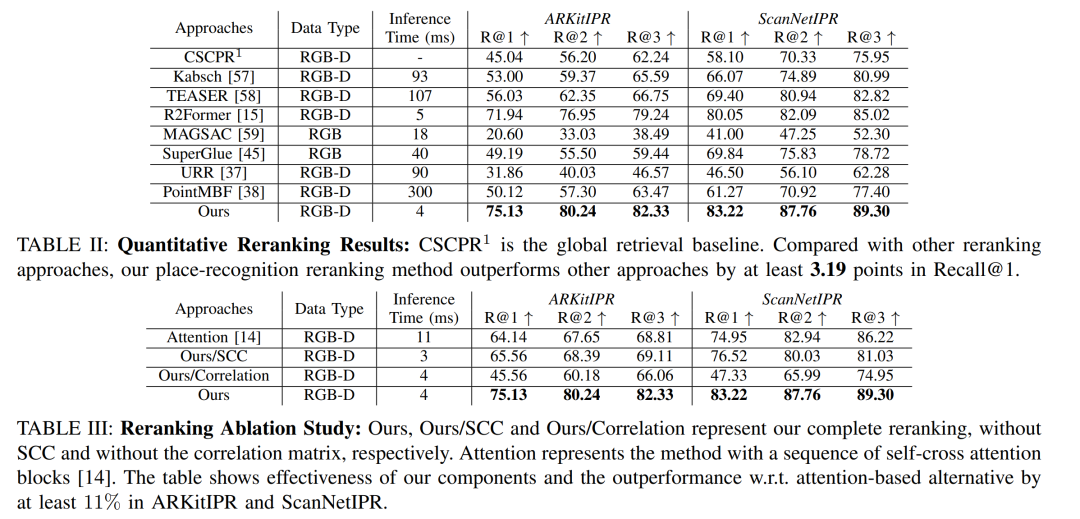
每日学术速递8.5—1
1.SV4D: Dynamic 3D Content Generation with Multi-Frame and Multi-View Consistency 标题: SV4D:具有多帧和多视图一致性的动态 3D 内容生成 作者:Yiming Xie, Chun-Han Yao, Vikram Voleti, Huaizu Jiang, Varun Jampani 文章链接&…...

1、操作系统相关概念
1、操作系统是计算机上的第一层软件,用于管理计算机硬件设备,提高他们的利用率和通吐量,并为用户和应用程序提供一个接口。不同操作系统目标不同,查询设备的操作系统,侧重人机交互性;武器控制操作系统&…...

【ModelSim】仿真问题记录
1、波形出不全: 1、甚至连clk波形都出不来 2、个别波形只有到仿真结束的时候才出现 解决办法: 1、添加波形需要是实例中的net 2、排查是否存在声明与示例的位宽不一致的信号 3、观察是否存在未初始化的变量寄存器 4、缩短整个仿真的步长 2、Instance列…...

如何提高深度学习中数据运行的稳定性
在深度学习中,模型的训练通常会受到随机性因素的影响,如参数初始化、数据加载顺序等。这会导致每次训练得到的结果有所不同。要减少这种不稳定性,可以采取以下措施: 1.固定随机种子 通过设置随机种子,可以使得每次训…...

【连续数组】python刷题记录
R3-前缀和专题 绝对要用字典记录 ben神,前缀和字典 class Solution:def findMaxLength(self, nums: List[int]) -> int:#前缀和字典,key为差值,value为坐标dict{0:-1}#当前1和0的差值counter0ret0for i,num in enumerate(nums):#多1+1if…...

JavaScript青少年简明教程:DOM和CSS简介
JavaScript青少年简明教程:DOM和CSS简介 DOM简介 DOM(Document Object Model)将文档表示为一个树形结构,其中每个节点都是一个对象,每个对象都有其自身的属性和方法。 通过对DOM的操作,开发者可以使用编…...

架构师知识梳理(一):计算机硬件
目录 计算机硬件组成 CPU CPU的组成 CPU的功能 校验码 奇偶校验 CRC CRC计算案例 指令 指令指行过程 指令系统 指令系统分类 指令流水线技术 流水线技术相关计算公式 存储 计算机存储系统设计 高速缓存Cache 缓存的局部性原理 地址映射 替换算法 关于命中…...

从根儿上学习spring 四 之run方法启动第一段
图1 由上图我们可以看到,我把run方法分成了5个小段,每小段使用红框圈了起来,这一篇我们先开始讲第一段。大家需要关注下行号,我讲的时候可能会使用行号对应具体某行代码。 图1-289-290行: 没啥好说的定义了两个变量&…...

智能闹钟如何判断用户已经醒了?
智能闹钟判断用户是否已经醒来的方式主要依赖于其内置的传感器和算法系统。以下是一些常见的判断方法: 一、传感器监测 体动传感器:智能闹钟通常配备有体动传感器,用于监测用户的身体运动。当用户从睡眠状态转变为清醒状态,并开始…...

【算法】动态规划解决背包问题
应用场景——01背包问题 有一个背包,背包的容量为 4,现有如下物品 要求 1.目标为装入背包的总价值最大,并且重量不超出 2.要求装入的物品不能重复 动态规划算法介绍 1.动态规划算法的核心是:将大问题划分为小问题进行解决&…...

day09 工作日报表
日期 30日07月2024年 任务安排 今天主要就是讲了security类工作的原理,然后就是让我们自己做项目 工作中的问题 今天做项目的时候发现有时候用postman测试返回20001,说错误见控制台,但是控制台一片祥和,于是就尝试用tr…...

C++学习之路(1)— 第一个HelloWorld程序
C学习之路(1)— 第一个HelloWorld程序 一、前言 C在C语言的基础上添加了对面向对象编程和泛型编程的支持,在 20世纪90年代便是最重要的编程语言之一,并在21世纪仍保持强劲势头。C继承了C语言高效、简洁、快速和可移植性的传统。 …...

python3 pyside6图形库学习笔记及实践(三)
目录 前言菜单栏相关控件使用QtDesigner快速构建菜单栏结构语法 上下文菜单概念为窗体添加上下文菜单为控件添加上下文菜单 折叠菜单资源的加载内置图标Rcc的使用创建资源文件加载资源文件 前言 本系列文章为b站PySide6教程以及官方文档的学习笔记 原视频传送门:【…...

03 库的操作
目录 创建查看修改删除备份和恢复查看连接情况 1. 创建 语法 CRATE DATABASE [IF NOT EXISTS] db_name [create_specification [, create_specification] …] create_specification: CHARACTER SET charset_name CPLLATE collation_name 说明: 大写的标识关键…...

嵌入式人工智能(44-基于树莓派4B的扩展板-LED按键数码管TM1638)
树莓派性能非常强悍,但是对于某些复杂的项目来说,会出现心有余而口不足的情况,为了解决这类问题,可以在树莓派上使用扩展板,我们介绍几款常见的扩展板,不仅可以扩展到树莓派,其他单片机或嵌入式…...

linux通过抓包工具tcpdump查看80端口访问量情况
方法: tcpdump -i ens32 -tn dst port 80 -c 10 | awk -F"." {print $1"."$2"."$3"."$4} | sort | uniq -c | sort -nr |head -n 10 #-i:指定端口 #-t:在输出的每一行不打印时间戳 #-nÿ…...

Mac 上安装和卸载 SDKMAN 及管理多个 JDK
前言 当电脑上有多个 JDK 环境的时候,切换管理比较麻烦,这时候可以使用 SDKMAN 来安装、管理 JDK。 一、安装 SDKMAN! 1. 安装前置条件 首先,确保已经安装了 curl 。如果没有,可以通过 Homebrew 来安装: brew inst…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
