代码随想录算法训练营第二十九天| 62.不同路径、63. 不同路径 II
写代码的第二十九天
继续动归!!!
62.不同路径
思路
解决问题1:dp[i][j]的的含义是什么?本题给的是一个二维的表,判断从左上角走到右下角有多少种路径,所以dp应该是二维数组,dp[i][j]代表的是从起始点开始走到i,j位置时的路径数量。
解决问题2:递推公式是什么?也就是dp[i][j]=?本题中只能向右向下走,所以(i,j)位置的值只能由其上方或者左侧的dp值决定也就是(i-1,j)和(i,j-1)两个位置的值决定。dp[i-1][j]代表(i,j)位置上方的路径数量,dp[i][j-1]代表 (i,j)位置左侧的路径数量,所以dp[i][j]=dp[i-1][j]+dp[i][j-1]。
解决问题3:dp数组如何初始化?最开始的想法就是只对初始位置进行初始化,但是我们根据递推公式可以看见,如果我们想要第i位的值就需要i-1位的值,如果i=1,那么就需要i=0时的值,也就是第一行的全部值,所以初始化第一行也就是i=0这一行的所有值,同理也需要初始化j=0这一行的全部值。dp[0][j] = 1,dp[i][0]=1,为什么初始化为1,是因为在第一行中他只能向下走,只有一条路径,同理第一列中只能向右走,只有一条路径,所以初始化为1.
解决问题4:如何确定遍历顺序?我们是从左上到右下的路径,所以从左到右从上到下进行遍历。
解决问题5:输出搭配数组。为了判断是否和题意一致,方便后续改错。
正确代码:这个题中对我难度最大的是dp数组的初始化,笑死没想过该怎么初始化。最后需要注意输出的是dp[m-1][n-1],因为下标是从0开始的。第一行第一列已经处理完了,所以下面的range范围都是从1开始的。
class Solution:def uniquePaths(self, m: int, n: int) -> int:dp = [[0 for _ in range(n)] for _ in range(m)]for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1for i in range(1,m):for j in range(1,n):dp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]
63. 不同路径 II
思路
这个题和上一个题的区别在于在这个m*n的矩阵中是有障碍物的,也就是说遇到了障碍要直接越过,根据已经给出了二维数组,不是0的就是障碍物;如果障碍在第一行,那么遇到了障碍物之后的点都不能走了,因为只能向右向下,右侧遇到障碍物了只能向下走在向右走,不能向上走,所以当第一行有障碍物的时候,后面所有的点不会再走过,同理,当第一列有障碍物的时候只能向右走在向下,也就是当前障碍物下面的点都不会再走过。
根据上面的分析可以知道,本题的代码和上面题的代码区别在于,初始化第一行和第一列的dp数组,遇到障碍之前的都是1,从障碍开始的值都是零。如果在内部发现了障碍,那么当前这个障碍的点dp[i][j]就不应该存储任何数值,此路不通,所以应该将dp[i][j]赋值为0.
正确代码:m代表行,n代表列!
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])dp = [[0 for _ in range(n)] for _ in range(m)]for i in range(m):if obstacleGrid[i][0] == 0:dp[i][0] = 1else:breakfor j in range(n):if obstacleGrid[0][j] == 0:dp[0][j] = 1else:breakfor i in range(1,m):for j in range(1,n):if obstacleGrid[i][j] == 1:dp[i][j] = 0else:dp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]
相关文章:

代码随想录算法训练营第二十九天| 62.不同路径、63. 不同路径 II
写代码的第二十九天 继续动归!!! 62.不同路径 思路 解决问题1:dp[i][j]的的含义是什么?本题给的是一个二维的表,判断从左上角走到右下角有多少种路径,所以dp应该是二维数组,dp[i]…...

Go+Redis零基础到用户管理系统API实战_20240730 课程笔记
概述 如果您没有Golang的基础,应该学习如下前置课程。 Golang零基础入门Golang面向对象编程Go Web 基础Go语言开发REST API接口_20240728Go语言操作MySQL开发用户管理系统API教程_20240729Redis零基础快速入门_20231227 基础不好的同学每节课的代码最好配合视频进…...
ScreenAgent:基于LVLM的计算机控制智能体
ScreenAgent : A Vision Language Model-driven Computer Control Agent 论文链接: https://arxiv.org/abs/2402.07945https://arxiv.org/abs/2402.07945IJCAI 2024 1.概述 大型语言模型(LLM),诸如ChatGPT与GPT-4,在自然语言处理领域(涵盖生成、理解及对话等任务)展现出…...

谷粒商城实战笔记-129-商城业务-商品上架-nested数据类型场景
文章目录 扁平化处理扁平化处理导致的检索问题 解决方案:使用 nested 结构 在es的数据类型中有一个nested类型,本讲将重点讨论这个类型。 扁平化处理 PUT my_index/doc/1 {"group" : "fans","user" : [{"first&quo…...
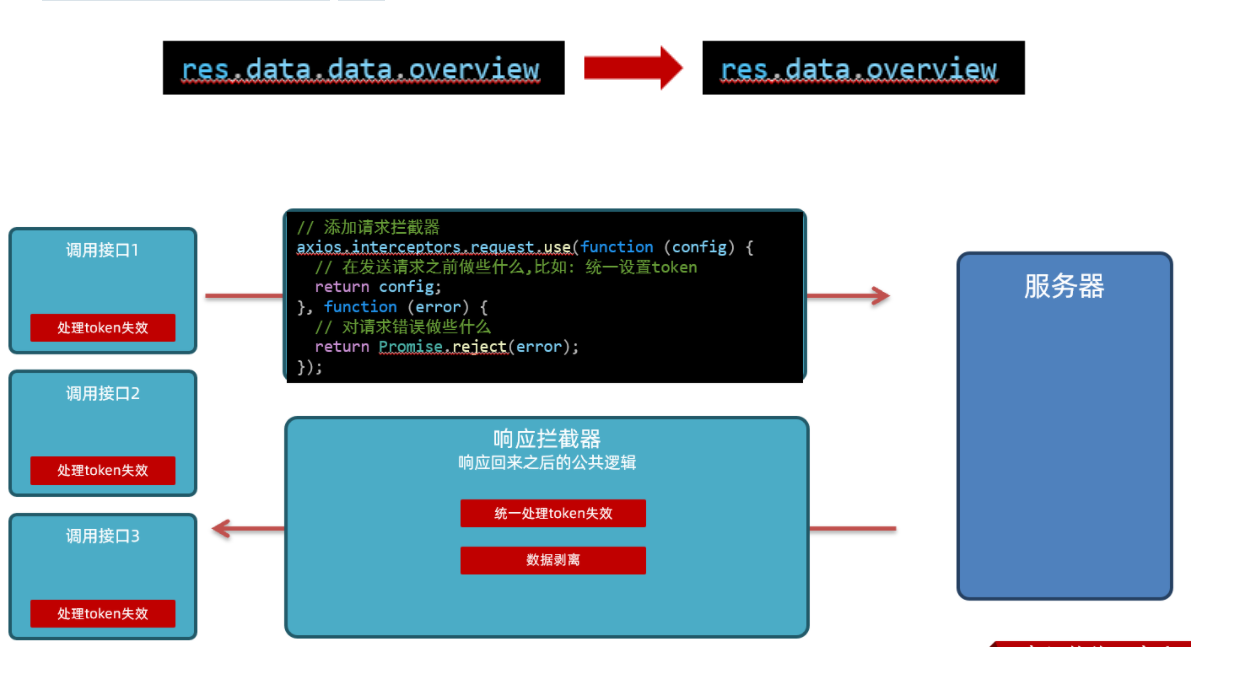
axios请求响应拦截器
目录 axios-拦截器 拦截器的作用 请求拦截器-基本写法: axios请求拦截器-统一设置token 需求: 核心步骤: 关键代码: 响应拦截器-基本写法: axios响应拦截器-统一处理token失效 需求: 核心步骤: 关键代码: axios响应拦截器-数据剥离 需求: 核心步骤: 关键代码: ax…...

Python 中单例模式实现的几种方式
在设计模式中,单例模式是经常被提及和使用的一种模式。它保证一个类只有一个实例,并提供全局访问点。在Python中,有多种实现单例模式的方法。那么,如何选择合适的方法来实现单例模式呢? 单例模式在Python中的几种实现方…...

mysql数据库触发器同步数据
首先检查数据源库是否支持触发器,show ENGINES,如果FEDERATED是NO,表示未开启,如需开启,再mysql配置文件中,添加federated配置到mysqld下面。 一、同服务器不同库触发器同步,这里只举例插入数据…...

Prometheus-v2.45.0+Grafana+邮件告警
目录 普罗米修斯监控架构介绍 Prometheus 监控架构 1. 数据抓取(Scraping) 2. 时序数据库(TSDB) 3. 数据模型 4. PromQL 查询语言 5. 告警(Alerting) 6. Alertmanager 7. 可视化(Visu…...

LeetCode——572. 另一颗树的子树
通过万岁!!! 题目:给你两棵树,然后问subRoot是不是root的子树。也就是root某个节点的所有孩子节点在值和结构上完全与subRoot相同。思路:我的思路比较简单,就是遍历root,遇到root中…...

Spring Boot整合MyBatis-Flex
说明:MyBatis-Flex(官网地址:https://mybatis-flex.com/),是一款数据访问层框架,可实现项目中对数据库的访问,类比MyBatis-Plus。本文介绍,在Spring Boot项目整合MyBatis-Flex。 创…...

重塑未来体验:边缘计算与云原生的完美邂逅
🐇明明跟你说过:个人主页 🏅个人专栏:《未来已来:云原生之旅》🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、云原生的兴起 2、边缘计算的兴起 二、边缘计算基础 …...

浅谈基础数论(c++)
目录 一些常见的符号表示阶乘定理 快速幂模板题代码扩展:矩阵快速幂主要作用 欧拉函数扩展积性函数 欧拉函数求法筛选法求欧拉函数(积性函数) 扩展欧几里得裴蜀定理问题分析代码 问题分析 同余与逆元如何求解逆元扩展欧几里得 例题讲解X-Magi…...

jdk 17新特性 sealed 关键字
通俗理解 sealed 关键字就是给对象继承加了权限控制一样,你必须在我的规则范围内才可以继承我的类 使用 permits 关键字控制允许哪些子类继承 子类必须加以下三个关键字: final 最终继承类(继承到这个类就不允许再往下继承了)n…...

在仪器计量校准中,无尘车间洁净室检测有哪些方法和流程?
仪器计量校准行业内,无尘车间洁净室检测可以说是较为热门的业务,因为其预算高,且检测流程不是太繁琐,很多仪器计量校准机构也是设立相关实验室,专门处理相关仪器的检测。不过虽然许多机构想要涉足该领域,但…...

【跨时代】第四次工业革命彻底来袭!什么是AI+
你有没有一种很割裂的感觉,就是在短视频里,AI已经要改变全世界了 但自己一用,却发现只能和AI聊聊天 画几张图 难道是姿势不对?但具体是哪里不对呢。 作为一个老牌程序员,我前面分享了很多计算机相关内容,总…...

前端性能优化-纲领篇
前端性能优化 本模块将梳理前端性能优化的相关知识点 从浏览器输入 URL 到页面展示发生了什么 完整版请查看[Browser_网络_安全]的部分,这里只是简单的梳理一下 DNS 解析TCP 连接浏览器发出 HTTP 请求服务器处理请求并返回 HTTP 报文浏览器解析渲染页面 性能优…...

深度学习-----------数值稳定性
目录 神经网络的梯度数值稳定性的常见两个问题例子:MLP 梯度爆炸梯度爆炸的问题 梯度消失梯度消失的问题 总结模型初始化和激活函数让训练更加稳定让每层的方差是一个常数 权重初始化正向均值和方差正向均值正向方差 反向均值和方差Xavier初始正向和反向的均值和方差…...

SpringBoot项目接口可以承受的调用次数
一个Spring Boot接口能够承受的调用次数主要取决于几个因素,包括但不限于: 服务器硬件:CPU、内存、硬盘I/O速度以及网络带宽都会直接影响接口的处理能力和并发量。操作系统和JVM配置:操作系统调度策略、JVM的内存分配、垃圾回收机…...
抽象代数精解【8】
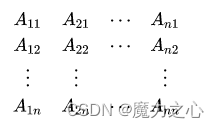
文章目录 希尔密码矩阵矩阵基本概念行列式基本概念特殊矩阵关于乘法运算构成群 加解密原理密钥加密函数解密函数 Z 26 上的运算( Z 256 与此类似) Z_{26}上的运算(Z_{256}与此类似) Z26上的运算(Z256与此类似&…...

数据结构与算法 - 二叉树
1. 概述 二叉树是这么一种树状结构:每个节点最多有两个孩子,左孩子和右孩子 完全二叉树:是一种二叉树结构,除了最后一层以外,每一层都必须填满,填充时要遵循从左到右 平衡二叉树:是一种二叉树…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
