世媒讯带您了解什么是媒体邀约
什么是媒体邀约?其实媒体邀约是一种公关策略,旨在通过邀请媒体记者和编辑参加特定的活动、发布会或其他重要事件,以确保这些活动能够得到广泛的报道和关注。通过这种方式,企业和组织希望能够传达重要信息,提高品牌知名度,并获得正面的公众舆论。下面我们来了解一下媒体邀约有哪些类型?

1.新闻发布会
通常是在有重大新闻或公告的时候举行,如新品发布、重要合作协议签署等。
通过媒体报道,迅速传播信息,增强公众影响力的目的。
2.媒体见面会
供一个与媒体面对面交流的机会,通常较为非正式,可以是午餐、晚宴等形式。
从而建立良好的媒体关系,促进未来更广泛和深入的报道。
3.活动邀约
邀请媒体参与品牌活动、产品体验会、展览、研讨会等。通过亲身体验让媒体更好地了解活动和品牌,从而帮助进行更为真实和生动的报道。
接下来我们需要了解如何进行有效的媒体邀约
1.精准定位
确定目标媒体和记者,了解其关注的领域和报道风格,确保邀请的对象和活动内容匹配。
2.提前计划
及早确定活动时间和地点,并提前数周发出邀请,方便媒体安排行程。
3.提供详细的活动信息
在邀请函中详细说明活动的目的、议程和亮点,必要时提供背景资料,帮助媒体更好地理解活动内容。
4.跟进确认
在活动前对接受邀请的媒体进行电话或邮件确认,以确保出席率。
5.准备媒体专用区
在活动现场设置专门的媒体区,提供便利的采访条件和工作环境,如Wi-Fi、充电站、饮品等。
6.个性化沟通
针对不同媒体和记者,提供个性化的沟通和服务,如一对一采访机会、独家内容等,以增强媒体体验。
媒体邀约的典型案例
第一个例如苹果公司每年都会举办盛大的新品发布会,吸引全球的科技媒体参与。通过这种方式,苹果的每次发布会和新品都能引起广泛的关注和报道,极大地提升了品牌的影响力。
第二个如特斯拉的汽车试驾活动,特斯拉会定期邀请汽车媒体和科技记者参与新车型的试驾活动,让媒体亲自体验其电动汽车的性能和特点。这不仅增加了媒体对特斯拉产品的了解,还创造了大量真实且有趣的报道内容。
媒体邀约是一个既传统又有效的公关手段,通过与媒体的深入互动和沟通,企业可以更好地传达其信息,建立品牌形象。世媒讯作为专业的媒体服务机构,能够帮助企业策划和执行高效的媒体邀约活动,帮助您实现公关目标。如果您想了解更多关于媒体邀约的信息或需要相关服务,请随时联系我们。
相关文章:

世媒讯带您了解什么是媒体邀约
什么是媒体邀约?其实媒体邀约是一种公关策略,旨在通过邀请媒体记者和编辑参加特定的活动、发布会或其他重要事件,以确保这些活动能够得到广泛的报道和关注。通过这种方式,企业和组织希望能够传达重要信息,提高品牌知名…...

[Kimi 笔记]“面向搜索引擎”
"面向搜索引擎"(Search Engine-Oriented,SEO-Oriented 或 SEO-Friendly)通常指的是在设计和开发网站时,采取一系列措施来优化网站内容和结构,以便提高网站在搜索引擎结果页面(SERP)中…...

如何在亚马逊云科技AWS上利用LoRA高效微调AI大模型减少预测偏差
简介: 小李哥将继续每天介绍一个基于亚马逊云科技AWS云计算平台的全球前沿AI技术解决方案,帮助大家快速了解国际上最热门的云计算平台亚马逊云科技AWS AI最佳实践,并应用到自己的日常工作里。 在机器学习和人工智能领域,生成偏差…...

订单定时状态处理业务(SpringTask)
文章目录 概要整体架构流程技术细节小结 概要 订单定时状态处理通常涉及到对订单状态进行定期检查,并根据订单的状态自动执行某些操作,比如关闭未支付的订单、自动确认收货等. 需求分析以及接口设计 需求分析 用户下单后可能存在的情况: …...

STM32 | ADC+RS485(第十天)
点击上方"蓝字"关注我们 01、ADC概述 ADC, Analog-to-Digital Converter的缩写,指模/数转换器或者模拟/数字转换器。是指将连续变量的模拟信号转换为离散的数字信号的器件。真实世界的模拟信号.例如温度、压力、声音或者图像等,需要转换成更容易储存、处理和发射的…...

python打包成能够在mac里面运行的程序
要将你的PyQt5应用程序打包成可以在macOS上运行的独立应用程序,可以使用工具如PyInstaller或py2app。下面是使用py2app的详细步骤,因为它是macOS上专用的打包工具,并且更好地支持PyQt5。 1. 安装py2app 首先,确保你的macOS系统上…...
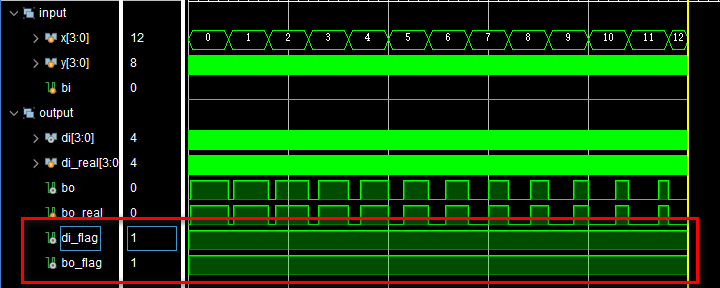
基于FPGA的数字信号处理(20)--半减器和全减器
目录 1、前言 2、半减器 3、全减器 4、减法器 文章总目录点这里:《基于FPGA的数字信号处理》专栏的导航与说明 1、前言 既然有半加器和全加器,那自然也有半减器和全减器了。尽管在电路中减法的实现基本都是 补码 加法 的形式,但是正所谓…...

Python:单引号,双引号,三引号的区别
在Python中,单引号()、双引号(")和三引号( 或 """)都可以用来定义字符串,但它们之间有一些区别: 单引号()和双引号…...

电子电气架构 ---SOMEIP/SD初入门
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

一些数学基础概念
一些数学基础概念 概率密度函数(PDF) 概率密度函数(Probability Density Function,简称 PDF)是描述连续随机变量的概率分布的一种函数。它用来表示随机变量在各个取值区间内的概率密度。 1. 定义 对于一个连续随机变量 ( X ),…...

责任有限公司的一般组织结构
责任有限公司(有限责任公司,LLC)的组织结构通常是为了确保公司运营的有效性和管理的透明度。以下是一般责任有限公司的组织结构及其主要组成部分: 1. 股东(Shareholders) 职责和角色 所有者:…...

Leetcode3227. 字符串元音游戏
Every day a Leetcode 题目来源:3227. 字符串元音游戏 解法1:博弈论 分类讨论: 如果 s 不包含任何元音,小红输。如果 s 包含奇数个元音,小红可以直接把整个 s 移除,小红赢。如果 s 包含正偶数个元音&am…...

网络流量分析在运维管理中的重要性与实施策略
在运维管理工作中,网络流量分析是一项不可或缺的技术手段。通过对网络流量的深入剖析,运维团队能够更全面地了解网络状态,及时发现潜在问题,优化网络性能,从而确保企业网络的稳定与高效运行。本文将详细探讨网络流量分…...

通信原理实验——PCM编译码
PCM编译码 实验目的 理解PCM编译码原理及PCM编译码性能熟悉PCM编译码专用集成芯片的功能和使用方法及各种时钟关系熟悉语音数字化技术的主要指标及测量方法 主要仪器设备及软件 硬件:多功能实验箱、示波器、导线 软件:无 实验原理 1. 抽样信号的量…...

matlab的strel()函数的使用方法(OK)
这个函数 是形态学的结构元素 使用方法如下 SE strel(nhood) SE strel("diamond",r) SE strel("disk",r) SE strel("disk",r,n) SE strel("octagon",r) SE strel("line",len,deg) SE strel("rectangle",…...

Linux:Linux权限解析
一、Linux下的用户分类 在Linux下,有两种用户,一种是超级用户,一种是普通用户 超级用户:可以再linux系统下做任何事情,不受权限限制(制定规则,但不需要遵守规则) 普通用户࿱…...
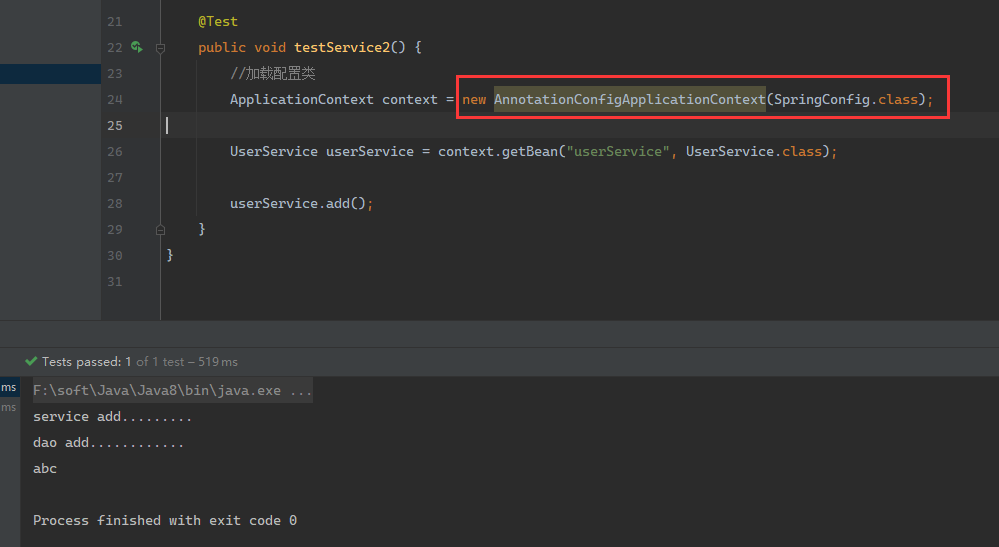
Spring面试篇章——IOC
IOC概念和原理 IOC概念 IOC就是控制反射,把对象创建和对象之间的调用过程,交给Spring进行管理使用IOC的目的:降低耦合度 IOC底层原理 xml解析、工厂模式、反射 图解: 原始模式 耦合度太高了,即当dao改了…...

适合制造业的项目管理软件都有哪些?
项目管理软件涉及进度、预算成本、资源、开发、流程、质量、风险、工时、知识文档、商务等各个方面,是企业项目管理领域的重要辅助工具,能够帮助组织提高项目管理水平与质量,确保项目顺利进行。 一、 奥博思 PowerProject 项目管理系统 Pow…...
、微前端(Micro Frontend)、Qiankun 框架之间的区别和联系)
微应用(Micro-Applications)、微前端(Micro Frontend)、Qiankun 框架之间的区别和联系
简简单单 Online zuozuo: 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo 简简单单 Online zuozuo :本心、输入输出、结果 简简单单 Online zuozuo :联系我们:VX :tja6288 / EMAIL: 347969164@qq.com 文章目录 微应用(Micro-Applications)、微…...

String的底层构造
1.String类对象的构造(后面有每一个接口的实现) #define _CRT_SECURE_NO_WARNINGS 1 #pragma once #include<iostream> #include<assert.h> using namespace std;namespace bit {class string{public:typedef char* iterator;typedef const…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
