力扣第五十三题——最大子数组和
内容介绍
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组
是数组中的一个连续部分。示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1] 输出:1示例 3:
输入:nums = [5,4,-1,7,8] 输出:23提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104进阶:如果你已经实现复杂度为
O(n)的解法,尝试使用更为精妙的 分治法 求解。
完整代码
int maxSubArray(int* nums, int numsSize) {int pre = 0, maxAns = nums[0];for (int i = 0; i < numsSize; i++) {pre = fmax(pre + nums[i], nums[i]);maxAns = fmax(maxAns, pre);}return maxAns;
}思路详解
一、问题背景
给定一个整数数组,要求找到数组中的最大子数组和。所谓最大子数组和,是指数组中一个或多个连续元素组成的子数组,其元素之和最大。
二、解题思路
-
动态规划:
- 使用动态规划的思想,通过遍历数组,记录当前位置之前所有可能的子数组和,从而找到最大的子数组和。
-
状态定义:
- 定义一个变量
pre来记录当前遍历到当前位置之前所有可能的子数组和的最大值。 - 初始时,
pre为0,因为第一个元素本身就是最大的子数组和。
- 定义一个变量
-
状态转移:
- 在遍历数组的过程中,对于每个元素,我们有两个选择:
- 将当前元素与之前的子数组和
pre相加,形成一个新的子数组和。 - 只考虑当前元素,形成一个新的子数组和。
- 将当前元素与之前的子数组和
- 我们选择这两个子数组和中的较大者作为新的
pre。
- 在遍历数组的过程中,对于每个元素,我们有两个选择:
-
结果记录:
- 在遍历过程中,我们需要记录
pre中的最大值,即当前找到的最大子数组和。 - 最终返回这个最大值。
- 在遍历过程中,我们需要记录
三、代码详解
- 初始化:
- 初始化
pre为0,表示当前还没有开始遍历数组。 - 初始化
maxAns为数组的第一个元素,因为至少包含一个元素的子数组和的最大值就是数组的第一个元素。
- 初始化
int pre = 0, maxAns = nums[0];
- 遍历数组:
- 遍历数组中的每个元素。
- 对于每个元素,计算两种情况下的子数组和,并取较大者作为新的
pre。 - 同时更新
maxAns为pre和maxAns中的较大者。
for (int i = 0; i < numsSize; i++) {pre = fmax(pre + nums[i], nums[i]);maxAns = fmax(maxAns, pre);
}
- 返回结果:
- 遍历结束后,
maxAns中存储的就是数组中的最大子数组和。 - 返回
maxAns。
- 遍历结束后,
return maxAns;
四、总结
通过动态规划的思想,我们能够高效地找到数组中的最大子数组和。关键在于维护当前遍历到当前位置之前所有可能的子数组和的最大值,并在遍历过程中不断更新这个值。这种方法的时间复杂度为O(n),空间复杂度为O(1),因为只需要常数级别的额外空间。
知识点精炼
一、核心概念
- 动态规划:一种通过保存中间结果来避免重复计算的算法设计技巧。
- 状态转移:在动态规划中,每个状态都是基于前一个状态计算得出的。
- 贪心算法:一种在每一步选择中都采取当前状态下最优(即看起来最有利)的选择,从而希望导致全局最优解的算法。
二、知识点精炼
-
最大子数组和问题:
- 要求在数组中找到一个子数组,其元素之和最大。
-
动态规划解法:
- 使用一个变量
pre来记录从数组开始到当前位置的所有可能的子数组和的最大值。 - 在遍历数组的过程中,更新
pre为当前元素与pre相加的和以及当前元素的较大者。
- 使用一个变量
-
状态转移:
- 在遍历数组的过程中,对于每个元素,有两种选择:
- 将当前元素与之前的子数组和
pre相加,形成一个新的子数组和。 - 只考虑当前元素,形成一个新的子数组和。
- 将当前元素与之前的子数组和
- 选择这两种子数组和中的较大者作为新的
pre。
- 在遍历数组的过程中,对于每个元素,有两种选择:
-
结果记录:
- 在遍历过程中,记录
pre中的最大值,即当前找到的最大子数组和。 - 最终返回这个最大值。
- 在遍历过程中,记录
三、性能分析
- 时间复杂度:O(n),因为需要遍历数组一次。
- 空间复杂度:O(1),只需要常数级别的额外空间。
四、实际应用
- 数据处理:在处理大量数据时,动态规划可以帮助我们找到最优解,从而提高效率。
- 算法竞赛:在算法竞赛中,掌握动态规划对于解决组合优化问题非常有帮助。
五、代码实现要点
- 初始化:正确初始化
pre和maxAns变量。 - 遍历数组:在遍历数组的过程中,正确更新
pre和maxAns变量。 - 返回结果:在遍历结束后,正确返回
maxAns变量。
动态规划的其他应用场景
-
最长公共子序列(LCS):
- 在两个或多个序列中找到最长的公共子序列,例如在文本编辑器中找到两个文本文件之间的差异。
-
最短路径问题:
- 在图论中,动态规划可以用于解决最短路径问题,例如Dijkstra算法和Floyd-Warshall算法。
-
背包问题:
- 在计算机科学中,背包问题是指给定一组物品和背包容量,如何选择物品放入背包以获得最大价值。
-
字符串匹配:
- 使用动态规划解决字符串匹配问题,如KMP算法,它可以高效地找到一个字符串在另一个字符串中出现的次数。
-
矩阵链乘法:
- 动态规划可以用来找到矩阵连乘的最优顺序,以最小化乘法运算的总次数。
-
最长递增子序列(LIS):
- 在数组中找到最长递增子序列的长度,例如在股票市场中找到最长的连续增长期。
-
编辑距离:
- 动态规划可以用来计算两个字符串之间的编辑距离,即通过插入、删除和替换字符来将一个字符串转换为另一个字符串的最少操作次数。
-
最优二叉搜索树:
- 动态规划可以用来构建最优二叉搜索树,即权值分配给节点,使得树的总权重最小。
-
股票买卖问题:
- 在股票市场中,动态规划可以用来解决如何在多次交易中最大化利润的问题。
-
硬币找零问题:
- 给定不同面值的硬币和需要找零的金额,动态规划可以用来找到找零的最少硬币数量。
相关文章:

力扣第五十三题——最大子数组和
内容介绍 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出&…...

达梦数据库:select报错:不是 GROUP BY 表达式
目录 SQL示例报错信息原因排查解决方法一:达梦支持灵活的处理方式,可以直接在查询中加hint参数方法二:修改dm.ini参数GROUP_OPT_FLAG1,动态,会话级参数,不用重启数据库方法三:配置兼容参数&…...

大模型卷向「下半场」,产业场景成拼杀重地
在19世纪的一个雨声潺潺的夏日,诗人拜伦与雪莱在瑞士的湖畔边闲聊,他们聊到了一个大胆的想法:如果能够把一个生物的各个部分制造出来,再组装到一起,赋予它生命的温暖,那会怎样? 这次对话激发了…...

OD C卷 - 多线段数据压缩
多段 线 数据压缩 (200) 如图中每个方格为一个像素(i,j),线的走向只能水平、垂直、倾斜45度;图中线段表示为(2, 8)、(3,7)、(3, 6)、(…...

密码学基础:搞懂Hash函数SHA1、SHA-2、SHA3(2)
目录 1.引入 2. SHA512-224\256 3.SHA-3 4.MD5 5.SM3 1.引入 上篇密码学基础:搞懂Hash函数SHA1、SHA-2、SHA3(1)-CSDN博客,我们先就将基础的SHA1\2讲解了,接下来我们继续聊SHA-3、SHA2变体SHA512_224\256等 2. SHA512-224\256 SHA512…...

C++ 异步编程:std::async、std::future、std::packaged_task 和 std::promise
C 异步编程:std::async、std::future、std::packaged_task 和 std::promise 在现代 C 编程中,异步编程已经成为一种常见的模式。利用 C11 引入的标准库组件 std::async、std::future、std::packaged_task 和 std::promise,我们可以更方便地处…...

OD C卷 - 石头剪刀布游戏
石头剪刀布游戏 (100) 剪刀石头布游戏,A-石头、B-剪刀、C-布游戏规则: 胜负规则,A>B; B>C; C>A;当本场次中有且仅有一种出拳形状优于其他出拳形状,则该形状的玩家是胜利者,否则认为是…...

关于k8s集群中kubectl的陈述式资源管理
1、k8s集群资源管理方式分类 (1)陈述式资源管理方式:增删查比较方便,但是改非常不方便 使用一条kubectl命令和参数选项来实现资源对象管理操作 (2)声明式资源管理方式:yaml文件管理 使用yam…...

XML 学习笔记
简介: (1)XML:可扩展性标记语言,用于传输和存储数据,而不是展示数据,是W3C 推举的数据传输格式。 XML的标签必须自定义,但是在写标签名的时候一定要有含义。 XML 只能有一个根节点…...
MongoDB未授权访问漏洞
2.MongoDB未授权访问漏洞 mongodb数据库是由C编写,主要是为了提供web应可用扩展的一种高性能数据库。开启MongoDB服务时不添加任何参数时,默认是没有权限验证的,登录的用户可以通过默认端口无需密码对数据库任意操作(增、删、改、查高危动作)而且可以远程访问数据库…...
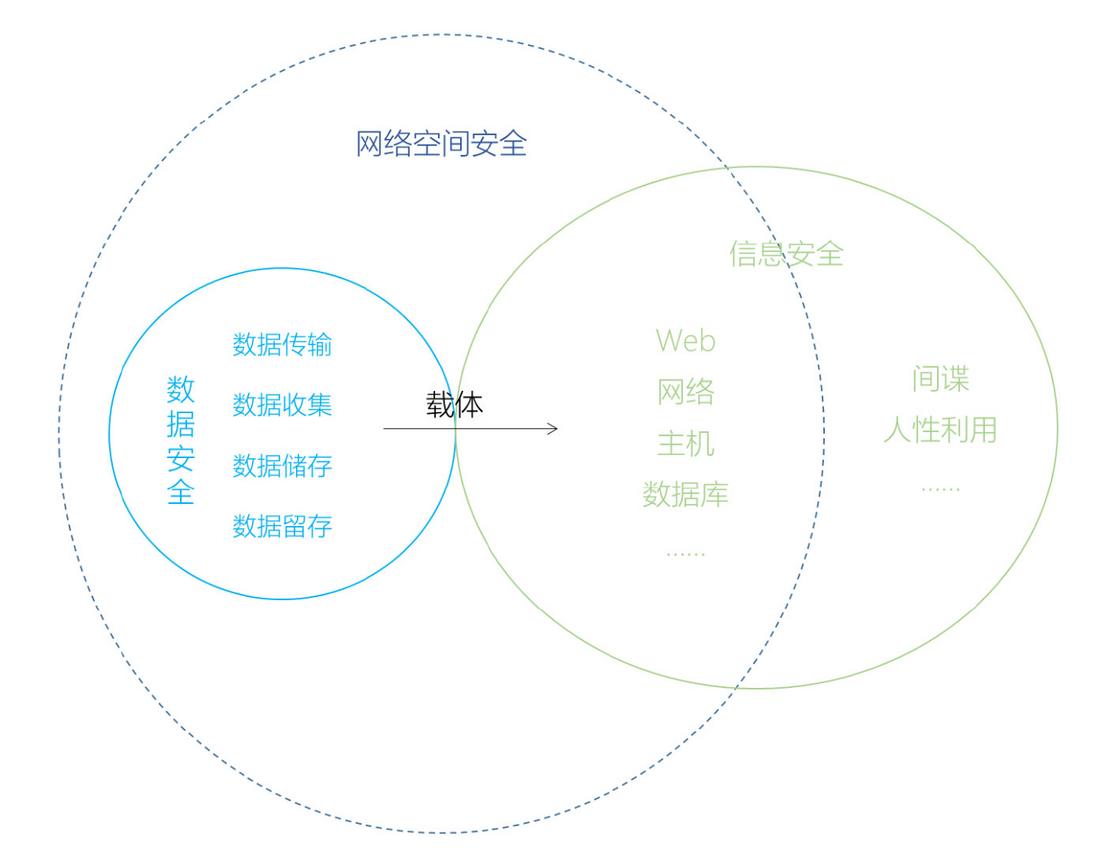
数据安全、信息安全、网络安全区别与联系
关键字: 信息安全 数据安全 网络安全 [导读] 让人更好理解 “数据安全”、“信息安全”、“网络安全” 三者间的区别与联系了,我们汇总了官方机构给这三者的定义,并且网友也给出了自己的看法,一起来看看。 在 “互联网 ” 被广…...

Jenkins未授权访问漏洞 *
漏洞复现 步骤一:使用以下fofa语法进行产品搜索.... port"8080" && app"JENKINS" && title"Dashboard [Jenkins]" 步骤二:在打开的URL中...点击Manage Jenkins --> Scritp Console在执行以下命令..…...

【爬虫原理】
《爬虫》 1、爬虫的概念 概念:(spider,网络蜘蛛)通过互联网上一个个的网络节点,进行数据的提取、整合以及存储 分类: 通用爬虫(了解) 主要用于搜索引擎(百度、…...

计算机组成原理 —— 指令流水线的基本概念
计算机组成原理 —— 指令流水线的基本概念 串行执行(Serial Execution)串行执行的特点串行执行的局限性串行执行的应用场景 并行执行定义基本原理五段式指令流水线优点缺点 流水线的性能指标示例计算 我们来了解一下指令流水线: 首先在这之…...

Python爬虫技术 第31节 持续集成和自动化部署
持续集成和自动化部署 Git版本控制 Git 是一个非常流行的分布式版本控制系统,用于跟踪对项目文件的修改。对于爬虫项目来说,使用Git可以帮助你管理代码的不同版本,协同开发,并且可以在出现问题时回滚到之前的版本。 基本操作&a…...
(第2版)课后习题答案)
数据结构(C语言版)(第2版)课后习题答案
数据结构(C语言版)(第2版)课后习题答案 李冬梅 2015.3 目 录 第 1 章 绪论 1 第 2 章 线性表 5 第 3 章 栈和队列 13 第 4 章 串、数组和广义表 26 第 5 章 树和二叉树 33 第 6 章 图 43 第 7 章 查找 54 第 8 章 排序 65…...
的分析总结及进一步提问)
打开轮盘锁问题(LeetCode)的分析总结及进一步提问
打开轮盘锁问题分析总结,及进一步提问:请给出一组最小步数下的号码序列组合 题目描述 你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由…...

python——joblib进行缓存记忆化-对计算结果缓存
问题场景 在前端多选框需要选取多个数据进行后端计算。 传入后端是多个数据包的对应路径。 这些数据包需要按一定顺序运行,通过一个Bag(path).get_start_time() 可以获得一个float时间值进行排序,但由于数据包的特性,这一操作很占用性能和时…...

Linux文件管理
系列文章目录 提示:仅用于个人学习,进行查漏补缺。 1.Linux介绍、目录结构、文件基本属性、Shell 2.Linux常用命令 3.Linux文件管理 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1…...

《Unity3D网络游戏实战》学习与实践--制作一款大乱斗游戏
角色类 基类Base Human是基础的角色类,它处理“操控角色”和“同步角色”的一些共有功能;CtrlHuman类代表“操控角色”,它在BaseHuman类的基础上处理鼠标操控功能;SyncHuman类是“同步角色”类,它也继承自BaseHuman&…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
