P10289 [GESP样题 八级] 小杨的旅游
Description
给定一棵 n n n 个点的树,每条边权值均为 1 1 1,树上有 k k k 个关键点,关键点们在 0 0 0 的时间内相互可达, q q q 次询问,求 s → t s\to t s→t 的最短路。
Analysis
考虑暴力建图,则图上共有 ( n − 1 + n ( n − 1 ) 2 ) (n-1+\frac{n(n-1)}{2}) (n−1+2n(n−1))条边,在 n , k n,k n,k 均为最大的情况下,图上共有大约 2 × 1 0 10 2 \times 10^{10} 2×1010 条边,铁定 MLE。
我们注意到,从 s s s 到 t t t 只有两种情况:
- 老老实实从树上走;
- 从 s s s 走到一个关键点 k 1 k_1 k1,穿越到另一个关键点 k 2 k_2 k2,再走到 t t t。
第一种情况就是常规树上两点最短路。
第二种情况,根据贪心思想,选取的 k 1 , k 2 k_1,k_2 k1,k2 一定是距离 s , t s,t s,t 最近的两个。所以我们初始时一次 bfs 求出每个点 i i i 到传送门的距离 d s t i dst_i dsti,最终答案即为 d s t s + d s t t dst_s+dst_t dsts+dstt。
Code
// Problem: P10289 [GESP样题 八级] 小杨的旅游
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P10289
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <iostream>
#include <queue>
#include <cmath>
using namespace std;using Graph = vector<vector<int>>;
const int INF = 1e9;struct LCA{int n, k;vector<int> dep;vector<vector<int>> f;Graph G;LCA() {}LCA(const Graph &tree): G(tree){n = G.size();k = (int)log2(n) + 1;dep.assign(n, 0);f.assign(n, vector<int>(k, -1));dfs(0, 0);}void dfs(int u, int fa){dep[u] = dep[fa] + 1;f[u][0] = fa;for(int i = 1; i < k; i++) f[u][i] = f[f[u][i - 1]][i - 1];for(auto v: G[u]){if(v == fa) continue;dfs(v, u);}}int lca(int x, int y){if(dep[x] < dep[y]) swap(x, y);for(int i = k - 1; i >= 0; i--)if(dep[f[x][i]] >= dep[y]) x = f[x][i];if(x == y) return x;for(int i = k - 1; i >= 0; i --)if(f[x][i] != f[y][i]){x = f[x][i];y = f[y][i];}return f[x][0];}int dist(int x, int y){return dep[x] + dep[y] - 2 * dep[lca(x, y)];}};signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int n, k, q;cin >> n >> k >> q;Graph G(n);for (int i = 0, u, v; i < n - 1; i++) {cin >> u >> v;u--, v--;G[u].push_back(v);G[v].push_back(u);}LCA tree(G);queue<int> que;vector<int> dis(n, INF);for (int i = 0, x; i < k; i++) {cin >> x;x--;que.push(x);dis[x] = 0;}while (que.size()) {int u = que.front();que.pop();for (auto v: G[u])if (dis[v] == INF) {dis[v] = dis[u] + 1;que.push(v);}}auto dist = [&](int x, int y) {return min(tree.dist(x, y), dis[x] + dis[y]);};for (int i = 0, u, v; i < q; i++) {cin >> u >> v;u--, v--;cout << dist(u, v) << endl;}return 0;
}
相关文章:

P10289 [GESP样题 八级] 小杨的旅游
Description 给定一棵 n n n 个点的树,每条边权值均为 1 1 1,树上有 k k k 个关键点,关键点们在 0 0 0 的时间内相互可达, q q q 次询问,求 s → t s\to t s→t 的最短路。 Analysis 考虑暴力建图,…...

网络编程 ----------- 4、组播与广播
1、广播 broadcast 广播是指向同一个网络中所有的主机传输数据只有传输层协议为 UDP协议时,才支持广播 TCP是端对端,广播是一对多 ,所以无法符合其要求。 1)广播地址 广播地址的计算: 子网掩码…...

最短路径算法:Bellman-Ford算法
引言 在图论中,Bellman-Ford算法是一种用于计算单源最短路径的算法。与Dijkstra算法不同,Bellman-Ford算法可以处理带有负权边的图,并且可以检测图中是否存在负权环。本文将详细介绍Bellman-Ford算法的定义、步骤及其实现。 Bellman-Ford算…...

爬虫:xpath模块及昵图网实例
xpath模块 from lxml import etreestr1 """ <div><ul><li class"item-0"><a href"link1.html">first item</a></li><li class"item-1"><a href"link2.html">second…...

高级java每日一道面试题-2024年8月03日-web篇-forward和redirect有什么区别?
如果有遗漏,评论区告诉我进行补充 面试官: forward和redirect有什么区别? 我回答: 在Java Web开发中,forward和redirect是Servlet容器提供的两种用于页面跳转的技术。它们的主要区别在于客户端感知的方式、URL地址的变化、请求对象的共享等方面。下面详细介绍两…...

如何让你的网站拥有更好的体验
在HTML中,属性是用于提供关于HTML元素的额外信息。接下来我们将讲解13个可以让用户拥有更好体验的HTML属性。 Accept 属性 我们可以在<input>元素(仅适用于文件类型)中使用accept属性来指定服务器可以接受的文件类型。 <input ty…...

opencascade AIS_TypeFilter AIS_XRTrackedDevice源码学习
opencascade AIS_TypeFilter 前言 通过它们的类型选择交互对象。该过滤器会对本地上下文中的每个交互对象提出问题, 以确定它是否具有非空的所有者,并且如果是,则检查它是否是所需类型。 如果对象在每种情况下都返回 true,则保留…...

使用Spring AOP监控指定方法执行时间
文章目录 一、加入pom依赖二、切面类和注解三、执行方法 一、加入pom依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId></dependency>二、切面类和注解 import java.lang.…...

最新CSS3纵向菜单的实现
纵向菜单 通过下面例子,你会知道把列表转换成菜单的关键技术 a中的#是URL的占位符可以点击,真正用途中写实际URL <nav class"list1"><ul><li><a href"#">Alternative</a></li><li><…...

GooLeNet模型搭建
一、model import torch from torch import nn from torchsummary import summaryclass Inception(nn.Module):def __init__(self, in_channels, c1, c2 , c3 , c4):super(Inception, self).__init__()self.ReLU nn.ReLU()#路线1:1x1卷积self.p1_1 nn.Conv2d(in_channels i…...

使用ThreadLocal来存取单线程内的数据
一.什么是ThreadLocal? ThreadLocal,即线程本地变量。如果你创建了一个 ThreadLocal变量,那么访问这个变量的每个线程都会有这个变量的一个本地拷贝,多个线程操作这个变量的时候,实际是在操作自己本地内存里面的变量&…...
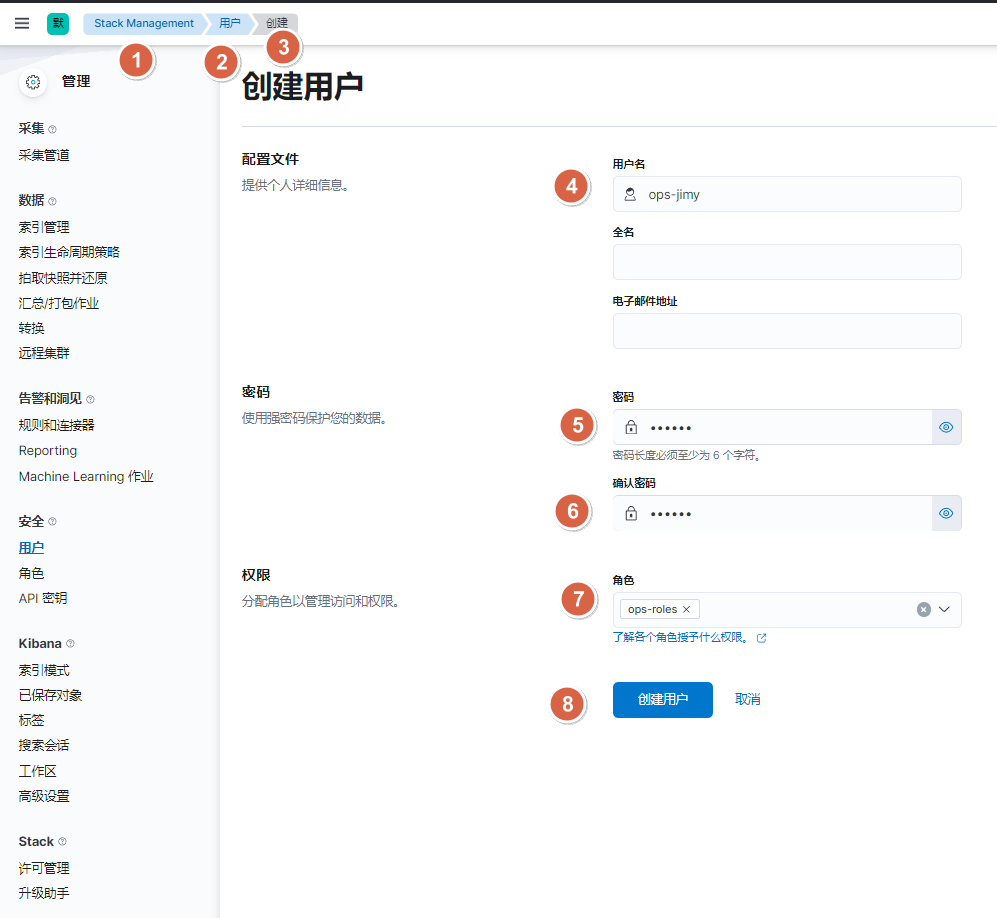
elasticsearch教程
1. 单点部署(rpm): #提前关闭firewalld,否则无法组建集群 #1. 下载ES rpm包 ]# https://www.elastic.co/cn/downloads #2. 安装es ]# rpm -ivh elasticsearch-7.17.5-x86_64.rpm #3. 调整内核参数(太低的话es会启动报错) echo "vm.max_map_count655360 fs.file-max 655…...

Arrays、Lambda表达式、Collection集合
1. Arrays 1.1 操作数组的工具类 方法名说明public static String toString(数组)把数组拼接成一个字符串public static int binarySearch(数组,查找的元素)二分查找法查找元素public static int[] copyOf(原数组,新数组长度)拷贝数组public static int[] copyOfRange(原数组…...

2024年前端趋势:全栈或许是不容错过的选择!
近年来,前端开发的技术不断推陈出新,2024年也不例外。在这个变化迅速的领域,全栈开发逐渐成为一股不容忽视的趋势。无论你是经验丰富的开发者,还是刚刚入门的新手,掌握全栈技术都能让你在竞争中脱颖而出。而在这个过程…...
MySQL 实战 45 讲(01-05)
本文为笔者学习林晓斌老师《MySQL 实战 45 讲》课程的学习笔记,并进行了一定的知识扩充。 sql 查询语句的执行流程 大体来说,MySQL 可以分为 Server 层和存储引擎层两部分。 Server 层包括连接器、查询缓存、分析器、优化器和执行器。 连接器负责接收客…...

仓颉编程语言入门 -- Array数组详解
仓颉编程语言入门 – Array数组详解 一. 如何创建Array数组 我们可以使用 Array 类型来构造单一元素类型,有序序列的数据。 1.仓颉使用 Array 来表示 Array 类型。T 表示 Array 的元素类型,T 可以是任意类型 , 类似于泛型的概念 var arr:Array<St…...

C#初级——简单单例模式使用
单例模式 单例模式是一种常用的软件设计模式,它确保一个类只有一个实例,并提供一个全局访问点来获取这个实例,通过单例模式防止私有成员被多次引用,防止数据被随意纂改。本文使用的是线程不安全的懒汉式单例。 创建单例模式 首…...

2024.07.29 校招 实习 内推 面经
地/球🌍 : neituijunsir 交* 流*裙 ,内推/实习/校招汇总表格 1、校招 | 美/团// 快驴、小象、优/选/事/业/部2024年校/园/招聘(内推) 校招 | 美团快驴、小象、优选事业部2024年校园招聘(内推ÿ…...

速盾:爬虫攻击和cc攻击的区别是什么?
爬虫攻击和CC(Distributed Denial of Service)攻击是网络安全领域两种不同类型的攻击方式。尽管它们都涉及对目标网站或服务器的非法访问,但它们的目的、方法和影响各不相同。在接下来的文章中,我们将详细介绍这两种攻击方式的区别…...

Tomcat与Nginx的区别详解
目录 引言Tomcat概述 Tomcat的历史Tomcat的架构Tomcat的功能Nginx概述 Nginx的历史Nginx的架构Nginx的功能Tomcat与Nginx的区别 架构上的区别...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
