系统化学习 H264视频编码(06)哥伦布编码
说明:我们参考黄金圈学习法(什么是黄金圈法则?->模型 黄金圈法则,本文使用:why-what)来学习音H264视频编码。本系列文章侧重于理解视频编码的知识体系和实践方法,理论方面会更多地讲清楚 音视频中概念的起源以及各个概念的联系。知其然,知其所以然。同时更强调知识系统的建立。
针对本文,我们主要研究上一篇文章(系统化学习 H264视频编码(05)码流数据及相关概念解读)中提到的 H.264码流中的数据编码,也就是哥伦布编码。解读为什么要使用哥伦布编码以及哥伦布编码到底是怎么计算的。
1 为什么H264编码中使用哥伦布编码来编码来压缩数据?
我们将其拆分成2个问题:为什么H264编码中使用熵编码来压缩数据,以及为什么使用熵编码中的哥伦布编码来编码。
1.1 为什么H264编码中使用熵编码来压缩数据?
在视频编码中,熵编码方法被广泛使用,主要是因为它能够有效地减少数据的冗余,从而提高压缩效率。以下是使用熵编码方法的几个关键原因:
-
信息熵的概念: 信息熵是度量信息的不确定性的量。熵编码方法的核心思想是为更可能发生的事件分配更短的编码,从而最小化总体编码长度,接近信息熵的理论极限。
-
利用数据的统计特性: 视频数据具有明显的统计规律性,例如在自然场景中相邻像素之间存在很强的相关性。熵编码利用这些统计特性,通过为高频事件分配短码字,为低频事件分配长码字,实现数据的有效压缩。
-
无损压缩: 熵编码是一种无损压缩方法,这意味着原始视频数据可以从压缩后的数据完全恢复,不损失任何信息。
-
适应性: 熵编码可以适应各种不同的数据源和不同的编码场景。它可以动态地根据数据的实际分布调整编码策略。
-
减少存储和传输成本: 通过减少视频数据的大小,熵编码可以显著降低存储成本和网络带宽需求,这对于视频的存储和传输尤为重要。
-
提高编码效率: 熵编码通常作为视频编码流程的最后一步,对已经通过变换和量化处理过的数据进行进一步压缩,从而提高整体编码效率。
-
兼容性和标准化: 熵编码方法如哈夫曼编码、算术编码等已经被广泛地集成到视频编码标准中,如H.264、H.265、VP9等,这些标准确保了不同编码器和解码器之间的兼容性。
-
优化编码性能: 熵编码可以与其他视频编码技术(如帧内预测、帧间预测、变换和量化)相结合,共同优化编码性能。
-
灵活性和扩展性: 熵编码方法可以根据新的压缩需求和技术进步进行调整和扩展,以实现更高的压缩效率。
-
减少计算复杂度: 相比其他一些压缩技术,熵编码方法通常具有较低的计算复杂度,这使得它适合于实时视频编码和解码应用。
综上所述,熵编码方法在视频编码中的应用可以显著提高压缩效率,降低存储和传输成本,同时保持数据的无损性,这些优势使其成为视频编码中不可或缺的一部分。
1.2 那么多熵编码算法,为什么选择哥伦布编码?
哥伦布编码(Golomb coding)是一种熵编码方法,它与一些其他类型的编码方法有相似之处,尤其是在它们都是变长编码(Variable-Length Coding, VLC)这一点上。但是同类型的编码算法那么多,为什么视频编码中选择使用哥伦布编码而不是其他编码算法呢?
主要是因为哥伦布编码具有以下几个关键优势:
- 与信源无关:哥伦布编码的编码规则与信源的概率分布无关,这意味着它适用于各种类型的数据流,而不需要针对特定信源调整编码规则。
- 无需额外信息:使用哥伦布编码时,不需要携带额外的码表信息,这简化了编码过程并减少了必要的数据传输量。
- 压缩效率:尽管哥伦布编码的压缩率可能不如霍夫曼编码等算法,但在实际的视频编码应用中,它提供了足够的压缩效率,同时保持了较低的计算复杂度。
- 编码复杂度低:与霍夫曼编码相比,哥伦布编码的运算复杂度较低,这使得它更适合于需要处理大量数据的视频编码场景。
- 适应性:哥伦布编码能够适应视频数据中的不同统计特性,尤其是在编码变换系数时,可以有效地处理视频数据中的稀疏性。
- 容错性:哥伦布编码的结构有助于在不完美或有噪声的传输环境中保持较好的容错性,这对于视频流的稳定性至关重要。
- 广泛应用于视频编码标准:哥伦布编码被广泛应用于多个视频编码标准中,如H.264,这表明它在实际应用中已被证明是有效的。
- 易于实现:哥伦布编码的实现相对简单,易于在硬件和软件中部署,这对于降低编解码器的开发和维护成本非常重要。
综上所述,哥伦布编码因其简单性、适应性、以及在视频编码中的高效性,成为视频编码领域中一个受欢迎的选择。
2 什么是哥伦布编码?
视频编码中的哥伦布编码是一种用于压缩数据的熵编码技术,它特别适合于编码那些具有几何分布特性的数值,比如在视频编码中常见的变换系数。哥伦布编码能够有效地表示这种类型的数据,因为它可以为频繁出现的较小数值分配较短的编码,而不常见的较大数值则分配较长的编码。
哥伦布编码的基本思想是将每个待编码的非负整数转换为一个较短的二进制表示形式。这种转换基于一个简单的观察:在许多自然信号中,较小的数值出现的频率远高于较大的数值。
2.1 形象解读哥伦布编码
想象一下,你管理着一个巨大的图书馆,这个图书馆的书籍数量非常庞大,而且种类繁多。每本书都有一个唯一的编码,用于标识和检索。在这个图书馆中,有些书籍非常受欢迎,借阅的频率很高(相当于小数值),而有些书籍则很少被人问津(相当于大数值)。为了简化编码系统并节省空间,你决定使用一种特殊的编码规则,这就是类似于哥伦布编码的系统:
- 编号调整:首先,你决定对每本书的编号进行加1处理,因为图书馆中没有编号为0的书。
- 二进制转换:接着,你将每本书的编号转换为二进制形式。
- 寻找最长的0前缀:在二进制编号中,你从最高位开始寻找第一个1的位置,1前面的所有0构成了一个序列。
- 编码生成:在找到的1前面,你添加相同数量的0,然后紧跟着是1后面所有的二进制位,这样就形成了这本书的哥伦布编码。
- 编码优势:这种编码方式的好处在于,那些编号较小(即受欢迎的)书籍的编码会很短,因为它们的二进制表示中1出现得很快,不需要太多0前缀。而不那么受欢迎的书籍,虽然编号较大,但它们的编码也不会太长,因为它们本来就不常被借阅。
- 解码过程:当需要找到一本书时,你从编码的第一个位开始向左数,直到遇到第一个1,然后根据1前面的0的数量确定书籍的编号,从而快速检索到书籍。
通过这个比喻,我们可以看到哥伦布编码如何为不同频率出现的数值提供一种高效的编码方式,这与图书馆中根据书籍的受欢迎程度来优化编码和检索系统非常相似。
2.2 0阶无符号指数哥伦布编码
正常来说,哥伦布编码可以拓展位k阶,但是在H264中使用的是0阶指数哥伦布编码,在H.264中使用ue(v)表示0阶无符号指数哥伦布编码的解码过程,用se(v)表示0阶有符号指数哥伦布编码过程。0阶无符号指数哥伦布编码最后生成的比特串格式为"前缀1后缀",前缀和后缀的长度是相同的。假如待编码数字codeNum = 5,0阶无符号指数哥伦布编码的步骤如下:
- 将数字5以二进制写出,5的二进制为101,因为0阶指数哥伦布编码,所以不用去掉低位。
- 将上面的二进制+1,101加1为110,留下的比特数为3,3-1=2,所有需要增加前导0的个数为2
- 因为第一步没有去掉,所有这一步不进行任何操作,最终生成的比特串为00110
通过这种方式,哥伦布编码能够为视频编码中的变换系数提供一种高效的编码方式,从而减少视频数据的总体大小,实现高效视频压缩。下面是对其他不同codeNum进行编码的结果,如下所示:

最后,总结下哥伦布编码的具体步骤:
-
加1操作:首先,将待编码的数值加1。这是因为哥伦布编码需要处理非负整数,而0作为一个特殊值,通过加1操作可以避免在编码中单独处理。
-
二进制表示:将加1后的数值转换为二进制形式。
-
寻找最长的0前缀:在二进制表示中,从最高位(最左边)开始数,找到第一个1的位置,1前面所有的0就构成了最长的0前缀。
-
编码生成:在1的前面添加与0前缀长度相等的0,然后在1后面放置原始二进制表示中1后面的所有位,这样就形成了哥伦布编码。
-
解码过程:解码时,从编码的第一位开始向左数,直到遇到第一个1,1前面的0的数量就是编码的长度。然后根据这个长度,从1后面读取相应数量的位,还原为原始数值。
2.3 扩展知识:k阶无符号指数哥伦布编码
k阶无符号指数哥伦布编码步骤如下所示:
(1)将codeNum加上2^k,k-0时是1;k=1时是2;k=2时是4;
(2)将codeNum加上2^k的数字用二进制表示;
(3)计算二进制长度len,然后在其前面加上前缀 len-1-k个0;
比特串的格式位"前缀1后缀"。前缀 = 后缀 - k,下面是对其他不同codeNum进行k阶无符号指数哥伦布编码的结果,如下所示:

相关文章:

系统化学习 H264视频编码(06)哥伦布编码
说明:我们参考黄金圈学习法(什么是黄金圈法则?->模型 黄金圈法则,本文使用:why-what)来学习音H264视频编码。本系列文章侧重于理解视频编码的知识体系和实践方法,理论方面会更多地讲清楚 音视频中概念的…...

手机在网状态接口如何对接?(一)
一、什么是手机在网状态? 传入手机号码,查询该手机号的在网状态,返回内容有正常使用、停机、在网但不可用、不在网(销号/未启用/异常)、预销户等多种状态。 二、手机在网状态使用场景? 1.信贷审核&#…...

数据结构链表2(常考习题1)(C语言)
移除链表元素: . - 力扣(LeetCode) 题目: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 解题思路: 情况1: 情…...

Rust的运行时多态
Rust的运行时多态 Rust的静态多态即编译时多态,通过**泛型特征约束(Generic Type Trait Constrait)**来实现; 那么动态多态(运行时多态)呢?答案是特征对象(Trait Objectÿ…...

sqllabs通关
sqllabs5:(报错注入) ?id1 回显You are in........... ?id2-1 回显You are in........... ?id1 回显 1 LIMIT 0,1 判断是字符型,闭合。?id1order by 3-- //页面显示正常我们试了4行得出是报错注入 我们先爆库名 http://127.0.0.1/sqli-labs-master/L…...
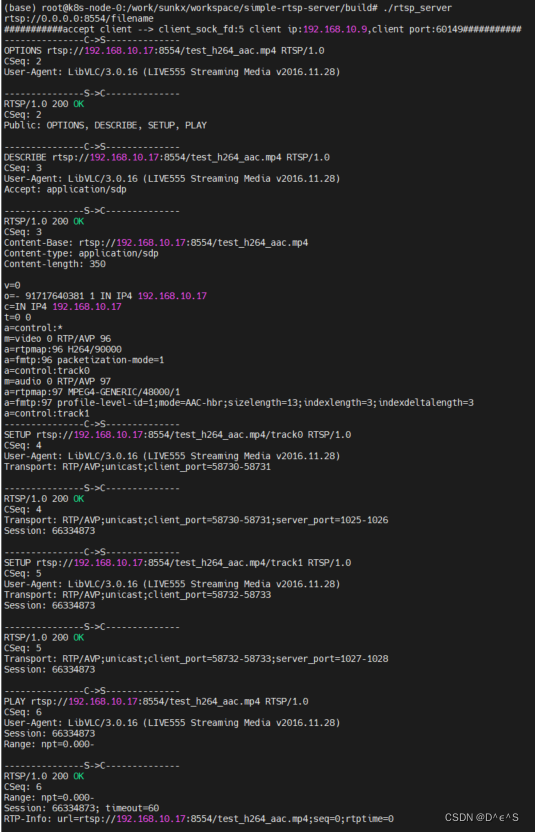
RTSP系列四:RTSP Server/Client实战项目
RTSP系列: RTSP系列一:RTSP协议介绍-CSDN博客 RTSP系列二:RTSP协议鉴权-CSDN博客 RTSP系列三:RTP协议介绍-CSDN博客 RTSP系列四:RTSP Server/Client实战项目-CSDN博客 目录 一、RTSP Server实战项目 1、准备 2、…...

sqli-labs-php7-master第11-16关
猜注入点 先来猜数字型 单引号字符型: 发现注入点找到了 猜测数据库有多少个字段: 1’ order by 4 # 密码随便输的。 这里没有使用--注释,因为没作用,可能是过滤掉了 继续猜。刚才没猜对 1 order by 2 # 没报错,猜…...

c++初阶 string的底层实现
string 基础函数成员成员变量构造函数析构函数:拷贝构造赋值构造 遍历下标访问迭代器 增删插开辟空间push_backappendinserterase 功能函数swapfindc_strsubstrclear 其他函数比较函数流提取<<流插入>>getline 完整版 声明:非纯手搓…...

微信小程序实现上传照片功能
案例: html: <view class"zhengjianCont fontSize30" style"margin-bottom: 40rpx;"><view class"kuai"><image binderror"imageOnloadError" bind:tap"upladPhoto" data-params"business…...

lombok安装成功但是找不到方法
2024.1.1版本的IDE的插件安装了默认的lombok(如图1),pom文件中也引入了lombok的依赖,在实体类写了Data的注解,当调用实体类的get和set方法运行时,报错找不到相应的方法,但是在调用get、set方法的…...

单细胞Seurat的umi矩阵-与feature、counts(用于质控)
目录 关于umi矩阵学习 用umi计算feature、counts值 ①meta数据查看 ②Count和Feature计算(生成Seurat时自动计算) 1)提取UMI矩阵 2)计算 其他指标 评估质量指标(重点) 1)UMI计数 2)基因计数 3)UMIs vs. genes detected 4)线粒体计数比率 5)综合过滤 过…...
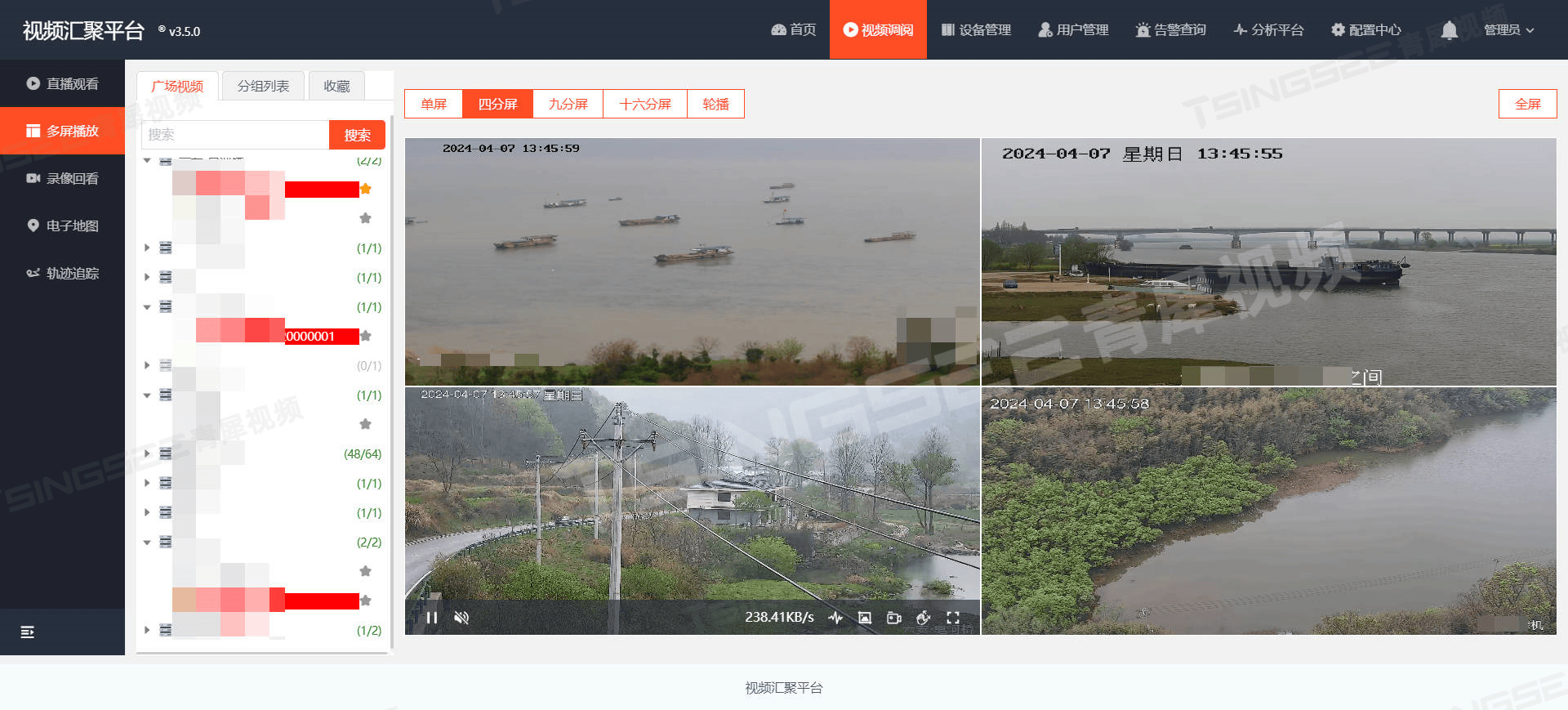
安防视频监控EasyCVR视频汇聚平台设备发送了GPS位置,但是订阅轨迹为空是什么原因?
安防视频监控EasyCVR视频汇聚平台兼容性强、支持灵活拓展,平台可提供视频远程监控、录像、存储与回放、视频转码、视频快照、告警、云台控制、语音对讲、GIS地图、轨迹跟踪、平台级联等视频能力。 用户描述,设备在电子地图中可以查看到定位信息ÿ…...

在 VueJS 中使用事件委托处理点击事件(事件委托,vue事件委托,什么是事件委托,什么是vue的事件委托)
前言 在开发 Vue 项目时,我们经常需要处理大量的点击事件。为每个可点击的元素单独添加事件监听器不仅会增加代码的复杂度,还会降低性能。事件委托是一种有效的优化方式,它可以显著减少事件监听器的数量,提高代码的可维护性和执行…...

密码学简史:时间密语
注:机翻,未校。 A brief history of cryptography: Sending secret messages throughout time Stemming from the Greek words for “hidden writing,” cryptography is the practice of encrypting transmitted information so that it can only b…...

【Java数据结构】---初始数据结构
乐观学习,乐观生活,才能不断前进啊!!! 我的主页:optimistic_chen 我的专栏:c语言 ,Java 欢迎大家访问~ 创作不易,大佬们点赞鼓励下吧~ 前言 从今天开始我们就要学习Java…...

MySQL--主从复制
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 一、什么是主从复制 1、定义 主从复制,是用来建立一个和主数据库完全一样的数据库环境,称为从数据库;主数据库一…...

Linux RT调度器之负载均衡
RT调度类的调度策略是:保证TopN(N为系统cpu个数)优先级的任务可以优先获得cpu资源。除了在任务选核时通过基于cpu优先级的选核策略保证这一点外,还有其它流程,我们姑且将这部分流程称作RT调度器的负载均衡(…...
--初识Pwn沙箱)
pwn学习笔记(8)--初识Pwn沙箱
初识Pwn沙箱 沙箱机制,英文sandbox,是计算机领域的虚拟技术,常见于安全方向。一般说来,我们会将不受信任的软件放在沙箱中运行,一旦该软件有恶意行为,则禁止该程序的进一步运行,不会对真实系…...
基础入门学习)
Day18_2--Vue.js Ajax(使用 Axios)基础入门学习
Vue.js 中的 Ajax 请求(使用 Axios) 什么是 Axios? Axios 是一个基于 Promise 的 HTTP 客户端,可以用于浏览器和 Node.js 环境中。它是现代化的 Ajax 库,用来替代传统的 XMLHttpRequest。 为什么选择 Axios…...

windows11远程桌面如何打开
随着远程办公的普及,选择合适的远程桌面工具变得尤为重要。在Windows 11上,用户可以利用系统自带的远程桌面功能,或选择更专业的第三方解决方案,如Splashtop。本文将详细介绍如何在Windows 11上启用远程桌面,并对比Win…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
