经典七大比较排序算法 · 下 + 附计数和基数排序
经典七大比较排序算法 · 下 + 附计数和基数排序
- 1 插入排序
- 1.1 算法思想
- 1.2 代码实现
- 1.3 插入排序特性
- 2 希尔排序
- 2.1 算法思想
- 2.2 代码实现
- 2.3 希尔排序特性
- 3 七大比较排序特性总结
- 4 计数排序
- 4.1 算法思想
- 4.2 代码实现
- 4.3 计数排序特性
- 5 基数排序
- 5.1 算法思想
- 5.2 代码实现
1 插入排序
1.1 算法思想
直接插入排序的基本思想就是,把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录都插入完为止,就得到一个新的有序序列。
只是看这种文字说明当然是有一点难以理解。其实在实际生活中,我们玩扑克牌时,就会不自觉地用到插入排序的思想。

我们可以从一端起,将新牌不断和手中的旧牌进行比较,来寻找合适的位置进行插入。插入之后保证手中的牌仍是有序的。
像扑克牌插入一样,这里给出直接插入排序的操作:
当插入第i(i≥1)i(i\ge 1)i(i≥1)个元素时,前面的array[0],array[1],…,array[i−1]array[0],array[1],…,array[i-1]array[0],array[1],…,array[i−1]已经排好序。此时用array[i]array[i]array[i]的排序码和array[i−1],array[i−2],...array[i-1],array[i-2],...array[i−1],array[i−2],...的排序码按顺序进行比较,找到待插入位置即可将array[i]array[i]array[i]插入,原来位置上的元素要按顺序依次后移。
插入排序视频演示
1.2 代码实现
在了解了插入排序的大致思想之后,可以来尝试将其实现。
插入排序有一个前提是在有序序列中进行插入。
那如何一开始就整一个有序序列呢?嘿嘿,一开始让其只有一个元素,一个元素不就可以看做有序序列了吗。
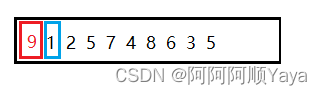
如图所示,要将上图数据进行排序。可以先将第一个数据9看做有序序列,让数据9后面的数据1对其进行插入排序。
这一次插入排序完成后,就得到如下图所示结果。
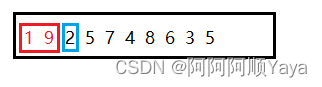
然后就是用数据2对前面的有序序列进行插入排序了。以此类推,如此反复。
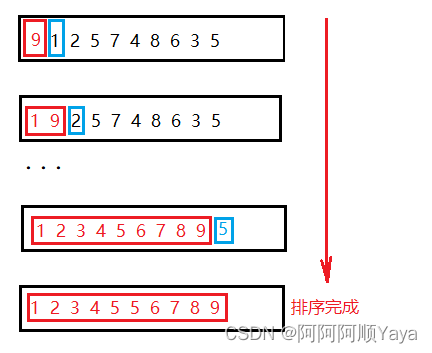
最终就可以将数据排好序了。
所以这里我们就可以假设一开始[0,end][0,end][0,end]是排好序的(end从0开始),将end+1end+1end+1位置的数据对其前面的有序序列进行插入排序,直到最后一个数据插入排序完成,整个序列也就有序了。
但还有一个点需要注意。
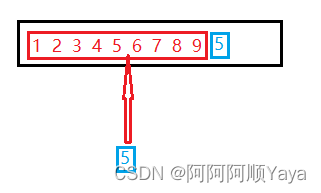
当插入数据时,可能是在序列之中进行插入。
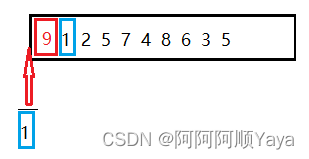
也可能是在序列最前面进行插入。
这两个地方的插入是略有不同的。因为这意味着插入排序两种不同的结束情况。需要有相应的判断条件来对插入排序进行终止。
鉴于以上的分析,这里给出如下参考实现代码:
//a - 待排序数组首地址
//n - 待排序数据个数
void InsertSort(int* a, int n)
{int i = 0;for (i = 0; i < n-1; ++i){//[0,end]有序,把end+1位置的值插入,保持有序//end区间为[0,n-2]int end = i;int tmp = a[end + 1];//当end<0,代表在序列最前面进行插入的情况(如数据1的插入)while (end >= 0){if (tmp < a[end]){//依次向后挪动覆盖a[end + 1] = a[end];--end;}else{//tmp>=a[end],代表在序列中间进行插入的情况(如数据5的插入)break;}}//插入数据a[end + 1] = tmp;}
}
1.3 插入排序特性
直接插入排序的特性是,待排序的序列越接近有序的情况下,直接插入排序的时间效率会越高。
因为序列越接近有序的情况下,待排序的数据比较的次数会越少,数据挪动的次数回越少。此时的时间复杂度是接近O(n)O(n)O(n)量级的。
但是,序列在无序情况下,或者最坏的逆序情况下,插入排序的时间复杂度是O(n2)O(n^2)O(n2)量级的。

比如像上图这样,数据8插入排序挪动 1 下,数据7插入排序挪动 2 下,数据6插入排序挪动 3 下,. . . 。
最终操作步骤累加起来会是一个等差数列,也就是O(n2)O(n^2)O(n2)量级的。
所以只能说,插入排序的适应性是很强的,在特定(接近有序)场景下的排序效果会非常出色。
2 希尔排序
希尔排序也称缩小增量排序,该方法因希尔(Donald Shell)于1959年提出而得名。

2.1 算法思想
希尔排序是对直接插入排序的优化改进,主要是基于插入排序的以下两点性质提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率是很高的,可以达到线性O(n)排序的效率。
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动1位。
针对以上两点,希尔大佬给出如下办法:
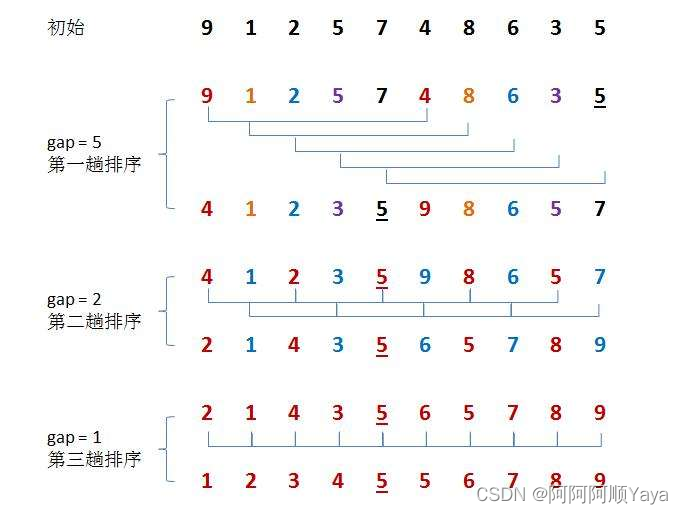
先选定一个整数gap,然后把待排序文件中的所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行直接插入排序。然后,不断缩小gap值,重复上述分组和排序的工作。当gap缩小到1时,所有记录在同一组内,进行直接插入排序,排完后记录就有序了。
总的来说,希尔排序分为两步:
- 第一步:
gap>1,分gap组,进行预排序 - 第二步:
gap=1,进行的是直接插入排序
这里第一步是针对插入排序第2点的劣势进行的改进。分成gap组,间隔为gap的数据为一组,每一次数据移动都是移动gap位,大大提高了排序的效率。
这里第二步是针对插入排序第1点的优势进行的利用。因为预排序的作用,使得记录已经处于接近有序的状态,这时利用插入排序很好的适应性,就可以实现非常高效的排序了。
但是,要说明的是,这个gap该如何选取呢?
1961年,IBM公司的女程序员 Marlene Metzner Norton(玛琳·梅茨纳·诺顿)首次使用 FORTRAN 语言编程实现了希尔排序算法。在其程序中使用了一种简易有效的方法设置希尔排序所需的增量序列(gap):第一个增量取待排序记录个数的一半,然后逐次减半,最后一个增量为1。该算法后来被称为 Shell-Metzner 算法,Metzner 本人在2003年的一封电子邮件中说道:“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”
现在希尔排序的实现中对于gap的选取主要用的有两种,都是和记录个数n(gap=n)相关:
gap=gap/3+1gap=gap/3+1gap=gap/3+1
gap=gap/2gap=gap/2gap=gap/2
两种方法都能保证最后一次排序中,gap等于1。
2.2 代码实现
因为希尔排序的起源还是插入排序,只是分成了gap组的插入排序。所以在代码实现上是有部分相似性的,如下图所示。
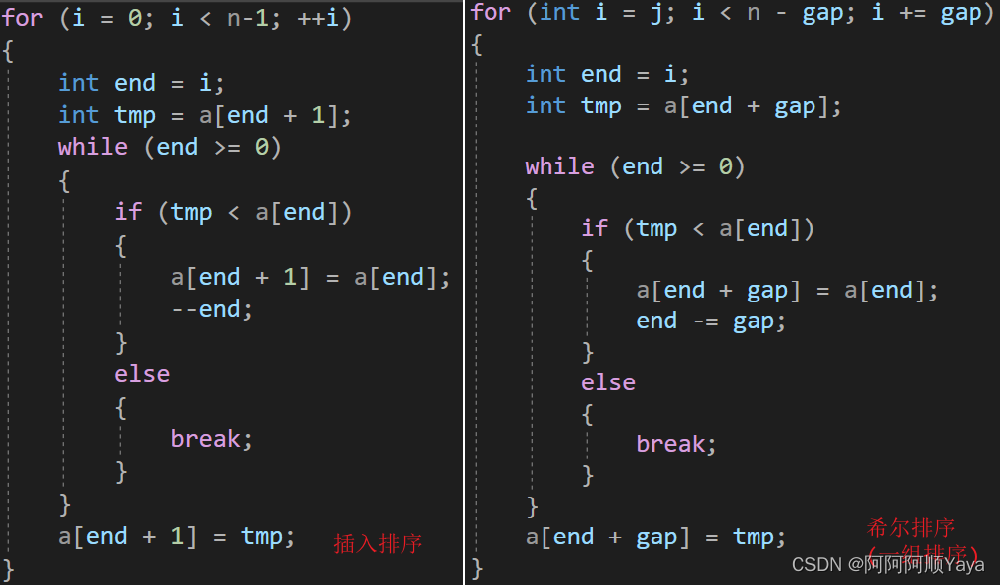
因为是分成gap组,所以一趟插入排序在希尔排序中只能排一组。所以执行gap次也就可以实现gap个组的插入排序了。
for (int j = 0; j < gap; ++j)
{for (int i = j; i < n - gap; i += gap){......}
}
此时这样的一趟执行完之后,只是完成了一趟预排序。gap>1,仍需继续循环执行该操作。所以,
while (gap > 1)
{gap = gap / 3 + 1;for (int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){......}}
}
通过上面的铺垫,下面就可以给出完整的希尔排序过程了。
//n - 数据个数
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
但是,上面的代码还可以进行一下优化。
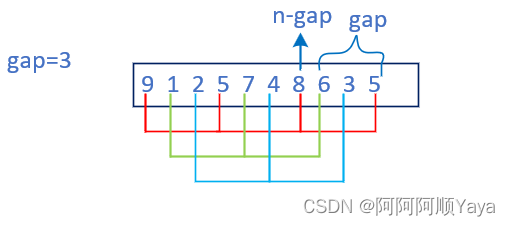
for (int j = 0; j < gap; ++j)
{for (int i = j; i < n - gap; i += gap){......}
}//将两个循环合并成一个循环
for (int i = 0; i < n - gap; ++i)
{......
}
这样就将原本是一组插入排序完之后再执行另一组的过程,转变成gap组交替执行的过程。
只是代码上的简化,大思想还是不变的。
2.3 希尔排序特性
希尔算法的性能与所选取的分组长度序列有很大关系。只对特定的待排序记录序列,可以准确地估算关键词的比较次数和对象移动次数。但想要弄清关键词比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,迄今仍然是数学上难题。
所以,希尔排序确切的时间复杂度是很难计算的,很多书上给出的希尔排序的时间复杂度也都不尽相同。
《数据结构(C语言版) – 严蔚敏》
希尔排序的分析是一个复杂度问题,因为它的时间是所取“增量”序列的函数,这涉及一些数学上尚未解决的难题。因此,到目前为止,尚未有人求得一种最好的增量序列,但大量的研究已得出一些局部的结论。如有人指出,当增量序列为dlta[k]=2t−k+1−1dlta[k]=2^{t-k+1}-1dlta[k]=2t−k+1−1时,希尔排序的时间复杂度为O(n3/2)O(n^{3/2})O(n3/2),其中ttt为待排序趟数,1≤k≤t≤log2(n+1)1\leq k\leq t\leq log_2(n+1)1≤k≤t≤log2(n+1)。还有人在大量的实验基础上推出:当nnn在某个特定范围内,希尔排序所需的比较和移动次数约为n1.3n^{1.3}n1.3,当n→∞n\rightarrow\infinn→∞时,可减少到n(log2n)2n(log_2n)^2n(log2n)2。增量序列可以有各种取法,但需注意:应使增量序列中的值没有除 1 之外的公因子,并且最后一个增量值必须等于1。
《数据结构-用面向对象方法与C++描述》-- 殷人昆
gap的取法有多种。最初Shell提出取gap=[n/2]gap=[n/2]gap=[n/2],gap=[gap/2]gap=[gap/2]gap=[gap/2],直到gap=1gap=1gap=1,后来Knuth提出取gap=[gap/3]+1gap=[gap/3]+1gap=[gap/3]+1。还有人提出取奇数为好,也有人提出各gapgapgap互质为好。无论哪一种主张都没有得到证明。
对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算关键码的比较次数和对象移动次数,但想要弄清关键码比较次数和对象移动次数与增量选择之间的依赖关系,并给出完整的数学分析,还没有人能够做到。在Knuth所著的《计算机程序设计技巧》第3卷中,利用大量的实验统计资料得出,当nnn很大时,关键码平均比较次数和对象移动次数大约在n1.25n^{1.25}n1.25到1.6n1.251.6n^{1.25}1.6n1.25范围内,这是利用直接插入排序作为子序列排序方法的情况下得到的。
上面代码中的gap是按照Knuth提出的方式取值的。而Kunth进行了大量的试验统计,所以上面代码实现的希尔排序时间复杂度可以用O(n1.25)O(n^{1.25})O(n1.25)到O(1.6∗n1.25)O(1.6*n^{1.25})O(1.6∗n1.25)这个范围作参考。
3 七大比较排序特性总结
稳定性介绍:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次
序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则这种排序算法是稳定的;否则是不稳定的。
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 直接插入排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 希尔排序 | 取平均时间复杂度:O(n1.3)O(n^{1.3})O(n1.3) | \ | O(1)O(1)O(1) | 不稳定 |
| 选择排序 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 不稳定 |
| 堆排序 | O(n∗log2n)O(n*log_2n)O(n∗log2n) | O(n∗log2n)O(n*log_2n)O(n∗log2n) | O(1)O(1)O(1) | 不稳定 |
| 冒泡排序 | O(n)O(n)O(n) | O(n2)O(n^2)O(n2) | O(1)O(1)O(1) | 稳定 |
| 快速排序 | O(n∗log2n)O(n*log_2n)O(n∗log2n) | O(n2)O(n^2)O(n2) | O(log2n)O(log_2n)O(log2n) | 不稳定 |
| 归并排序 | o(n∗log2n)o(n*log_2n)o(n∗log2n) | o(n∗log2n)o(n*log_2n)o(n∗log2n) | O(n)O(n)O(n) | 稳定 |
4 计数排序
4.1 算法思想
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中,是对哈希直接定址法的变形应用。
操作步骤:
- 找出待排序的数组中最大和最小的元素
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
计数排序视频演示
4.2 代码实现
void CountSort(int* a, int n)
{//找出待排序的数组中最大和最小的元素 int min = a[0];int max = a[0];for (int i = 1; i < n; ++i){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}//统计次数的数组int range = max - min + 1;int* countArray = (int*)calloc(range, sizeof(int));assert(countArray);//统计次数for (int i = 0; i < n; ++i){++countArray[a[i] - min];}//回写-排序int j = 0;for (int i = 0; i < range; ++i){//出现几次就回写几个min+iwhile (countArray[i]--){a[j++] = min + i;}}
}
上面代码采用了相对映射而非绝对映射,如果使用绝对映射,空间可能浪费太严重。
4.3 计数排序特性
计数排序以及桶排序,计数排序作为非比较排序,一般都只能用于对整数的排序,可用范围比较窄。
计数排序的局限性:
- 如果是浮点数,字符串等就不能用了
- 如果数据范围很大,空间复杂度会很高,相对不适合。(适合范围集中,重复数据多)
但在适用的场景下,时间复杂的是很好的,一般都是线性时间复杂度。
5 基数排序
5.1 算法思想
基数排序是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。
其核心思想是对数据的分发和回收。
基数排序视频演示
5.2 代码实现
计数排序的实现需要借助队列来完成,因为是使用C语言实现,如果需要可以参考阿顺的这篇博文链式队列(C语言实现)。
这里按照LSD法,即最低为优先来进行计数排序。
//首先建立RADIX(基数)个队列
Queue queue[RADIX];
for (int i = 0; i < RADIX; ++i)
{QueueInit(&queue[i]);
}
//[left, right)
void RadixSort(int* a, int left, int right)
{//K - 数据最高的位数for (int i = 0; i < K; ++i){//分发数据Distribute(a, left, right, i);//回收数据Collect(a);}
}int getKey(int value, int k)
{int key = 0;while (k >= 0){key = value % 10;value /= 10;--k;}return key;
}
void Distribute(int* a, int left, int right, int k)
{for (int i = left; i < right; ++i){//获取这一趟分发,a[i]数据的基数值int key = getKey(a[i], k);QueuePush(&queue[key], a[i]);}
}
void Collect(int* a)
{int j = 0;for (int i = 0; i < RADIX; ++i){while (!QueueEmpty(&queue[i])){a[j++] = QueueFront(&queue[i]);QueuePop(&queue[i]);}}
}
最后不要忘了销毁队列。
相关文章:

经典七大比较排序算法 · 下 + 附计数和基数排序
经典七大比较排序算法 下 附计数和基数排序1 插入排序1.1 算法思想1.2 代码实现1.3 插入排序特性2 希尔排序2.1 算法思想2.2 代码实现2.3 希尔排序特性3 七大比较排序特性总结4 计数排序4.1 算法思想4.2 代码实现4.3 计数排序特性5 基数排序5.1 算法思想5.2 代码实现1 插入排…...
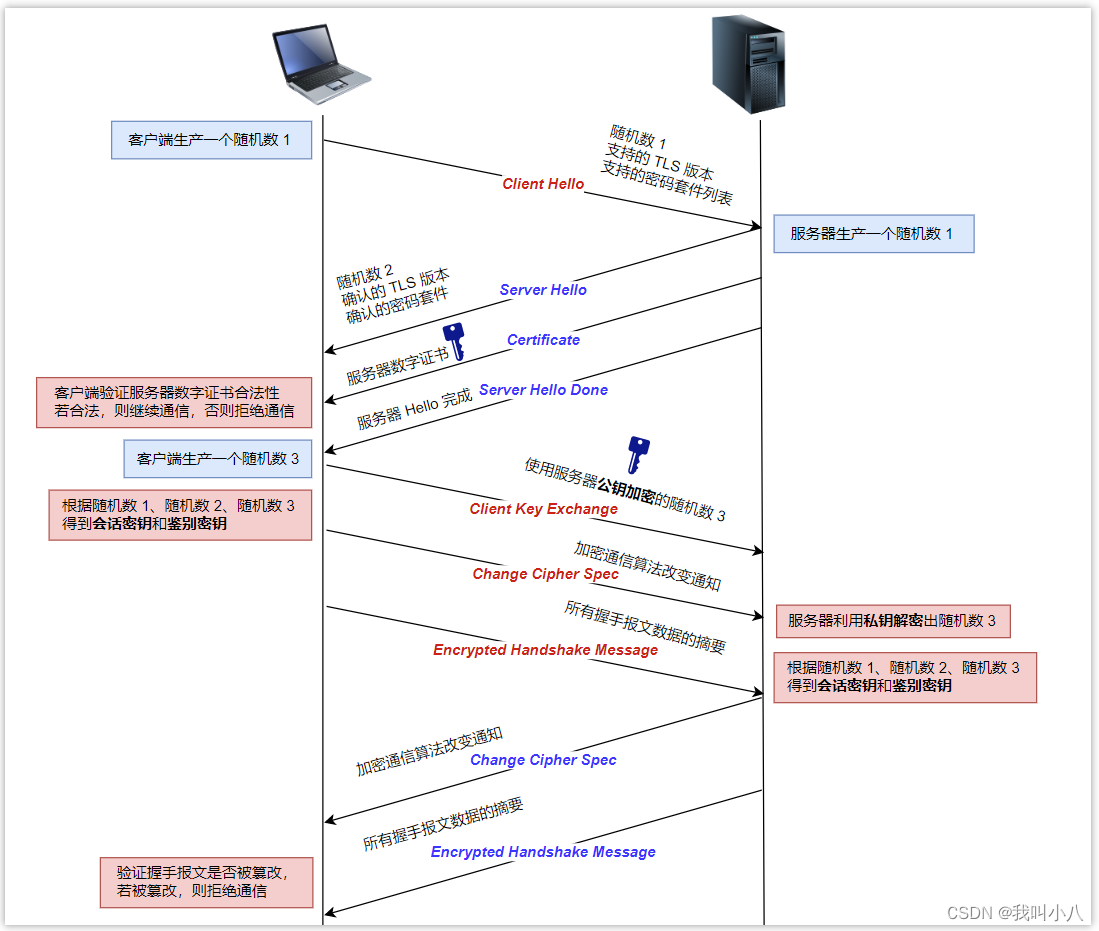
HTTPS协议,看这篇就够了
不安全的HTTP 近些年来,越来越多的网站使用 HTTPS 协议进行数据传输,原因在于 HTTPS 相较于 HTTP 能够提供更加安全的服务。 很多浏览器对于使用 HTTP 协议的网站会加上『警告』的标志表示数据传输不安全,而对于使用 HTTPS 协议的网站会加上…...

C语言学习之路--结构体篇
目录一、前言二、结构体的声明1、结构的基础知识2、结构的声明3、结构体成员的类型4、结构体变量的定义和初始化三、结构体成员的访问四、结构体传参一、前言 本人是一名小白,这一篇是记录我C语言学习中的结构体的所学所得,仅为简单的认识下C语言中的各…...
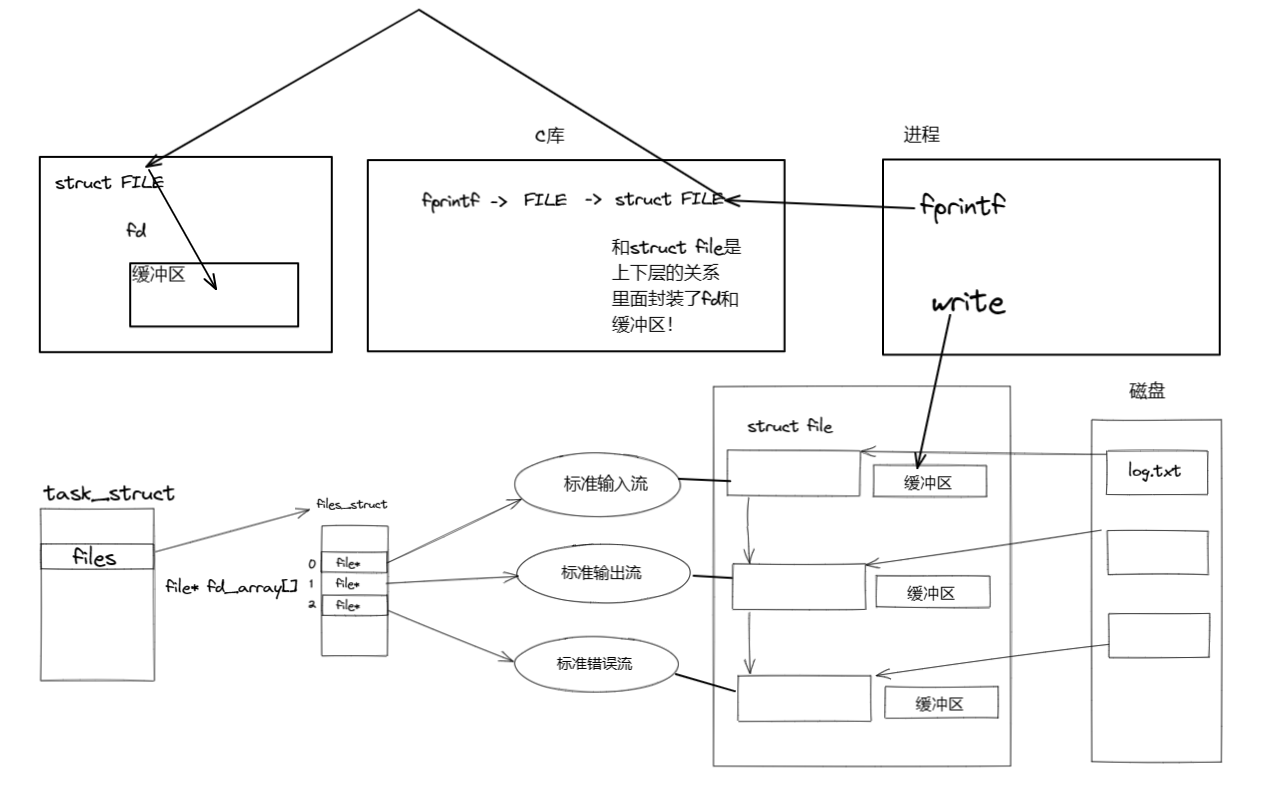
【LINUX】初识文件系统
文章目录一、前言二、回顾C语言文件操作三、初识系统调用openreadwriteclose四、文件系统初识五、结语一、前言 二、回顾C语言文件操作 int main() {FILE* fp fopen("log.txt", "w");if (fp NULL){perror("fopen");}int cnt 0;fputs("…...

金三银四Java面试题及答案整理(2023最新版) 持续更新
作为一名优秀的程序员,技术面试是不可避免的一个环节,一般技术面试官都会通过自己的方式去考察程序员的技术功底与基础理论知识。 如果你参加过一些大厂面试,肯定会遇到一些这样的问题: 1、看你项目都用的框架,熟悉 …...

7个角度,用 ChatGPT 玩转机器学习
大家好,我是机器学习科普创作者章北海mlpy,探索更高效的学习方法是我一直等追求。现在的初学者太幸福了,可以利用ChatGPT来帮助你学习机器学习的各个方面。 比如【个人首测】百度文心一言 VS GPT-4这篇文章中,我就用文心一言、GP…...
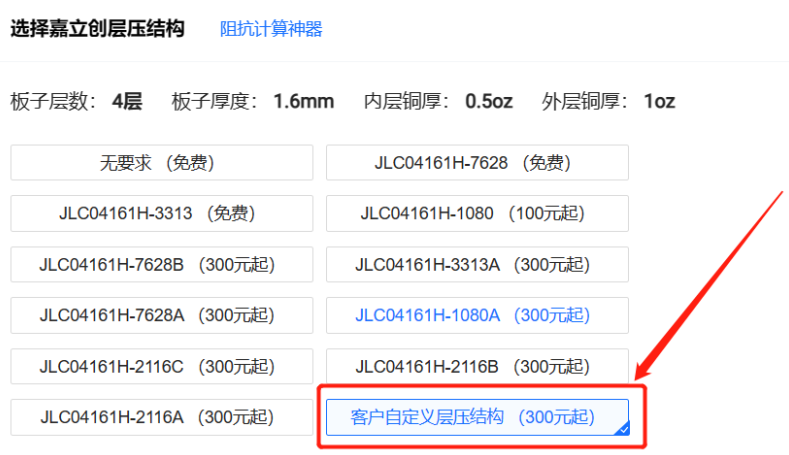
关于多层板,你了解多少?
01 前言 大家好,我是张巧龙。好久没写原创了,记得之前刚接触PCB时,还在用腐蚀单层板,类似这种。 慢慢随着电子产品功能越来越多,产品越来越薄,对PCB设计要求越来越高了,复杂程度也随之增加。因此…...

使用sqlalchemy-gbasedbt连接GBase 8s数据库
测试环境: 操作系统:CentOS 7.9 64-bit数据库版本:GBase8sV8.8_AEE_3.0.0_1,对应的CSDK版本为3.0.0_1 1,确认安装python3 确认已经安装python3和python3-devel [rootlocalhost test]# python3 -V Python 3.6.8如果…...

前端如何丢掉你的饭碗?
对于后端而言,我们常有“删库跑路”的说法,这说明后端的操作对于信息系统而言通常影响很大,可以轻易使信息系统宕机、崩溃,直接导致项目失败。所以,不要去逼后端程序员! 作为前端程序员,我们似…...
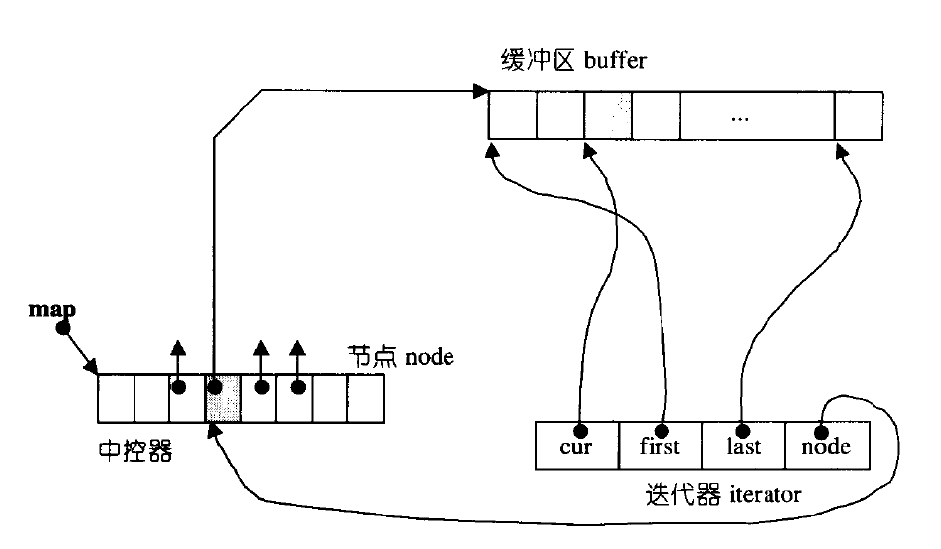
栈、队列、优先级队列的模拟实现
优先级队列的模拟实现栈stack的模拟实现push()pop()top()size()empty()swap()stack总代码队列queue的模拟实现push()pop()front()back()empty()size()swap()queue总代码优先级队列(堆)push()pop()top()empty()size()swap()priority_queue总代码deque的了解栈 在CSTL中栈并不属…...
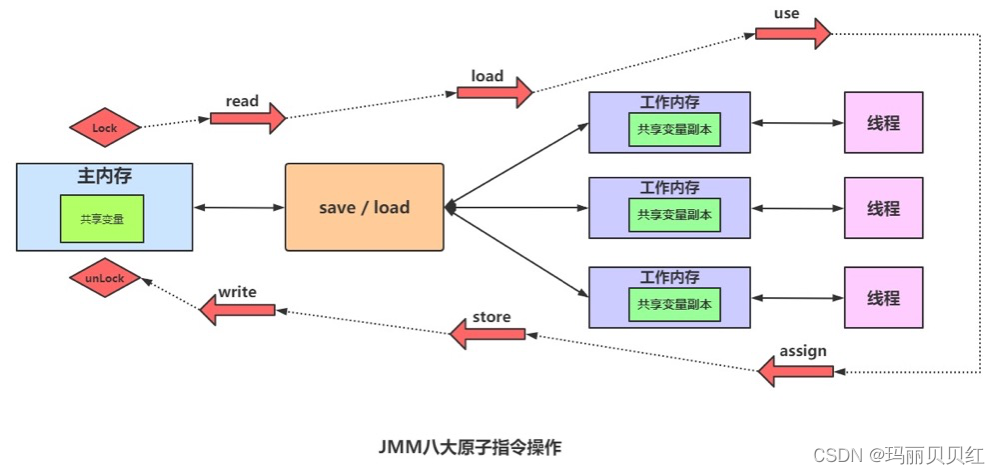
JMM内存模型
JMM内存模型JMM内存模型定义三大特性原子性可见性有序性volatile语义JMM规则操作系统实现术语缓存一致性要求缓存一致性机制写传播事务串行化重排序as-if-serial 语义(像是有序的)happens-before 原则happens-before 原则的八大子原则内存屏障总结finalf…...

Linux- 系统随你玩之--玩出花活的命令浏览器-双生姐妹花
文章目录1、背景2、命令浏览器-双生姐妹花2.1、姐妹花简介2.2 、验名正身2.3、常用功能选项3、常用实操3.1、发送请求获取文件3.1.1、抓取页面内容到一个文件中3.1.2、多个文件下载3.1.3、下载ftp文件3.1.4、断点续传3.1.5、上传文件3.1.6、内容输出3.2 、利用curl测试接口3.3 …...

【深度学习】基于Hough变化的答题卡识别(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。⛳座右铭&#…...

Linux - 进程控制(创建和终止)
1.进程创建fork函数初识 在linux中fork函数时非常重要的函数,它从已存在进程中创建一个新进程。新进程为子进程,而原进程为父进程。返回值:子进程返回0,父进程返回子进程id,出错返回-1getpid()获取子进程id,…...
依赖注入~
依赖注入之setter注入: 依赖注入是IOC具体的一种实现方式, 这是针对资源获取的方式角度来说的,之前我们是被动接受,现在IOC具体的实现叫做依赖注入,从代码的角度来说,原来创建对象的时候需要new࿰…...
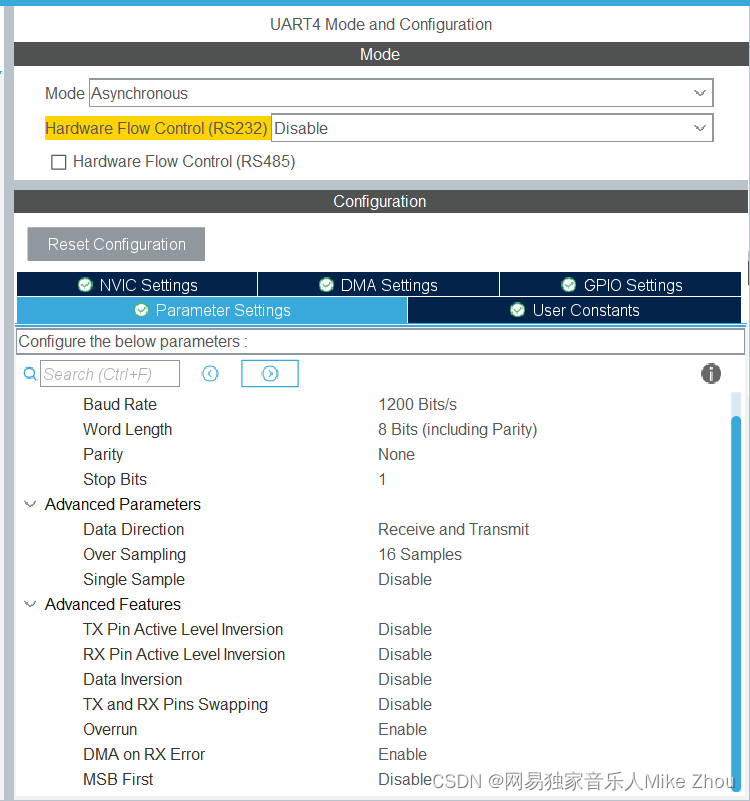
【嵌入式硬件芯片开发笔记】HART协议调制解调芯片AD5700配置流程
【嵌入式硬件芯片开发笔记】HART协议调制解调芯片AD5700配置流程 XTAL_EN接地,CLK_CFG的两个引脚由同一个GPIO控制 初始时HART_CLK_CFG输出低电平 由RTS引脚控制调制/解调。当RTS处于高电平时,为解调(输入);否则为调…...

Go语言异步下载视频
异步下载mp4视频列表 下面是一个简单的Go语言示例,用于异步下载视频。我们将使用goroutines来实现异步下载,并使用sync.WaitGroup来等待所有下载任务完成。此示例依赖于net/http包来执行HTTP请求。 package mainimport ("fmt""io"…...
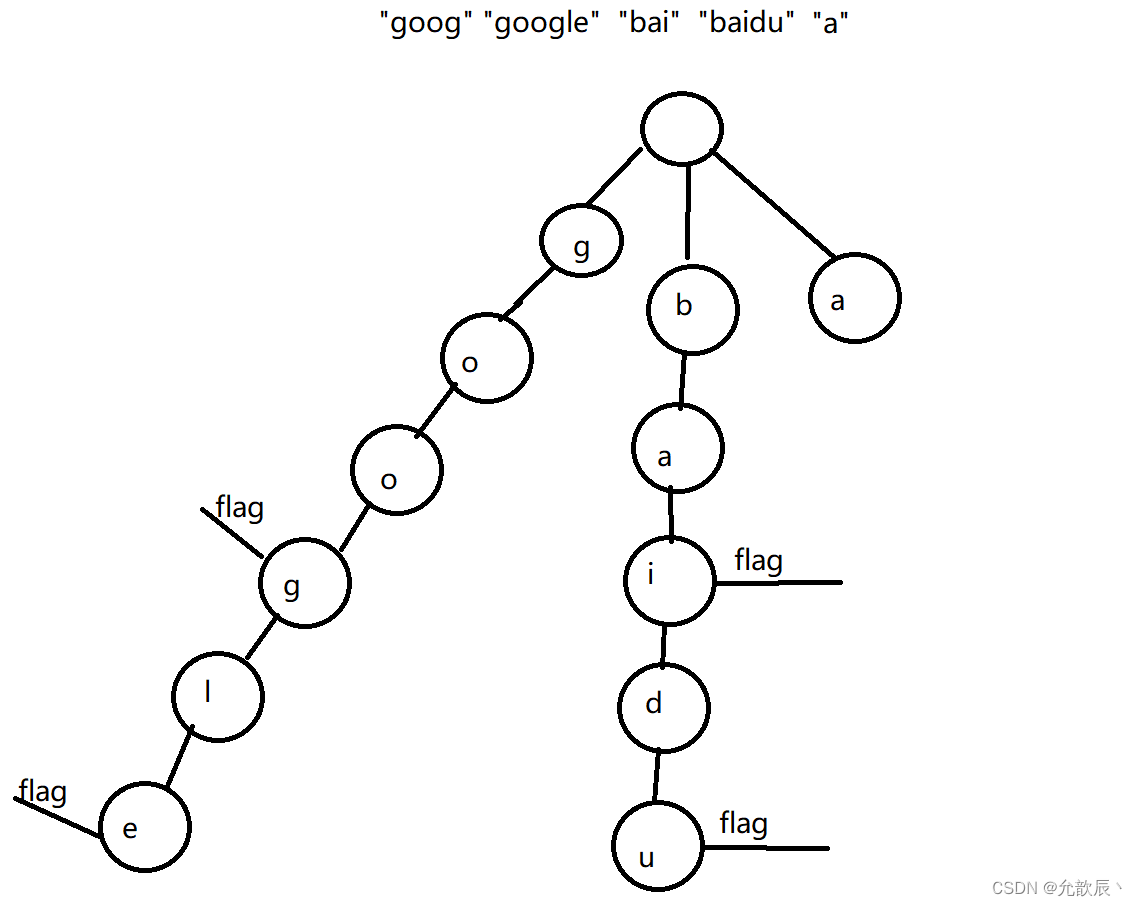
前缀树(字典树/Trie) -----Java实现
目录 一.前缀树 1.什么是前缀树 2.前缀树的举例 二.前缀树的实现 1.前缀树的数据结构 1.插入字符串 2.查找字符串 3.查找前缀 三.词典中最长的单词 1.题目描述 2.问题分析 3.代码实现 一.前缀树 1.什么是前缀树 字典树(Trie树)是一种树形…...

申请专利需要具备什么条件
申请专利需要具备什么条件 在我国,如果创造出来了新的发明都可以申请专利权,一旦申请成功之后,自己的发明就受到了法律的保护,任何人不得以违法的手段进行侵犯。那么申请专利需要具备什么条件?今天律赢时代网就为大家…...

【C++】一篇带你搞懂C++“引用”
前言在C语言的学习中,并没有引用这个概念,但是在C中,加入了引用这个概念,说明引用也是很重要的,但是我们怎么理解引用呢?我是这么理解的,例如在水浒传中,108个英雄好汉都是自己的外号…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
