acm省赛:高桥和低桥(三种做法:区间计数、树状数组、线段树)
题目描述
有个脑筋急转弯是这样的:有距离很近的一高一低两座桥,两次洪水之后高桥被淹了两次,低桥却只被淹了一次,为什么?答案是:因为低桥太低了,第一次洪水退去之后水位依然在低桥之上,所以不算“淹了两次”。举例说明:
假定高桥和低桥的高度分别是5和2,初始水位为1
第一次洪水:水位提高到6(两个桥都被淹),退到2(高桥不再被淹,但低桥仍然被淹)
第二次洪水:水位提高到8(高桥又被淹了),退到3。
没错,文字游戏。关键在于“又”的含义。如果某次洪水退去之后一座桥仍然被淹,那么下次洪水来临水位提高时不能算“又”淹一次。
输入n座桥的高度以及第i次洪水的涨水水位ai和退水水位bi,统计有多少座桥至少被淹了k次。初始水位为1,且每次洪水的涨水水位一定大于上次洪水的退水水位。
输入
输入文件最多包含25组测试数据。每组数据第一行为三个整数n, m, k(1<=n,m,k<=105)。第二行为n个整数hi(2<=hi<=108),即各个桥的高度。以下m行每行包含两个整数ai和bi(1<=bi<ai<=10^8, ai>bi-1)。输入文件不超过5MB。
输出
对于每组数据,输出至少被淹k次的桥的个数。
样例输入
2 2 2
2 5
6 2
8 3
5 3 2
2 3 4 5 6
5 3
4 2
5 2
样例输出
Case 1: 1
Case 2: 3
分析
这道题的n是1e5,暴力是没办法解开的。容易把所有的桥按照高度从小到大进行排序,然后定义一个数组记录每个高桥被淹的次数,根据输入的数据中的高水位和上一次水位得到会被淹的桥的区间,这里的复杂度是O(mlogn),接下来就是对这个区间所有数进行++操作,然而最坏的情况是得到的区间有n那么大,直接在m的循环体内再循环进行区间++操作的复杂度会达到O(mn),将会超时。
看到区间的操作就要想到线段树或者树状数组,当然这道题利用区间计数的思想是最快的。
方法一:区间计数
定义一个数组cnt初始化为0,对于每次操作,得到区间[l,r]以后,实际上我们每次只需要将cnt[l]++,将cnt[r+1]–。等到操作全部完成后遍历cnt[1~n],对于每个cnt[i],都加上之前的cnt[i-1],即可得到i桥被淹没的次数
具体原理也不难理解,可以用一种离散数学的思维来证明,但是我发现我打不清楚里面的话,要是证明不了就自己多写几个例子很容易就能体会到。
代码如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+5;
int n,m,k,h[maxn],cnt[maxn],t=1;
int main(){while(~scanf("%d%d%d",&n,&m,&k)){memset(cnt,0,sizeof(cnt));for(int i=0;i<n;++i)scanf("%d",&h[i]);sort(h,h+n);int last=1;for(int i=0;i<m;++i){int a,b;scanf("%d%d",&a,&b);int id1=lower_bound(h,h+n,a)-h;if(h[id1]>a)id1--;int id2=upper_bound(h,h+n,last)-h;cnt[id2]++,cnt[id1+1]--;last=b;}for(int i=1;i<n;++i)cnt[i]+=cnt[i-1];int ans=0;for(int i=0;i<n;++i)if(cnt[i]>=k)ans++;printf("Case %d: %d\n",t++,ans);}
}
方法二:树状数组
既然涉及到了区间+的操作,树状数组肯定也可以考虑在内,思维上差不多。
代码如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+5;
int n,m,k,h[maxn],t=1;
int f[maxn];
inline int lowbit(int x){return x&-x;}
inline void add(int x,int num){for(;x<=n;x+=lowbit(x))f[x]+=num;
}
inline int query(int x){int ans=0;for(;x>0;x-=lowbit(x))ans+=f[x];return ans;
}
int main(){while(~scanf("%d%d%d",&n,&m,&k)){memset(f,0,sizeof(f));int pre=0;for(int i=1;i<=n;++i)scanf("%d",&h[i]);sort(h+1,h+n+1);int last=1;while(m--){int a,b;scanf("%d%d",&a,&b);int id1=lower_bound(h+1,h+n+1,a)-h;if(h[id1]>a)id1--;int id2=upper_bound(h+1,h+n+1,last)-h;add(id2,1),add(id1+1,-1);last=b;}int ans=0;for(int i=1;i<=n;++i)if(query(i)>=k)ans++;printf("Case %d: %d\n",t++,ans);}
}
方法三:线段树
线段树,有坑的。。
对于一个线段树来说,每次加的大小只有1其实已经够舒服的了,但是这个x和y,真的得同时把控到位,而且要如果你不是我这样的方法找到这个区间的话,还得调一下的,直接给代码:
代码如下(线段树的建树+懒标记下放):
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int n,m,K,h[N],Case=1;
struct Tree{int val,add,len;
}t[4*N];
inline void buildtree(int k,int l,int r){t[k].add=0,t[k].len=(r-l+1);if(l==r){t[k].val=0;return;}int mid=(l+r)>>1;buildtree(k<<1,l,mid);buildtree(k<<1|1,mid+1,r);t[k].val=t[k<<1].val+t[k<<1|1].val;
}
inline void push_down(int k){t[k<<1].add+=t[k].add,t[k<<1|1].add+=t[k].add;t[k<<1].val+=t[k].add*t[k<<1].len;t[k<<1|1].val+=t[k].add*t[k<<1|1].len;t[k].add=0;
}
inline void push_up(int k){t[k].val=t[k<<1].val+t[k<<1|1].val;
}
inline void add(int k,int l,int r,int x,int y){if(l==x&&r==y){t[k].val+=t[k].len;t[k].add++;return;}push_down(k);int mid=(l+r)>>1;if(y<=mid)add(k<<1,l,mid,x,y);elseif(x>mid)add(k<<1|1,mid+1,r,x,y);else add(k<<1,l,mid,x,mid),add(k<<1|1,mid+1,r,mid+1,y);push_up(k);
}
inline int query(int k,int l,int r,int x,int y){if(l==x&&r==y)return t[k].val;push_down(k);int mid=(l+r)>>1;if(y<=mid)return query(k<<1,l,mid,x,y);elseif(x>mid)return query(k<<1|1,mid+1,r,x,y);else return query(k<<1,l,mid,x,mid)+query(k<<1|1,mid+1,r,mid+1,y);
}
int main(){while(~scanf("%d%d%d",&n,&m,&K)){for(int i=1;i<=n;++i)scanf("%d",&h[i]);sort(h+1,h+n+1);buildtree(1,1,n);int last=1;while(m--){int a,b;scanf("%d%d",&a,&b);int x=upper_bound(h+1,h+n+1,last)-h;int y=lower_bound(h+1,h+n+1,a)-h;if(y>n||h[y]>a)y--;last=b;if(x>n)continue;if(x<=y)add(1,1,n,x,y);}int ans=0;for(int i=1;i<=n;++i)if(query(1,1,n,i,i)>=K)ans++;printf("Case %d: %d\n",Case++,ans);}
}
总结
对于区间类型的题目,能构思出树状数组最好还是用树状数组来解决,有时候线段树不仅敲的很多,效率还是最低的。
相关文章:

acm省赛:高桥和低桥(三种做法:区间计数、树状数组、线段树)
题目描述 有个脑筋急转弯是这样的:有距离很近的一高一低两座桥,两次洪水之后高桥被淹了两次,低桥却只被淹了一次,为什么?答案是:因为低桥太低了,第一次洪水退去之后水位依然在低桥之上ÿ…...

stm32-定时器详解
0. 概述 本文针对STM32F1系列,主要讲解了其中的8个定时器的原理和功能 1. 定时器分类 STM32F1 系列中,除了互联型的产品,共有 8 个定时器,分为基本定时器,通用定时器和高级定时器基本定时器 TIM6 和 TIM7 是一个 16 位…...
《硬件架构的艺术》读书笔记:Chapter 1 亚稳态的世界
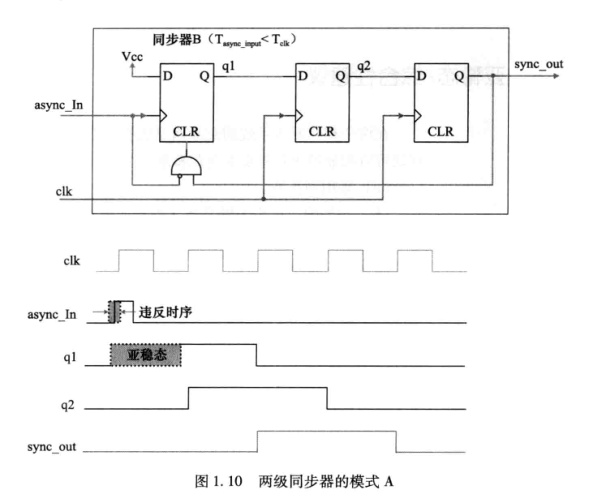
Chapter 1 亚稳态的世界 一、简介 同步系统中,数据和时钟有固定的因果关系(在同一时钟域(Clock Domains))中,只要数据和时钟满足建立时间和保持时间的要求,不会产生亚稳态(meastable) 静态时序分析(STA) 就是基于同步电路设计模型而出现的&am…...
开箱即用的密码框组件
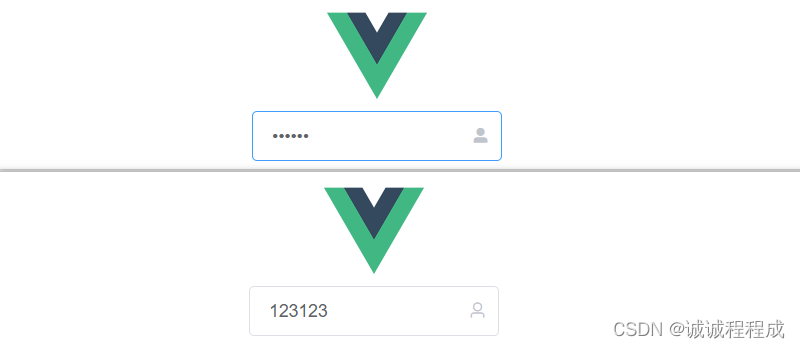
写了一个小玩具,分享一下 - 组件功能: 初次进入页面时,密码隐藏显示,且无法查看真实密码 当修改密码时,触发键盘,输入框则会直接清空 此时输入密码,可以设置密码的隐藏或显示: …...

ChatGPT能否取代程序员?
目录ChatGPT能否取代程序员?ChatGPT和程序员的工作内容和工作方式ChatGPT和程序员的共同点程序员的优势程序员的实力ChatGPT和程序员的关系结论惊喜ChatGPT能否取代程序员? ChatGPT是一种非常普遍的人工智能(AI)系统,…...

案例分享 | 金融微服务场景下如何提升运维可观测性
云原生环境下金融业务的微服务化改造以及分布式架构的部署,使得业务与开发部门的关联更为紧密,传统运维监控已满足不了业务运营需求,亟需建设具备可观测性的运维体系。所以这次我们以某金融客户的实践案例为例,跟大家说一说在金…...
)
CentOS8提高篇3:Centos8安装播放器(mplayer vlc)
1. 准备工作(需要配置epel, rpmfusion源); 配置epel源 下载epel dnf install epel-release 配置rpmfusion源 下载rpmforge dnf install rpmfusion-free-release-8.noarch.rpm 2. 安装mplayer和vlc 直接dnf安装 # dnf install mplayer # dnf install v…...

MySQL-存储过程
什么是存储过程我们前面所学习的MySQL语句都是针对一个表或几个表的单条 SQL 语句,但是在数据库的实际操作中,并非所有操作都那么简单,经常会有一个完整的操作需要多条SQL语句处理多个表才能完成。例如,为了确认学生能否毕业&…...
经典七大比较排序算法 · 下 + 附计数和基数排序
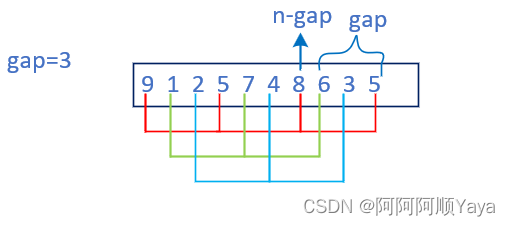
经典七大比较排序算法 下 附计数和基数排序1 插入排序1.1 算法思想1.2 代码实现1.3 插入排序特性2 希尔排序2.1 算法思想2.2 代码实现2.3 希尔排序特性3 七大比较排序特性总结4 计数排序4.1 算法思想4.2 代码实现4.3 计数排序特性5 基数排序5.1 算法思想5.2 代码实现1 插入排…...
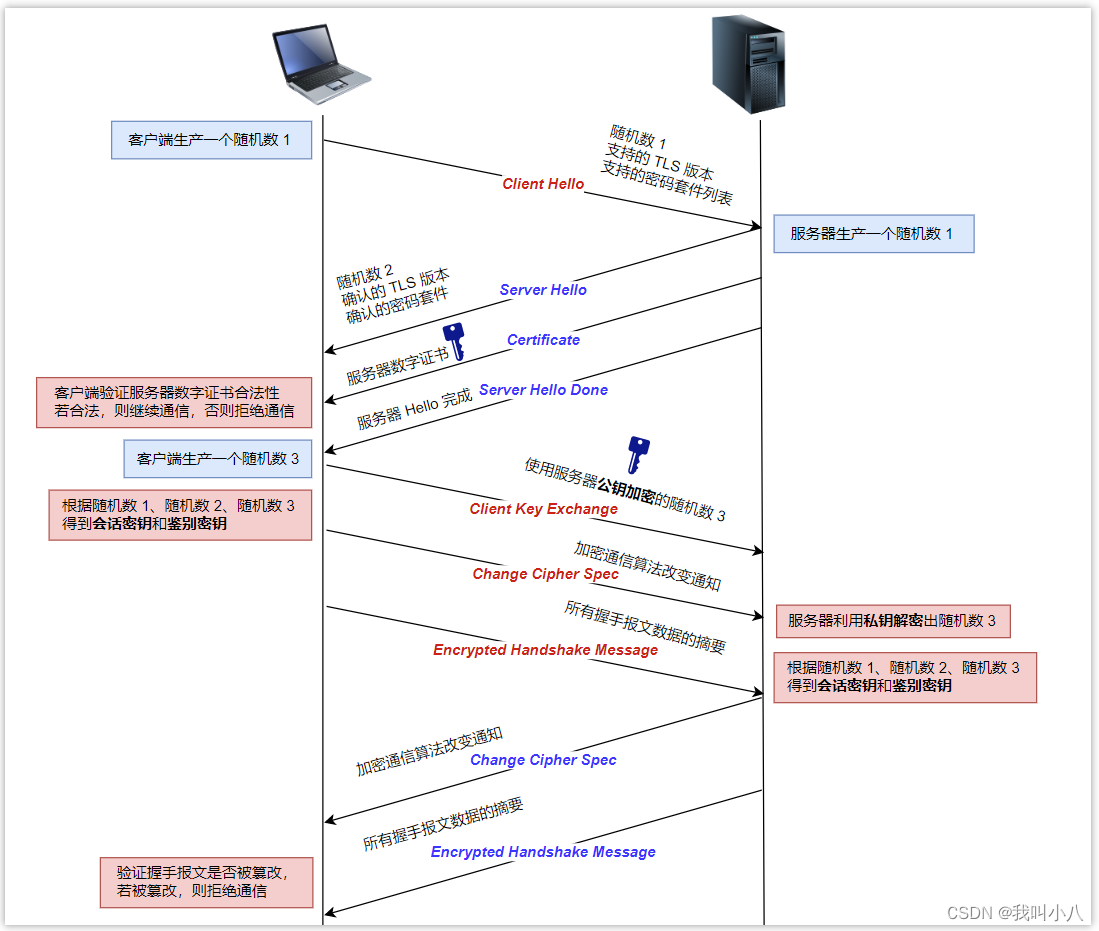
HTTPS协议,看这篇就够了
不安全的HTTP 近些年来,越来越多的网站使用 HTTPS 协议进行数据传输,原因在于 HTTPS 相较于 HTTP 能够提供更加安全的服务。 很多浏览器对于使用 HTTP 协议的网站会加上『警告』的标志表示数据传输不安全,而对于使用 HTTPS 协议的网站会加上…...

C语言学习之路--结构体篇
目录一、前言二、结构体的声明1、结构的基础知识2、结构的声明3、结构体成员的类型4、结构体变量的定义和初始化三、结构体成员的访问四、结构体传参一、前言 本人是一名小白,这一篇是记录我C语言学习中的结构体的所学所得,仅为简单的认识下C语言中的各…...
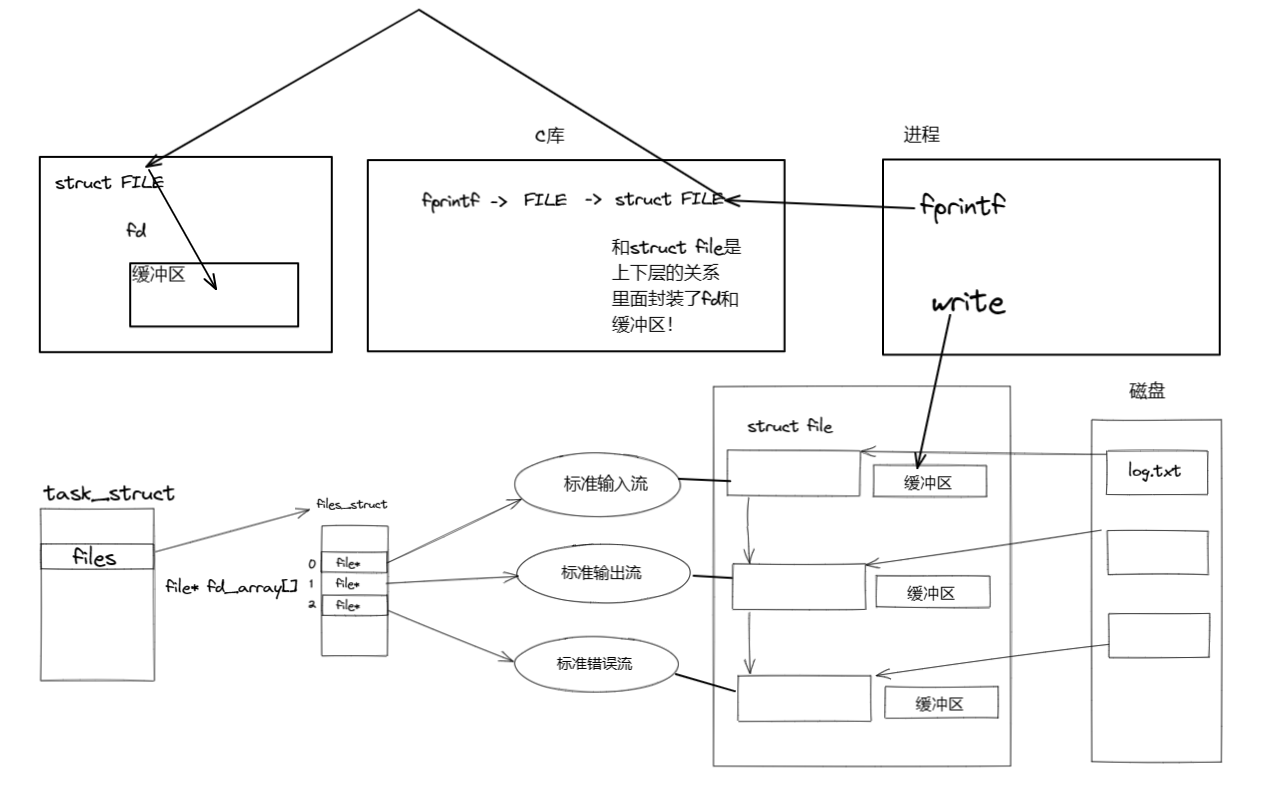
【LINUX】初识文件系统
文章目录一、前言二、回顾C语言文件操作三、初识系统调用openreadwriteclose四、文件系统初识五、结语一、前言 二、回顾C语言文件操作 int main() {FILE* fp fopen("log.txt", "w");if (fp NULL){perror("fopen");}int cnt 0;fputs("…...

金三银四Java面试题及答案整理(2023最新版) 持续更新
作为一名优秀的程序员,技术面试是不可避免的一个环节,一般技术面试官都会通过自己的方式去考察程序员的技术功底与基础理论知识。 如果你参加过一些大厂面试,肯定会遇到一些这样的问题: 1、看你项目都用的框架,熟悉 …...

7个角度,用 ChatGPT 玩转机器学习
大家好,我是机器学习科普创作者章北海mlpy,探索更高效的学习方法是我一直等追求。现在的初学者太幸福了,可以利用ChatGPT来帮助你学习机器学习的各个方面。 比如【个人首测】百度文心一言 VS GPT-4这篇文章中,我就用文心一言、GP…...
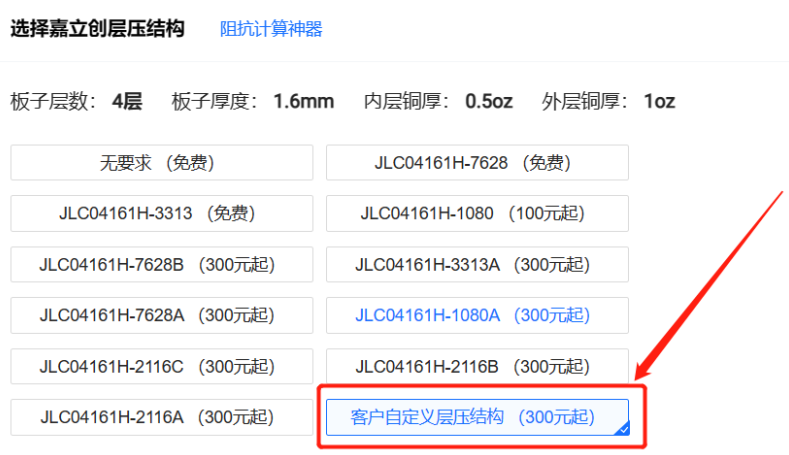
关于多层板,你了解多少?
01 前言 大家好,我是张巧龙。好久没写原创了,记得之前刚接触PCB时,还在用腐蚀单层板,类似这种。 慢慢随着电子产品功能越来越多,产品越来越薄,对PCB设计要求越来越高了,复杂程度也随之增加。因此…...

使用sqlalchemy-gbasedbt连接GBase 8s数据库
测试环境: 操作系统:CentOS 7.9 64-bit数据库版本:GBase8sV8.8_AEE_3.0.0_1,对应的CSDK版本为3.0.0_1 1,确认安装python3 确认已经安装python3和python3-devel [rootlocalhost test]# python3 -V Python 3.6.8如果…...

前端如何丢掉你的饭碗?
对于后端而言,我们常有“删库跑路”的说法,这说明后端的操作对于信息系统而言通常影响很大,可以轻易使信息系统宕机、崩溃,直接导致项目失败。所以,不要去逼后端程序员! 作为前端程序员,我们似…...
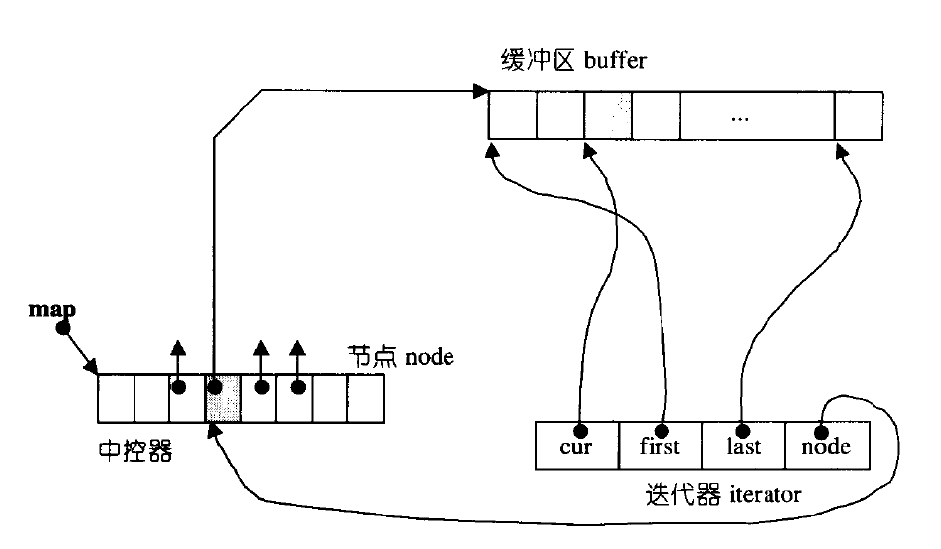
栈、队列、优先级队列的模拟实现
优先级队列的模拟实现栈stack的模拟实现push()pop()top()size()empty()swap()stack总代码队列queue的模拟实现push()pop()front()back()empty()size()swap()queue总代码优先级队列(堆)push()pop()top()empty()size()swap()priority_queue总代码deque的了解栈 在CSTL中栈并不属…...
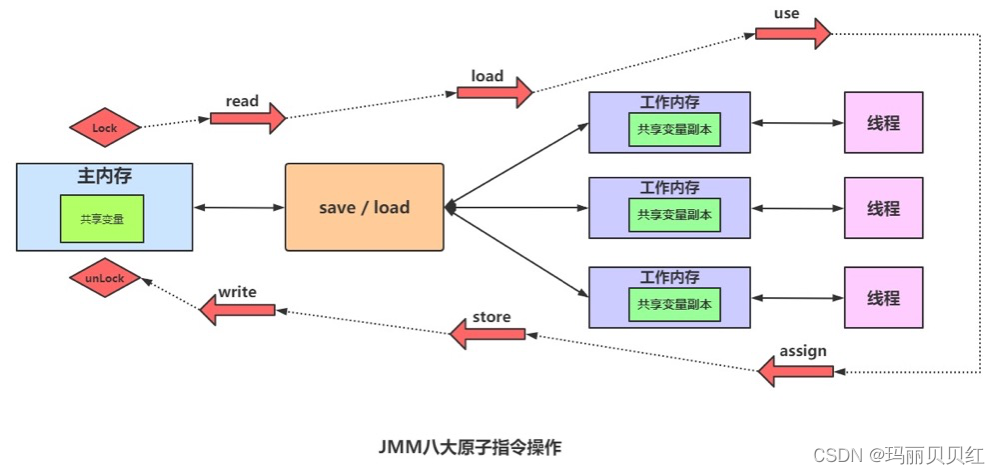
JMM内存模型
JMM内存模型JMM内存模型定义三大特性原子性可见性有序性volatile语义JMM规则操作系统实现术语缓存一致性要求缓存一致性机制写传播事务串行化重排序as-if-serial 语义(像是有序的)happens-before 原则happens-before 原则的八大子原则内存屏障总结finalf…...

Linux- 系统随你玩之--玩出花活的命令浏览器-双生姐妹花
文章目录1、背景2、命令浏览器-双生姐妹花2.1、姐妹花简介2.2 、验名正身2.3、常用功能选项3、常用实操3.1、发送请求获取文件3.1.1、抓取页面内容到一个文件中3.1.2、多个文件下载3.1.3、下载ftp文件3.1.4、断点续传3.1.5、上传文件3.1.6、内容输出3.2 、利用curl测试接口3.3 …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
